Курсовая работа: Airfoils and Lift
Курсовая работа: Airfoils and Lift
Airfoils
and Lift
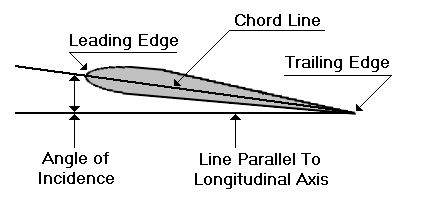
The angle
of incidence is measured by the angle at which the wing is attached to the
fuselage.
An airfoil is
a device which gets a useful reaction from air moving over its surface. When an
airfoil is moved through the air, it is capable of producing lift. Wings,
horizontal tail surfaces, vertical tails surfaces, and propellers are all
examples of airfoils.
Generally the
wing of small aircraft will look like the cross-section of the figure above.
The forward part of an airfoil is rounded and is called the leading edge. The
aft part is narrow and tapered and is called the trailing edge. A reference
line often used in discussing airfoils is the chord, an imaginary straight line
joining the extremities of the leading and trailing edges.
Angle of
Incidence: The angle of incidence is the angle formed by the longitudinal axis of
the airplane and the chord of the wing. The longitudinal axis is an imaginary
line that extends lengthwise through the fuselage from nose to tail. The angle
of incidence is measured by the angle at which the wing is attached to the
fuselage. The angle of incidence is fixed --it normally cannot be changed by
the pilot. (An exception
is the Vought F8U Crusader.)
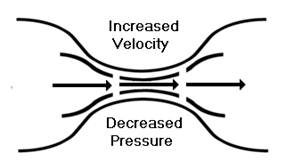
Bernoulli's
Principle: To understand how lift is produced, we must examine a phenomenon
discovered many years ago by the scientist Bernoulli and later called
Bernoulli's Principle: The pressure of a fluid (liquid or gas) decreases at
points where the speed of the fluid increases. In other words, Bernoulli found
that within the same fluid, in this case air, high speed flow is associated with
low pressure, and low speed flow with high pressure. This principle was first
used to explain changes in the pressure of fluid flowing within a pipe whose
cross-sectional area varied. In the wide section of the gradually narrowing
pipe, the fluid moves at low speed, producing high pressure. As the pipe
narrows it must contain the same amount of fluid. In this narrow section, the
fluid moves at high speed, producing low pressure.
An
important application of this phenomenon is made in giving lift to the wing of
an airplane, an airfoil. The airfoil is designed to increase the velocity of
the airflow above its surface, thereby decreasing pressure above the airfoil.
Simultaneously, the impact of the air on the lower surface of the airfoil
increases the pressure below. This combination of pressure decrease above and
increase below produces lift.
Lift:
Probably
you have held your flattened hand out of the window of a moving automobile. As
you inclined your hand to the wind, the force of air pushed against it forcing
your hand to rise. The airfoil (in this case, your hand) was deflecting the
wind which, in turn, created an equal and opposite dynamic pressure on the
lower surface of the airfoil, forcing it up and back. The upward component of
this force is lift; the backward component is drag.
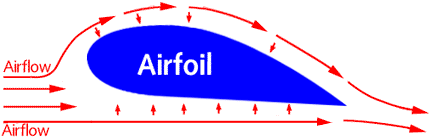
Pressure
is reduced is due to the smaller space the air has above the wing than below.
Air cannot go through the wing, so it must push around it. The surface air
molecules push between the wing and outer layers of air. Due to the bump of the
airfoil, the space is smaller and the molecules must go faster. According to Bernoulli's
Law, faster air has lower air pressure, and thus the high pressure beneath the
wing pushes up to cause lift.
How
Airplanes Fly: A Physical Description of Lift c
David Anderson
Fermi National
Accelerator Laboratory
Batavia IL
60510
dfa@fnal.gov
&
Scott Eberhardt
Dept. of
Aeronautics and Astronautics
University of
Washington
Seattle WA
91895-2400
scott@aa.washington.edu
Almost
everyone today has flown in an airplane. Many ask the simple question
"what makes an airplane fly"? The answer one frequently gets is
misleading and often just plain wrong. We hope that the answers provided here
will clarify many misconceptions about lift and that you will adopt our
explanation when explaining lift to others. We are going to show you that lift
is easier to understand if one starts with Newton rather than Bernoulli. We
will also show you that the popular explanation that most of us were taught is
misleading at best and that lift is due to the wing diverting air down.
Let
us start by defining three descriptions of lift commonly used in textbooks and
training manuals. The first we will call the Mathematical Aerodynamics
Description which is used by aeronautical engineers. This description uses
complex mathematics and/or computer simulations to calculate the lift of a
wing. These are design tools which are powerful for computing lift but do not
lend themselves to an intuitive understanding of flight.
The
second description we will call the Popular Explanation which is based on the
Bernoulli principle. The primary advantage of this description is that it is
easy to understand and has been taught for many years. Because of its
simplicity, it is used to describe lift in most flight training manuals. The
major disadvantage is that it relies on the "principle of equal transit
times" which is wrong. This description focuses on the shape of the wing
and prevents one from understanding such important phenomena as inverted
flight, power, ground effect, and the dependence of lift on the angle of attack
of the wing.
The
third description, which we are advocating here, we will call the Physical
Description of lift. This description is based primarily on Newton’s laws. The
physical description is useful for understanding flight, and is accessible to
all who are curious. Little math is needed to yield an estimate of many
phenomena associated with flight. This description gives a clear, intuitive
understanding of such phenomena as the power curve, ground effect, and
high-speed stalls. However, unlike the mathematical aerodynamics description,
the physical description has no design or simulation capabilities.
The popular explanation of lift
Students of
physics and aerodynamics are taught that airplanes fly as a result of
Bernoulli’s principle, which says that if air speeds up the pressure is
lowered. Thus a wing generates lift because the air goes faster over the top
creating a region of low pressure, and thus lift. This explanation usually
satisfies the curious and few challenge the conclusions. Some may wonder why
the air goes faster over the top of the wing and this is where the popular
explanation of lift falls apart.
In
order to explain why the air goes faster over the top of the wing, many have
resorted to the geometric argument that the distance the air must travel is
directly related to its speed. The usual claim is that when the air separates
at the leading edge, the part that goes over the top must converge at the
trailing edge with the part that goes under the bottom. This is the so-called
"principle of equal transit times".
As
discussed by Gail Craig (Stop Abusing Bernoulli! How Airplanes Really Fly,
Regenerative Press, Anderson, Indiana, 1997), let us assume that this argument
were true. The average speeds of the air over and under the wing are easily
determined because we can measure the distances and thus the speeds can be
calculated. From Bernoulli’s principle, we can then determine the pressure
forces and thus lift. If we do a simple calculation we would find that in order
to generate the required lift for a typical small airplane, the distance over
the top of the wing must be about 50% longer than under the bottom. Figure 1
shows what such an airfoil would look like. Now, imagine what a Boeing 747 wing
would have to look like!

Fig
1 Shape of wing predicted by principle of equal transit time.
If
we look at the wing of a typical small plane, which has a top surface that is
1.5 - 2.5% longer than the bottom, we discover that a Cessna 172 would have to
fly at over 400 mph to generate enough lift. Clearly, something in this
description of lift is flawed.
But,
who says the separated air must meet at the trailing edge at the same time?
Figure 2 shows the airflow over a wing in a simulated wind tunnel. In the
simulation, colored smoke is introduced periodically. One can see that the air
that goes over the top of the wing gets to the trailing edge considerably
before the air that goes under the wing. In fact, close inspection shows that
the air going under the wing is slowed down from the "free-stream"
velocity of the air. So
much for the principle of equal transit times.
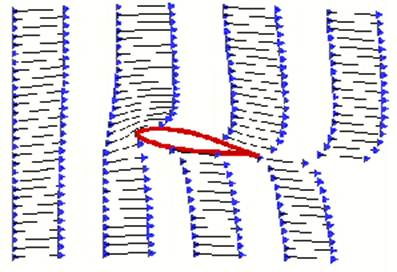
Fig
2 Simulation of the airflow over a wing in a wind tunnel, with colored "smoke"
to show the acceleration and deceleration of the air.
The
popular explanation also implies that inverted flight is impossible. It
certainly does not address acrobatic airplanes, with symmetric wings (the top
and bottom surfaces are the same shape), or how a wing adjusts for the great
changes in load such as when pulling out of a dive or in a steep turn.
So,
why has the popular explanation prevailed for so long? One answer is that the
Bernoulli principle is easy to understand. There is nothing wrong with the
Bernoulli principle, or with the statement that the air goes faster over the
top of the wing. But, as the above discussion suggests, our understanding is
not complete with this explanation. The problem is that we are missing a vital
piece when we apply Bernoulli’s principle. We can calculate the pressures
around the wing if we know the speed of the air over and under the wing, but
how do we determine the speed?
Another
fundamental shortcoming of the popular explanation is that it ignores the work
that is done. Lift requires power (which is work per time). As will be seen
later, an understanding of power is key to the understanding of many of the
interesting phenomena of lift.
Newton’s laws and lift
So, how does a
wing generate lift? To begin to understand lift we must return to high school
physics and review Newton’s first and third laws. (We will introduce Newton’s
second law a little later.) Newton’s first law states a body at rest will
remain at rest, and a body in motion will continue in straight-line motion
unless subjected to an external applied force. That means, if one sees a
bend in the flow of air, or if air originally at rest is accelerated into
motion, there is a force acting on it. Newton’s third law states that for
every action there is an equal and opposite reaction. As an example, an
object sitting on a table exerts a force on the table (its weight) and the
table puts an equal and opposite force on the object to hold it up. In order to
generate lift a wing must do something to the air. What the wing does to the
air is the action while lift is the reaction.
Let’s
compare two figures used to show streams of air (streamlines) over a wing. In
figure 3 the air comes straight at the wing, bends around it, and then leaves
straight behind the wing. We have all seen similar pictures, even in flight
manuals. But, the air leaves the wing exactly as it appeared ahead of the wing.
There is no net action on the air so there can be no lift! Figure 4 shows the
streamlines, as they should be drawn. The air passes over the wing and is bent
down. The bending of the air is the action. The reaction is the lift on the
wing.

Fig
3 Common depiction of airflow over a wing. This wing has no lift.
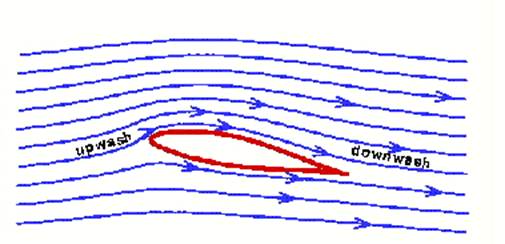
Fig
4 True airflow over a wing with lift, showing upwash and downwash.
The wing as a pump
As Newton’s
laws suggest, the wing must change something of the air to get lift. Changes in
the air’s momentum will result in forces on the wing. To generate lift a wing
must divert air down, lots of air.
The
lift of a wing is equal to the change in momentum of the air it diverts down.
Momentum is the product of mass and velocity. The lift of a wing is
proportional to the amount of air diverted down times the downward velocity of
that air. Its that simple. (Here we have used an alternate form of Newton’s
second law that relates the acceleration of an object to its mass and to the
force on it, F=ma) For more lift the wing can either divert more air (mass) or
increase its downward velocity. This downward velocity behind the wing is
called "downwash". Figure 5 shows how the downwash appears to the
pilot (or in a wind tunnel). The figure also shows how the downwash appears to
an observer on the ground watching the wing go by. To the pilot the air is
coming off the wing at roughly the angle of attack. To the observer on the
ground, if he or she could see the air, it would be coming off the wing almost
vertically. The greater the angle of attack, the greater the vertical velocity.
Likewise, for the same angle of attack, the greater the speed of the wing the
greater the vertical velocity. Both the increase in the speed and the increase
of the angle of attack increase the length of the vertical arrow. It is this
vertical velocity that gives the wing lift.
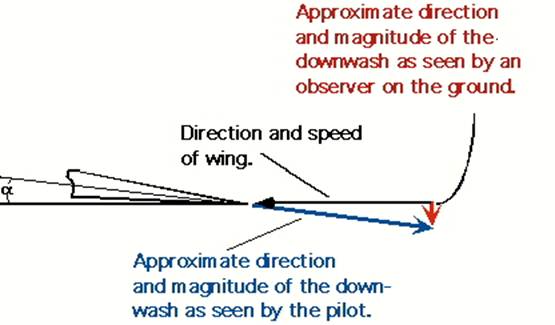
Fig
5 How downwash appears to a pilot and to an observer on the ground.
As
stated, an observer on the ground would see the air going almost straight down
behind the plane. This can be demonstrated by observing the tight column of air
behind a propeller, a household fan, or under the rotors of a helicopter, all
of which are rotating wings. If the air were coming off the blades at an angle
the air would produce a cone rather than a tight column. If a plane were to fly
over a very large scale, the scale would register the weight of the plane.
If
we estimate the average vertical component of the downwash of a Cessna 172
traveling at 110 knots to be about 9 knots, then to generate the needed 2,300
lbs of lift the wing pumps a whopping 2.5 ton/sec of air! In fact, as will be
discussed later, this estimate may be as much as a factor of two too low. The
amount of air pumped down for a Boeing 747 to create lift for its roughly
800,000 pounds takeoff weight is incredible indeed.
Pumping,
or diverting, so much air down is a strong argument against lift being just a
surface effect as implied by the popular explanation. In fact, in order to pump
2.5 ton/sec the wing of the Cessna 172 must accelerate all of the air within 9
feet above the wing. (Air weighs about 2 pounds per cubic yard at sea level.)
Figure 6 illustrates the effect of the air being diverted down from a wing. A
huge hole is punched through the fog by the downwash from the airplane that has
just flown over it.
So
how does a thin wing divert so much air? When the air is bent around the top of
the wing, it pulls on the air above it accelerating that air down, otherwise
there would be voids in the air left above the wing. Air is pulled from above
to prevent voids. This pulling causes the pressure to become lower above the
wing. It is the acceleration of the air above the wing in the downward
direction that gives lift. (Why the wing bends the air with enough force to
generate lift will be discussed in the next section.)
As
seen in figure 4, a complication in the picture of a wing is the effect of
"upwash" at the leading edge of the wing. As the wing moves along,
air is not only diverted down at the rear of the wing, but air is pulled up at
the leading edge. This upwash actually contributes to negative lift and more
air must be diverted down to compensate for it. This will be discussed later
when we consider ground effect.
Normally,
one looks at the air flowing over the wing in the frame of reference of the
wing. In other words, to the pilot the air is moving and the wing is standing
still. We have already stated that an observer on the ground would see the air
coming off the wing almost vertically. But what is the air doing above and
below the wing? Figure 7 shows an instantaneous snapshot of how air molecules are
moving as a wing passes by. Remember in this figure the air is initially at
rest and it is the wing moving. Ahead of the leading edge, air is moving up
(upwash). At the trailing edge, air is diverted down (downwash). Over the top
the air is accelerated towards the trailing edge. Underneath, the air is
accelerated forward slightly, if at all.
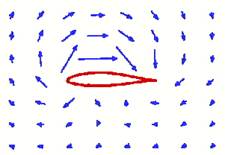
Fig
7 Direction of air movement around a wing as seen by an observer on the ground.
In
the mathematical aerodynamics description of lift this rotation of the air
around the wing gives rise to the "bound vortex" or
"circulation" model. The advent of this model, and the complicated
mathematical manipulations associated with it, leads to the direct
understanding of forces on a wing. But, the mathematics required typically
takes students in aerodynamics some time to master.
One
observation that can be made from figure 7 is that the top surface of the wing
does much more to move the air than the bottom. So the top is the more critical
surface. Thus, airplanes can carry external stores, such as drop tanks, under
the wings but not on top where they would interfere with lift. That is also why
wing struts under the wing are common but struts on the top of the wing have
been historically rare. A strut, or any obstruction, on the top of the wing
would interfere with the lift.
Air has viscosity
The natural
question is "how does the wing divert the air down?" When a moving
fluid, such as air or water, comes into contact with a curved surface it will
try to follow that surface. To demonstrate this effect, hold a water glass
horizontally under a faucet such that a small stream of water just touches the
side of the glass. Instead of flowing straight down, the presence of the glass
causes the water to wrap around the glass as is shown in figure 8. This
tendency of fluids to follow a curved surface is known as the Coanda effect.
From Newton’s first law we know that for the fluid to bend there must be a force
acting on it. From Newton’s third law we know that the fluid must put an equal
and opposite force on the object that caused the fluid to bend.
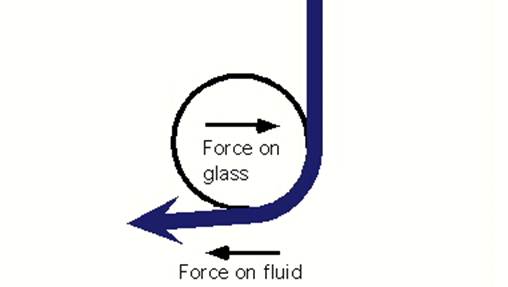
Fig
8 Coanda effect.
Why
should a fluid follow a curved surface? The answer is viscosity: the resistance
to flow which also gives the air a kind of "stickiness." Viscosity in
air is very small but it is enough for the air molecules to want to stick to
the surface. The relative velocity between the surface and the nearest air
molecules is exactly zero. (That is why one cannot hose the dust off of a car
and why there is dust on the backside of the fans in a wind tunnel.) Just above
the surface the fluid has some small velocity. The farther one goes from the
surface the faster the fluid is moving until the external velocity is reached
(note that this occurs in less than an inch). Because the fluid near the
surface has a change in velocity, the fluid flow is bent towards the surface.
Unless the bend is too tight, the fluid will follow the surface. This volume of
air around the wing that appears to be partially stuck to the wing is called
the "boundary layer".
Lift as a function of angle of attack
There are many
types of wing: conventional, symmetric, conventional in inverted flight, the
early biplane wings that looked like warped boards, and even the proverbial
"barn door." In all cases, the wing is forcing the air down, or more
accurately pulling air down from above. What all of these wings have in common
is an angle of attack with respect to the oncoming air. It is this angle of
attack that is the primary parameter in determining lift. The lift of the
inverted wing can be explained by its angle of attack, despite the apparent
contradiction with the popular explanation involving the Bernoulli principle. A
pilot adjusts the angle of attack to adjust the lift for the speed and load.
The popular explanation of lift which focuses on the shape of the wing gives
the pilot only the speed to adjust.
To
better understand the role of the angle of attack it is useful to introduce an
"effective" angle of attack, defined such that the angle of the wing
to the oncoming air that gives zero lift is defined to be zero degrees. If one
then changes the angle of attack both up and down one finds that the lift is
proportional to the angle. Figure 9 shows the coefficient of lift (lift
normalized for the size of the wing) for a typical wing as a function of the
effective angle of attack. A similar lift versus angle of attack relationship
is found for all wings, independent of their design. This is true for the wing
of a 747 or a barn door. The role of the angle of attack is more important than
the details of the airfoil’s shape in understanding lift.

Fig
9 Coefficient of lift versus the effective angle of attack.
Typically,
the lift begins to decrease at an angle of attack of about 15 degrees. The
forces necessary to bend the air to such a steep angle are greater than the
viscosity of the air will support, and the air begins to separate from the
wing. This separation of the airflow from the top of the wing is a stall.
The wing as air "scoop"
We now would
like to introduce a new mental image of a wing. One is used to thinking of a
wing as a thin blade that slices though the air and develops lift somewhat by
magic. The new image that we would like you to adopt is that of the wing as a
scoop diverting a certain amount of air from the horizontal to roughly the
angle of attack, as depicted in figure 10. The scoop can be pictured as an
invisible structure put on the wing at the factory. The length of the scoop is
equal to the length of the wing and the height is somewhat related to the chord
length (distance from the leading edge of the wing to the trailing edge). The
amount of air intercepted by this scoop is proportional to the speed of the
plane and the density of the air, and nothing else.
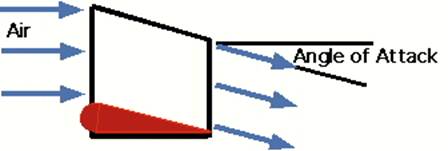
Fig
10 The wing as a scoop.
As
stated before, the lift of a wing is proportional to the amount of air diverted
down times the vertical velocity of that air. As a plane increases speed, the
scoop diverts more air. Since the load on the wing, which is the weight of the
plane, does not increase the vertical speed of the diverted air must be
decreased proportionately. Thus, the angle of attack is reduced to maintain a
constant lift. When the plane goes higher, the air becomes less dense so the
scoop diverts less air for the same speed. Thus, to compensate the angle of
attack must be increased. The concepts of this section will be used to
understand lift in a way not possible with the popular explanation.
Lift requires power
When a plane
passes overhead the formerly still air ends up with a downward velocity. Thus,
the air is left in motion after the plane leaves. The air has been given
energy. Power is energy, or work, per time. So, lift must require power. This
power is supplied by the airplane’s engine (or by gravity and thermals for a
sailplane).
How
much power will we need to fly? The power needed for lift is the work (energy)
per unit time and so is proportional to the amount of air diverted down times
the velocity squared of that diverted air. We have already stated that the lift
of a wing is proportional to the amount of air diverted down times the downward
velocity of that air. Thus, the power needed to lift the airplane is
proportional to the load (or weight) times the vertical velocity of the air.
If the speed of the plane is doubled the amount of air diverted down doubles.
Thus the angle of attack must be reduced to give a vertical velocity that is
half the original to give the same lift. The power required for lift has been
cut in half. This shows that the power required for lift becomes less as the
airplane's speed increases. In fact, we have shown that this power to create
lift is proportional to one over the speed of the plane.
But,
we all know that to go faster (in cruise) we must apply more power. So there
must be more to power than the power required for lift. The power associated
with lift, described above, is often called the "induced" power.
Power is also needed to overcome what is called "parasitic" drag,
which is the drag associated with moving the wheels, struts, antenna, etc.
through the air. The energy the airplane imparts to an air molecule on impact
is proportional to the speed squared. The number of molecules struck per time
is proportional to the speed. Thus the parasitic power required to overcome
parasitic drag increases as the speed cubed.
Figure
11 shows the power curves for induced power, parasitic power, and total power
which is the sum of induced power and parasitic power. Again, the induced power
goes as one over the speed and the parasitic power goes as the speed cubed. At
low speed the power requirements of flight are dominated by the induced power.
The slower one flies the less air is diverted and thus the angle of attack must
be increased to maintain lift. Pilots practice flying on the "backside of
the power curve" so that they recognize that the angle of attack and the
power required to stay in the air at very low speeds are considerable.
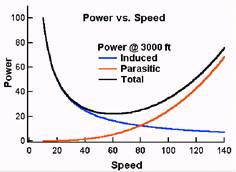
Fig
11 Power requirements versus speed.
At
cruise, the power requirement is dominated by parasitic power. Since this goes
as the speed cubed an increase in engine size gives one a faster rate of climb
but does little to improve the cruise speed of the plane.
Since
we now know how the power requirements vary with speed, we can understand drag,
which is a force. Drag is simply power divided by speed. Figure 12 shows the
induced, parasitic, and total drag as a function of speed. Here the induced
drag varies as one over speed squared and parasitic drag varies as the speed
squared. Taking a look at these curves one can deduce a few things about how
airplanes are designed. Slower airplanes, such as gliders, are designed to
minimize induced drag (or induced power), which dominates at lower speeds. Faster
airplanes are more concerned with parasitic drag (or parasitic power).
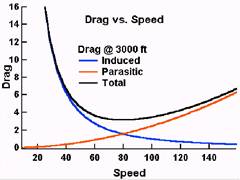
Fig
12 Drag versus speed.
Wing efficiency
At cruise, a
non-negligible amount of the drag of a modern wing is induced drag. Parasitic
drag, which dominates at cruise, of a Boeing 747 wing is only equivalent to
that of a 1/2-inch cable of the same length. One might ask what affects the
efficiency of a wing. We saw that the induced power of a wing is proportional
to the vertical velocity of the air. If the length of a wing were to be
doubled, the size of our scoop would also double, diverting twice as much air.
So, for the same lift the vertical velocity (and thus the angle of attack)
would have to be halved. Since the induced power is proportional to the
vertical velocity of the air, it too is reduced by half. Thus, the lifting
efficiency of a wing is proportional to one over the length of the wing. The
longer the wing the less induced power required to produce the same lift,
though this is achieved with an increase in parasitic drag. Low speed airplanes
are affected more by induced drag than fast airplanes and so have longer wings.
That is why sailplanes, which fly at low speeds, have such long wings.
High-speed fighters, on the other hand, feel the effects of parasitic drag more
than our low speed trainers. Therefore, fast airplanes have shorter wings to
lower parasite drag.
There
is a misconception held by some that lift does not require power. This comes
from aeronautics in the study of the idealized theory of wing sections
(airfoils). When dealing with an airfoil, the picture is actually that of a
wing with infinite span. Since we have seen that the power necessary for lift
is proportional to one over the length of the wing, a wing of infinite span
does not require power for lift. If lift did not require power airplanes would
have the same range full as they do empty, and helicopters could hover at any
altitude and load. Best of all, propellers (which are rotating wings) would not
require power to produce thrust. Unfortunately, we live in the real world where
both lift and propulsion require power.
Power and wing loading
Let us now
consider the relationship between wing loading and power. Does it take more
power to fly more passengers and cargo? And, does loading affect stall speed?
At a constant speed, if the wing loading is increased the vertical velocity
must be increased to compensate. This is done by increasing the angle of
attack. If the total weight of the airplane were doubled (say, in a 2-g turn)
the vertical velocity of the air is doubled to compensate for the increased
wing loading. The induced power is proportional to the load times the vertical
velocity of the diverted air, which have both doubled. Thus the induced power
requirement has increased by a factor of four! The same thing would be true if
the airplane’s weight were doubled by adding more fuel, etc.
One
way to measure the total power is to look at the rate of fuel consumption.
Figure 13 shows the fuel consumption versus gross weight for a large transport
airplane traveling at a constant speed (obtained from actual data). Since the
speed is constant the change in fuel consumption is due to the change in
induced power. The data are fitted by a constant (parasitic power) and a term
that goes as the load squared. This second term is just what was predicted in
our Newtonian discussion of the effect of load on induced power.
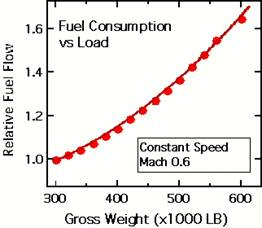
Fig
13 Fuel consumption versus load for a large transport airplane traveling at a
constant speed.
The
increase in the angle of attack with increased load has a downside other than
just the need for more power. As shown in figure 9 a wing will eventually stall
when the air can no longer follow the upper surface, that is, when the critical
angle is reached. Figure 14 shows the angle of attack as a function of airspeed
for a fixed load and for a 2-g turn. The angle of attack at which the plane
stalls is constant and is not a function of wing loading. The stall speed
increases as the square root of the load. Thus, increasing the load in a 2-g
turn increases the speed at which the wing will stall by 40%. An increase in
altitude will further increase the angle of attack in a 2-g turn. This is why
pilots practice "accelerated stalls" which illustrate that an
airplane can stall at any speed. For any speed there is a load that will induce
a stall.
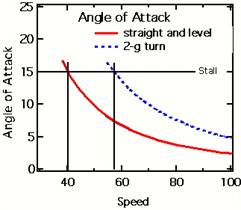
Fig
14 Angle of attack versus speed for straight and level flight and for a 2-g
turn.
Wing vortices
One might ask
what the downwash from a wing looks like. The downwash comes off the wing as a
sheet and is related to the details of the load distribution on the wing.
Figure 15 shows, through condensation, the distribution of lift on an airplane
during a high-g maneuver. From the figure one can see that the distribution of
load changes from the root of the wing to the tip. Thus, the amount of air in
the downwash must also change along the wing. The wing near the root is
"scooping" up much more air than the tip. Since the root is diverting
so much air the net effect is that the downwash sheet will begin to curl outward
around itself, just as the air bends around the top of the wing because of the
change in the velocity of the air. This is the wing vortex. The tightness of
the curling of the wing vortex is proportional to the rate of change in lift
along the wing. At the wing tip the lift must rapidly become zero causing the
tightest curl. This is the wing tip vortex and is just a small (though often
most visible) part of the wing vortex. Returning to figure 6 one can clearly
see the development of the wing vortices in the downwash as well as the wing
tip vortices.

Fig
15 Condensation showing the distribution of lift along a wing. The wingtip
vortices are also seen. (from Patterns in the Sky, J.F. Campbell and J.R.
Chambers, NASA SP-514.)
Winglets
(those small vertical extensions on the tips of some wings) are used to improve
the efficiency of the wing by increasing the effective length of the wing. The
lift of a normal wing must go to zero at the tip because the bottom and the top
communicate around the end. The winglets blocks this communication so the lift
can extend farther out on the wing. Since the efficiency of a wing increases
with length, this gives increased efficiency. One caveat is that winglet design
is tricky and winglets can actually be detrimental if not properly designed.
Ground effect
Another common
phenomenon that is misunderstood is that of ground effect. That is the
increased efficiency of a wing when flying within a wing length of the ground.
A low-wing airplane will experience a reduction in drag by 50% just before it
touches down. There is a great deal of confusion about ground effect. Many
pilots (and the FAA VFR Exam-O-Gram No. 47) mistakenly believe that ground
effect is the result of air being compressed between the wing and the ground.
To
understand ground effect it is necessary to have an understanding of upwash.
For the pressures involved in low speed flight, air is considered to be
non-compressible. When the air is accelerated over the top of the wing and
down, it must be replaced. So some air must shift around the wing (below and
forward, and then up) to compensate, similar to the flow of water around a
canoe paddle when rowing. This is the cause of upwash.
As
stated earlier, upwash is accelerating air in the wrong direction for lift.
Thus a greater amount of downwash is necessary to compensate for the upwash as
well as to provide the necessary lift. Thus more work is done and more power
required. Near the ground the upwash is reduced because the ground inhibits the
circulation of the air under the wing. So less downwash is necessary to provide
the lift. The angle of attack is reduced and so is the induced power, making
the wing more efficient.
Earlier,
we estimated that a Cessna 172 flying at 110 knots must divert about 2.5
ton/sec to provide lift. In our calculations we neglected the upwash. From the
magnitude of ground effect, it is clear that the amount of air diverted is
probably more like 5 ton/sec.
Conclusions
Let us review
what we have learned and get some idea of how the physical description has
given us a greater ability to understand flight. First what have we learned:
·
The
amount of air diverted by the wing is proportional to the speed of the wing and
the air density.
·
The
vertical velocity of the diverted air is proportional to the speed of the wing
and the angle of attack.
·
The
lift is proportional to the amount of air diverted times the vertical velocity
of the air.
·
The
power needed for lift is proportional to the lift times the vertical velocity
of the air.
Now let us
look at some situations from the physical point of view and from the
perspective of the popular explanation.
·
The
plane’s speed is reduced. The physical view says that the amount of air
diverted is reduced so the angle of attack is increased to compensate. The power
needed for lift is also increased. The popular explanation cannot address this.
·
The
load of the plane is increased. The physical view says that the amount of air
diverted is the same but the angle of attack must be increased to give
additional lift. The power needed for lift has also increased. Again, the
popular explanation cannot address this.
·
A
plane flies upside down. The physical view has no problem with this. The plane
adjusts the angle of attack of the inverted wing to give the desired lift. The popular explanation implies that
inverted flight is impossible.
As one can
see, the popular explanation, which fixates on the shape of the wing, may
satisfy many but it does not give one the tools to really understand flight.
The physical description of lift is easy to understand and much more powerful.
Axis
of Rotation
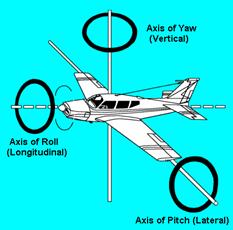
Axis of an
Airplane in Flight.
An airplane
may turn about three axes. Whenever the attitude of the airplane changes in
flight (with respect to the ground or other fixed object), it will rotate about
one or more of these axes. Think of these axes as imaginary axles around which
the airplane turns like a wheel. The three axes intersect at the center of
gravity and each one is perpendicular to the other two.
Longitudinal
Axis: The
imaginary line that extends lengthwise through the fuselage, from nose to tail,
is the longitudinal axis. Motion about the longitudinal axis is roll and is
produced by movement of the ailerons located at the trailing edges of the
wings.
Lateral
Axis: The
imaginary line which extends crosswise, wing tip to wing tip, is the lateral
axis. Motion about the lateral axis is pitch and is produced by movement of the
elevators at the rear of the horizontal tail assembly.
Vertical
Axis: The
imaginary line which passes vertically through the center of gravity is the vertical
axis. Motion about the vertical axis is yaw and is produced by movement of the
rudder located at the rear of the vertical tail assembly.
DETAILS
OF MODERN AIRSHIPS - 1927
Advantages
of Rigid Type Airships--Airship Frame Construction--Large Airships
Projected--Army Non-rigid Dirigibles--Requirements of Airships for Civilian
Flying.
Advantages
of Rigid Type Airship. Before describing typical lighter- than-air craft or airships
that have received actual commercial as well as military usage, it may be well
to briefly review some of the advantages of the rigid type, which is the one
that lends itself most easily to large structures and which is also the safest
of the three types we have previously reviewed in Chapter II which is devoted
to a consideration of the elementary principles underlying airship construction
and application. Rigid airships have made longer single flights than other
types and have flown more hours and miles without refueling than any other
form. The rigid airship is said to be the fastest large vehicle of
transportation that engineering ability of man has yet evolved. The Navy
Airship Los Angeles, shown near the mooring mast at Lakehurst, N. J. to which
it may be anchored is depicted at Fig. 315. A design of the new 6,500,000 cubic
foot capacity ship recently authorized by Congress is shown at Fig. 316 flying
over a battleship at an elevation of about 1,500 feet. The rigid airship, owing
to its large size and light weight can carry more load than any other type of
aircraft. It is independent of topography as oceans and continents are but
areas to fly over. Land vehicles must stop when they reach water, water
transport must stop when the ship is docked.
Airship
Frame Construction. The rigid airship, because of its bulkhead system, in which
the lifting gas is carried in 16 to 20 cells, has a much greater safety factor
than the types in which the gas is carried in only one or two containers. In
event of damage to one or two cells, the ship can continue its journey and
repairs can be made to a leaky gas cell while in flight.
The
rigid ship has a complete metal framework. Girders extend from nose to tail, or
in nautical parlance, from stem to stern. Ring girders set at intervals brace
the longitudinals and are themselves internally reinforced by cross girders and
tension wire bracing. The entire framework is enclosed by a network of wiring
and the whole is streamlined or faired to minimize air resistance with a fabric
covering.
The
view of the crew's quarters on the Bodensee, a German air liner at Fig. 317,
shows the triangular keel member with the cat-walk by which the crew can travel
from one end of the ship to the other and gain access to the different gas
bags. The character of the longitudinal duralumin girders and the way they are
braced by the ring girders is clearly shown at Fig. 318. This depicts that
portion of the hull where one set of fuel tanks are located. The view at Fig.
319 shows the interior with the deflated gas cells hanging from the top-most
longitudinal ready for inflation.
The
outer skin is in place and the large size and extreme lightness of the
structure is clearly shown. The passenger cabin of the Deutschland, another
rigid dirigible of the Zepellin series is shown at Fig. 320. Wicker chairs are
used because of their light weight and the interior structure of the cabin can
be determined by study of the illustration.
The
control of a Zepellin type airship is not as simple as that of an airplane and
no one man is at the controls. Special controls are provided for the elevators
and still another set for the vertical rudders. The elevator control of the L59
with the instruments for altitude navigation is shown at Fig. 321. Control is
by a large wheel similar to the steering wheel of a ship. Directional control
is by a similar wheel at another part of the control car.
Large
Airship Projected. The largest of the United States Navy airships, the
Shenandoah was 600 feet long with a capacity of 2,115,000 cubic feet. The
projected airship designed by the engineers of the Goodyear- Zepellin Company,
while it has over three times the capacity of the Shenandoah will be only 100
feet longer and will be of such size that it may be housed in the Lakehurst
hangar. The illustration at Fig. 322 shows how the new ships authorized by
congress will compare with the Shenandoah. The control car will be built into the
hull and streamlined. Engines of 4,800 horsepower, giving a speed of 90 miles
per hour with fuel for from 5,000 to 8,000 miles will drive the ship. The air
screws will be fitted in tilting mountings, which will turn in a 90 degree arc
to help force the ship upward or downward as desired and greatly aid in
controlling the huge vessel.
It
will embody the proved structural advantages of some 135 ships built in the
past.
(a)
Multiple gas cells which function like bulk-heading on a steamship, so that if
one or more cells fail the ship will still remain aloft: (b) The triple cover
system, one cover to hold the lifting gas, one consisting of the shape-forming
duralumin frame-work, and an outer cover to shed rain and snow, to reflect
rather than to absorb heat, and to present a fair surface; (c) invulnerability
against lightning; (d) accessibility to inspection and repair.
It
will however present certain new features as well of far reaching importance:
(a) A double or triple keel giving added longitudinal strength comparable to
the breaking strength of one length of metal, as against two or three bolted
together; (b) a new type of ring girder each internally braced and structurally
self sufficient, which (c) will permit the control car and even the power cars
to be built within the hull; (d) even fuller accessiblity to continuous
inspection and permitting repairs to be made even in flight; (e) the use of new
fuels to conserve helium and reduce weight.
Army Non-Rigid Dirigibles. The non-rigid dirigible is the smallest of the
three types as the largest now being built in the United States for the Army
and Navy service have a gas capacity of about one-tenth that of the Los
Angeles. Under ordinary conditions a 230,000 cubic foot non-rigid has a
cruising radius of from 500 to 1,000 miles and an air endurance of from 18 to
24 hours. Such airships are essentially motorized free balloons and the engines
are carried in a car attached to the lower side or bottom of the bag. The
Pilgrim, a small non-rigid previously described with a gas capacity of 50,000
cubic feet has a speed of 50 miles per hour and is propelled by a Wright
"Gale" three-cylinder engine as shown at Fig. 323. This small ship
was built to carry four passengers. The gas in non-rigid ships, as in the army
TC types, as shown at Fig. 324 is contained in a single bag, but an inner two
compartment bag, called the ballonet, is filled with air to keep the main
container properly distended because the air pressure can be made to compensate
for variations in gas pressure in the bag. These ships have a capacity of about
200,000 cubic feet, are 196 feet long overall and 47 feet in extreme height.
The hull diameter is 33.5 feet. The fineness ratio is 4.4 to 1. The total lift
is 11,584 pounds of which the useful lift is about 4,000 pounds. The gross
weight per horsepower is 38.6 pounds. Two Wright Type I water-cooled engines of
150 horsepower each were provided on the first ships of this series but these
have been replaced on later types with two Wright J1 engines, which are nine-cylinder
radial air-cooled types driving tractor propellers 9 feet 10 inches in
diameter. It is claimed that the saving of 400 pounds over the water-cooled
installation permits an increase of speed from 54 to 60 miles per hour; with an
increase in range of 10 per cent.
Flight
Control Surfaces - Elevons
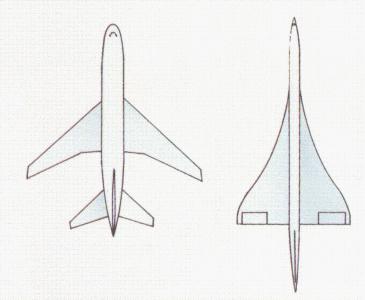
Delta
winged aircraft use elevons as primary flight controls for
roll and
pitch.
Elevon:
Delta
winged aircraft can not use conventional 3 axis flight control systems because
of their unique delta shape. Therefore, it uses a device called an elevon. It
is a combination of ailerons and elevators.
The
elevon is used as an aileron. Ailerons control motion along the longitudinal
axis. The longitudinal axis is an imaginary line that runs from the nose to the
tail. Motion about the longitudinal axis is called roll.
The
elevon is also used as an elevator. Elevators control motion along the lateral
axis. The lateral axis is an imaginary line that extends crosswise, from
wingtip to wingtip. Motion
about the lateral axis is called pitch.
| Fokker DR.I - Thoughts on Wing
Failures |
|
by Mike Tate
© 2000
|
|
The recent
WWI AERO article (#165, Aug, 1999) concerning wing failures in the Nieuport
28 prompted me to put some ideas to paper, regarding those more familiar
failures of the Fokker triplane.
The
reputation of Fokker aircraft for fragility was mainly the result of
structural problems with the Dr.I triplane and D.VIII cantilever monoplane.
The D.VIII wing problem was due to flexural failure (ie, they broke in
bending); and the evidence indicates that this was due to production
quality-control inadequacies rather than deficiencies of design or technical
understanding. The Dr.I, however, is a different "kettle of fish"
in that it experienced failures very like those of the Nieuport 28, namely
that of "wing stripping." Unlike the D.VIII, the triplane was
grounded not because of spar failure, but because of the disintegration of
the secondary structure- wing ribs etc- whilst the spars remained intact. The
similarity of the failures in the N28 and Dr.I is intriguing because the 2
aircraft are fundamentally different: one a biplane of almost sesquiplane
proportions, the other a triplane of equal-chord wings. The N28 had
thin-section wings, wire-braced; the Dr.I had thick sections and a cantilever
structure very different animals. For me, the most interesting fact of all
(and the most difficult to explain) has been that the failures always
occurred in the upper wings of either aircraft - to my knowledge there are no
reported incidents of failures in the lower planes.
In the case
of the 2 most notable triplane failures, the extent of the upper
wingstripping was almost total, with fatal consequences for Lieutenants
Gontermann and Pastor. It is of particular interest that, after the triplane
was reissued with modified wings, the same type of failure still occurred -
but to a more limited (and survivable) extent.
At the time
of the Dr.I grounding, after the 2 crashes mentioned, various theories were
proposed to account for the failures. Sand loading of the Fokker F5 (the Dr.I
prototype) had shown that the triplane cantilever wing cellule had excellent
strength for its period; and it fell to those interested to create new (and
unlikely) aerodynamic phenomena to account for the fatal discrepancy between
experiment and practice. Because the ailerons of both Gontermann's and
Pastor's aircraft were seen to detach, interest centered on the aileron
supporting-structure and related internal componentry.
Various
reinforcements were introduced, and emphasis was placed on better internal
protection of the glued structure by varnishing. (The peculiarity of upper
wing failures had not, of course, gone unnoticed at the time. The possibility
of the casein glue deteriorating, due to weathering, gave cause for concern -
the lower wings being considered to be somewhat protected - debatable, of
course.) Also poor workmanship was extensively uncovered in grounded aircraft
and Fokker was urged to improve on this aspect of his production of further
aircraft. However, as noted, failures continued to occur in the reissued
aircraft.
|
In the case of
the Nieuport 28, the fabric of the upper-wing top-surface together with the
entire leading edge would detach. On this aircraft, however, damage appears to
have been selflimiting at this point: the rib tails and undersurface, for
instance, always seem to have held up. This is just as well for the pilots
concerned, since the (almost) sesquiplane proportions of the N28 could not have
tolerated complete loss of the upper lifting area. Fortunately, the Nieuport
carried its ailerons on the lower plane so that roll control was available - no
doubt this helped survivability.
Of all WWI
aircraft, these 2 are the only ones I am aware of that suffered this type of
failure as a generic fault. "Ballooning" of wing fabric was a known
risk resulting from wing leading-edge damage. Wings failed simply through lack
of strength. Wings failed due to a lack of stiffness. (True sesquiplanes-
V-strutters, notably other Nieuport and Albatros models- are known to have
occasionally lost a lower plane due to a lack of torsional stiffness) - but
wingstripping seems mainly recorded for the 2 models in question. Since wing
reinforcement better weather protection and better-built quality did not fully
cure the triplane ills, then there was another factor at work. So what was it?
I began by
looking for a common factor. What is it that both aircraft possess which can
cause almost identical failure in a wing- and why only the top plane? There are
in fact, 2 unusual structural features present in both. Firstly, the main spars
are very closely spaced so that the rib noses project unusually far forward of
the spar group. The N28 spars are closely spaced, but maintain an orthodox
drag-bracing arrangement of steel tube and piano wire. The Dr.I located the
spars with a small separation, so that plywood closing-skins top and bottom
formed a single-spar system, accounting for both drag and to a limited extent,
torsion.
The other
critical feature present in both aircraft was the use of a plywood leading-edge
contour panel. This was relatively unusual in WWI. British aircraft seem not to
have used it at all, preferring intermediate riblets as leading-edge support;
and from a quick appraisal of my library, I have identified only 5 aircraft
which had this feature (I don't suppose this to be at a definitive.). These are
the Pfalz D.XII Fokkers Dr.I, D.VI and D.VII, and the Nieuport 28 (possibly
also the 27).
Some aircraft
wings were, of course, totally skinned in sheet plywood or aluminum; but with
these exceptions, at least, complete fabric cover was the norm. The use of
plywood leading-edge covering presents a problem in the attachment of fabric
since stringing (ie, the through-wing stitching normally used) would be
required to stop at the plywood-covered surface. This may account for the fact
that both the triplane and N28 are reported as originally having the fabric
tacked to the rib flanges rather than being sewn (which was considered to be
the correct way). The fabric attachment itself is therefore suspect but the
test still remains; why only failures of the upper wing? If the fabric
attachment was the critical factor, then failures could have occurred in any
wing with this feature, which would have included lower planes of both the
triplane and the N28.
Both aircraft
have structurally suspect features in their wing leading-edges. In the case of
the N28, the long rib-noses would produce large bending stresses (during
violent manoeuvres) at their main-spar attachment locations. Large bending
stresses can have attendant large shear stresses; and on the N28, these would
exist in the thin poplar rib-webs (typical of the period). This is a very risky
arrangement, since timber is not particularly strong when subject to shear
loading along the grain - plywood is much better. (The N28 rib-noses had very
little shear material anyway)
The other
suspect feature is that of the omission of rib-capping referred to in the
recent WWI AERO article. These details appear peculiar to the N28, and are at
the most extreme in the upper wing. There is little doubt that the upper wing
leading edge was simply of marginal strength; and at first sight it seems odd that
sandloading did not reveal this weakness. But of course this reveals a weakness
of sand-loading. The chordwise distribution of lift, at high angles of attack,
will not normally be represented by a heap of sand, since dry sand slumps to
approximately 45 deg- forming a triangular load distribution with a
centrally-located center of gravity. (This can be modified within limits by
constructing walls along the wing edges.) Sandloading therefore successfully
tests the wingspar adequacy, but is insufficient to the task of testing the rib
nose strength (and remember that here we have 2 aircraft which resolutely held
on to their spars, whilst liberally shedding secondary structure). This
proof-loading problem is exacerbated by the fact that wing lift (particularly
at large angles of attack) is largely generated by the negative pressure zone
existing on the forward upper surface (see Fig 18- taken from SIMPLE
AERODYNAMICS (1929), by Charles N Monteith.).
The critical
structural requirement under these loading conditions is to have adequate
"peel" strength between the upper skin and the substructure (ribs
and/or stringers etc). Both the N28 and the Dr.I were deficient here. The
Nieuport was devoid of rib cap-strips or spanwise stringers at the critical
location; the Dr.I leading-edge plywood was severely cut away at each rib, had
no supporting stringers, and had only minor connection to the main spar. With
this arrangement, a significant amount of the local lift- would have been
transmitted in a peel condition from the plywood skin to the supporting ribs -
there was no other load-path. Again, this is a very unreliable form of joint.
Today, the attachment of wing skins to substructure remains a critical factor;
in fact, where fuel is carried inside a wing much of the wing design is
overridingly determined by this consideration.
So, the
Nieuport had a weak upper-wing leading edge and larger chord to boot. This
could (as suggested in the WWI AERO article) be the complete answer to the N28
failures. But the Triplane had the same design condition on all wings, but only
the top wing ever failed. So there was something else.
It is not
common to see a biplane or triplane wing cellule in which equal-chord wings are
of differing span, although some famous aircraft such as the BE- 12, RE-8 and
Curtiss Jenny are exceptions. Typically, where an upper wing is of greater
span, it is often of greater chord also. This has the virtue of approximately
maintaining constant aspect-ratio for each wing in the complete wing system.
(To what extent this represented a design objective at the time I have no
information.)
The fact that
real wings are of finite span (as opposed to the theoretically infinite span
wing which is implicit in aerofoil section data) means that a real wing will
attain a particular lift coefficient at an angle of attack somewhat greater
than that apparent from he section-data. It also follows that wings of
differing aspect ratio, but identical section, will generate different
lift-intensities, to one another, when operating at the same angle of attack.
The Dr.1 had
aspect ratios of 6.8, 5.9 and 5.1 for the upper, middle and lower planes
respectively. The wing section (tested as the Gottingen 289 section after the war)
had a maximum lift coefficient of about 1.4. Making estimates for each of the
triplane wings (working as independent surfaces), the planes would require
19.2, 20 and 21 degrees respectively to reach the maximum lift coefficient.
When working at the same angle of attack (as in the aircraft alignment), the
upper wing would produce a lift intensity about 9% greater than the lower wing.
So could aspect-ratio be the cause of the Triplane wing failures? Well no, I am
afraid not. A 9% increased lift intensity cannot be considered sufficient to
always fail the upper wing before one or the other planes. Variations in
material strength and build quality would both have similar (or greater)
tolerance, which would occasionally bias the failure to one of the other planes.
There has to be something else – something more emphatic.
I found the
answer by chance, and I found it in a ‘history’ book. Whilst flipping through a
copy of SIMPLE AERODYNAMICS (1929), by Charles N Monteith, (Chief Engineer,
Boeing), looking for data on the Gottingen 289 section, I came across a
particularly relevant passage under Item 70, p89, “Pressure distribution tests
on MB-3A Airplane”, which is reproduced in facsimile here:
Paragraphs B
and C are telling. The loading distribution noted is very significant over the
biplane system described. A factor of 1.6 at high-lift coefficients cannot be
ignored. The Triplane system with its relatively smaller wing gaps and
pronounced stagger would almost certainly have a greater value than this.
Together with aspect-ratio effects it is not unreasonable to suggest that the
lift intensity of the upper wing of the Dr.I approached twice that of the
bottom wing. This is certainly enough to test the upper wing integrity before
the rest of the system.
Conclusion
I would
suggest that the Dr.I wing failures (and almost certainly those of the N28,
too) occurred because lift-grading (particularly), together with aspect-ratio
effects, caused the upper surface of the upper wing to be subject to much
greater lift intensity than the rest of the system. This tested a leading-edge
design of marginal strength, poorly made, to the point of collapse in
particular aircraft. The leading edge failure continued back across the wing
due to design details. Where rib tails, for example, were connected by a wire
trailing edge, ballooning fabric will exert tensile loading in this wire which
will then tend to "gather up" the rib tails and strip the wing. This
would also destabilize the area of the aileron support structures, and so on.
The strengthening of the wing aft of the spars and the improvements to build
quality, carried out after the original failures, would have acted to prevent
this catastrophic failure. But the root cause of the failure lift-grading) went
unappreciated until after the war when investigations like those at NACA were
conducted.
It would be
fascinating to know to what extent these factors were understood prior to 1918.
I expect that the concentration of lift forces (as an intense negative pressure
zone at the upper surface LE) was reasonably well appreciated by wind-tunnel
investigators- if only by the application of Bernoulli's theorem to the visible
flow patterns around test sections. Probably the effects of aspect ratio were
understood- even if only qualitatively; but lift-grading would require much
more complex investigation. Regarding the aspect-ratio issue; advocates of
multiplanes (Horatio Phillips, for example) appear to have worked from the
understanding that high aspect-ratio is a "good thing" (true) but not
to have had evidence of the detrimental effects of interference between
closely-spaced multi-plane wing systems.
But such is
the nature of progress - the testing of ideas. It took the lives of airmen to
drive the investigations which led to today's understanding of these matters
and which allow our complacent and sometimes arrogant review of history.
A final
thought. It is theoretically possible for the Fokker triplane to remain
airborne on its 2 lower planes alone (of 9.9 square metres area). The stall
speed would be about 64mph. No doubt, when both Gontermann and Pastor found
themselves in dire straits, they did the natural thing: to pull back on the
stick even though the aircraft was deeply stalled. Maybe if they had first pushed... ?
Forces Acting on an Airplane

The
airplane in straight-and-level unaccelerated flight is acted on by four forces.
The four forces are lift, gravity, thrust and drag.
The airplane
in straight-and-level unaccelerated flight is acted on by four forces--lift,
the upward acting force; weight, or gravity, the downward acting force; thrust,
the forward acting force; and drag, the backward acting, or retarding force of
wind resistance.
Lift
opposes gravity.
Thrust
opposes drag.
Drag and
weight are forces inherent in anything lifted from the earth and moved through
the air. Thrust and lift are artificially created forces used to overcome the
forces of nature and enable an airplane to fly. The engine and propeller
combination is designed to produce thrust to overcome drag. The wing is
designed to produce lift to overcome the weight (or gravity).
In
straight-and-level, unaccelerated flight, (Straight-and-level flight is
coordinated flight at a constant altitude and heading) lift equals weight and
thrust equals drag, though lift and weight will not equal thrust and drag. Any
inequality between lift and weight will result in the airplane entering a climb
or descent. Any inequality between thrust and drag while maintaining
straight-and-level flight will result in acceleration or deceleration until the
two forces become balanced.
Flight
Control Surfaces
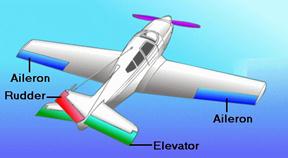
The three
primary flight controls are the ailerons, elevator and rudder.
Ailerons: The two ailerons, one at
the outer trailing edge of each wing, are movable surfaces that control
movement about the longitudinal axis. The movement is roll. Lowering the
aileron on one wing raises the aileron on the other. The wing with the lowered
aileron goes up because of its increased lift, and the wing with the raised
aileron goes down because of its decreased lift. Thus, the effect of moving
either aileron is aided by the simultaneous and opposite movement of the
aileron on the other wing.
Rods or cables
connect the ailerons to each other and to the control wheel (or stick) in the
cockpit. When pressure is applied to the right on the control wheel, the left
aileron goes down and the right aileron goes up, rolling the airplane to the
right. This happens because the down movement of the left aileron increases the
wing camber (curvature) and thus increases the angle of attack. The right
aileron moves upward and decreases the camber, resulting in a decreased angle
of attack. Thus, decreased lift on the right wing and increased lift on the
left wing cause a roll and bank to the right.
Elevators: The elevators control the
movement of the airplane about its lateral axis. This motion is pitch. The
elevators form the rear part of the horizontal tail assembly and are free to
swing up and down. They are hinged to a fixed surface--the horizontal
stabilizer. Together, the horizontal stabilizer and the elevators form a single
airfoil. A change in position of the elevators modifies the camber of the
airfoil, which increases or decreases lift.
Like the
ailerons, the elevators are connected to the control wheel (or stick) by
control cables. When forward pressure is applied on the wheel, the elevators
move downward. This increases the lift produced by the horizontal tail
surfaces. The increased lift forces the tail upward, causing the nose to drop.
Conversely, when back pressure is applied on the wheel, the elevators move
upward, decreasing the lift produced by the horizontal tail surfaces, or maybe
even producing a downward force. The tail is forced downward and the nose up.
The elevators
control the angle of attack of the wings. When back pressure is applied on the
control wheel, the tail lowers and the nose raises, increasing the angle of
attack. Conversely, when forward pressure is applied, the tail raises and the
nose lowers, decreasing the angle of attack.
Rudder: The rudder controls
movement of the airplane about its vertical axis. This motion is yaw. Like the
other primary control surfaces, the rudder is a movable surface hinged to a
fixed surface which, in this case, is the vertical stabilizer, or fin. Its
action is very much like that of the elevators, except that it swings in a
different plane--from side to side instead of up and down. Control cables
connect the rudder to the rudder pedals.
Trim Tabs: A trim tab is a small,
adjustable hinged surface on the trailing edge of the aileron, rudder, or elevator
control surfaces. Trim tabs are labor saving devices that enable the pilot to
release manual pressure on the primary controls.
Some airplanes
have trim tabs on all three control surfaces that are adjustable from the
cockpit; others have them only on the elevator and rudder; and some have them
only on the elevator. Some trim tabs are the ground-adjustable type only.
The tab is
moved in the direction opposite that of the primary control surface, to relieve
pressure on the control wheel or rudder control. For example, consider the
situation in which we wish to adjust the elevator trim for level flight.
("Level flight" is the attitude of the airplane that will maintain a
constant altitude.) Assume that back pressure is required on the control wheel
to maintain level flight and that we wish to adjust the elevator trim tab to
relieve this pressure. Since we are holding back pressure, the elevator will be
in the "up" position. The trim tab must then be adjusted downward so
that the airflow striking the tab will hold the elevators in the desired
position. Conversely, if forward pressure is being held, the elevators will be
in the down position, so the tab must be moved upward to relieve this pressure.
In this example, we are talking about the tab itself and not the cockpit
control.
Rudder and
aileron trim tabs operate on the same principle as the elevator trim tab to
relieve pressure on the rudder pedals and sideward pressure on the control
wheel, respectively.
Laminar
Flow Airfoil
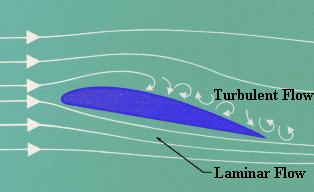
Laminar
Flow is
the smooth, uninterrupted flow of air over the contour of the wings, fuselage,
or other parts of an aircraft in flight. Laminar flow is most often found at
the front of a streamlined body and is an important factor in flight. If the
smooth flow of air is interrupted over a wing section, turbulence is created
which results in a loss of lift and a high degree of drag. An airfoil designed
for minimum drag and uninterrupted flow of the boundary layer is called a
laminar airfoil.
The Laminar
flow theory dealt with the development of a symmetrical airfoil section which
had the same curvature on both the upper and lower surface. The design was
relatively thin at the leading edge and progressively widened to a point of
greatest thickness as far aft as possible. The theory in using an airfoil of
this design was to maintain the adhesion of the boundary layers of airflow
which are present in flight as far aft of the leading edge as possible. on
normal airfoils the boundary layer would be interrupted at high speeds and the
resultant break would cause a turbulent flow over the remainder of the foil.
This turbulence would be realized as drag up the point of maximum speed at
which time the control surfaces and aircraft flying characteristics would be
affected. The formation of the boundary layer is a process of layers of air
formed one next to the other, ie; the term laminar is derived from the
lamination principle involved.
History of
Laminar Flow The P-51 Mustang is the first aircraft every intentionally designed to
use laminar flow airfoils. However, wartime NACA research data I have shows
that Mustangs were not manufactured with a sufficient degree of surface quality
to maintain much laminar flow on the wing. The RAE found that the P-63, despite
being designed with laminar airfoils, also was not manufactured with sufficient
surface quality to have much laminar flow.
The Mustang
was a mathematically designed airplane and the wing foil that was to be
classified as a "semi-empirical venture" by the British was cleared
for adoption on the new design. The wing section would be the only part of the
fighter which would be tested in a wind tunnel prior to the first test flight.
Due to the speculation of the success of the radical foil, the engineering
department was committed to adopt a more conventional airfoil within thirty
days of the tests in the event the wing did not come up to specifications. A
one quarter scale model of the wing was designed and constructed for tests in
the wing tunnel at the Caiifornia Institute of Technology.
The use of
this airfoil on the Mustang would greatly add to the drag reducing concept that
was paramount in all design phases of the airplane. The few applications of
this foil, prior to this time, had been handbuilt structures which were
finished to exacting tolerances. An absolutely smooth surface was necessary due
to the fact that any surface break or rough protrusion would interrupt the
airflow and detract from the laminar flow theory. Because of the exactness
required, the foil had been shelved by other manufacturers due to the
clearances and tolerances which are used in mass production. The engineers at
NAA approached this problem with a plan to fill and paint the wing surface to
provide the necessary smoothness. The foil which was used for the Mustang had a
thickness ratio of 15.1 percent at the wing root at 39 percent of the chord.
The tip ratio was 11.4 percent at the 50 percent chord line. These figures
provided the maximum thickness area at 40 percent from the leading edge of the
wing and resulted in a small negative pressure gradient over the leading 50-60
percent of the wing surface.
The B-24
bomber's "Davis" airfoil was also a laminar flow airfoil, which
predates the Mustang's. However, the designers of the B-24 only knew that their
airfoil had very low drag in the wind tunnel. They did not know that it was a
laminar flow airfoil.
There were
several aircraft modified by NACA, in the late 1930s, to have laminar flow test
sections on their wings. Hence, such aircraft as a modified B-18 were some of
the first aircraft to fly with laminar flow airfoils.
The boundary
layer concept is credited to the great German aerodynamicist, Ludwig Prandtl.
Prandtl hyposthesized and proved the existence of the boundary layer long
before the Mustang was a gleam in anyone's eye.
Example: First, lets get more
specific about what laminar flow is. The flow next to any surface forms a
"boundary layer", as the flow has zero velocity right at the surface
and some distance out from the surface it flows at the same velocity as the
local "outside" flow. If this boundary layer flows in parllel layers,
with no energy transfer between layers, it is laminar. If there is energy
transfer, it is turbulent.
All boundary
layers start off as laminar. Many influences can act to destabilize a laminar
boundary layer, causing it to transition to turbulent. Adverse pressure
gradients, surface roughness, heat and acoustic energy all examples of
destabilizing influences. Once the boundary layer transitions, the skin
friction goes up. This is the primary result of a turbulent boundary layer. The
old "lift loss" myth is just that - a myth.
A favorable
pressure gradient is required to maintain laminar flow. Laminar flow airfoils
are designed to have long favorable pressure gradients. All airfoils must have
adverse pressure gradients on their aft end. The usual definition of a laminar
flow airfoil is that the favorable pressure gradient ends somewhere between 30 and
75% of chord.
Now Consider
the finish on your car in non-rainy conditions. Dust and leaves have settled on
the hood's paint. We go for a drive. At once the leaves blow off. But the dust
remains. We speed up. Even if we go very fast, the dust remains because of the
thin layer of air that moves with the car. If you drive with dew on your car,
the dew will not so quickly be blown dry where the air flow has this thin
laminar layer. Downstream, where the laminar flow has become turbulent, the air
flow quickly dries the dew.
In the fifties
this was dramatically shown in a photograph of the top of a sailplane wing
(inflight) that had dew on it. A few tiny seeds had landed on forward area the
wing while on the ground. In flight these seeds, tiny though they were, reached
through the laminar layer and caused micro-turbulence causing the dew to be
blown dried in an expanding vee shaped area down stream of each tiny seed.
Additional
information
Profile drag
This comprises
two components: surface friction drag and normal pressure drag (form drag).
Surface
friction drag
This arises
from the tangential stresses due to the viscosity or "stickiness" of
the air. When air flows over any part of an aircraft there exists, immediately
adjacent to the surface, a thin layer of air called the boundary layer, within
which the air slows from its high velocity at the edge of the layer to a
standstill at the surface itself. Surface friction drag depends upon the rate
of change of velocity through the boundary layer, i.e. the velocity gradient.
There are two types of boundary layer, laminar and turbulent, the essential
features of which are shown in Fig 8. Although all combat aircraft surfaces
develop a laminar boundary layer to start with, this rapidly becomes turbulent
within a few per cent of the length of the surface. This leaves most of the
aircraft immersed in a turbulent boundary layer, the thickness of which
increases with length along the surface. The velocity and hence pressure
variations along the length of any surface can have adverse effects on the
behavior of the boundary layer, as will be discussed later.
Surface
friction drag can amount to more than 30% of the total drag under cruise
conditions.
Normal
pressure drag (form drag)
This also
depends upon the viscosity of the air and is related to flow separation. It is
best explained by considering a typical pressure distribution over a wing
section, as shown in Fig 4, first at low AOA and then at high AOA.
At low AOA the
high pressures near the leading edge produce a component of force in the
rearward (i.e. drag) direction, while the low pressures ahead of the maximum
thickness point tend to suck the wing section forward, giving a thrust effect.
The low pressures aft of the maximum thickness point tend to suck the wing
rearwards, since they act on rearward-facing surfaces. Without the influence of
the boundary layer, the normal pressure forces due to the above drag and thrust
components would exactly cancel.
There is a
favorable pressure gradient up to the minimum pressure point, with the pressure
falling in the direction of flow. This helps to stabilize the boundary layer.
Downstream of the minimum pressure point, however, the thickening boundary
layer has to flow against an adverse pressure gradient. Viscous effects reduce
momentum within the boundary layer, and the thickness of the layer further
increases so that the external flow "sees" a body which does not
appear to close to a point at the trailing edge. A narrow wake is formed as the
boundary layer streams off the section. This prevents the pressures on the
aft-facing surface of the wing section from recovering to the high value
obtaining near the stagnation point on the leading edge, as they would have
done if a boundary layer had not formed. There is thus a lower than expected
pressure acting on the aftfacing surface, giving rise to normal pressure drag.
In the low-AOA case this component is small, most of the profile drag being
made up of surface friction drag.
As the AOA of
the wing section is increased, the point of minimum pressure moves towards the
leading edge, with increasingly high suction being achieved. This means that
the pressure then has to rise by a greater extent downstream of the minimum
pressure point and that the length of wing surface exposed to the rising
pressure is increased. The resulting adverse pressure gradient becomes more
severe as AOA is increased. This has serious implications for the boundary
layer, which is always likely to separate from the wing surface under such
conditions.
The Swept Wing
The whole idea of sweeping
an aircraft's wing is to delay the drag rise caused by the formation of shock
waves. The swept-wing concept had been appreciated by German aerodynamicists
since the mid-1930s, and by 1942 a considerable amount of research had gone
into it. However, in the United States and Great Britain, the concept of the
swept wing remained virtually unknown until the end of the war. Due to the
early research in this area, this allowed Germany to successfully introduce the
swept wing in the jet fighter Messerschmitt ME-262 as early as 1941.
Early British and American
jet aircraft were therefore of conventional straight-wing design, with a
high-speed performance that was consequently limited. Such aircraft included
the UKGloster Meteor F.4 , the U.S. Lockheed F-80 Sooting Star
and the experimental U.S. jet, the Bell XP-59A Airacomet.
After the war German
advanced aeronautical research data became available to the United States Army
Air Force (USAAF) as well as Great Britain. This technology was then
incorporated into their aircraft designs. Some early jets that took advantage
of this technology were the North American F-86 Sabre, the Hawker
Hunter F.4 and the Supermarine Swift FR.5.
Not to be outdone, the
Soviet Union introduced the swept wing in the Mikoyan Mig-15 in 1947.
This aircraft was the great rival of the North American F-86 Sabre
during the Korean War.
Jet Engine Theory

Centuries
ago in 100 A.D., Hero, a Greek philosopher and mathematician, demonstrated jet
power in a machine called an "aeolipile." A heated, water filled
steel ball with nozzles spun as steam escaped.
Over
the course of the past half a century, jet-powered flight has vastly changed
the way we all live. However, the basic principle of jet propulsion is neither
new nor complicated.
Centuries
ago in 100 A.D., Hero, a Greek philosopher and mathematician, demonstrated jet
power in a machine called an "aeolipile." A heated, water filled
steel ball with nozzles spun as steam escaped. Why? The principle behind this
phenomenon was not fully understood until 1690 A.D. when Sir Isaac Newton in
England formulated the principle of Hero's jet propulsion "aeolipile"
in scientific terms. His Third Law of Motion stated: "Every action
produces a reaction... equal in force and opposite in direction."
The
jet engine of today operates according to this same basic principle. Jet
engines contain three common components: the compressor, the combustor,
and the turbine. To this basic engine, other components may be added,
including:
·
A nozzle
to recover and direct the gas energy and possibly divert the thrust for
vertical takeoff and landing as well as changing direction of aircraft flight.
·
An afterburneror
augmentor, a long "tailpipe" behind the turbine into which
additional fuel is sprayed and burned to provide additional thrust.
·
A thrust
reverser, which blocks the gas rushing toward the rear of the engine, thus
forcing the gases forward to provide additional braking of aircraft.
·
A fan
in front of the compressor to increase thrust and reduce fuel consumption.
·
An
additional turbine that can be utilized to drive a propeller or helicopter
rotor.
The Turbojet Engine
A turbojet
engine.
The
turbojet is the basic engine of the jet age. Air is drawn into the engine
through the front intake. The compressor squeezes the air to many times normal
atmospheric pressure and forces it into the combustor. Here, fuel is sprayed
into the compressed air, is ignited and burned continuously like a blowtorch.
The burning gases expand rapidly rearward and pass through the turbine. The
turbine extracts energy from the expanding gases to drive the compressor, which
intakes more air. After leaving the turbine, the hot gases exit at the rear of
the engine, giving the aircraft its forward push... action, reaction !
For
additional thrust or power, an afterburner or augmentor can be added.
Additional fuel is introduced into the hot exhaust and burned with a resultant
increase of up to 50 percent in engine thrust by way of even higher velocity
and more push.
The
Turboprop/Turboshaft Engine
A
turboprop, or turboshaft engine.
A
turboprop engine uses thrust to turn a propeller. As in a turbojet, hot gases
flowing through the engine rotate a turbine wheel that drives the compressor.
The gases then pass through another turbine, called a power turbine. This power
turbine is coupled to the shaft, which drives the propeller through gear
connections.
A
turboshaft is similar to a turboprop engine, differing primarily in the
function of the turbine shaft. Instead of driving a propeller, the turbine
shaft is connected to a transmission system that drives helicopter rotor
blades; electrical generators, compressors and pumps; and marine propulsion
drives for naval vessels, cargo ships, high speed passenger ships, hydrofoils
and other vessels.
The Turbofan Engine
A
high bypass turbofan engine.
A
turbofan engine is basically a turbojet to which a fan has been added. Large
fans can be placed at either the front or rear of the engine to create high
bypass ratios for subsonic flight. In the case of a front fan, the fan is
driven by a second turbine, located behind the primary turbine that drives the
main compressor. The fan causes more air to flow around (bypass) the engine. This produces greater thrust and
reduces specific fuel consumption.
A
low bypass turbofan engine.
For
supersonic flight, a low bypass fan is utilized, and an augmentor is added for
additional thrust.
|