Учебное пособие: Основы термодинамики
Учебное пособие: Основы термодинамики
ОСНОВЫ ТЕРМОДИНАМИКИ.
Глава 1. Основные понятия.
1.1.
Система.
Тело или группа тел, произвольно
выделяемая нами из внешнего мира, называется системой. Все, что не
входит в нашу систему, мы называем внешней средой или просто средой.
Изолированной или замкнутой системой называется такая система,
которая не может обмениваться со средой веществом и энергией. Система
называется адиабатической, если она не обменивается теплом с окружающей
средой (адиабарос – греческое – непереходимый).
Система называется закрытой,
если она не обменивается со средой веществом. Однако закрытая система может
изменять свой состав, если в ней протекает химическая реакция, которую
символически можно записать в виде: 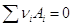 , где , где 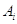 – некоторое химическое
соединение, – некоторое химическое
соединение, 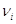 – стехиометрический
коэффициент, причем для исходных веществ – стехиометрический
коэффициент, причем для исходных веществ 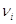 берется
со знаком «-», для продуктов реакции со знаком «плюс», например: берется
со знаком «-», для продуктов реакции со знаком «плюс», например: 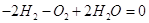 . .
Это уравнение показывает, что в
системе число молей водорода уменьшилось на 2, кислорода на 1, а число молей
воды увеличилось на 2.
1.2.
Параметры.
Все признаки, характеризующие систему и ее отношение к среде, называются параметрами
системы. Объем, показатель преломления, удельный вес, заряд, давление.
Термодинамическими параметрами называется объем, давление,
температура, энергия, концентрация веществ и производные только от этих
(теплоемкость, коэффициент расширения и т.д.). Все параметры делятся на два
класса – внутренние и внешние.
Параметры, определяемые положением не входящих в нашу систему внешних
тел, называются внешними параметрами. Объем системы, величина
поверхности определяются расположением внешних тел. Напряжение силового поля
зависит от положения источников поля – зарядов и токов, не входящих в систему.
Параметры называются внутренними, если они определяются совокупным
движением и распределением в пространстве тел и частиц, входящих в нашу
систему. Плотность, давление, энергия – внутренние параметры. Естественно, что
величины внутренних параметров зависят от внешних параметров.
Кроме того, параметры можно разделить и по другому признаку. Назовем интенсивными
параметрами такие, которые не зависят от количества вещества в системе,
например, давление, температура, коэффициент теплопроводности и т.п..
Параметры, которые зависят от количества вещества в системе, назовем экстенсивными,
к таковым относятся объем, энергия, энтропия и т.д.
Следует заметить, что отнесенные к единице количества вещества
экстенсивные параметры приобретают свойства интенсивных, например, мольный
объем, мольная энергия.
1.3.
Состояние.
Этот термин обозначает данную
совокупность значений параметров системы. Если изменяется хотя бы один, то
изменяется и состояние системы. Состояние называется стационарным, если
оно не меняется во времени.
Состояние называется равновесным, если в системе не только все
параметры постоянны, но и нет никаких стационарных потоков за счет действия
каких-либо внешних источников, т.е. неизменность не обусловлена никакими
внешними процессами.
1.4. Процесс.
Процессом называется ряд последовательных
изменений состояния системы. Процесс, после которого система возвращается в
первоначальное состояние, называется круговым процессом или циклом.
V = Const изохорический (греческое chora
– пространство),
p = Const изобарический (греческое baros
– тяжесть, вес),
t = Const изотермический (греческое therme
– жар, теплота),
Q = 0 адиабатический.
1.5.
Функции
состояния.
Свойство системы, не зависящее от
предыстории системы и полностью определяемое ее состоянием в данный момент
(т.е. совокупностью параметров), называется функцией состояния. Если Z – функция состояния и в состоянии 1
имеет величину 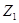 , а в состоянии 2
величину , а в состоянии 2
величину 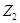 , то ее изменение при
переходе системы из состояния 1 в состояние 2 очевидно равно: , то ее изменение при
переходе системы из состояния 1 в состояние 2 очевидно равно: 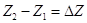 , где символ Δ
обозначает, что из значения функции , где символ Δ
обозначает, что из значения функции 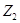 в
конечном состоянии мы вычли значение функции в
конечном состоянии мы вычли значение функции 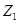 в
начальном состоянии. в
начальном состоянии.
Чтобы Z
имела свойства функции состояния необходимо и достаточно либо 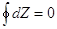 , если , если 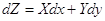 равенство перекрестных
производных. равенство перекрестных
производных.
Если процесс не круговой,
то 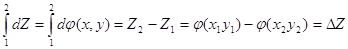 . .
Изменение функции
состояния не зависит от процесса перехода между 1 и 2:
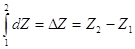 , ,  dZ = Xdx +
Ydy dZ = Xdx +
Ydy 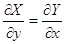 обратное справедливо. обратное справедливо.
Иными словами, бесконечно малое изменение функции состояния dZ обладает свойствами полного
дифференциала.
1.6.
Уравнение
состояния.
Изменение одного из свойств системы вызывает изменение, по крайней мере,
еще одного свойства, т.е. имеется функциональная зависимость термодинамических
параметров, которая носит название уравнения состояния.
Уравнение φ(p,v,T) =
0 является уравнением состояния чистого вещества, если 1) отсутствуют
электрические и магнитные поля,
2) эн. гравитации и
поверхности можно пренебречь,
3) v –
раномерно заполнен объем,
4) во всех частях
системы давление и температура постоянны.
pV = nRT – частный случай. Уравнение состояния различных
систем термодинамика берется в готовом виде.
Глава 2. Температура. I
закон термодинамики.
2.1. Температура.
Введем следующие два постулата:
1)
изолированная
система с течением времени всегда приходит в состояние равновесия и никогда
самопроизвольно из него выйти не может;
2)
если две системы
порознь находятся в равновесии с третьей, то они находятся и в равновесии между
собой.
Возьмем две равновесные изолированные системы и дадим им возможность
взаимодействовать друг с другом путем теплообмена. Очевидно, возможны два
варианта: либо равновесное состояние обеих систем не нарушится, либо нарушится,
но стечением времени эта двойная система (в целом изолированная) придет в новое
состояние равновесия (постулат 1). Отсюда можно сделать вывод, что
существует некоторый параметр, который может указать нарушается ли равновесное
состояние систем при тепловом контакте друг с другом или нет. Этот параметр
называется температурой.
Итак: любая термодинамическая система
обладает функцией состояния – температурой. Равенство температур во всех точках
есть условие теплового равновесия двух систем или двух частей одной и той же
системы.
Очевидно, во-первых, чтобы узнать
одинаковы ли температуры двух систем, совершенно необязательно их приводить в
тепловой контакт друг с другом, можно, согласно постулату 2, их привести
в тепловой контакт с некоей третьей системой, которую мы обычно называем
термометром.
Во-вторых, мы совершенно условно
принимаем, что температура той системы выше, которая при тепловом контакте
уменьшает свою энергию.
В-третьих, единицей измерения температуры является кельвин, который
обозначается буквой К. Международным соглашением приняты следующие
величины температур основных и вспомогательных реперных точек:
МПТШ – 68 (ред. 1975 г.)
Ратм Т,К t,
0C
Н2 тройная точка 6,939·10-2 13,81 -259,34
Ne кипение 1 27,102 -246,048
О2 тройная точка 1,54·10-3 54,361 -218,789
кипение 1 90,188 -182,962
Ar тройная точка 0,680 83,798 -189,352
Н2О тройная точка 6,03·10-3 273,16
0,01
Н2О кипение 1 373,15 100
Sn плавление 1 505,1181 231,9681
Zn плавление 1 692,73 419,58
Ag плавление 1 1235,08 961,43
Au плавление 1 1337,58 1064,43
вторичные реперные точки
(ред. 1975 г.)
Ne тройная 0,4283 24,561 -248,589
N2
тройная 0,1236 63,146 -210,004
N2
кипение 1 77,344 -195,806
Ar кипение 1 87,294 -185,856
CO2
сублим. 1 194,674 -78,476
Hg плавление 1 234,314 -38,836
H2O плавление 1 273,15 0
(С6Н5)2О
тр.точка 1 300,02 26,87
С6Н5СООН тр.точка 1 395,52 122,37
In плавление 429,74 156,634
Bi плавление 544,592 271,442
Pb плавление 600,652 327,502
Hg кипение 1 629,81 356,66
S кипение 1 717,824 444,674
Эвт. CuAl
плавление 821,41 548,26
Sb плавление 903,905 630,756
Al плавление 933,61 660,46
Cu плавление 1358,03 1084,88
Ni плавление 1728 1455
Co плавление 1768 1495
Pd плавление 1827 1554
Rh плавление 2236 1963
Al2O3 плавление 2327 2054
Ir плавление 2720 2447
Nb плавление 2750 2477
Mo плавление 2896 2623
W плавление 3695 3422
2.2. Внутренняя энергия системы. Работа и теплота.
В термодинамике под энергией понимают меру способности системы
совершать работу, при этом полную энергию системы разделяют на внешнюю и
внутреннюю. Внешняя энергия системы состоит из энергии движения системы
как целого и потенциальной энергии системы в поле внешних сил, а энергия всех
видов движения и взаимодействия частиц, входящих в систему, называется внутренней
энергией и обозначается U.

Очевидно, что внутренняя энергия состоит из энергии поступательного и
вращательного движения молекул, колебательного движения атомов,
межмолекулярного взаимодействия, внутриатомной энергии заполнения электронных
уровней, внутриядерной.
При росте температуры внутренняя энергия растет. При взаимодействии
системы с окружающей средой происходит обмен энергией. Способ передачи энергии,
связанный с изменением внешних параметров системы называется работой.
Способ передачи без изменения внешних параметров называется теплотой, а
процесс передачи теплообменом.
Количество энергии, переданное системой с изменением внешних параметров,
называется работой А. Работа – способ передачи упорядоченного
движения.
Работа и теплота Q не
являются видами энергии, а характеризуют лишь способ передачи энергии, т.е.
процесс. Состоянию системы не соответствует какое-либо значение А или Q. Мы будем считать, что A > 0, если система совершает
работу против сил сопротивления внешней среды, и Q > 0, если энергия передается системе. Теплоту и работу
измеряем в одних единицах.
2.3. I закон.
Любая термодинамическая система обладает функцией состояния – внутренней
энергией. Эта функция состояния возрастает на величину сообщенного системе
количества тепла dQ и уменьшается
на величину совершенной системой внешней работы dA. Для замкнутой системы справедлив закон постоянства энергии.
dU = dQ – dA (1).
Если в наличии конечное
изменение состояния, то имеем конечный процесс 1 → 2:
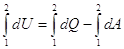 (2), (2),  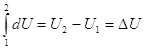 , ,  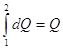 , ,
 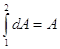 . .
(2) превращается в 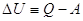 (3). U, Q и
А имеют одинаковую размерность. (3). U, Q и
А имеют одинаковую размерность.
2.4. Работа расширения.
Пусть наша система характеризуется только одним внешним параметром
объемом V. Давление Р характеризует
взаимодействие системы с внешней средой и измеряется силой, отнесенной к
единице поверхности. Если система находится в равновесии, то давление одинаково
во всех частях системы и равняется внешнему давлению. Тогда работа изменения
объема системы:
  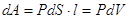 , , 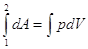 , , 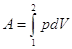 - зависит от р=р(V). - зависит от р=р(V).
V = Const, то dV = 0, dA=0, то A=0, т.е. ΔU = 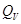 , в этом случае тепловой эффект , в этом случае тепловой эффект 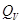 равен изменению функции состояния. равен изменению функции состояния.
p = Const, то 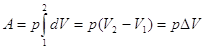 ; T = Const, то ; T = Const, то 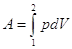 . В этом случае
необходимо знать уравнение состояния системы . В этом случае
необходимо знать уравнение состояния системы 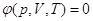 . .
Если система - идеальный
газ, то 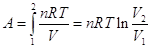 , поскольку pV = nRT, А , поскольку pV = nRT, А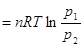 в связи с тем, что при T=const p1V1 = p2V2. в связи с тем, что при T=const p1V1 = p2V2.
R = 0,082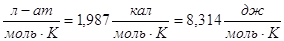 Это стоит запомнить. Это стоит запомнить.
Кроме того, при Т = Const для идеального газа U = Const, dU = 0, A = Q, т.е. все тепло, полученное идеальным газом, перешло в
работу.
Для адиабатического процесса dQ = 0 (Q = 0), dU = -dA, -ΔU = A т.е. положительная работа совершается за счет
уменьшения U.
2.5. Теплота и
теплоемкость.
Теплоемкостью системы называется отношение количества тепла, сообщенного
системе в каком-либо процессе, к соответствующему изменению температуры:
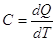 1 кал = 4,1840 дж, 1 дж = 107
эрг (СИ) 1 кал = 4,1840 дж, 1 дж = 107
эрг (СИ)
Поскольку Q-функция
процесса, то 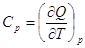 , а , а 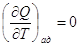 , , 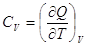 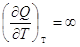 . .
Связь между Ср и Сv для любых систем найдем следующим
образом.
dQ = dU + pdV I закон.
Выберем в качестве независимых переменных объем и температуру, тогда
внутренняя энергия:
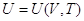 и и 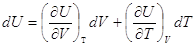 , ,
а  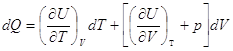 . .
Разделим правую и левую
части на dT, получим:
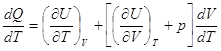 . .
Отношение 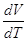 есть отношение
приращений независимых переменных, то есть величина неопределенная, и чтобы
снять неопределенность, необходимо указать характер процесса. Пусть процесс
изохорный. есть отношение
приращений независимых переменных, то есть величина неопределенная, и чтобы
снять неопределенность, необходимо указать характер процесса. Пусть процесс
изохорный.
V = Const 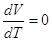 и и 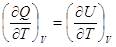 =СV. =СV.
Отсюда 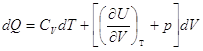 . .
Далее при p
= Const 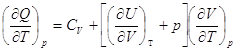 = Ср = Ср
И для любых систем 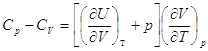  . .
Для идеальных газов 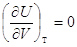 (Строго докажем при II
законе). (Строго докажем при II
законе).
А поскольку pV = RT, то 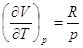 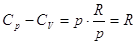 . .
Заметим, что 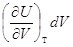 – работа, которую совершает система, преодолевая
внутренние силы сцепления. Производная – работа, которую совершает система, преодолевая
внутренние силы сцепления. Производная 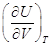 имеет
размерность давления и называется внутренним давлением. имеет
размерность давления и называется внутренним давлением.
2.6. Уравнение адиабаты
идеального газа.
dQ = dU + pdV.
Для идеального газа dU = CVdT,
следовательно, dQ = CvdT + pdV, и если процесс адиабатический dQ = 0, то
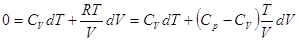 , ,
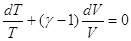 , где , где 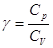 . .
CV и Cp для идеального газа не зависят от температуры:
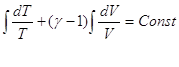
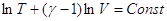 , ,
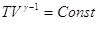
Поскольку 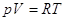 , то , то 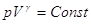 Уравнение Пуассона Уравнение Пуассона
Для газов величину γ можно определить, измеряя скорость звука в
газе:
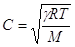 – скорость звука в газе, имеющего мольную массу М. – скорость звука в газе, имеющего мольную массу М.
Глава 3. Термохимия.
3.1 Энтальпия.
Если система характеризуется только одним внешним параметром V, т.е. может совершаться только
работа расширения, тогда первый закон может быть записан в виде: 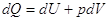 . .
Если 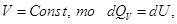 т.е. тепловой процесс
эффекта равен изменению функции состояния. Найдем такую функцию состояния,
изменение которой равно тепловому эффекту при постоянном давлении. Для этого
выражение для I закона необходимо преобразовать так,
чтобы давление находилось под знаком дифференциала. Обратим внимание, что т.е. тепловой процесс
эффекта равен изменению функции состояния. Найдем такую функцию состояния,
изменение которой равно тепловому эффекту при постоянном давлении. Для этого
выражение для I закона необходимо преобразовать так,
чтобы давление находилось под знаком дифференциала. Обратим внимание, что
d(pV) = pdV + Vdp и pdV = = d(pV)
– Vdp, а подстановка в выражение для I закона дает:
dQ = dU + d(pV)
– Vdp = d(U + pV)
– Vdp = dH -Vdp
H ≡ U
+ pV
|
–
функция состояния называется энтальпией.
|
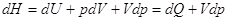 . При . При 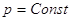 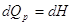 . .
Выберем в качестве независимых переменных Т и р, тогда:
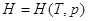
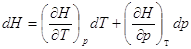
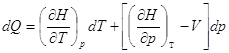
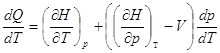
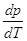 – отношение приращения независимых переменных
является неопределенной величиной, чтобы избежать этого нужно указать
конкретный процесс. Если p = Const, то – отношение приращения независимых переменных
является неопределенной величиной, чтобы избежать этого нужно указать
конкретный процесс. Если p = Const, то 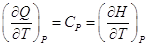
Очевидно, есть определенная
симметрия между U и H:
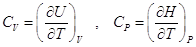
3.2. Теплоты химических
реакций. Закон Гесса.
При химических реакциях происходит изменение U, поскольку U продуктов реакции отличается от U исходных веществ. Пусть U2 – внутренняя энергия продуктов
реакции, U1 – внутренняя энергия исходных
веществ, ΔU = U2 –U1 - изменение U в результате химического процесса.
Аналогично для энтальпии. Изучением теплот химических реакций занимается
термохимия.
Q - теплота химической реакции, зависит от способа проведения химической
реакции. 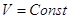 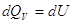 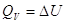 , ,
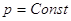 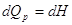 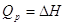 . .
Т.о., в этих случаях Q
равна изменению функции состояния и поэтому не зависит от пути процесса, а лишь
от начального и конечного состояния.
Закон Гесса (1836).
Если из данных исходных веществ можно получить заданные конечные продукты
разными путями, то суммарная теплота процесса (при 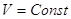 или при или при 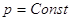 ) на одном каком-нибудь пути равна
суммарной теплоте процесса на любом другом пути, т.е. не зависит от пути
перехода от исходных вществ к продуктам реакции. ) на одном каком-нибудь пути равна
суммарной теплоте процесса на любом другом пути, т.е. не зависит от пути
перехода от исходных вществ к продуктам реакции.
3.3. Термохимические
уравнения.
Для облегчения расчетов следует поступать
так если p=Const,
то
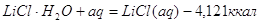
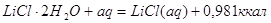
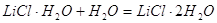
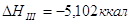
Уравнения химических
реакций вместе с тепловыми эффектами называются термохимическими уравнениями и
с ними можно оперировать как с алгебраическими уравнениями. Запомним, что если:
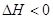 Qp выделяется, Qp выделяется,
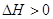 Qp
поглощается Qp
поглощается
3.4. Связь между Qp и QV
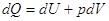 . .
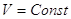 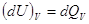 , ,
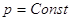 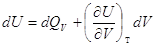 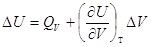 , ,
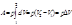 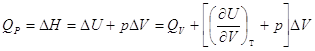
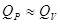 , если реагенты только жидкие или твердые вещества , если реагенты только жидкие или твердые вещества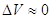 . .
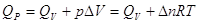 , где Δn – изменение числа молей газообразных участников реакции: , где Δn – изменение числа молей газообразных участников реакции:
CO + H2O
= CO2 + H2 Δn = 0 Qp
= Qv
N2
+ 3H2 = 2NH3 Δn = -2 Qp
< Qv
Zn (тв) + H2SO4 (ж)
= ZnSO4 (p-p) + H2 (газ)
Δn = +1 Qp > Qv
Но для реакции в конденсированной системе:
CuSO4
+ 5H2O (ж)
= CuSO4 5H2O (кр)
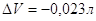 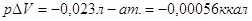 ,т.е. разница между QP и QV очень мала, ею можно пренебречь. ,т.е. разница между QP и QV очень мала, ею можно пренебречь.
3.5. Теплота образования
химических соединений.
Теплотой образования
химического соединения называется тепловой эффект реакции образования одного моля данного
соединения из соответствующих чисел молей простых веществ.
Стандартной теплотой образования 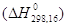 называется
теплота образования химического соединения из простых веществ, находящихся в
стандартных условиях, причем продукты реакции также находятся в стандартных
условиях. За стандартные условия приняты: температура 25 0С
(298,15 К) и 1 атм (760 торр). называется
теплота образования химического соединения из простых веществ, находящихся в
стандартных условиях, причем продукты реакции также находятся в стандартных
условиях. За стандартные условия приняты: температура 25 0С
(298,15 К) и 1 атм (760 торр).
Замечания:
1.
Стандартная теплота образования
простого вещества равно нулю
2.
Простое вещество имеет то
агрегатное состояние, в котором оно находится в стандартных условиях.
С (графит) 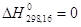
С (алмаз) 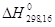 = 453,2 кал/г-ат = 453,2 кал/г-ат
О2 (кислород) 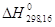 = 0 кал/моль = 0 кал/моль
О3 (озон) 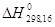 = 34,0 ккал/моль = 34,0 ккал/моль
Исключение: для фосфора –
белый фосфор
Теплоты образования химических соединений обычно вычисляются по
экспериментальным теплотам соответствующих химических реакций, например, для I2O5 :
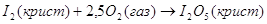 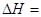 ? ?
1. 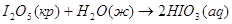 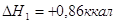
2. 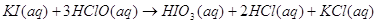 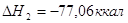
3. 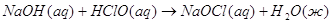 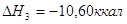
4. 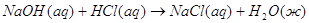 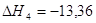 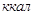
5. 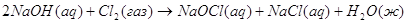 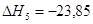 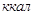
6. 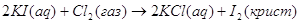 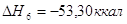
7. 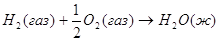 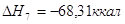
8. 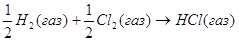 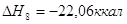
9. 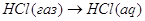 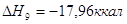
По закону Гесса: 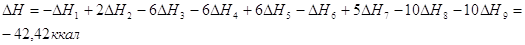
Теплоты образования химических соединений приводятся в справочниках
физико-химических величин и для вычисления теплового эффекта химических реакций
необходимо из суммы теплот образования продуктов реакции вычесть сумму теплот
образования исходных веществ: 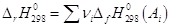
Заметим, что в дальнейшем
изложении мы введем еще ряд функций состояния и для них закон Гесса также
справедлив.
3.6. Зависимость теплового
эффекта химической реакции от температуры.
Если Hi мольная энтальпия химического соединения, то 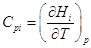 . Очевидно, что для
некоторой химической реакции . Очевидно, что для
некоторой химической реакции 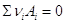 и и 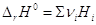 . .
Дифференцирование по температуре, разделение переменных и интегрирование
в интервале от Т1 до Т2 дают (р = const):
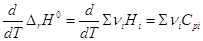 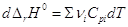
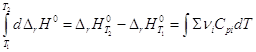
и 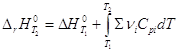 уравнение
Кирхгоффа уравнение
Кирхгоффа
Аналогично для ΔU
и Cv.
Глава 4. Второй закон.
4.1. Определение.
Каждая термодинамическая система обладает функцией состояния -энтропией.
Энтропия процесса вычисляется следующим образом. Система переводится из
начального состояния в соответствующее конечное состояние через последовательность
состояний равновесия, вычисляются все подводимые при этом к системе порции
тепла dQ, делятся каждая на соответствующую
ей абсолютную температуру Т источника теплоты и все полученные таким
образом значения суммируются: 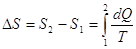 и и 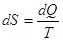 . .
При реальных (неидеальных) процессах энтропия замкнутой (изолированной)
системы возрастает 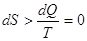 , т.е. , т.е. 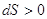 . .
Энтропия – способность к превращению (Клаузиус)
По I закону 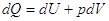 и
для идеального газа и
для идеального газа
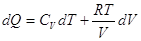 и и 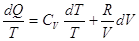 . .
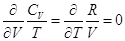 , т.е. для идеального газа , т.е. для идеального газа 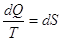 обладает
свойствами полного дифференциала, т.е. S есть функция
состояния. обладает
свойствами полного дифференциала, т.е. S есть функция
состояния.
|
Распространение 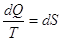 на все системы и есть II закон на все системы и есть II закон
|
4.2. Другие формулировки
Тепло не может само по
себе перейти от системы с меньшей температурой к системе с большей температурой
(Клаузиус).
Невозможно получать работу, только охлаждая отдельное тело ниже
температуры самой холодной части окружающей среды (Кельвин).
4.3. Обратимые и
необратимые процессы.
Процесс называется равновесным, если в прямом и обратном направлении
проходит через одни и те же состояния бесконечно близкие к равновесию. Работа
равновесного процесса имеет максимальную величину по сравнению с неравновесными
процессами и называется максимальной работой.
Если равновесный процесс протекает в прямом, а затем в обратном
направлении так, что не только система, но и окружающая среда возвращается в
исходное состояние и в результате процесса не остается никаких изменений во
всех участвовавших в процессе телах, то процесс называется обратимым.
Обратимый процесс – такая же абстракция, что и идеальный газ.
Крайние случаи необратимых процессов:
переход энергии от горячего тела к холодному в форме теплоты при конечной
разнице температур, переход механической работы в теплоту при трении,
расширение газа в пустоту, диффузия, взрывные процессы, растворение в
ненасыщенном растворе.
Эти необратимые процессы идут самопроизвольно без воздействия
извне и приближают систему к равновесию.
4.4. Изменение энтропии в различных процессах.
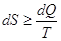 , причем знак = относится к обратимым процессам, а
знак > к необратимым. , причем знак = относится к обратимым процессам, а
знак > к необратимым.
Если требуется вычислить энтропию необратимого процесса необходимо
провести обратимый процесс между теми же самыми конечным и начальным состоянием
(используем тот факт, что энтропия – функция состояния).
а) Изотермический процесс:
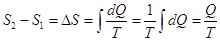 , Q – часто это скрытая теплота фазовых переходов. , Q – часто это скрытая теплота фазовых переходов.
б) Изменение температуры при  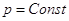 : :
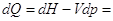 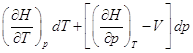 , следовательно , следовательно 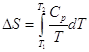 , т.к. , т.к. 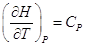
Энтропия необратимого
процесса: 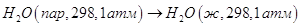
Теплота конденсации при 298
К равна – 10519 кал, 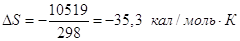
Ответ, очевидно, неверен, поскольку процесс необратимый. Проведем его
обратимо:  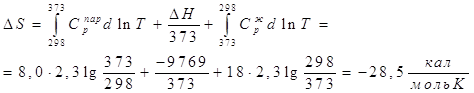
(-9769 – теплота конденсации при 373 К)
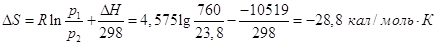
Заметим, что действительно 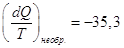 меньше, чем меньше, чем 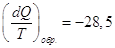 . .
4.5. Закон Джоуля
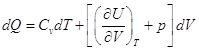 , ,
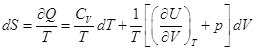 – это полный дифференциал, следовательно – это полный дифференциал, следовательно 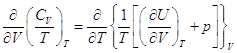 . .
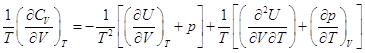 , , 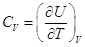
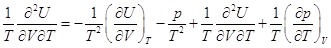
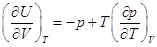 . .
Для идеального газа 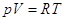 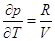 и и 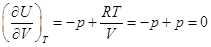 , ,
Для любых систем 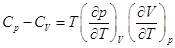 , ,
Для газа Ван-дер-Ваальса 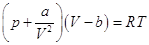 и и 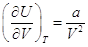 . .
4.6. Постулат Планка.
Абсолютная энтропия.
Зададимся вопросом, каково изменение энтропии некоего процесса, который
протекает при температуре около абсолютного нуля. Например, имеем две
кристаллические модификации металлического олова: низкотемпературную, α - Sn,
и высокотемпературную – обычное белое олово, β – Sn. Они находятся
в равновесии при 14 0С (287 К), теплота равновесного
превращения 497 кал/моль, а энтропия его 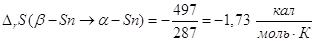
Легко сообразить, чтобы дать ответ на поставленный вопрос, необходимо
взять β – Sn при 0 К, нагреть до температуры 14 0С,
равновесно превратить β – Sn в α – Sn, и затем охладить
α – Sn до абсолютного нуля, тогда суммарное изменение энтропии
будет:
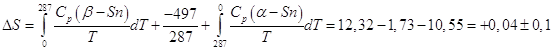 , ,
т.е. изменение энтропии в
пределах ошибок опыта равно нулю, а отсюда следует, что энтропии α – Sn
и β – Sn одинаковы.
Исходя из многочисленных подобных экспериментов (мы их обсудим позднее в
гл.16), Планк выдвинул постулат: энтропия идеального кристаллического
тела при абсолютном нуле равна нулю.
Абсолютные
энтропии веществ, измеренные экспериментально или вычисленные теоретически,
приводятся в справочниках термодинамических величин (где и теплоты
образования).
Глава 6. Равновесие в однокомпонентных гетерогенных системах.
Уравнение Клапейрона – Клаузиуса
6.1. Определения.
Фазой называется совокупность частей
системы, обладающих одинаковыми термодинамическими свойствами. Система,
состоящая из одной фазы, называется гомогенной, из двух или более – гетерогенной.
Фаза более общее понятие, чем индивидуальное вещество. Система может состоять
из одного вещества, но быть гетерогенной (вещество находится в системе в виде
разных агрегатных состояний или кристаллических модификаций). Система может
быть гомогенной, но содержать несколько химических соединений, пример этого –
растворы.
Назовем составляющими веществами системы такие химические
соединения, которые могут быть выделены из системы, и существовать отдельно от
нее. Назовем независимыми компонентами такие составляющие вещества,
концентрации которых могут изменяться независимо. Если в системе не протекают
химические реакции, то все вещества, составляющие систему, являются независимыми
компонентами.
Но в случае фактического протекания химических реакций концентрации
только части веществ могут изменяться независимо, поэтому число независимых компонентов
равно числу составляющих веществ минус число химических реакций, которые
фактически протекают в системе.
6.2. Условия равновесия и
направление самопроизвольного процесса в однокомпонентной гетерогенной системе.
Пусть гетерогенная однокомпонентная система
имеет две фазы (΄) и (˝), а мольные энергии Гиббса компонента в
каждой из фаз G΄ и G˝ соответственно. Пусть давление и температура постоянны, а
изменение чисел молей компонента в фазе (´) равно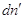 , в фазе (´) , в фазе (´) 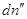 , тогда изменение энергии
Гиббса системы равно: , тогда изменение энергии
Гиббса системы равно: 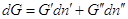 . .
Если система закрытая, то 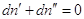 , и , и 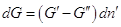 . .
При равновесии 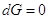 , а это возможно, когда , а это возможно, когда 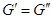 , т.е. при равновесии
мольные энергии Гиббса компонента в фазах равны. , т.е. при равновесии
мольные энергии Гиббса компонента в фазах равны.
Самопроизвольный процесс в системе
может протекать только в сторону уменьшения энергии Гиббса системы, т.е. 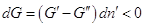 . Положим, для
определенности, что . Положим, для
определенности, что 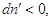 тогда тогда 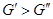 , если же. Это значит, что
компонент самопроизвольно переходит из той фазы, где его мольная энергия Гиббса
больше, в ту фазу, где его мольная энергия Гиббса меньше. , если же. Это значит, что
компонент самопроизвольно переходит из той фазы, где его мольная энергия Гиббса
больше, в ту фазу, где его мольная энергия Гиббса меньше.
Изменим давление и температуру на
бесконечно малые величины dT и
dp, тогда очевидно, что если система остается равновесной
и гетерогенной 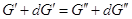 следовательно, и следовательно, и 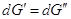 . .
6.3. Уравнение
Клапейрона-Клаузиуса.
Очевидно, что 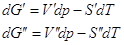 , где V’,V’’,S’,S” мольные объемы и мольные энтропии компонента в фазах
(‘) и (“). Из условий равновесия , где V’,V’’,S’,S” мольные объемы и мольные энтропии компонента в фазах
(‘) и (“). Из условий равновесия 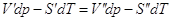 или или 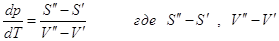 - изменение энтропии и объема при переходе 1 моля
компонента из фазы (‘) в фазу (“), т.е. это мольные изменения энтропии и объема
фазового превращения. - изменение энтропии и объема при переходе 1 моля
компонента из фазы (‘) в фазу (“), т.е. это мольные изменения энтропии и объема
фазового превращения.
Учитывая, что фазовое превращение
рассматривалось как равновесное и изотермическое, то 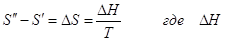 - теплота фазового
превращения и окончательно: - теплота фазового
превращения и окончательно: 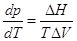 уравнение
Клапейрона–Клаузиуса. уравнение
Клапейрона–Клаузиуса.
Заметим, что в уравнении Клапейрона
ΔH и ΔV относятся к одноименным процессам и на одно и тоже
количество вещества.
6.4. Фазовое равновесие в
конденсированных системах.
Конденсированной системой называется такая, в которой не
имеется в наличии газообразная фаза, а только твердые или жидкие или те и
другие вместе.
Наиболее интересным является
равновесие кристалл ↔ жидкость. Поскольку теплота плавления всегда
положительна, знак производной 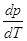 будет зависеть от знака ∆V. Для большинства веществ ∆V>0 (Vж > Vкр), и производная положительна, т.е.
температура лавления будет расти с ростом давления. Однако у некоторых веществ
(H2O, Ga, Bi, Sb, Ge, Si и др.) при плавлении происходит уменьшение объема, Vж < Vкр, и температура плавления понижается
с повышением давления. Так для воды будет зависеть от знака ∆V. Для большинства веществ ∆V>0 (Vж > Vкр), и производная положительна, т.е.
температура лавления будет расти с ростом давления. Однако у некоторых веществ
(H2O, Ga, Bi, Sb, Ge, Si и др.) при плавлении происходит уменьшение объема, Vж < Vкр, и температура плавления понижается
с повышением давления. Так для воды 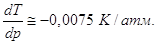
Если предположить, что для
конденсированных систем ∆H и
∆V
не зависят ни от
давления, ни от температуры, то уравнение Клапейрона-Клаузиуса легко
интегрируется 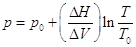 . .
Интересным является рассмотрение
равновесия С (графит) →С (алмаз). Использование справочных данных
для энтальпий образования и энтропий графита и алмаза дает для этого
превращения 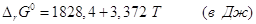 , откуда видно, что при
любых температурах , откуда видно, что при
любых температурах 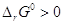 . Но поскольку . Но поскольку 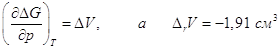 , то с увеличением давления
∆rG
должна уменьшаться и при данной температуре графит и алмаз находятся в
равновесии, тогда когда ∆rG = 0. Предположив, что ∆V не зависит от давления, получим
после интегрирования. , то с увеличением давления
∆rG
должна уменьшаться и при данной температуре графит и алмаз находятся в
равновесии, тогда когда ∆rG = 0. Предположив, что ∆V не зависит от давления, получим
после интегрирования.
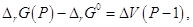 откуда откуда 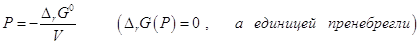 . .
Подставив численные значения ∆rG0 и ∆V получим Р (атм) = 9448 + 17,42 Т
При 300 К Р=14670
атм.
1000 К Р=26870
атм.
1500 К Р=35580
атм., т.е. равновесные давления имеют порядок десятков тысяч атм.
Далее 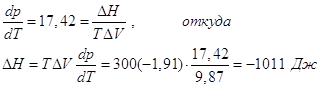 , и мы видим, что при высоком
давлении поменялся даже знак теплового эффекта. Действительно, возьмем
уравнение Гиббса-Гельмгольца: , и мы видим, что при высоком
давлении поменялся даже знак теплового эффекта. Действительно, возьмем
уравнение Гиббса-Гельмгольца:
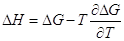 и возьмем производную по давлению: и возьмем производную по давлению:
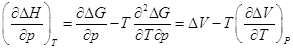 . .
После интегрирования и ряда упрощений
имеем:
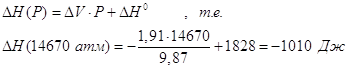 . .
6.5. Интегрирование
уравнения Клапейрона-Клаузиуса для процесса парообразования.
Переход жидкости в пар называют испарением,
обратный процесс конденсацией. Испарение твердых тел называют возгонкой
или сублимацией, обратный – кристаллизацией. Пар, который
находится в равновесии с конденсированной фазой, называется насыщенным паром.
Поскольку теплота парообразования
положительна, а мольный объем пара больше мольного объема конденсированной
фазы, это значит, что производная в уравнении Клапейрона-Клаузиуса 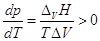 т.е. с ростом температуры
давление насыщенного пара увеличивается. т.е. с ростом температуры
давление насыщенного пара увеличивается.
При температурах, далеких от
критических, мольный объем пара много больше мольного объема конденсированной
фазы, поэтому последним можно пренебречь, а если в этой области температур
насыщенный пар подчиняется уравнению состояния идеального газа, то: 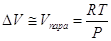 , и уравнение Клапейрона-Клаузиуса
можно представить в виде: , и уравнение Клапейрона-Клаузиуса
можно представить в виде: 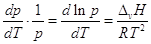 . .
В нешироком интервале температур
теплоту испарения можно считать постоянной и взятие определенного интеграла
дает: 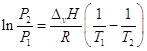 . .
Таким образом, если известна ∆v H, то, зная давление насыщенного пара
вещества при одной температуре, можно рассчитать давление насыщенного пара при
другой температуре. С другой стороны, определив давление насыщенного пара при
двух (по крайней мере) температурах, можно рассчитать теплоту испарения.
Взятие неопределенного интеграла дает
(при ∆v H =
const) 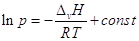 или или 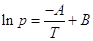 , где А и В – константы, характерные
для данного вещества. Это уравнение, линейное в координатах ln p – 1/T,
дает прямую линию в значительном интервале температур. Более точным является уравнение
Антуана: , где А и В – константы, характерные
для данного вещества. Это уравнение, линейное в координатах ln p – 1/T,
дает прямую линию в значительном интервале температур. Более точным является уравнение
Антуана: 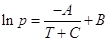 , где А, В, С –
константы. , где А, В, С –
константы.
Практически полезным может оказаться правило
Трутона: энтропия испарения вещества в нормальной точке кипения (при 1
атм.) равна приблизительно 90 Дж/моль*К. Тогда в уравнение Клапейрона-Клаузиуса
входит только одна константа Тнтк – температура нормальной точки
кипения:
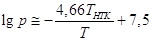 . .
По этому уравнению удобно
рассчитывать температуру перегонки органических соединений под пониженным
давлением. Однако следует отметить, что правило Трутона соблюдается только для
«нормальных» жидкостей, т.е. таких молекулы которых не ассоциированы в жидкой
фазе (как у воды за счет водородных связей), а также, если пары не состоят из
полимерных или диссоциированных молекул.
Для уксусной кислоты прямые
определения теплоты испарения в калориметре при температуре кипения СН3СООН
равной 391К дает величину 406 Дж/г. С другой стороны при 363 К давление пара
293 торр, при 391К и 760 торр. Заменив производную в уравнении
Клапейрона-Клаузиуса отношением конечных приращений имеем:
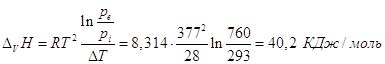 . .
Мольная масса СН3СООН
равна 60, тогда из калориметрических данных:
 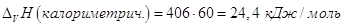 . .
Расхождение между этими двумя
значениями связано с тем, что для получения одного моля пара необходимо
испарить больше, чем 60 г СН3СООН, следовательно, мольная масса пара
СН3СООН равна:
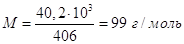 , отсюда легко сообразить, что пары
уксусной кислоты в этом температурном интервале димеризованы примерно на 2/3. , отсюда легко сообразить, что пары
уксусной кислоты в этом температурном интервале димеризованы примерно на 2/3.
Насыщенный пар обладает еще рядом
интересных свойств. Рассмотрим некоторые из них.
Пусть в гетерогенной системе при
температуре Т находится 1 моль вещества, причем в равновесии находятся m молей пара и 1-m молей жидкой фазы. Пусть
теплоемкость пара Сп, жидкости Сж, изменяем температуру
от Т до T+dT, при этом испаряется масса жидкости dm, тогда затраты тепла dQ можно представить в виде соотношения:
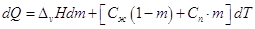 . .
Разделим правую и левую части на Т,
имеем:
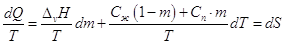 . .
Следовательно, справедливо: 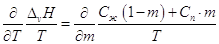 , ,
после дифференцирования имеем 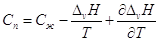 . .
По уравнению Кирхгоффа 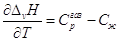 и и 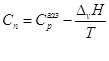 , ,
т.е. теплоемкость насыщенного пара не
равна изобарной теплоемкости того же газообразного вещества.
Следует также иметь в виду, что
введение постороннего (инертного) газа изменяет давление насыщенного пара при
неизменной температуре, даже если газ не растворяется в жидкости. Это
происходит вследствие влияния общего давления на свойства конденсированной фазы
(возрастает ее мольная энергия Гиббса). Действительно, при T=const:
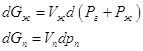 , где Рг – давление постороннего
газа, Рж давление насыщенного пара, Vж и Vп - мольные
объемы жидкости и пара. Поскольку по условию равновесия dGж =dGп, то: , где Рг – давление постороннего
газа, Рж давление насыщенного пара, Vж и Vп - мольные
объемы жидкости и пара. Поскольку по условию равновесия dGж =dGп, то:
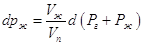 . .
Взятие интеграла от Рг = 0 до Рг
приводит к уравнению: 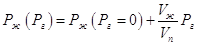
Поскольку дробь Vж/Vn невелика (для воды при 373 К она
равна 5,9∙10-4), то влияние постороннего газа сказывается
только при высоких давлениях.
Например, для воды под давлением
водорода при 373 К
|
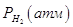
|
|
25 |
200 |
600 |
1000 |
|
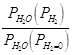
|
Эксп. |
1,018 |
1,19 |
1,66 |
2,35 |
| Расч. |
1,015 |
1,12 |
1,35 |
1,802 |
Глава 7. Термодинамические свойства многокомпонентных систем.
Растворы. Химический потенциал.
7.1. Определения.
Раствором называется гомогенная, молекулярно-дисперсная
система, состав которой можно изменять непрерывно в некотором конечном или
бесконечном интервале.
По агрегатному состоянию растворы разделяются на твердые, жидкие и
газообразные. Если растворитель и растворенное вещество имеют разные агрегатные
состояния, то растворителем рассматривают обычно то вещество, агрегатное
состояние которого совпадает с агрегатным состоянием раствора. Если же
компоненты раствора и раствор имеют одинаковое агрегатное состояние, то за растворитель
считают то вещество, которого больше, хотя для термодинамики это безразлично.
Состав раствора измеряется его концентрацией. Существуют следующие
основные определения концентрации:
мольная доля (х) –
число молей вещества в 1 моле раствора;
моляльность (m)
– число молей растворенного вещества в 1000 г растворителя;
молярность (с) –
число молей растворенного вещества в 1 л раствора;
массовое содержание (р)
– число грамм растворенного вещества в 100 г раствора.
В основном мы будем
пользоваться мольной долей. Очевидно, что
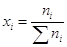 , а , а 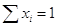 . .
Если М0 и М мольные массы растворителя и растворенного
вещества, а d – плотность раствора,
г/см3, то переход от одной концентрации к другой можно представить
следующими формулами (раствор, естественно, бинарный):
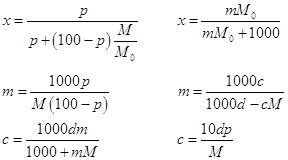
7.2. Характеристические функции многокомпонентных
систем.
Первый и второй законы термодинамики, из которых следуют фундаментальные
уравнения, были получены для закрытых систем, т.е. систем, процессы в которых
не приводят к изменению количества компонентов. Реально же чаще встречаются
системы, в которых при различных процессах изменяются количества компонентов.
Это может происходить, скажем, при фазовых превращениях или вследствие
протекания химической реакции. При этом может изменяться состав, как отдельных
частей, так и системы в целом.
Поэтому
внутренняя энергия (и другие функции состояния) открытых систем будут
изменяться не только за счет сообщения системе теплоты и произведенной системой
работы, но и за счет изменения состава системы. Следовательно для открытых
систем характеристические функции будут функциями не только их двух
естественных переменных, но и функциями числа молей всех веществ , составляющих
систему:
U = U ( S, v, n1……………….nk
),
H = H ( S,
p, n1 ………….. nk ),
F = F ( T,
v, n1…………… nk ),
G = G ( T,
p, n1……………nk ).
Полный дифференциал внутренней энергии открытой системы
можем записать как: 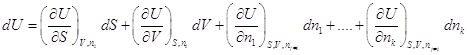 . .
Индекс nj≠i означает,
что число молей других веществ, кроме данного, не изменяется.
Но если открытая система изменяет свое состояние при постоянном составе
(все ni =const), то она ничем не отличается от
закрытой системы, поэтому:
 и и 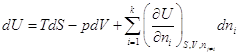 . .
Гиббс назвал частную
производную 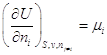 химическим потенциалом i – компонента. химическим потенциалом i – компонента.
Аналогично: 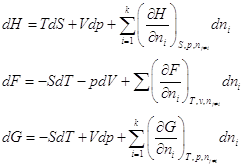 . .
Поскольку H≡ U + pV, F ≡ U – TS, G ≡ U – TS + pv, то dH = dU + pdV + Vdp, dF = dU – TdS – SdT, dG = dU – TdS – SdT + Vdp + pdV.
и подставив сюда 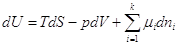
получаем: 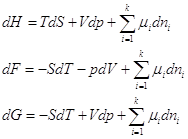
Сравнив выражение для
полных дифференциалов характеристических функций, получаем: 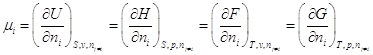 , ,
т.е. химический потенциал компонента
равен приращению характеристической функции системы при добавлении одного моля
данного компонента при условии, что естественные переменные и состав системы
остаются постоянными, т.е. система достаточно велика.
7.3. Однородные функции. Уравнение Гиббса-Дюгема.
Функция многих переменных, например F(x,y,z), называется однородной функцией порядка k, если она обладает следующим
свойством:
F (tx, ty, tz) = tk F (x, y, z),
(например, F = x3 +x2y + y2x + z3 является однородной функцией 3-его порядка).
Однородные функции обладают следующим свойством (теорема Эйлера): 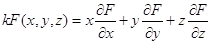 . .
Доказательство теоремы Эйлера следующее:
Если f
= f (x1, x2,…xn ), а каждое xi = φ(t), то 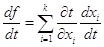 . .
Пусть F (x, y, z ) - однородная функция порядка k, положим x = tα, y=tβ, z = tγ, тогда 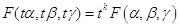 . .
Продифференцируем по t:
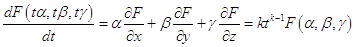 . .
Положим t
= 1,тогда α = x,
β = y, γ = z и
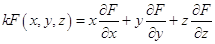 , что и требовалось
доказать. , что и требовалось
доказать.
Если температура и давление постоянны, то энергия Гиббса является
функцией только числа молей компонентов: G = G (n1, n2, …nk ) и легко сообразить, что она является однородной
функцией первого порядка относительно числа молей компонентов и по теореме
Эйлера (k = 1):
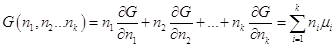 . .
После дифференцирования
имеем: 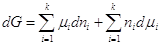 . .
Но 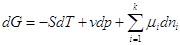 , а при p, T =const , а при p, T =const 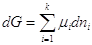 . .
Следовательно, 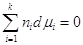 . .
Это уравнение называется уравнением Гиббса-Дюгема и широко применяется в
термодинамике растворов поскольку дает возможность рассчитать dμi i –ого компонента, если известны
изменения химических потенциалов всех остальных компанентов в
изобарно-изотермическом процессе. Для бинарного раствора 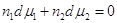 . .
Разделив на сумму п1
+п2, получим: 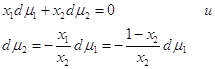 . .
7.4. Условия равновесия в многокомпонентных
гетерогенных системах.
Пусть р, Т = Const, тогда 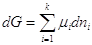 . Если в системе
имеются фазы (') и (''), то при переходе dni молей i –ого компонента из фазы (') в фазу ('') изменение
энергии Гиббса системы dG будет
складываться из изменении энергий Гиббса обеих фаз dG ' и dG '': . Если в системе
имеются фазы (') и (''), то при переходе dni молей i –ого компонента из фазы (') в фазу ('') изменение
энергии Гиббса системы dG будет
складываться из изменении энергий Гиббса обеих фаз dG ' и dG '': 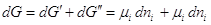 . .
Если система закрытая, то 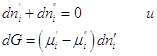 , а если она к тому же и равновесна, то dG = 0 и, следовательно, , а если она к тому же и равновесна, то dG = 0 и, следовательно, 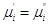 , т.е. химические
потенциалы данного компонента во всех фазах системы, находящейся в равновесии,
равны между собой. , т.е. химические
потенциалы данного компонента во всех фазах системы, находящейся в равновесии,
равны между собой.
Самопроизвольный неравновесный процесс может идти только в сторону
уменьшения энергии Гиббса системы dG < 0 (p, T = const).
Предположим, что 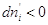 , т.е. фаза (')
теряет i –ый компонент, но , т.е. фаза (')
теряет i –ый компонент, но 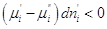 , значит , значит 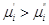 . .
Если же 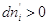 , тогда , тогда 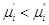 . Таким образом, компонент самопроизвольно переходит
из фазы, в которой его химический потенциал больше, в фазу, в которой его
химический потенциал меньше. . Таким образом, компонент самопроизвольно переходит
из фазы, в которой его химический потенциал больше, в фазу, в которой его
химический потенциал меньше.
Эти условия равновесия и
самопроизвольности процессов переноса вещества в многокомпонентных системах
являются обобщением таковых для однокомпонентных систем (см. гл. 6). Кроме
того, легко заметить, что химический потенциал чистого вещества равен его
мольной энергии Гиббса.
Глава 8. Термодинамика смесей идеальных газов.
8.1. Характеристические функции идеального газа.
Для адиабатического процесса в системе (Q = 0) мы можем записать ΔU= -A.
Если идеальный газ расширяется адиабатически от объема V и температуры T до бесконечно большого объема, то он
совершает работу:
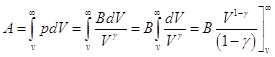 , ,
а поскольку  , то подстановка верхнего предела дает 0, подстановка
нижнего приводит к , то подстановка верхнего предела дает 0, подстановка
нижнего приводит к 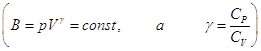 , ,
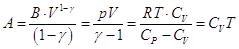 . .
Следовательно 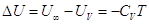 , а поскольку , а поскольку 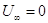 , то внутренняя энергия идеального
газа, имеющего данную температуру, равна U = CVT. , то внутренняя энергия идеального
газа, имеющего данную температуру, равна U = CVT.
Очевидно, поскольку для идеального газа dU = CV dT, то по первому закону для идеального
газа: dQ = CVdT + pdV.
Разделив правую и левую
часть на Т, получим 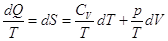 . .
Интегрирование дает 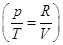 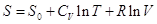 . .
Константа интегрирования S0 не зависит ни от температуры, ни от давления или объема. Как мы увидим
позднее для любого вещества в состоянии идеального газа в константу S0 в качестве характеристики вещества входит только его
мольная масса. Далее:
H
= U + pV = U
+ RT =
CVT +RT = CpT,
F
= U – TS = CVT – TS0 - CVT ln T –RT ln V,
G = H – TS = CpT – T( S0
+ R ln R ) – CpT ln T + RT ln p,
Легко видеть, что, вообще говоря,
F = F (T) –
RT ln V, G = G (T ) + RT
ln p,
где F (T) и G (T) - являются
функциями только температуры.
8.2. Химический потенциал газа в смеси идеальных
газов.
Смешение газов – самопроизвольный процесс, происходящий вследствие
диффузии. Дальтон (1801) отметил, что если взятые газы имеют одинаковую
температуру и давление, то в отсутствие химической реакции а) объем смеси равен
сумме объемов составляющих газов в) температура остается постоянной в течение
процесса. Т.е., если исходные объемы смешивающихся газов равны Vii , то общий объем смеси равен 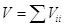 . Отметим, что Vii = ni Vi , где ni –число молей газа i, Vi – мольный объем его до процесса
смешения. Поскольку давление р в процессе смешения не меняется, то для
смеси . Отметим, что Vii = ni Vi , где ni –число молей газа i, Vi – мольный объем его до процесса
смешения. Поскольку давление р в процессе смешения не меняется, то для
смеси 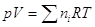 , а для i –
газа, занимающего объем смеси V,
парциальное давление pi: piV = niRT, следовательно , а для i –
газа, занимающего объем смеси V,
парциальное давление pi: piV = niRT, следовательно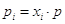 .
Обозначим индексом i
мольные свойства i – ого газа.
Тогда для смеси газов: .
Обозначим индексом i
мольные свойства i – ого газа.
Тогда для смеси газов:
 и, следовательно, и, следовательно,
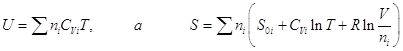 , ,
и энергия Гельмгольца смеси:
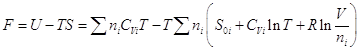 . .
Теперь становится возможным
вычислить химический потенциал i – ого газа: 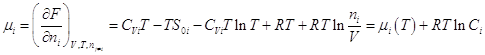 где где 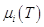 - функция только
температуры, а - функция только
температуры, а 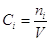 - концентрация i
- ого газа. Поскольку для смеси - концентрация i
- ого газа. Поскольку для смеси 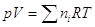 , то , то 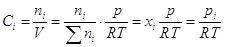 , ,
и химический потенциал i
–ого газа можно выразить через другие величины:
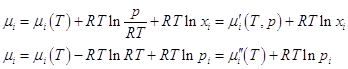 . .
Очевидно, что μi(T) – химический
потенциал газа, когда Ci = 1; μ' (T,p) – химический потенциал, когда xi = 1, т.е. это мольная энергия Гиббса
чистого газа i; μ''(T) – химический потенциал i - ого газа при pi = 1.
8.3. Энтропия смешения.
Энтропия смеси газов равна
(см. выше): 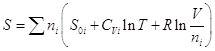 , но , но 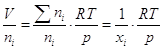 . .
Поскольку газ i
имел до смешения давление p
и объем Vii = nVi, имеем:
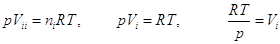 , и энтропия смеси тогда: , и энтропия смеси тогда: 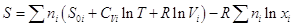 . .
Полином в скобках представляет собой мольную энтропию газа i до процесса смешения, поэтому сумма
есть не что иное, как энтропия системы до процесса смешения, следовательно,
изменение энтропии системы в результате смешения газов 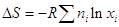 или в расчете на 1 моль
смеси: или в расчете на 1 моль
смеси:
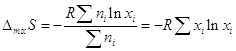 . .
Поскольку 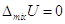 , то работа,
которую можно получить в результате обратимого процесса смешения газов: , то работа,
которую можно получить в результате обратимого процесса смешения газов: 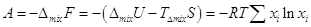 . .
Очевидно, что для разделения смеси газов на компоненты нужно затратить
работу 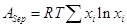 . .
Однако, это только теоретическая величина, практически затрачиваемая
работа будет намного больше, причем, чем меньше отличаются по свойствам
компоненты, тем большая потребуется работа.
Например, разделение изотопов урана осуществляют, используя гексафторид
урана. Природная смесь содержит 99,3 % U238 F6 и 0,7 % U235F6. Так вот
теоретически необходимо затратить 0,023 квт·час на выделение 1 кг U235F6,
практически приходится затрачивать 1,2·106 квт·час
или в 50·106 раз больше.
Мы видим также, что возрастание энтропии при смешении газов зависит
только от количества молей этих газов, но не зависит от их природы. В
предельном случае, когда смешивается один и тот же газ, разделенный сначала
перегородкой на две части, увеличения энтропии не должно быть, так как в этом
случае после удаления перегородки никакого термодинамического процесса в системе
не происходит. Таким образом, смешение идентичных газов нельзя рассматривать
как предельный случай смешения различных газов. Легко сообразить, что если
смешиваемые газы имели до смешения одинаковое давление р, то после
смешения они имеют парциальные давления pi <p, а если газы идентичны, то давление не меняется. При
переходе от образования смеси сколь угодно близких (разделимых) газов к смеси
одинаковых газов величина ΔmixS испытывает скачок. Это утверждение
получило название парадокса Гиббса.
|