Лабораторная работа: Исследование сегнетоэлектриков
Лабораторная работа: Исследование сегнетоэлектриков
Кафедра
конструирования и технологии электрической изоляции
Лабораторная
работа
Тема:
Исследование сегнетоэлектриков
2007
Цель работы: исследование основных
диэлектрических свойств сегнетоэлектриков в зависимости от напряженности
внешнего электрического поля и температуры осциллографическим методом.
Основные сведения из
теории
Сегнетоэлектриками
называется особая группа диэлектриков, которая ниже определенной температуры
или в некотором интервале температур обладает самопроизвольной (спонтанной)
поляризацией, т.е. находятся в поляризованном состоянии при отсутствии внешнего
электрического поля. Свое название они получили от сегнетовой соли, которая
явилась исторически первым сегнетоэлектриком.
Все известные
сегнетоэлектрики можно разделить на две основные группы: протонные
сегнетоэлектрики – вещества, содержащие водород (сегнетова соль, смешанные
кристаллы, родственные сегнетовой соли, дигидрофосфаты и дигидроарсенаты калия,
аммония и их дейтеро-замещенные соли) и вещества не содержащие водорода
(титанат бария, титанат свинца, родственные по структуре изоморфные смеси
титаната бария и другие соединения). По структуре, составу и свойствам эти две
группы значительно отличаются друг от друга. Первая группа сегнетоэлектриков
характеризуется сложной структурой, в них причиной возникновения спонтанной
поляризации принято считать протон. Эти кристаллы имеют спонтанную поляризацию
при низких температурах, отличаются хрупкостью, вследствие чего их практическое
применение затруднено и несколько ограничено.
Вторую группу составляют
беспротонные сегнетоэлектрики, отличительной особенностью структуры которых
является октаэдрическое окружение ионами кислорода меньшего по размерам
катиона. Это группу называют сегнетоэлектриками кислородно-октаэдрического
типа. Благодаря высоким электрическим характеристикам, простоте получения,
разнообразию свойств сегнетоэлектрики второй группы находят широкое применение
в различных областях техники.
Наличие спонтанной
поляризации определяет ряд особых свойств сегнетоэлектриков.
- Высокая диэлектрическая
проницаемость.
- Нелинейная зависимость
диэлектрической проницаемости от температуры и наличие точки Кюри (рис. 1).
- Нелинейная зависимость
вектора спонтанной поляризации и диэлектрической проницаемости от напряженности
внешнего электрического поля (рис. 2).
- Диэлектрический
гистерезис (рис. 3).
- Пьезоэффект.
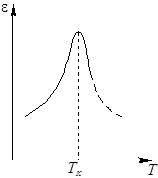
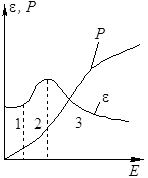
| Рис. 1.
Температурная зависимость диэлектрической проницаемости сегнетоэлектрика |
Рис. 2.
Зависимость поляризованности Р и диэлектрической проницаемости e сегнетоэлектрика от напряженности
внешнего электрического поля |
Из теорий
сегнетоэлектричества известны: термодинамическая – наиболее полная и строгая, и
теория локальных минимумов – менее строгая, но более наглядная.
Самопроизвольная
поляризация возникает в веществах, имеющих доменную структуру. Домен –
макроскопическая область, внутри которой электрические моменты отдельных частиц
равны по величине и расположены параллельно.
Согласно
термодинамической теории доменная структура в веществе возникает в том случае,
если при этом за счет упорядоченного расположения частиц обеспечивается минимум
полной энергии системы.
Для характеристики
степени упорядоченности частиц в сегнетоэлектрике Гинзбург выбрал величину
квадрата вектора поляризованности, так как величина свободной энергии не
зависит от его направления, и свободную энергию однодоменного изотропного
ненапряженного кристалла сегнетоэлектрика выразил в виде следующего ряда:
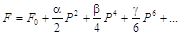 (1) (1)
где F0 – свободная
энергия кристалла в параэлектрической фазе;
P – модуль
вектора поляризованности;
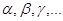 – коэффициенты разложения,
зависящие от свойств вещества, причем – коэффициенты разложения,
зависящие от свойств вещества, причем 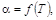
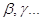 = const(T). = const(T).
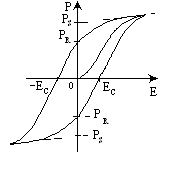 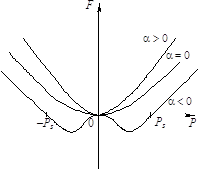
| Рис. 3. Петля
гистерезиса cегнето-электрика: PR – остаточная поляризован-ность; Ec –
коэрцитивное поле |
Рис. 4.
Зависимость свободной энергии F сегнетоэлектрика от поляризованности P
(PS – спонтанная поляризованность)
|
Из анализа соотношения
(1) следует, что устойчивое состояние спонтанной поляризации, соответствующее
минимуму свободной энергии:
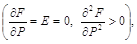
Возможно только после
того, как коэффициент 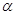 при переходе через некоторую
температуру T0 изменит знак и приобретет отрицательное значение (рис. 4): при переходе через некоторую
температуру T0 изменит знак и приобретет отрицательное значение (рис. 4):
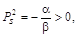 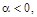 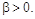 (2) (2)
Физическая картина
образования доменной структуры у сегнетоэлектриков кислородно-октаэдрического
типа (титаната бария) описывается теорией локальных минимумов, предложенных
Мэзоном и Маттиасом. Элементарная ячейка титаната бария представляет собой куб,
в вершинах которого находятся ионы Ba2+, в центрах – ионы O2–, внутри куба –
ион Ti4+ (рис. 5).
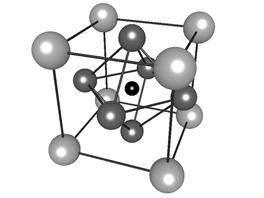
Рис. 5. Элементарная
ячейка титанита бария
Ион титана располагается
в пределах кислородного октаэдра, размеры которого много больше размеров иона
титана. Это дает возможность иону титану колебаться, смещаясь к одному из ионов
кислорода, и образовывать с ним частично ковалентную связь. Ковалентная связь
удерживает ион титана в смещенном состоянии. Поскольку в этом случае центры
положительного и отрицательного зарядов не совпадают, возникает электрический
момент элементарной ячейки. Этот момент действует на соседние ионы титана,
заставляя их смещаться в том же направлении. В результате появляется область
кристалла с одинаково ориентированными электрическими моментами отдельных
ячеек.
При кристаллизации
вещества все 6 возможных направлений смещения иона титана являются
равновероятными, поэтому возникающие домены взаимно уравновешиваются и кристалл
в целом не обладает электрическим моментом.
При наложении внешнего
электрического поля 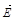 облегчается переброс ионов титана
к тем ионам кислорода, образование ковалентной связи с которыми приводит к
появлению момента, т. е. наблюдается рост доменов в направлении внешнего поля.
Этим объясняется возрастание спонтанной поляризации с ростом электрического
поля. Насыщение соответствует моменту полной ориентации всех доменов вдоль поля
(см. рис. 2). облегчается переброс ионов титана
к тем ионам кислорода, образование ковалентной связи с которыми приводит к
появлению момента, т. е. наблюдается рост доменов в направлении внешнего поля.
Этим объясняется возрастание спонтанной поляризации с ростом электрического
поля. Насыщение соответствует моменту полной ориентации всех доменов вдоль поля
(см. рис. 2).
С увеличением температуры
возрастает энергия теплового движения, благодаря чему облегчается разрушение
старой ковалентной связи и образование новой, при которой электрический момент
элементарной ячейки направлен вдоль поля. Таким образом, в случае
многодоменного кристалла нагрев облегчает переориентацию доменов и приводит к
увеличению спонтанной поляризации. При достижении определенной температуры
хаотическое движение иона титана становится настолько интенсивным, что он
колеблется внутри кислородного октаэдра, не создавая устойчивой ковалентной
связи ни с одним из ионов кислорода. Можно считать, что в среднем он находится
в центре октаэдра, и электрический момент элементарной ячейки становится равным
нулю. Спонтанная поляризация исчезает. В этом физический смысл температуры
Кюри.
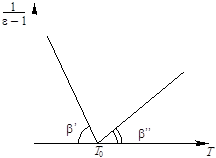
Рис. 6. Зависимость
диэлектрической проницаемости сегнетоэлектрика от температуры
Согласно
термодинамической теории сегнетоэлектричества диэлектрическая проницаемость при
воздействии внешнего электрического поля и температурах, близких к температуре
Кюри, изменяется следующим образом (рис. 6):
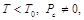
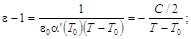 (3) (3)
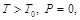
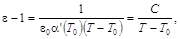 (4) (4)
где 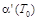 – производная от – производная от 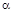 по по 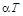 в точке Т =
Т0. в точке Т =
Т0.
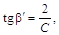 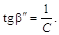
Термодинамическая теория
позволяет объяснить явление диэлектрического гистерезиса.
Расчетная часть
Начальные условия:
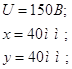
h - толщина
сегнетоэлектрика 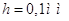
d – диаметр обкладки 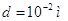
S - площадь
сегнетоэлектрика: 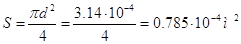
П - площадь петли
гистерезиса 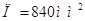 . .
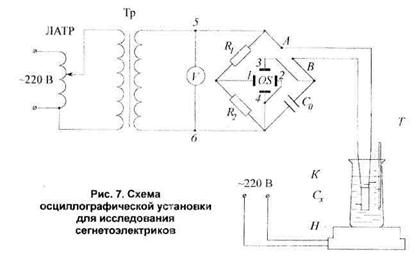
Подать напряжение 60 В на
образцовый конденсатор. На экране осциллографа будет видна наклонная прямая,
соответствующая зависимости заряда образцового конденсатора от приложенного
напряжения.
Определить отклонения X и
Y и вычислить:
а) масштаб по
горизонтальной оси электронно-лучевой трубки осциллографа:
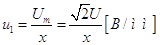 , ,
где 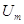 -амплитуда приложенного
напряжения; -амплитуда приложенного
напряжения;
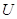 - показание вольтметра; - показание вольтметра;
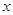 - отклонение от горизонтальной
оси, соответствующее амплитуде приложенного напряжения; - отклонение от горизонтальной
оси, соответствующее амплитуде приложенного напряжения;
б) масштаб по
вертикальной оси электронно-лучевой трубки осциллографа:
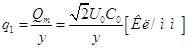 , ,
где 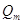 -заряд, соответствующий
амплитудному значению напряжения на обкладках образцового конденсатора -заряд, соответствующий
амплитудному значению напряжения на обкладках образцового конденсатора 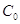 ; ;
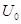 -напряжение на образцовом
конденсаторе, -напряжение на образцовом
конденсаторе,
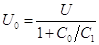 ; ;
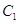 - ёмкость градуировочного
конденсатора - ёмкость градуировочного
конденсатора
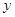 - отклонение от вертикальной оси. - отклонение от вертикальной оси.
в) диэлектрическая
проницаемость сегнетоэлектрика:
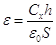 , ,
где 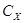 - ёмкость конденсатора
из сегнетоэлектрика, [Ф] - ёмкость конденсатора
из сегнетоэлектрика, [Ф]
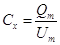 , ,
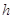 - толщина образца - толщина образца
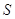 - площадь обкладок - площадь обкладок
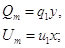
г) тангенс угла
диэлектрических потерь сегнетоэлектрика:
Диэлектрические потери в
общем случае выражаются уравнением
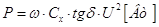 . .
Отсюда
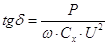
Мощность потерь
вычисляется по формуле
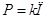 , ,
где 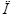 - площадь петли
гистерезиса, - площадь петли
гистерезиса, 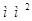 ; ;
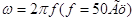 ; ;
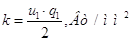
Результаты вычислений
записать в табл.1 и 2
Таблица 1
|
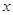 , ,
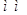
|
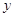 , ,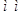
|
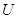 , ,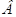
|
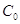 , ,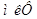
|
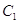 , ,
|
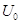 , ,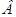
|
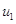 , ,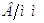
|
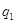 , ,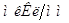
|
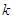 , ,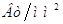
|
| 18 |
30 |
60 |
2 |
0,1 |
2,857 |
4,71 |
0,269 |
0,634 |
Таблица 2
При помощи ЛАТРа и
вольтметра изменять напряжение на сегнетоэлектрике от 150 В до 30 В с
интервалом 20 В, отсчитывая ординаты вершин кривой.
Таблица 3
|
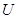
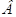
|
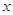
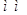
|
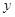
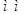
|
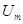
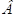
|

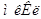
|
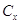
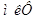
|
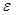
|
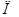
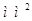
|
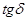
|
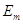
|
| 150 |
40 |
40 |
188,4 |
10,76 |
0,057 |
8200 |
840 |
8,26 |
1884 |
| 130 |
34 |
38 |
160,14 |
10,22 |
0,064 |
9210 |
760 |
6,66 |
1601,4 |
| 110 |
30 |
36 |
141,3 |
9,68 |
0,069 |
9930 |
670 |
5,45 |
1413 |
| 90 |
24 |
33 |
113,04 |
8,88 |
0,079 |
11370 |
600 |
4,26 |
1130,4 |
| 70 |
19 |
29 |
89,5 |
7,8 |
0,087 |
12520 |
430 |
2,77 |
895 |
| 50 |
13 |
22 |
61,2 |
5,92 |
0,097 |
13960 |
300 |
1,73 |
612 |
| 30 |
8 |
10 |
37,68 |
2,69 |
0,071 |
10220 |
130 |
1,03 |
376,8 |
График зависимости
диэлектрической проницаемости сегнетоэлектрика от напряженности электрического
поля в образце.
График зависимости
тангенса угла диэлектрических потерь от напряженности электрического поля в
образце.
Таблица 4
|
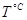
|
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
|
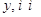
|
9 |
9 |
9 |
9 |
10 |
12 |
10 |
10 |
12 |
13 |
17 |
22 |
24 |
График зависимости ординаты
Y от температуры
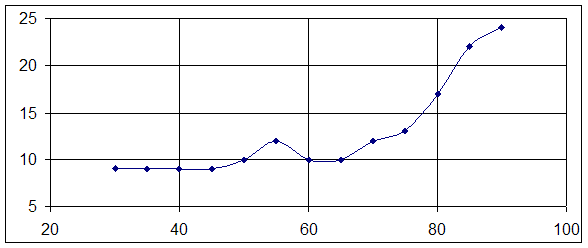
При температуре 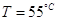 и и 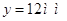 Y=12(мм)
появляется точка схожая с точкой Кюри(на этом участке она является точкой Кюри,
но с увеличением t возможно появление других точек Кюри). Y=12(мм)
появляется точка схожая с точкой Кюри(на этом участке она является точкой Кюри,
но с увеличением t возможно появление других точек Кюри).
Затем подключим
сегнетоэлектрик и подадим напряжение U=150 (В). При охлаждении фиксируем
значения Y и X через каждые 10 секунд. Рассчитываем оставшиеся неизвестные
величины и заносим их в таблицу.
Таблица 5
| t,
C |
X,
мм |
Y,
мм |
Um,
B |
Qm,
Кл
(10-6)
|
Cx,
Ф
(10-6)
|
|
П,
мм |
tg |
| 90 |
38 |
16 |
141,600 |
5,120 |
3,6 |
5,200 |
1840 |
0,0004538 |
| 80 |
37 |
17 |
113,100 |
5,440 |
4,8 |
6,917 |
1440 |
0,0002670 |
| 70 |
36 |
22 |
84,800 |
7,040 |
8,3 |
11,938 |
960 |
0,0001031 |
| 60 |
36 |
23 |
56,600 |
7,360 |
13,0 |
18,699 |
234 |
0,0000160 |
| 50 |
35 |
23 |
28,300 |
7,360 |
26,0 |
37,398 |
57 |
0,0000020 |
| 40 |
35 |
25 |
14,14 |
8,000 |
56,6 |
81,358 |
8 |
0,0000001 |
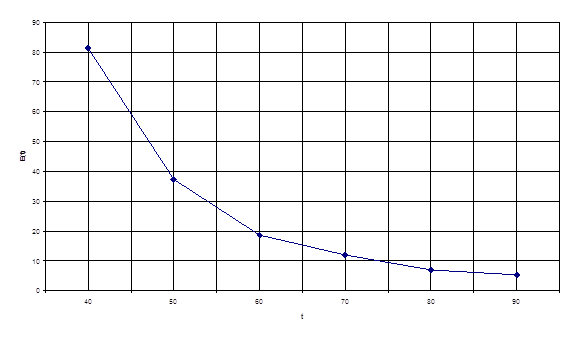 График
зависимости диэлектрической проницаемости сегнетоэлектрика от температуры График
зависимости диэлектрической проницаемости сегнетоэлектрика от температуры
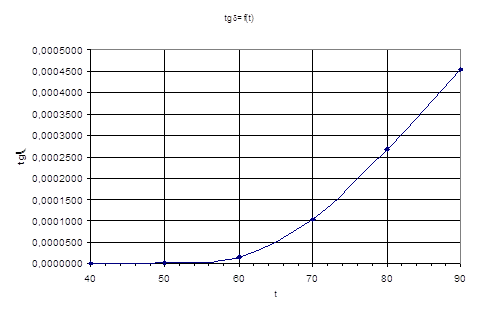 График
зависимости тангенса угла диэлектрических потерь от температуры График
зависимости тангенса угла диэлектрических потерь от температуры
Вывод: на графиках
наблюдается нелинейная зависимость тангенса угла диэлектрических потерь от
температуры и напряжённости внешнего электрического поля, что соответствует
свойствам сегнетоэлектриков.
|