Дипломная работа: Показательно-степенные уравнения и неравенства
Дипломная работа: Показательно-степенные уравнения и неравенства
белгородский
государственный университет
КАФЕДРА алгебры, теории чисел и
геометрии
Тема работы: Показательно-степенные уравнения и
неравенства.
Дипломная работа студента
физико-математического факультета
Научный руководитель:
______________________________
Рецензент : _______________________________
________________________
Белгород. 2006 г.
Содержание.
| Введение |
3 |
|
Тема
I.
|
Анализ
литературы по теме исследования. |
|
|
Тема
II.
|
Функции
и их свойства, используемые при решении показательно-степенных уравнений и
неравенств. |
|
|
I.1.
|
Степенная
функция и ее свойства. |
|
|
I.2.
|
Показательная
функция и ее свойства. |
|
|
Тема
III.
|
Решение
показательно-степенных уравнений, алгоритм и примеры. |
|
|
Тема
IV.
|
Решение
показательно-степенных неравенств, план решения и примеры. |
|
|
Тема
V.
|
Опыт
проведения занятий со школьниками по теме: «Решение показательно-степенных
уравнений и неравенств». |
|
|
|
V.1.
|
Обучающий
материал. |
|
|
|
V.2.
|
Задачи
для самостоятельного решения. |
|
|
Заключение.
|
Выводы
и предложения. |
|
|
Список
используемой литературы.
|
|
|
Приложения
|
|
Введение.
«…радость видеть и понимать…»
А.Эйнштейн.
В этой работе я попыталась передать
свой опыт работы учителем математики, передать хоть в какой-то степени свое
отношение к ее преподаванию — человеческому делу, в котором удивительным
образом переплетаются и математическая наука, и педагогика, и дидактика, и
психология, и даже философия.
Мне довелось
работать с малышами и выпускниками, с детьми, стоящими на полюсах
интеллектуального развития: теми, кто состоял на учете у психиатра и кто
действительно интересовался математикой
Мне довелось
решать множество методических задач. Я попытаюсь рассказать о тех из них,
которые мне удалось решить. Но еще больше — не удалось, да и в тех, что вроде
бы решены, появляются новые вопросы.
Но еще важнее
самого опыта — учительские размышления и сомнения: а почему он именно такой,
этот опыт?
И лето нынче на дворе иное, и
разворот образования стал поинтереснее. «Под юпитерами» нынче не поиски мифической
оптимальной системы обучения «всех и всему», а сам ребенок. Но тогда — с
необходимостью — и учитель.
В
школьном курсе алгебры и начал анализа, 10 – 11 класс, при сдаче ЕГЭ за курс
средней школы и на вступительных экзаменах в ВУЗы встречаются уравнения и
неравенства, содержащее неизвестное в основании и показатели степени – это
показательно-степенные уравнения и неравенства.
В
школе им мало уделяется внимания, в учебниках практически нет заданий на эту
тему. Однако, овладение методикой их решения, мне кажется, очень полезным: оно
повышает умственные и творческие способности учащихся, перед нами открываются
совершенно новые горизонты. При решении задач ученики приобретают первые навыки
исследовательской работы, обогащается их математическая культура, развиваются
способности к логическому мышлению. У школьников формируются такие качества
личности как целеустремленность, целеполагание, самостоятельность, которые
будут полезны им в дальнейшей жизни. А также происходит повторение, расширение
и глубокое усвоение учебного материала.
Работать
над данной темой дипломного исследования я начала еще с написания курсовой. В
ходе, которой я глубже изучила и проанализировала математическую литературу по
этой теме, выявила наиболее подходящий метод решения показательно-степенных
уравнений и неравенств.
Он
заключается в том, что помимо общепринятого подхода при решении
показательно-степенных уравнений (основание берется больше 0) и при решении тех
же неравенств (основание берется больше 1 или больше 0, но меньше 1),
рассматриваются еще и случаи, когда основания отрицательны, равны 0 и 1.
Анализ
письменных экзаменационных работ учащихся показывает, что неосвещенность
вопроса об отрицательном значении аргумента показательно-степенной функции в
школьных учебниках, вызывает у них ряд трудностей и ведет к появлению ошибок. А
также у них возникают проблемы на этапе систематизации полученных результатов,
где могут в силу перехода к уравнению – следствию или неравенству – следствию,
появиться посторонние корни. С целью устранения ошибок мы используем проверку
по исходному уравнению или неравенству и алгоритм решения
показательно-степенных уравнений, либо план решения показательно-степенных
неравенств.
Чтобы
учащиеся смогли успешно сдать выпускные и вступительные экзамены, я считаю,
необходимо уделять больше внимания решению показательно-степенных уравнений и
неравенств на учебных занятиях, либо дополнительно на факультативах и кружках.
Таким
образом тема, моей дипломной работы определена следующим образом:
«Показательно-степенные уравнения и неравенства».
Целями
настоящей работы являются:
1.
Проанализировать
литературу по данной теме.
2.
Дать
полный анализ решения показательно-степенных уравнений и неравенств.
3.
Привести
достаточное число примеров по данной теме разнообразных типов.
4.
Проверить
на урочных, факультативных и кружковых занятиях как будет восприниматься
предлагаемые приемы решения показательно-степенных уравнений и неравенств. Дать
соответствующие рекомендации к изучению этой темы.
Предметом
нашего исследования является разработка методики решения показательно-степенных
уравнений и неравенств.
Цель
и предмет исследования потребовали решения следующих задач:
1.
Изучить
литературу по теме: «Показательно-степенные уравнения и неравенства».
2.
Овладеть
методиками решения показательно-степенных уравнений и неравенств.
3.
Подобрать
обучающий материал и разработать систему упражнений разных уровней по теме:
«Решение показательно-степенных уравнений и неравенств».
В
ходе дипломного исследования было проанализировано более 20 работ, посвященных
применению различных методов решения показательно-степенных уравнений и
неравенств. Отсюда получаем.
План
дипломной работы:
Введение.
Глава
I. Анализ литературы по теме исследования.
Глава
II. Функции и их свойства, используемые при
решении показательно-степенных уравнений и неравенств.
II.1. Степенная функция и ее свойства.
II.2. Показательная функция и ее свойства.
Глава
III. Решение показательно-степенных уравнений,
алгоритм и примеры.
Глава
IV. Решение показательно-степенных неравенств,
план решения и примеры.
Глава
V. Опыт проведения занятий со школьниками по
данной теме.
1. Обучающий
материал.
2. Задачи
для самостоятельного решения.
Заключение.
Выводы и предложения.
Список
использованной литературы.
В
I главе проанализирована литература по теме:
«Решения показательно-степенных уравнений и неравенств».
В
II главе теоретические сведения о степенной и
показательной функциях и применение их свойств при решении
показательно-степенных уравнений и неравенств, выявляются недостатки в понимании
учащимися отрицательного аргумента показательно-степенной функции.
В
III главе «Решение показательно-степенных
уравнений, алгоритм и примеры» приведен полный анализ решения
показательно-степенных уравнений, рассмотрен алгоритм решения
показательно-степенных уравнений и примеры, и примеры в которых он применяется.
В
IV главе «Решение показательно-степенных
неравенств, план решения и примеры» приведен полный анализ решения
показательно-степенных неравенств и рассмотрен план решения
показательно-степенных неравенств и примеры, в которых он применяется.
В
V главе рассматривается методика обучения
учащихся решению показательно-степенных уравнений и неравенств, приведен
обучающий материал, разработана система заданий с учетом разного уровня
сложности, которая содержит в себе задания используемые на уроке, задания для
самостоятельного решения.
Глава II. Функции и их свойства, используемые при решении
показательно-степенных уравнений и неравенств.
Для решения
показательно-степенных уравнений и неравенств необходимо знать свойства
показательной и степенной функции и уметь ими пользоваться. В этой главе мы
рассмотрим данный вопрос.
II.1. Степенная функция и ее свойства.
 Степенная функция с натуральным показателем. Функция у = хn, где n — натуральное число, называется степенной функцией с натуральным
показателем. При n = 1 получаем функцию у = х, ее
свойства: Степенная функция с натуральным показателем. Функция у = хn, где n — натуральное число, называется степенной функцией с натуральным
показателем. При n = 1 получаем функцию у = х, ее
свойства:
Прямая
пропорциональность. Прямой пропорциональностью называется
функция, заданная формулой у = kxn, где число k называется коэффициентом
пропорциональности.
Перечислим свойства функции у
= kx.
1) Область определения функции — множество всех действительных чисел.
2) y = kx — нечетная функция (f( — х) = k ( — х)= — kx = -k(х)).
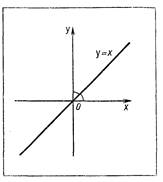 3) При k > 0 функция возрастает, а при k < 0 убывает на всей числовой
прямой. 3) При k > 0 функция возрастает, а при k < 0 убывает на всей числовой
прямой.
График (прямая) изображен на
рисунке II.1.
Рис. II.1.
При n=2 получаем функцию y = х2, ее свойства:
Функция у —х2.
Перечислим свойства функции у = х2.
1) Область определения функции — вся числовая прямая.
2) у = х2— четная функция (f( — х) = ( — x)2 = x2 = f (х)).
3) На промежутке [0; + οο) функция возрастает.
В самом деле,
если 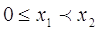 , то , то 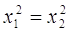 , а это и означает
возрастание функции. , а это и означает
возрастание функции.
4) На промежутке (—оо; 0] функция убывает.
В самом доле,
если 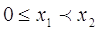 ,то — х1
> — х2 > 0, а потому ,то — х1
> — х2 > 0, а потому
(—х1)2>
( — х2)2, т. е. 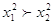 , а это и означает
убывание функции. , а это и означает
убывание функции.
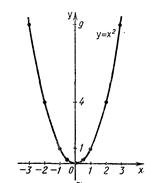 Графиком функции y=х2 является парабола.
Этот график изображен на рисунке II.2. Графиком функции y=х2 является парабола.
Этот график изображен на рисунке II.2.
Рис. II.2.
При n = 3 получаем функцию у = х3, ее
свойства:
1) Область определения функции — вся числовая прямая.
2) y = х3 — нечетная функция (f ( — х) = { — x)2 = — х3 = — f (x)).
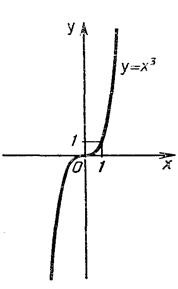 3) Функция y = x3 возрастает на всей
числовой прямой. График функции y = x3 изображен на рисунке. Он называется кубической параболой. 3) Функция y = x3 возрастает на всей
числовой прямой. График функции y = x3 изображен на рисунке. Он называется кубической параболой.
График (кубическая парабола)
изображен на рисунке II.3.
Рис. II.3.
Пусть n— произвольное четное натуральное
число, большее двух:
n = 4, 6, 8,... . В этом случае
функция у = хn обладает теми
же свойствами, что и функция у = х2. График такой
функции напоминает параболу у = х2, только ветви
графика при |n| >1 тем круче идут вверх, чем больше n, а при 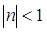 тем «теснее
прижимаются» к оси х, чем больше n. тем «теснее
прижимаются» к оси х, чем больше n.
Пусть n — произвольное нечетное число, большее трех: n = = 5, 7, 9, ... . В этом случае функция у = хn обладает теми же свойствами, что и функция у = х3.
График такой функции напоминает кубическую параболу (только ветви графика тем
круче идут вверх, вниз, чем больше n. Отметим также, что на промежутке (0; 1) график степенной функции у
= хn тем медленнее отдаляется от оси х с
ростом х, чем больше n.
Степенная функция
с целым отрицательным показателем. Рассмотрим
функцию у = х-n, где n — натуральное число. При n = 1 получаем у = х-n или у =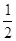 Свойства этой функции: Свойства этой функции:
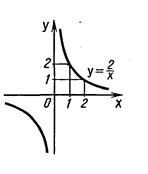 График (гипербола) изображен на рисунке II.4. График (гипербола) изображен на рисунке II.4.
Пусть n — нечетное число, большее единицы,
n = 3, 5, 7, ... . В этом случае
функция у = х-n обладает в основном теми же свойствами,
что и функция у =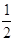 График
функции у = х-n (n = 3, 5, 7, ...) напоминает График
функции у = х-n (n = 3, 5, 7, ...) напоминает
Рис. II.4.
график функции у =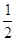 . Пусть n — четное число, например п = 2. Перечислим некоторые
свойства функции у = х-2, т. е. функции y = . Пусть n — четное число, например п = 2. Перечислим некоторые
свойства функции у = х-2, т. е. функции y = 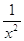 . .
1) Функция определена при всех х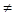 0. 0.
2) y = 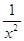 четная функция. четная функция.
3) y = убывает
на (0; +оо) и возрастает на (—оо;0).
Теми же свойствами обладают любые
функции вида y = х-n при четном n, большем
двух.
График функции у = 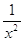 изображен на рисунке. Аналогичный вид имеет
график функции изображен на рисунке. Аналогичный вид имеет
график функции 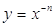 , если n = 4, 6, ... . , если n = 4, 6, ... .
Функции вида 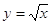 , ,
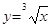 , , 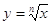 обладают теми же
свойствами, как и функция обладают теми же
свойствами, как и функция 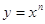 . .
Степенная функция
с положительным дробным показателем. Рассмотрим
функцию у = хr, где r
— положительная несократимая дробь. Перечислим некоторые
свойства этой функции.
1) Область определения — луч [0; + оо).
2) Функция ни четная, ни нечетная.
3) Функция у = хr возрастает на [0; +оо).
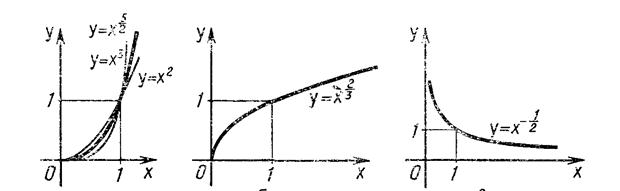
Рис. II.5.
На рисунке II.5. изображен график функции 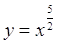 Он заключен между графиками
функций у = х2 и у = х3, заданных на промежутке [0; + оо). Он заключен между графиками
функций у = х2 и у = х3, заданных на промежутке [0; + оо).
Подобный вид имеет график любой
функции вида у = хr, где 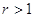 . .
На том же рисунке изображен график
функции 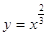 . Подобный вид имеет график любой степенной функции у = хr, где . Подобный вид имеет график любой степенной функции у = хr, где 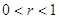 . .
Степенная функция с отрицательным
дробным показателем. Рассмотрим функцию у =
х-r, где r — положительная несократимая
дробь. Перечислим свойства этой функции.
1) Область определения — промежуток (0; + оо).
2) Функция ни четная, ни нечетная.
3) Функция у = х-r убывает на (0; +оо).
Построим для
примера график функции у — х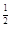 таблицу
значений функции: таблицу
значений функции:

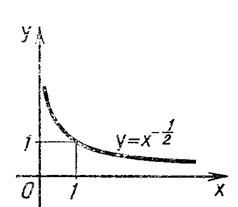 Нанесем полученные точки на координатную плоскость и соединим их плавной
кривой
(см. рис. II.6.). Нанесем полученные точки на координатную плоскость и соединим их плавной
кривой
(см. рис. II.6.).
Подобный вид имеет график любой функции
у = хr, где r — отрицательная дробь.
Рис. II.6.
II. 2. Показательная функция и ее свойства.
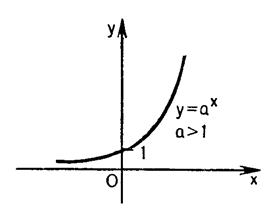 Функция, заданная формулой вида у = ах, где
а — некоторое положительное число, не равное единице, называется
показательной. Функция, заданная формулой вида у = ах, где
а — некоторое положительное число, не равное единице, называется
показательной.
1.Функция у = ах
при а>1 обладает следующими свойствами (см. рис. II.7.):
а) область определения —
множество всех действительных чисел;
б) множество значений — множество
всех положительных чисел;
Рис. II.7.
в) функция возрастает;
г) при х = 0
значение функции равно 1;
д) если x > 0, то аx > 1;
е) если х < 0,
то 0 < ах < 1.
3. Функция у = ах
при 0<а< 1 обладает следующими свойствами (см. рис. II.8.):
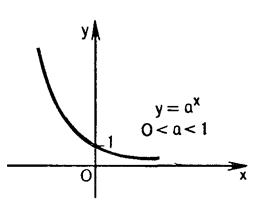 а) область определения D(f)=R; а) область определения D(f)=R;
б) множество значений E(f)=R+;
в) функция убывает;
г) при х = 0 значение функции
равно 1;
д) если х > 0,
то 0 < ах < 1;
е) если х < 0,
то ах > 1.
Рис. II.8.
Глава III. Решение показательно-степенных
уравнений, алгоритмы и примеры.
Так называются уравнения вида 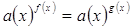 , где неизвестное
находится и в показателе и в основании степени. , где неизвестное
находится и в показателе и в основании степени.
Можно указать совершенно четкий
алгоритм решения уравнении вида 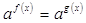 . Для
этого надо обратить внимание на то, что при а(х) не равном нулю, единице
и минус единице равенство степеней с одинаковыми основаниями (будь-то
положительными или отрицательными) возможно лишь при условии равенства
показателей То - есть все корни уравнения . Для
этого надо обратить внимание на то, что при а(х) не равном нулю, единице
и минус единице равенство степеней с одинаковыми основаниями (будь-то
положительными или отрицательными) возможно лишь при условии равенства
показателей То - есть все корни уравнения 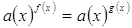 будут
корнями уравнения f(x) = g(x) Обратное же
утверждение неверно, при а(х) < 0 и дробных значениях f(x) и g(x) выражения а(х) f(x) и будут
корнями уравнения f(x) = g(x) Обратное же
утверждение неверно, при а(х) < 0 и дробных значениях f(x) и g(x) выражения а(х) f(x) и
а(х)g(x) теряют смысл. То - есть при
переходе от 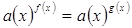 к f(x) = g(x) (при к f(x) = g(x) (при 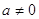 и и 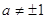 могут появиться
посторонние корни, которые нужно исключить проверкой по исходному уравнению. А
случаи а = 0, а = 1, а =-1 надо рассмотреть отдельно. могут появиться
посторонние корни, которые нужно исключить проверкой по исходному уравнению. А
случаи а = 0, а = 1, а =-1 надо рассмотреть отдельно.
Итак, для полного решения
уравнения 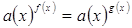 рассматриваем случаи: рассматриваем случаи:
1. а(х) = О . Если при значении х, удовлетворяющем этому уравнению, f(x) и g{x) будут
положительными числами, то это решение. В противном случае, нет
2. а(х) = 1. Корни этого уравнения являются корнями и исходного уравнения.
3. а(х) = -1. Если при значении х, удовлетворяющем этому уравнению, f(x) и g(x) являются
целыми числами одинаковой четности (либо оба четные, либо оба нечетные) , то
это решение. В противном случае, нет
4. При 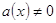 и и 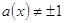 решаем уравнение f(x)= g(x) и подстановкой полученных результатов в исходное уравнение
отсекаем посторонние корни. решаем уравнение f(x)= g(x) и подстановкой полученных результатов в исходное уравнение
отсекаем посторонние корни.
Примеры
решения показательно-степенных уравнений.
Пример
№1.
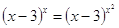
Решение
1) x – 3 =
0, x = 3. т.к. 3 > 0, и 32 > 0,
то x1 = 3 - это решение.
2) x
– 3 = 1,
x2
= 4.
3) x – 3 =
-1, x = 2. Оба показателя четные.
Это решение x3
= 1.
4) x – 3 ≠
0 и x ≠
± 1. x = x2, x = 0
или x = 1. При x = 0,
(-3)0 = (-3)0 –верно это решение x4 = 0.
При x = 1, (-2)1 = (-2)1
– верно это решение x5 = 1.
Ответ:
0, 1, 2, 3, 4.
Пример
№2.
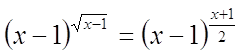
Решение
По
определению арифметического квадратного корня: x – 1 ≥
0, x ≥ 1.
1) x – 1 =
0 или x = 1, 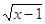 = 0, 00 это
не решение. = 0, 00 это
не решение.
2) x
– 1 = 1
x 1 = 2.
3) x – 1 =
-1 x 2 = 0
не подходит в ОДЗ.
4) 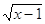 = = 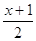
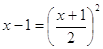 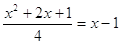
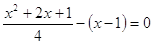
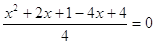
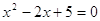
Д = (-2) – 4*1*5 = 4 – 20 = -16 –
корней нет.
Ответ:
2.
Пример
№3.
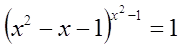
Решение
1)
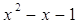 = 0 решения нет, т.к. 0
в любой степени не равен 1. = 0 решения нет, т.к. 0
в любой степени не равен 1.
2)
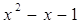 ≠ 0 т.е. ≠ 0 т.е. 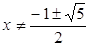 . Тогда можем записать: . Тогда можем записать:
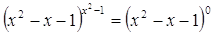
3)
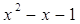 = 1. = 1. 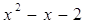 = 0 = 0
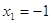 и и 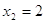
4)
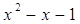 = -1 х = 0 или х = 1.
При х = 0 = -1 х = 0 или х = 1.
При х = 0 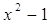 = -1. (-1)-1 ≠
(-1)0. Это не решение. При х = 1 (-1)0 = (-1)0.
Это решение х3 = 1. = -1. (-1)-1 ≠
(-1)0. Это не решение. При х = 1 (-1)0 = (-1)0.
Это решение х3 = 1.
5)
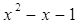 ≠ 0 и ≠ 0 и 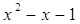 ≠ ±1 имеем ≠ ±1 имеем 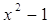 = 0, = 0, 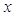 = -1 или = -1 или
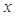 = 1. Эти корни уже
учтены. = 1. Эти корни уже
учтены.
Ответ:
-1, 1, 2.
Пример
№4.
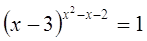
Решение
1)
При
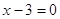 решений нет, т.к. 0 в любой
степени не равен 1. решений нет, т.к. 0 в любой
степени не равен 1.
при 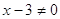 , , 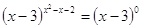
2)
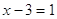 , , 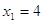 . .
3)
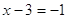 , , 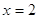 . .
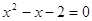 , (-1)0 = (-1)0
это решение. , (-1)0 = (-1)0
это решение.
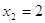 . .
4) 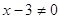 и и 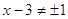
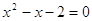
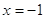 или или 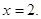
При 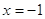 (-4)0
= 1 – верно. (-4)0
= 1 – верно. 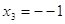
Ответ:
-1, 2, 4.
Пример
№5.
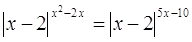
Решение
1)
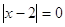 , , 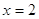 , , 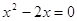 это не решение. это не решение.
2)
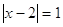 , , 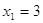 и и 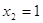 . .
3)
отрицательных значений основание не имеет. При 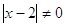 и и
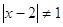 , , 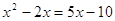 , , 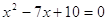 , ,
х
= 5, 315 = 315 – верно. х3 = 5,
х
= 2 – не является решением.
Ответ:
1,3,5.
Пример
№6
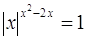
Решение
1)
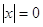 не дает решений, т.к. 0 ни
в какой степени не равен 1. не дает решений, т.к. 0 ни
в какой степени не равен 1.
2)
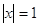 . . 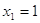 или или 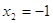 . .
3)
отрицательных значений 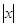 не имеет. не имеет.
4)
При 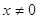 , , 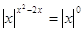
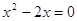 , т.к. , т.к. 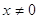 , то , то 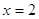 . Проверка 20 =
1 – верно. . Проверка 20 =
1 – верно. 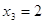
Ответ:
-1, 1, 2.
Пример
№7
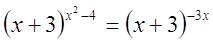
Решение
1)
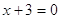 , , 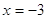 , , 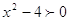 , , 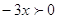 . Это решение . Это решение 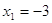 . .
2)
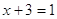 , , 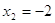 . .
3)
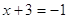 , , 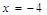 , , 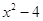 - четное и -3х – четное.
Это решение. х2 = -4. - четное и -3х – четное.
Это решение. х2 = -4.
4)
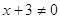 и и 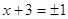 , , 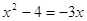 , , 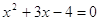 , , 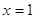 , 4-3 = 4-3
– верно. , 4-3 = 4-3
– верно. 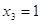 . .
Ответ:
-4, -3, -2, 1
Пример
№8
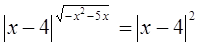
Решение
ОДЗ:
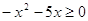 , , 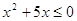
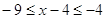 , , 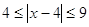 , ,
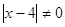 и и 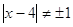
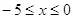
Все
решения принадлежат уравнению 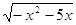 =2. =2.
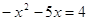 , , 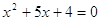 , , 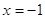 и и 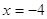 . Оба значения принадлежат
к ОДЗ. . Оба значения принадлежат
к ОДЗ.
Ответ:
-4, -1.
Пример
№9
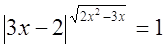
Решение
ОДЗ: 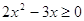 , , 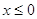 , , 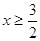 . .
1)
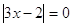 решений не имеет, т.к. 0 в
любой степени не равен 1. решений не имеет, т.к. 0 в
любой степени не равен 1.
При
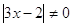 , , 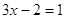 или или 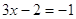 , ,
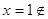 ОДЗ, ОДЗ, 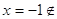 ОДЗ. ОДЗ.
Значит
все решения содержатся в уровнении 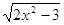 = 0, = 0, 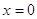 или или 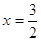 . .
Проверка:
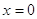 , 20 = 1 –
верно. , 20 = 1 –
верно.
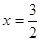 , , 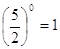 - верно. - верно.
Ответ:
0, 3/2.
Пример
№10
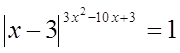
Решение
1)
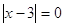 решений не дает, т.к. 0 в
любой степени не равен 1. решений не дает, т.к. 0 в
любой степени не равен 1.
2)
При 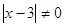 , , 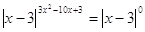 , , 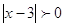 . Все решения принадлежат
уравнению . Все решения принадлежат
уравнению 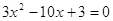 . . 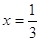 или или 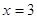 . .
3)
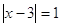 , , 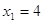 и и 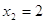 . .
Второе
решение не подходит, т.к 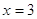 , , 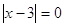 . А . А 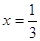 является решением является решением 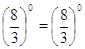
Ответ:
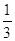 , 2, 4. , 2, 4.
Пример
№11
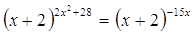
Решение
1)
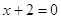 , , 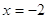 , , 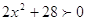 и и 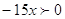 это решение это решение 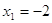 . .
2)
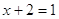 , , 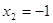 . .
3)
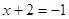 , , 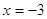 , , 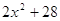 - четное, - четное, 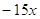 - нечетное. Это является
решением. - нечетное. Это является
решением.
4)
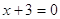 или или 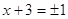 , , 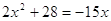 , , 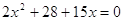 , , 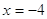 , , 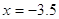 . .
Проверка:
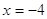 , , 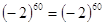 - верно. - верно.
Но
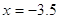 не является корнем! не является корнем!
Выражение
(-1,5)52,5, которое получается при проверке не имеет смысла, т.к.
степень отрицательно числа имеет смысл только для целых показателей. Равенство 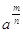 = = 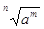 только для только для 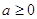 . Значит, отрицательное
число можно возводить только в степень с целым показателем. . Значит, отрицательное
число можно возводить только в степень с целым показателем.
Ответ:
-4, -2, -1.
Пример
№12
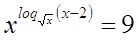
Решение
ОДЗ:
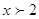 . Значит 0,1 и -1
отпадают. . Значит 0,1 и -1
отпадают.
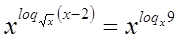 и все решения
содержатся в уравнении. и все решения
содержатся в уравнении.
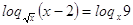
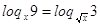 , , 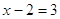 , , 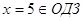
Ответ:
5.
Пример
№13
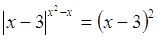
Решение
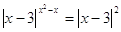
1)
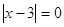 , , 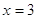 , , 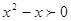 . Это решение . Это решение 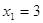 . .
2)
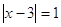 , , 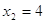 , , 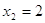 . .
3)
отрицательных значений 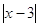 не имеет. не имеет.
При
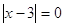 или или 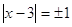 все решения в уравнении все решения в уравнении 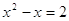 , , 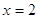 и и 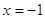 . .
При
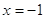 , , 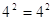 - верно. - верно. 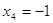 . .
Ответ:
-1, 2, 3, 4.
Пример
№14
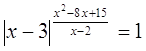
Решение
ОДЗ:
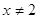
1)
При
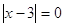 решений нет, т.к. 0 в
любой степени не равен 1. решений нет, т.к. 0 в
любой степени не равен 1.
При
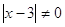
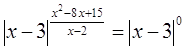
2)
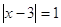 , , 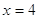 и и 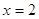 . . 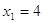 - решение, а - решение, а 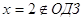 . .
3)
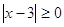 для всех для всех 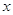 . При . При 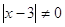 и и 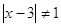 все решения содержатся в
уравнении все решения содержатся в
уравнении 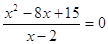 , , 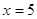 или или 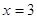 . При . При 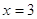 , , 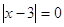 . .
При
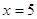 , , 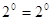 - верно. - верно. 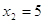 . .
Ответ:
4, 5.
Пример
№15.
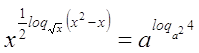 , , 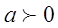
Решение
 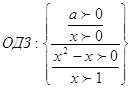
используя
свойства логарифма 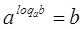 и и 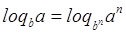 получили: получили:
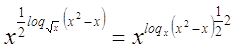 = = 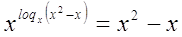
В
первой части уравнения выполнили преобразования
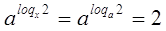 . Получили уравнение . Получили уравнение 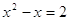 . Все решения содержатся в
уравнении. . Все решения содержатся в
уравнении.
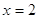 или или 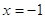 . . 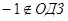
Ответ:
2.
Пример
№16
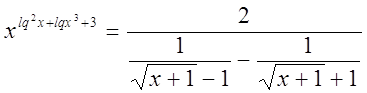
Решение
ОДЗ:
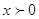
Преобразуем
знаменатель дроби в правой части уравнения
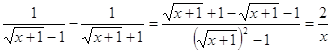 ; ; 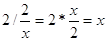 . .
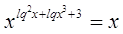 , , 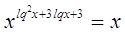 , где , где 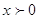
1)
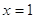 , , 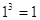 - верно. - верно.
2)
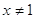 , , 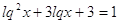
Пасть
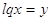 , тогда , тогда 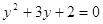
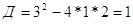
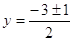 , , 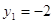 или или 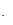 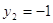 . .
Следовательно;
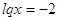 или или 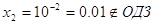 , , 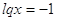 , , 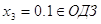 . .
Ответ:
1, 0,1, 0, 0,01.
Пример
№17
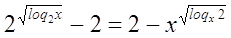
Решение
ОДЗ:
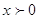 и и 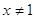
Выполним
преобразования.
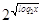 + +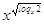 =
2+2 =
2+2
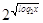 + +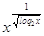 =
4 =
4
Пусть
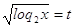 , а , а 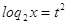 , , 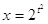
Следовательно,
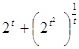 или или
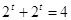 , , 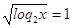
2*2t =
4 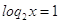
2t =
4/2 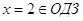
2t = 2
t = 1
Ответ:
2.
Пример
№18
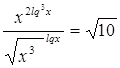
Решение
ОДЗ:
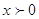
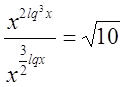 ; ; 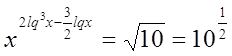
Прологарифмируем
обе части равенства:
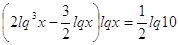
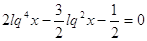 , где , где 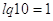 . .
Умножим
обе части уравнения на 2.
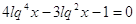
Пусть
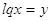 , тогда , тогда 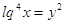
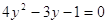
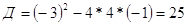
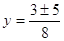 , , 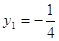 или или 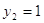
1)
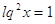 , , 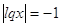
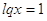 или или 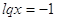
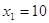 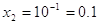
Ответ:
0.1, 10.
Пример
№19
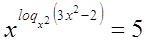
Решение
ОДЗ:
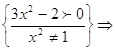 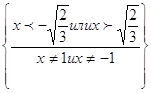
Обратите
внимание 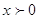 ниоткуда не следует!
Наоборот, из ОДЗ видно, что ниоткуда не следует!
Наоборот, из ОДЗ видно, что 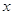 может
быть отрицательным! может
быть отрицательным!
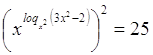
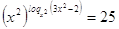 , , 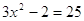
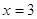 или или 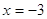
Оба
значения в ОДЗ.
Так
как возводили в квадрат, корни надо проверить.
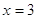 , , 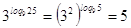 - верно. - верно.
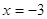 , , 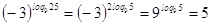 - верно. - верно.
Ответ:
-3, 3.
Пример
№20
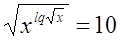
ОДЗ:
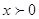
Возведем
обе части уравнения в квадрат (т.к. они положительны, то посторонние корни не
появляются)
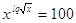 или или 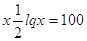
Прологарифмируем
по основанию 10.
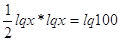
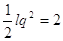 или или 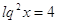
1) 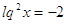 или или 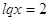
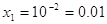 , , 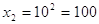
Ответ:
0.01, 100.
Пример
№21
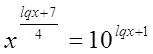
Решение
ОДЗ:
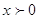
Прологарифмируем
по основанию 10.
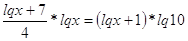 , где , где 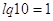 . .
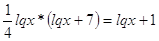
Пусть
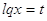 , тогда: , тогда:
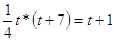 умножим на 4 умножим на 4
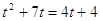
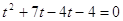 , , 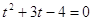
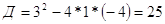
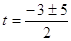 , , 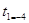 или или 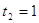
1)
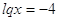
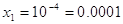
2)
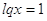
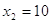
Ответ:
0,0001, 10.
Пример
№22
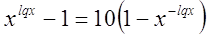
Решение
ОДЗ:
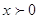
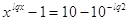
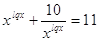
Заменим:
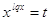 , получим: , получим:
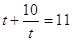 , где , где 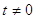 . .
Решаем
уравнение: 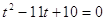
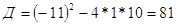
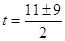 ; ; 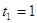 или или 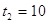
1)
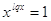 ; ; 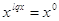 ; ; 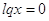 . . 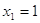 . .
2)
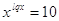 , , 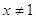 , , 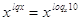 , , 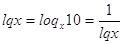 , , 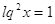 . .
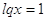 ; ; 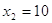 ; ; 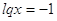 ; ; 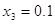 . .
Ответ:
0,1, 1, 10.
Пример
№23
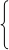 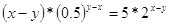
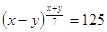
Решение
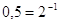 и и 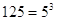
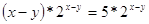 \
: \
: 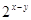
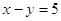
Подставим
во второе уравнение вместо 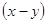 число
5, получим: число
5, получим:
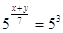
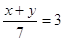 или или 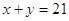
составляем
систему уравнений:
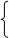 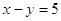
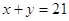
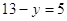
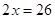
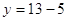
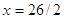
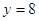
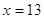
Ответ:
(13;8)
Пример
№24
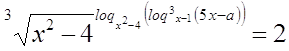
Решение
ОДЗ:
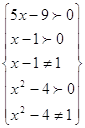 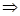 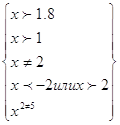 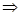 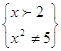
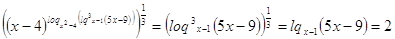 ; ; 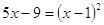
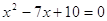 , ,
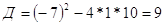
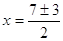 ; ; 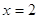 или или 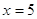
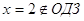 , , 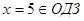 . .
Ответ:
5.
Пример
№25
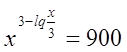
Решение
ОДЗ:
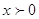
Прологарифмируем
правую и левую части данного уравнения по основанию 10:
Получим:
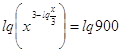 или или 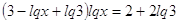
Обозначив
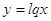 , перепишем записанное
уравнение в виде: , перепишем записанное
уравнение в виде:
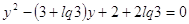 . .
Решая
его относительно 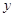 , находим , находим 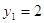 , , 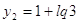 . .
Используя
обозначения 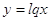 , из первого решения
квадратного уравнения имеем , из первого решения
квадратного уравнения имеем 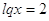 . Отсюда . Отсюда
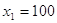 . Используя решение . Используя решение 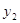 , получаем , получаем 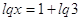 . Преобразуем правую часть
этого уравнения: . Преобразуем правую часть
этого уравнения:
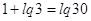 . Значит, . Значит, 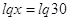 , т.е. , т.е. 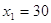 . .
Ответ:
30, 100.
Пример
№26
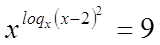
Решение
Так
как 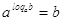 , то при , то при 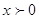 и и 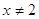 имеем равносильное
уравнение: имеем равносильное
уравнение:
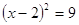 или или 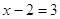
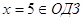 . .
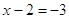 , , 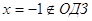
Ответ:
5.
Пример
№ 27
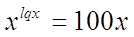
Решение
ОДЗ:
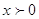
Так
как обе части уравнения положительны, то прологарифмируем по основанию 10:
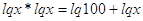
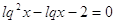
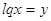 , , 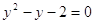
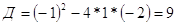
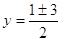 ; ; 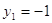 или или 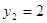
1)
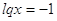 2) 2)
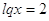
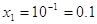 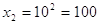
Ответ:
0.1, 100.
Пример
№28
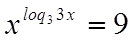
Решение
ОДЗ:
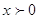
Так
как обе части уравнения положительны, то прологарифмируем по основанию 3:
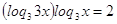
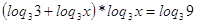
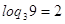 и и 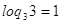 , поэтому , поэтому
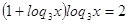
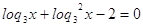
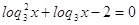
Пусть
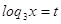 , тогда , тогда 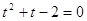
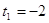 или или 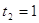 . .
1)
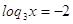
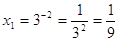 ; ;
2)
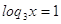
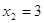
Ответ:
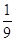 , 3. , 3.
Пример
№29
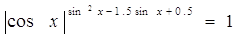
Решение
1)
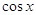 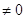 , т.к. 0 в любой степени не
равен 1. , т.к. 0 в любой степени не
равен 1.
2)
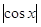 = 1, = 1, 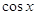 =1, =1, 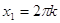 , , 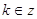 или или
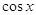 =-1, =-1, 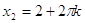 , , 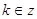 . .
Так
как 1 в любой степени равна 1, то это решения.
3)
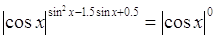 (т.к. (т.к. 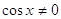 ) )
При
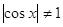 все решения принадлежат
уравнению все решения принадлежат
уравнению 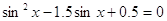 . . 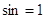 или или 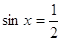 . .
При
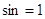  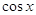 =
0, что не удовлетворяет уравнению =
0, что не удовлетворяет уравнению 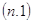
 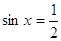 , , 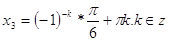
Ответ:
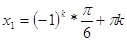 , , 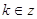 . .
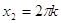 , , 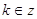 . .
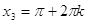 , , 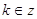 . .
Пример
№30
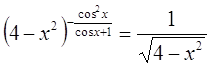
Решение
ОДЗ:
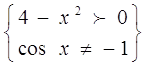 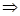 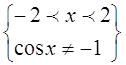
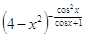 = = 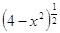
1)
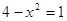 , , 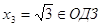 , , 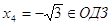 . .
2)
Так как 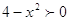 , то остальные решения
получаем из уравнения , то остальные решения
получаем из уравнения 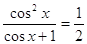 : Отсюда : Отсюда 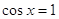 или или 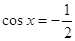 . . 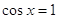 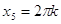 , , 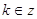 и и 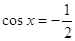  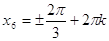 , , 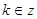 . .
Ответ:
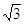 , - , -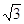 , , 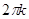 и и 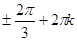 , , 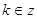 . .
Пример
№31
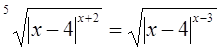
Решение
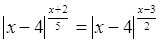
1) 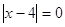 или или 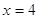 , ,
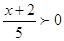 и и 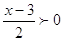 . Это
решение. . Это
решение. 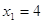 . .
2)
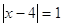 , , 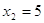 и и 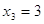
3)
Так как 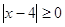 , то , то 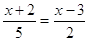 ; ;
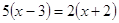 ; ;
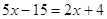
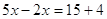
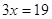
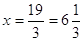 ; ; 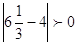 . Это решение. . Это решение.
Ответ:
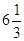 ; 5; 3; 4. ; 5; 3; 4.
Пример
№32
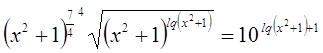
Решение
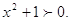 при всех при всех 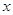
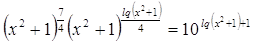
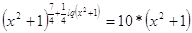
1)
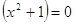 , , 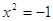 - решений нет. - решений нет.
2)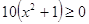 . Потому при . Потому при 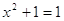 левая часть равна единице,
а правая нет. Это решение. левая часть равна единице,
а правая нет. Это решение.
3)
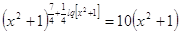 ; ;
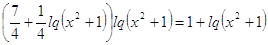 ; ;
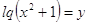 ; ;
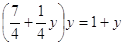 ; ;
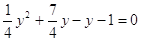 ; ;
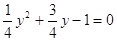 ; ;
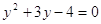 ; ;
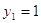 и и 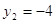 ; ;
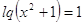 ; ; 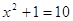 ; ;
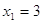 ; ; 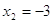 ; ;
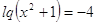 ; ;
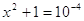 ; ;
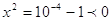 - решений нет. - решений нет.
Ответ:
-3, 3.
Пример
№33
Решить
графически уравнение:
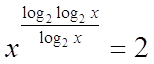
Решение
У
функции 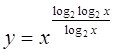 Д(y): x >
0 и log2 x >
0, т.е., Д(y): x >
0 и log2 x >
0, т.е.,
x > 1. обл. определения х > 1.
А
теперь:  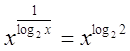 (формула
перехода к новому основанию и определение логарифма). (формула
перехода к новому основанию и определение логарифма).
Тогда
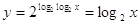 (определение логарифма: (определение логарифма: 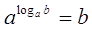 ). ).
Так,
что нужно только учитывать, что Д(у): x >
0.
Построим
график функции (рис III.1).
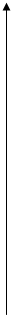
у

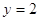
  2
2
1

0 1
4 х
Рис.
III.1.
Ответ:
(4; 2).
Пример
№34
Решить
систему уравнений:
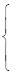 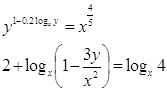
Решение:
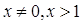
По
определению логарифма имеем:
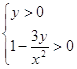 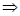 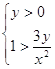 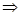 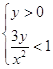 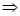 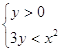 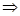 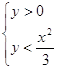 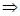 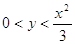 . .
Прологарифмируем
первое уравнение системы по основанию х.
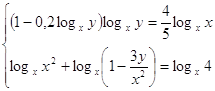 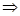 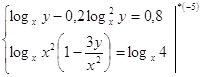 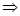 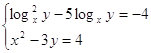 . .
Из
второго уравнения системы выразим у через х:
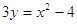 , , 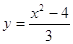
Тогда:
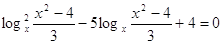
Пусть
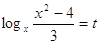 , , 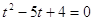 , Д =
(-5)2 -4*1*4 = 9, , Д =
(-5)2 -4*1*4 = 9, 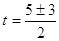 , , 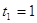 или или 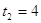 . .
1) 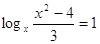 2) 2)
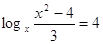
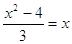
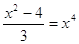
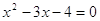
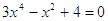
Д = (-3)2 –
4*1*(-4) = 25 пусть 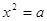 , тогда , тогда
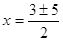
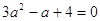
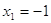 или или 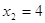 Д
= (-1)2 – 4*3*4 = -47<0 Д
= (-1)2 – 4*3*4 = -47<0
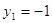 или или 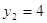 корней
нет корней
нет
(-1,-1) –
удовлетворяет ОДЗ
(4,4)
решение системы уравнений.
Ответ:
(4, 4).
Пример
№35
Решите
систему уравнений:
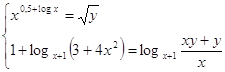
Решение.
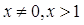
По
определению логарифма имеем:
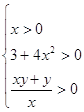 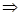 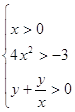 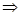 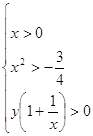
Основание
логарифма может быть:
1)
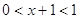 (дробное) (дробное)
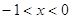
(-1, 0) – не удовлетворяет ОДЗ.
2)
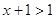
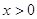
Выполним
преобразования:
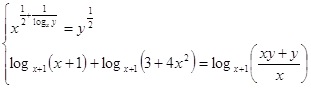
Прологарифмируем
первое уравнение системы по основанию х:
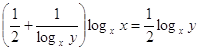 , ,
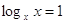 , , 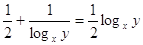 , ,
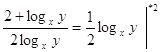
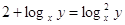 или или 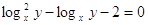
Пусть
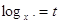 , тогда , тогда 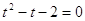
Д
= (-)2 -4*1*(-2) = 9
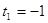 или или 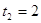
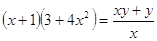
 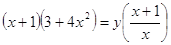 : (х+1) : (х+1)
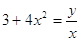
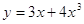 , где , где 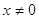
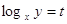 ; ;
1)
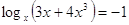
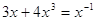 или или 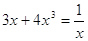
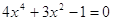
Решаем
биквадратное уравнение
Примем
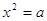 , тогда получим , тогда получим 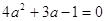
D = 32 – 4*1*(-4) = 25
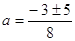 ; ; 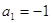 или или 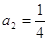
а)
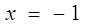
б)
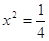 ; ; 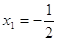 (не удовлетворяет ОДЗ) (не удовлетворяет ОДЗ)
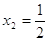
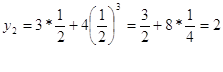
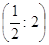 -
решение системы уравнений. -
решение системы уравнений.
2)
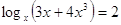
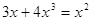
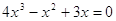
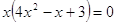
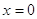 или или 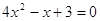
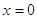 - (не удовлетворяет ОДЗ) - (не удовлетворяет ОДЗ)
D = (-1)2 -4*4*3 = -47 –
корней нет.
Ответ:
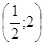 . [ ] . [ ]
Пример
№ 36
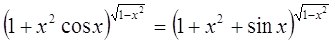
Решение
Для
любого х 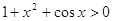 и и 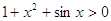 ОДЗ этого уравнения
состоит из всех х удовлетворяющих условию ОДЗ этого уравнения
состоит из всех х удовлетворяющих условию 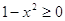 ,
т.е. ОДЗ есть множество всех х из промежутка ,
т.е. ОДЗ есть множество всех х из промежутка 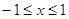 на этом множестве. Исходное
уравнение равносильно совокупности уравнений. на этом множестве. Исходное
уравнение равносильно совокупности уравнений.
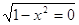 и
и 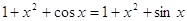
Решаем
ее.
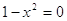
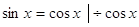
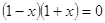
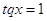
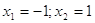
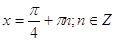
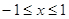 принадлежат принадлежат 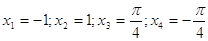 . Они и являются решениями
исходного уравнения. . Они и являются решениями
исходного уравнения.
Ответ:
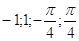 . .
Глава
IV. Решение
показательно-степенных неравенств, план решения и примеры.
Неравенства вида 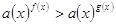 (или меньше) при а(х)>0
и (или меньше) при а(х)>0
и 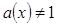 решаются на основании
свойств показательной функции: для 0 < а(х) < 1 при сравнении f(x) и g(x) знак неравенства меняется, а при а(х)
> 1 – сохраняется. решаются на основании
свойств показательной функции: для 0 < а(х) < 1 при сравнении f(x) и g(x) знак неравенства меняется, а при а(х)
> 1 – сохраняется.
Самый сложный случай при а(х)
< 0. Здесь можно дать только общее указание: определить, при
каких значениях х показатели f(x) и g(x) будут целыми числами, и выбрать из
них те, которые удовлетворяют условию
Наконец, если
исходное неравенство будет выполняться при а(х) = 0 или а(х) =
1 (например, когда неравенства нестрогие), то нужно рассмотреть и эти
случаи.
Пример 1.
Решить неравенство:
23x:+7 < 22x-1.
Решение.
Здесь основание степени
больше 1, поэтому, сравнивая показатели, запишем неравенство того же смысла: Зх
+ 7 < 2х - 1. Решив это неравенство, получим х < - 8.
Ответ: -8.
Пример 2.
Решить неравенство:
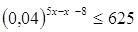
Решение.
Так как 625 = 252=
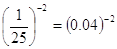 , то заданное неравенство
можно записать в виде , то заданное неравенство
можно записать в виде 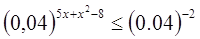
Так как 0
< 0,04 < 1, то, сравнивая показатели, запишем неравенство
противоположного смысла 5х - х2 - 8 = -2. Имеем последовательно
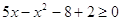 , ,
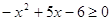 , ,
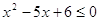 , ,
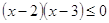 . .
Решив последнее неравенство, получим
2 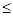 х х 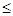 3. 3.
Таким образом множество решений
заданного неравенства есть отрезок [2; 3].
Ответ: [2; 3].
Пример 3.
Решим неравенство
0,57-Зх <
4.
Решение
Пользуясь тем, что
0,5 -2 = 4, перепишем заданное неравенство в виде
0,57-Зх <
0,5-2. Показательная функция y= 0,5x убывает (основание 0,5 меньше
1). Поэтому данное неравенство равносильно неравенству 7 – Зх > - 2, откуда
х < 3.
Ответ: ( — оо ; 3).
Пример 4.
Решим неравенство
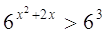
Показательная функция y = 6x возрастает. Поэтому данное
неравенство равносильно неравенству х2 + 2x > 3, решая которое, получим: (-оо; -3)
и (1; оо).
Ответ: (-оо; -3) и (1; оо).
Пример 5.
Решим неравенство:
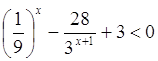
Сделаем замену 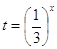 , тогда , тогда 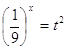 и неравенство перепишется в
виде и неравенство перепишется в
виде 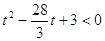 , откуда , откуда 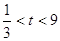 . Следовательно,
решением данного неравенства являются числа х, удовлетворяющие
неравенствам . Следовательно,
решением данного неравенства являются числа х, удовлетворяющие
неравенствам 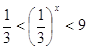 , и только такие числа. Но , и только такие числа. Но 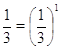 , , 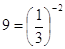 , а функция , а функция 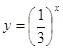 убывает, убывает,
поскольку 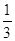 < 1. Поэтому решением
неравенств < 1. Поэтому решением
неравенств 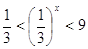 будут числа х, удовлетворяющие
неравенствам - 2 < х < 1. будут числа х, удовлетворяющие
неравенствам - 2 < х < 1.
Ответ: ( - 2; 1).
Пример 6.
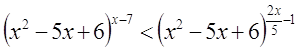
Решение
1) 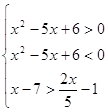 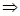 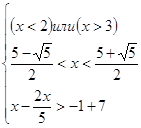 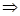
  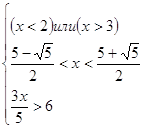 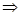 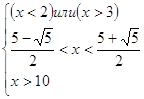
    
  
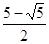 2 3 2 3  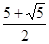 10 10
Изобразим на числовом луче
Должны выполняться все три неравенства,
т.к. это система. Но при 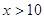 взятое
не выполняется. Решений нет. взятое
не выполняется. Решений нет.
2) 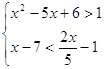 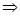 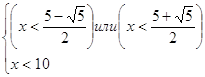
 Изобразим на числовом луче Изобразим на числовом луче

    
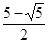 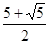 10 10
Если 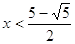 ,
то ,
то 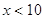
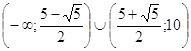 -решение
системы неравенств. -решение
системы неравенств.
Остальные случаи не дают решений, т.к. 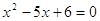 или 1 не
удовлетворяют условию, а при или 1 не
удовлетворяют условию, а при 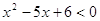 т.е. т.е. 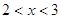 получаем
отрицательные числа с дробными показателями степени. получаем
отрицательные числа с дробными показателями степени.
Ответ: 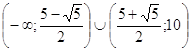
Пример 7
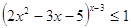
Решение
При 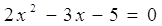 , х
= 2,5 или х = -1 , х
= 2,5 или х = -1
При 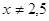 или или 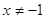 можно записать можно записать 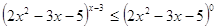 . .
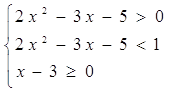 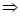 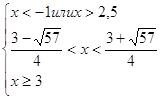
При 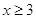 второе неравенство не
выполняется. Система решений не имеет. второе неравенство не
выполняется. Система решений не имеет.
Изобразим на числовом луче решение системы
неравенств
  
       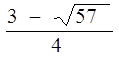 -1 2,5 -1 2,5
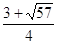 3 3
Система не имеет решений.
2)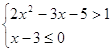 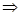 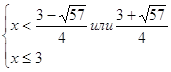
Изобразим на числовом луче решение системы неравенств
    
 
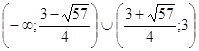 решение системы неравенств. решение системы неравенств.
3) 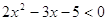 , , 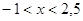 - выражение - выражение
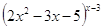 имеет
смысл тогда, когда х – 3 – целое число, чтобы показатель х – 3
был целым числом. Таким образом х – целое число в промежутке (-1; 2,5)
т.е. х может принимать значения 0,1,2. имеет
смысл тогда, когда х – 3 – целое число, чтобы показатель х – 3
был целым числом. Таким образом х – целое число в промежутке (-1; 2,5)
т.е. х может принимать значения 0,1,2.
Проверка:
При 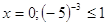 -
верно. -
верно.
При 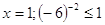 -
верно. -
верно.
При 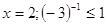 -
верно. -
верно.
4) 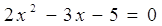 , х2
= 2,5 и х1 = -1 , х2
= 2,5 и х1 = -1
При х = -1 – не имеет смысла
выражение 0-4.
При х = 2,5, 02,5 – не
имеет смысла.
5) 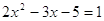
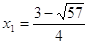 ; ; 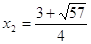
При 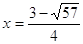 ; ;
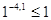 - верно. - верно.
При 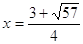 ; ;
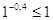 - верно. - верно.
Ответ: 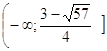 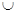 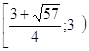 или или 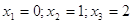 . .
Глава
V. Опыт проведения занятий со
школьниками
по
данной теме.
Анализируя
опыт проведения занятий по решению показательно-степенных уравнений и
неравенств с учащимися в старших классах я пришла к выводу, что недостаточно
времени уделяется на решения заданий и упражнений по данной теме. Всего в
школьном курсе на изучение математики отводится 850 часов, из них на решение
всех уравнений и неравенств всего лишь 12% учебного времени, а на решение
показательно-степенных уравнений и неравенств вообще ничтожное количество
часов. Однако, используя факультативные занятия в старших классах, кружковую
работу, элективные курсы можно значительно увеличить возможность учащихся
реализовать себя, усилить их подготовку к выпускным и вступительным экзаменам.
Проводя
занятия с учащимися я стараюсь больше внимания уделять решению конкретных
заданий и упражнений, на основе чего строю алгоритм решения и создаю модель
решения заданий одного вида или похожих между собой
Задачи
для самостоятельного решения.
Решить
уравнения.
1.
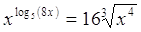 Ответ: Ответ:
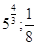 . .
2.
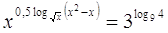 Ответ:
2. Ответ:
2.
3.
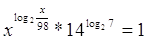 Ответ:
7; 14. Ответ:
7; 14.
4.
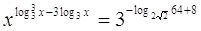 Ответ: Ответ:
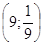 . .
5.
Найдите произведение корней уравнения
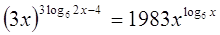 Ответ: Ответ:
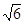 . .
6.
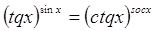 Ответ: Ответ:
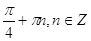 . .
7.
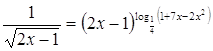 Ответ: Ответ:
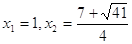 . .
8.
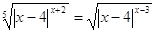 Ответ: Ответ:
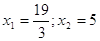 . .
9.
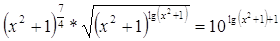 Ответ: Ответ: 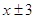
10.
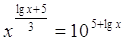 Ответ: Ответ:
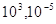 . .
11.
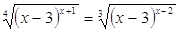 Ответ:
2; 3; 4; 11. Ответ:
2; 3; 4; 11.
12.
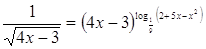 Ответ: Ответ:
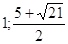 . .
13.
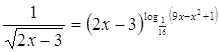 Ответ: Ответ:
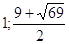 . .
14.
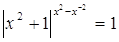 Ответ:
-2; 0; 2. Ответ:
-2; 0; 2.
15.
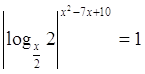 Ответ:
1; 4; 5. Ответ:
1; 4; 5.
16.
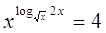 Ответ:
нет решений. Ответ:
нет решений.
17.
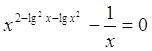 Ответ:
1; 10; 10-3. Ответ:
1; 10; 10-3.
18.
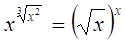 Ответ:
1; 8. Ответ:
1; 8.
19.
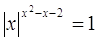 Ответ:
-1; 1; 2. Ответ:
-1; 1; 2.
20.
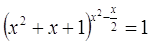 Ответ: Ответ:
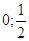 . .
21.
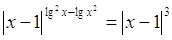 Ответ:
2; 10-1; 10-3. Ответ:
2; 10-1; 10-3.
22.
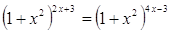 Ответ:
0; 3. Ответ:
0; 3.
23.
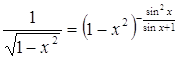 Ответ:
0. Ответ:
0.
24.
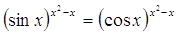 Ответ: Ответ:
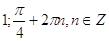 . .
25.
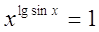 Ответ: Ответ:
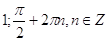 . .
26.
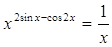
Ответ:
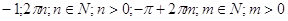 . .
27.
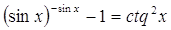 Ответ: Ответ:
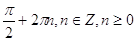 . .
28.
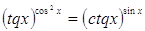
Ответ:
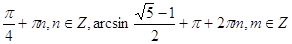 . .
29.
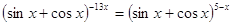 Ответ: Ответ: 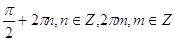 . .
30.
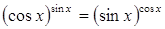 Ответ: Ответ:
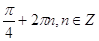 . .
31.
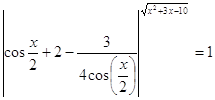
Ответ: 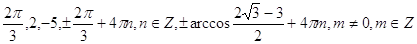 . .
32.
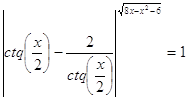
Ответ: 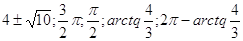 . .
33.
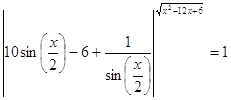
Ответ:
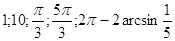 . .
34.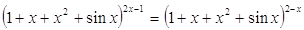 Ответ: 0; 1. Ответ: 0; 1.
35.
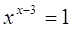 Ответ:
1; 3. Ответ:
1; 3.
36.
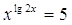 Ответ:
0; 1; 5. Ответ:
0; 1; 5.
37.
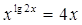 Ответ:
0; 5; 4. Ответ:
0; 5; 4.
38.
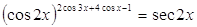
Ответ:
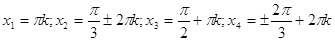 . .
39.
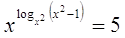 Ответ: Ответ: 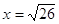 . .
40.
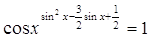 Ответ: Ответ: 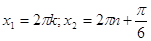 . .
41.
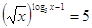 Ответ: Ответ:
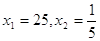 . .
42.
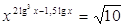 Ответ: Ответ: 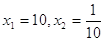 . .
43.
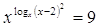 Ответ:
1; 0,1; 0,01. Ответ:
1; 0,1; 0,01.
44.
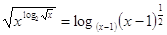
45.
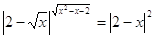 Ответ: -2;
-1; 3. Ответ: -2;
-1; 3.
46.
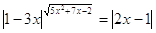 Ответ: -2;
0,6. Ответ: -2;
0,6.
47.
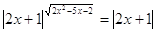 Ответ: Ответ: 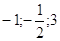 . .
48.
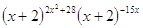 Ответ: -4;
-3,5; -2; -1. Ответ: -4;
-3,5; -2; -1.
49.
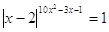 Ответ:
-0,2; 0,5; 1; 3. Ответ:
-0,2; 0,5; 1; 3.
50.
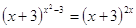 Ответ:
-2; 0,6. Ответ:
-2; 0,6.
Решить
системы уравнений
1.
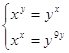 Ответ: Ответ:
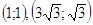 . .
2.
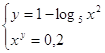 Ответ:
(5;-1). Ответ:
(5;-1).
3.
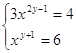 Ответ: Ответ:
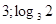 . .
4.
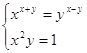 Ответ: Ответ:
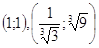 . .
5.
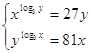 Ответ: Ответ:
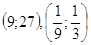 . .
6.
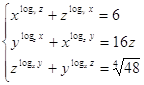 Ответ: Ответ: 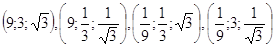 . .
7.
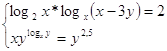 Ответ: Ответ: 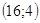 . .
8.
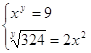 Ответ: Ответ:
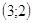 . .
9.
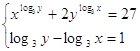 Ответ: Ответ: 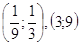 . .
10.
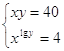 Ответ: Ответ:
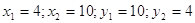 . .
11.
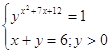
Ответ:
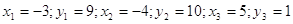 . .
12.
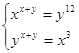 Ответ: Ответ:
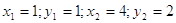 . .
13.
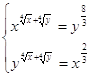
Ответ:
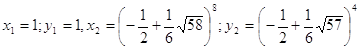 . .
14.
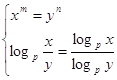
15.
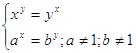
16.
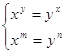
17.
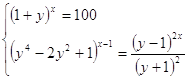
Ответ:
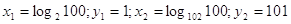 . .
18.
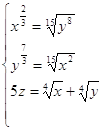
Ответ:
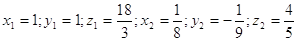 . .
19.
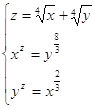
Ответ:
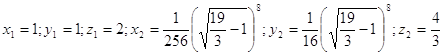 . .
20.
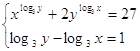 Ответ: Ответ: 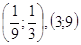 . .
21.
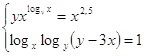 Ответ: Ответ: 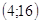 . .
22.
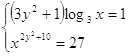 Ответ: Ответ: 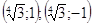 . .
23.
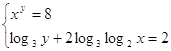 Ответ: Ответ: 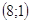 . .
Решить
неравенства.
1. 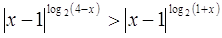
Ответ:
если 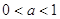 , то , то 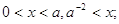 если если 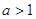 то то 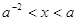 . .
2.
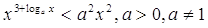 Ответ: Ответ: 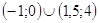 . .
3.
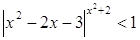 Ответ: Ответ: 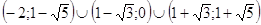 . .
4.
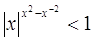 Ответ: Ответ:
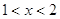 . .
5.
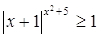 Ответ: Ответ:
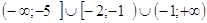 . .
6.
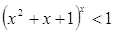 Ответ: Ответ:
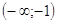 . .
7.
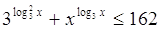 Ответ: Ответ: 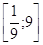 . .
8.
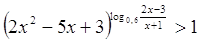 Ответ: Ответ: 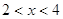 . .
9.
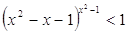 Ответ: Ответ:
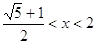 . .
10.
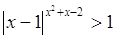 Ответ: Ответ: 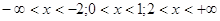 . .
11.
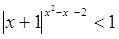 Ответ: Ответ: 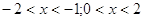 . .
12.
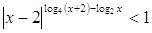 Ответ: Ответ: 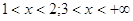 . .
13.
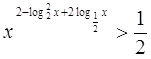 Ответ: Ответ: 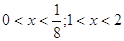 . .
14.
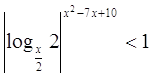 Ответ: Ответ: 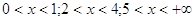 . .
15.
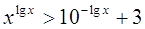 Ответ: Ответ: 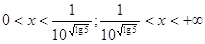 . .
16.
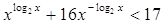 Ответ: Ответ: 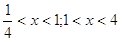 . .
17.
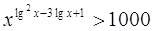 Ответ: Ответ: 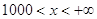 . .
18.
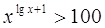 Ответ: Ответ: 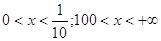 . .
19.
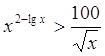 Ответ: Ответ: 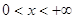 . .
20.
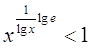 Ответ: Ответ: 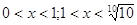 . .
21.
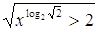 Ответ: Ответ: 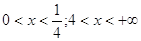 . .
Заключение.
Подводя
итоги данного дипломного исследования, можно сделать следующие выводы:
1.
Показательно-степенные
уравнения и неравенства представляют интерес для их изучения и использования в
курсах школьной математики и элементарной математики в ВУЗе. Между тем, почти
во всех пособиях они, если и рассматриваются, то не полно или не точно.
2.
Для
этого вида уравнений и неравенств может быть предложен алгоритм решения.
Наибольшие трудности могут встретиться при решении показательно-степенных
уравнений и неравенств в случае, когда основание степени отрицательно.
3.
Проведенные
по теме: «Показательно-степенные уравнения и неравенства» на уроках и
факультативных занятия в школе показали доступность этой темы для учеников,
интересующихся математикой. Для таких занятий изготовлен задачник, содержащий
более 70 показательно-степенных уравнений и неравенств.
Мое
предложение – больше уделять времени решению показательно-степенных уравнений и
неравенств, т.к. это поможет учащимся успешно сдать ЕГЭ и вступительные
экзамены в ВУЗы.
Материал,
приведенный в данной работе может служить методическим пособием в работе с
учащимися на уроках и факультативах.
Список
используемой литературы.
1.
Авербух
Б.Г., Рубинштейн А.И. Об определении степени и решении уравнений и неравенств,
содержащих показательно степенную функцию.//Математика в школе. –
1996.-№2.-с.29-33.
2.
Алгебра
и начала анализа: Учебник для 10-11 классов общеобразовательных учреждений:
Колмагоров А.Н., Абрамов А.М., Дудинцын Ю.П. и др.; Под редакцией Колмагорова
А.Н. – 12-е изд. – М.: Просвещение, 2002.
3.
Белоненко
Т.В., Васильев А.Е., Васильева Н.И., Крымская .Д. Сборник конкурсных задач по
математике. – СПб.: Спецлитература, 1997.
4.
Василенко
Ю.К. Тождества, уравнения, неравенства: Пособие для повышения квалификации
учителей математики. – Белаидит. Белгород, 2003.
5.
Василюк
Л.И., Куваева Л.А. Математика для абитуриентов: Справочник в экзаменационных
вопросах и ответах. – Мн. Амалфея, 1999.
6.
Давыденко
И.О. Пособие по математике. Для поступающих в высшие учебные заведения (с
анализом ошибок абитуриентов).- 2-е изд. – Томск,из-во Томского университета,
1973.
7.
Дорофеев
Г.В., Потапов М.К., Розов Н.Х. Математика для поступающих в ВУЗы. – М.: Дрофа,
2000.
8.
Дудинцын
Ю.П., Смирнова В.К. Содержание и анализ письменных экзаменационных работ по
алгебре и началам анализа: Пособие для учителя. – М.: Просвещение, 1995.
9.
Единый
государственный экзамен: Математика: Контрольно-измерительные материалы./
Денищева Л.О., Бойченко Е.М., Глазков6 под редакцией Ковалевой Г.С; М-во
образования Российской Федерацию – М.: Просвещение, 2003.
10.
Крамор
В.С. Повторяем и систематизируем школьный курс алгебры и начал анализа. – 2-е
изд. - М.: Просвещение, 1993.
11.
Кутасов
А.Д., Пиголкина Т.С., Чехлов В.И., Яковлева Т.Х.; под редакцией Яковлева Г.Н..
Пособие по математике для поступающих в ВУЗы.- 2-е изд.- М.: Наука, 1985.
12.
Математика.
Методические указания по подготовке к вступительным экзаменам./ СПбГИТМО. –
СПб., 2000.
13.
Нараленков
М.И. Вступительные экзамены по математике. Алгебра: как решать задачи:
Учебно-практическое пособие. – М.: Экзамен, 2003.
14.
Норин
А.В. Сборник задач по математике для поступающих в ВУЗы: Учебное пособие. –
Спб.: Питер, 2003.
15.
Потапов
М.К., Олейник С.Н., Нестеренко Ю.В. Конкурсные задачи по математике: Справочное
пособие. – 2-е изд. – М.: Физмалит, 2001.
16.
Потапов
М.К., Александров А.В., Пасиченко П.И. Алгебра и начала анализа. Современный
курс для поступающих в ВУЗы. – М.: Экзамен, 1998.
17.
Сборник
задач по математике для поступающих в ВУЗы./ Под ред. Проф. Прилепко А.И. – М.:
Высшая школа, 1983.
18.
Симонов
А.Я., Бакаев Д.С., Элельман А.Г. Система тренировочных задач и упражнений по
математике. – М.: Просвещение, 1991.
19.
Сканави
М.И. Сборник задач по математике для поступающих в ВУЗы. - М.: Просвещение,
1988.
20.
Цыпкин
А.Г., Пинский А.И. Справочник пособие по методам решения задач по математике
для средней школы. – М.: Наука. ГРФМЛ, 1984.
21.
Черкасов
О.Ю., Якушев А.Г. Математика. Интенсивный курс подготовки к экзаменам. – М.:
Рольф, 1997.
22.
Шарыгин
И.Ф. Математика. Для поступающих в ВУЗы: Учебное пособие. – 4-е изд. –М.:
Дрофа, 2002.
23.
Шарыгин
И.Ф., Голубев В.И. Решение задач: Учебное пособие для 11 класса
общеобразовательных учреждений. – 2-е изд. – М.: Просвещение, 1995.
24.
Шахно
К.У. Сборник задач по элементарной математике повышенной трудности: Высшая школа,
1967.
25.
Якушева
Е.В., Попов А.В., Черкасов О.Ю., Якушев А.Г. Экзаменационные вопросы и ответы.
Алгебра и начало анализа 9 и 11 выпускные классы: Учебное пособие.- М.:
АСТ-Пресс, 2000.
|