Учебное пособие: Математична обробка результатів вимірів
Учебное пособие: Математична обробка результатів вимірів
МАТЕМАТИЧНА ОБРОБКА
РЕЗУЛЬТАТІВ ВИМІРІВ
1. Математична обробка
ряду рівноточних вимірів
Математична обробка ряду
рівноточних вимірів полягає в послідовному визначенні числових характеристик
вимірюваної величини.
Для зручності приведемо
послідовність обчислень при обробці ряду рівноточних вимірів. Припустимо, що в
результаті повторних рівноточних вимірів величини Х дотримано ряд результатів
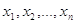 ( (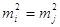 ) )
Обчислюють
1. Просту арифметичну
середину за формулою
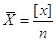
Для зручності обчислень
можна взяти умовне значення близьке до виміряних результатів х0. Обчислити різниці
 (i = l,n ) (i = l,n )
2. При відомому істинному
значенні X обчислюють величину систематичної похибки 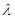 за формулою за формулою
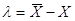
3. Абсолютні похибки
вимірів при заданому істинному значенні X
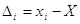 (i = l,n ) (i = l,n )
або ймовірні похибки, коли невідоме істинне
значення вимірюваної величини X
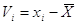
Контроль [Vi] = 0 — в межах точності обчислень.
4. Величини [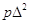 ] або [ ] або [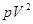 ] з контролем ] з контролем
Контроль
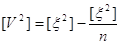
5. Середню квадратичну
похибку окремого виміру:
а) за формулою Гаусса
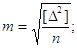
б) або за формулою
Бесселя
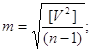
6. Середню квадратичну
похибку середнього арифметичного
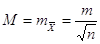
Далі обчислюють оцінки надійності і середніх квадратичних похибок m і М.
7. Середню квадратичну
похибку середньої квадратичної похибки
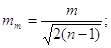
При цьому 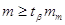 . Параметр t визначається за таблицями розподілу Стьюдента залежно від
заданої ймовірності . Параметр t визначається за таблицями розподілу Стьюдента залежно від
заданої ймовірності 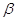 та числа ступенів вільності n. та числа ступенів вільності n.
8. Середню квадратичну
похибку середньої квадратичної похибки арифметичного середнього
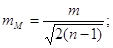
Надійність визначення СКП
арифметичного середнього М контролюють нерівністю
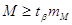
9. Визначають довірчі
інтервали для:
а) можливого значення
істинної величини
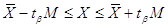
де 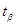 — параметр вибирається із таблиць
розподілу Стьюдента залежно від заданої ймовірності — параметр вибирається із таблиць
розподілу Стьюдента залежно від заданої ймовірності  та кількості ступенів вільності k = n - 1 та кількості ступенів вільності k = n - 1
б) можливих значень
результатів вимірів
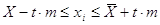 , ,
де параметр t вибирається так само, як і в
попередньому випадку.
Якщо в ряду вимірів є результати,
що виходять за межі визначеного параметра, то їх або повторюють, або виміри
виключають і попередні обчислення виконують повторно;
в) дисперсії та стандарти
середнього арифметичного
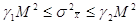
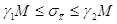
де m і М — середні квадратичні похибки,
обчислені за формулами.
Коефіцієнти 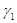 і і 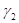 обчислюються за формулами обчислюються за формулами
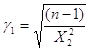 , , 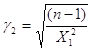
при використані формули
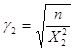 , , 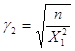
при використанні формули,
статистики 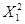 і і 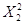 вибираються із таблиць
розподілу Пірсона за числом ступенів вільності (n-1) або n та
заданій імовірності вибираються із таблиць
розподілу Пірсона за числом ступенів вільності (n-1) або n та
заданій імовірності 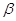 при при
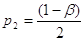 i i 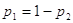
Середнє арифметичне
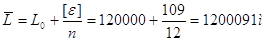
Середню квадратичну
похибку окремого виміру за формулою Бесселя
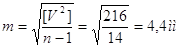
Середню квадратичну
похибку середнього арифметичного
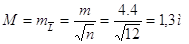
Середню квадратичну
похибку середньої квадратичної похибки
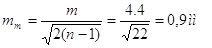
При 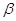 = 0,95 та n за таблицею = 0,95 та n за таблицею 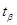 = 2,3 отримаємо = 2,3 отримаємо
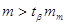
Середню квадратичну
похибку середньої квадратичної похибки арифметичного середнього

При 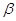 = 0,95 та = 0,95 та 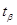 = 2,3 = 2,3
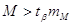 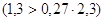 або (1,3 > 0,62) або (1,3 > 0,62)
Це говорить про те, що оцінки m та М отримані
надійно.
Обчислюють довірчі
інтервали:
а) для істинного значення
при 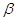 = 0,95 і = 0,95 і  = 2,3 = 2,3
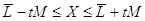 ; ;
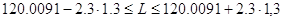
б) результатів вимірів
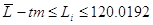
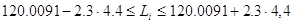
в) стандарти середнього
арифметичного при 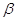 = 0,95 p2 = 0,03 і р1 = 0,97. k = n-1=11 Шляхом
лінійного інтерполювання визначаємо = 0,95 p2 = 0,03 і р1 = 0,97. k = n-1=11 Шляхом
лінійного інтерполювання визначаємо 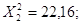 
Тоді 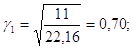 
Відповідно отримуємо
інтервал
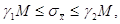 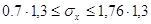 ( (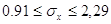 ) )
г) стандарти окремих
вимірів
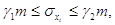 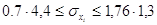 ( (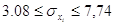 ) )
Можна обчислити і
відносні похибки
а) для істинного значення
довжини компаратора використаємо
інтервальну оцінку.
Похибка визначення складе
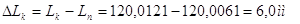
де 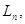 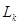 — початкове та кінцеве
значення інтервалу. — початкове та кінцеве
значення інтервалу.
Відносна гранична похибка
складе
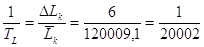 , ,
б) точність окремих
вимірів характеризується відносною граничною
похибкою
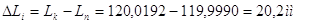
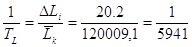
Залежно від заданих умов
приймають остаточне рішення про якість виконаних вимірів і можливості
використання компаратора.
2. Математична обробка
ряду нерівноточних вимірів
Приведемо послідовність
визначення числових характеристик багатократних повторних нерівноточних
вимірів. Якщо отримано статистичний ряд нерівноточних вимірів
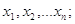 ( (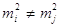 ) )
то обчислюють
1. Ваги вимірів за однією із можливих
формул
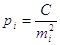 , , 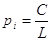 ; ;
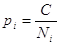 або або 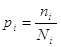
де 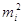 - емпіричні дисперсії
виміряних величин; - емпіричні дисперсії
виміряних величин;
Li — довжина лінії ходу, полігона і
т.д.;
Ni - кількість виміряних величин: кутів,
перевищень, ліній, штативів і т.д.;
ni - кількість вимірів (прийомів)
однієї шуканої величини.
2. Загальне середнє
арифметичне

Для зручності обчислень
можна взяти умовне значення близьке до отриманих результатів вимірів x0. Обчислити різниці
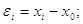 (i=l,n) (i=l,n)
Тоді
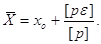
3. Абсолютні похибки
вимірів при заданому істинному значенні вимірюваної величини X
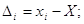 (i=l,n), (i=l,n),
або ймовірні похибки,
коли невідоме істинне значення
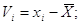
Контроль 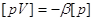 , де , де 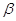 - похибка заокруглення
загального середнього арифметичного X. - похибка заокруглення
загального середнього арифметичного X.
4. Систематичну похибку  , при відомому істинному
значенні X або істинних похибках , при відомому істинному
значенні X або істинних похибках  за формулою за формулою
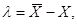 або або 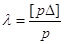
5. Величину [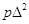 ] або ] або 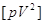 з контролем. з контролем.
Контроль: 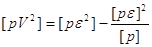
6. Середню квадратичну
похибку одиниці ваги за формулою
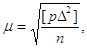 або або
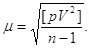
7. Середню квадратичну
похибку загального середнього арифметичного за формулою
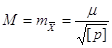
Виконують оцінку
надійності середніх квадратичних похибок 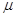 та
М. та
М.
8. Середню квадратичну
похибку середньої квадратичної похибки одиниці ваги
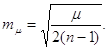
Надійність визначення
середньої квадратичної похибки одиниці ваги визначають нерівністю 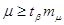 . Параметр . Параметр 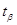 визначається за таблицею
розподілу Стьюдента за заданою ймовірністю визначається за таблицею
розподілу Стьюдента за заданою ймовірністю 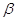 і
числом ступенів вільності k = n-1. і
числом ступенів вільності k = n-1.
9. Середню квадратичну
похибку середньої квадратичної похибки загального середнього арифметичного
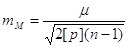
Надійність визначення СКП
загального середнього арифметичного М контролюють нерівністю
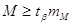 , ,
де 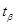 - параметр, що
визначається так само як і в попередньому випадку. - параметр, що
визначається так само як і в попередньому випадку.
10. Довірчі інтервали для
а) істинного значення
виміряної величини
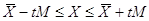
де t - параметр
вибирається з таблиць розподілу Стьюдента за ймовірністю 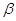 і кількістю ступенів
вільності k = n-1. і кількістю ступенів
вільності k = n-1.
б) стандарта загального
середнього арифметичного
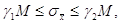
в) стандарта
одиниці ваги
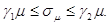
Коефіцієнти 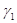 і і 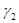 обчислюються так само як і
при рівноточних вимірах. обчислюються так само як і
при рівноточних вимірах.
При необхідності
обчислюють:
а) середні квадратичні
похибки окремих нерівноточних вимірів
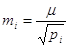
б) інтервальні оцінки для
окремих результатів ряду нерівноточних вимірів
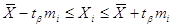
3. Оцінка точності функцій виміряних
величин
В практичній діяльності
для вимірювання шуканих величин часто застосовують посередні методи. При цьому
шукана величина Y визначається
шляхом обчислень по виміряних величинах Х1, Х2 ..., Хn. Шукану величину Y називають функцією, а виміряні
величини Хі - аргументами, тоді
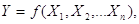
де Х1, Х2
..., Хn - істинні значення функції та її
аргументів.
Зрозуміло, що виміри виконуються з похибками, тому
і функція буде обтяжена похибкою. В результаті повторних вимірювань аргументів
Хi можна визначити їх точність, або їх
точність визначається методикою вимірювань на основі інструкцій і т.і.
Похибка функції буде
залежати від похибок її аргументів. Якщо виміряно аргументи Х1, Х2
..., Хn, то шляхом обчислень можна визначити
функцію
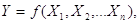
де Х1, Х2
..., Хn - виміряні величини з середніми
квадратичними похибками   ..., mxn. Припустимо, що нам відомі істинні
похибки вимірів ..., mxn. Припустимо, що нам відомі істинні
похибки вимірів  . Очевидно і функція отримає істинний приріст . Очевидно і функція отримає істинний приріст  . Функція зведеться до
вигляду . Функція зведеться до
вигляду
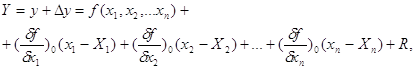
де 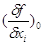 - часткові похідні від функції по
перемінних наближених значеннях аргументів; - часткові похідні від функції по
перемінних наближених значеннях аргументів;
xі —Хі = 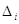 -
істинні похибки аргументів функції; -
істинні похибки аргументів функції;
R - величини другого та вищих порядків
малості і в подальших розрахунках може бути прийнятою за нуль, тобто R=0.
Визначимо приріст функції
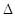 у, для чого від рівняння у, для чого від рівняння 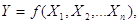 віднімемо рівняння віднімемо рівняння
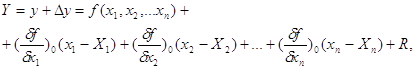
і отримаємо
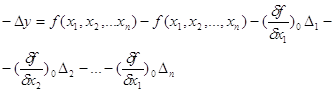
Для оцінки точності функцій застосуємо метод
повторних вимірювань аргументів. Тобто припустимо, що аргументи функції
виміряні n-разів і при відомих істинних похибках аргументів обчислено таку ж
кількість похибок функції, тобто
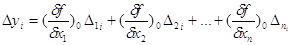 , (i = l,n) , (i = l,n)
Зведемо їх до квадрата,
складемо і поділимо на n.
Отримаємо
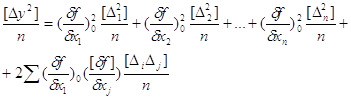
Із кореляційного аналізу
можна визначити коефіцієнт кореляції за формулою
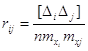
Тоді дисперсія функції
зведеться до вигляду
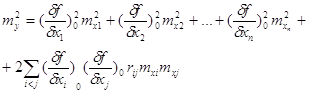
де 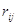 - коефіцієнт кореляції,
який виражає залежність між аргументами xi та xj. - коефіцієнт кореляції,
який виражає залежність між аргументами xi та xj.
Дві останні
формули виражають
дисперсію функції, тобто її точність залежно від виду функції і точності
залежних між собою аргументів.
Практично досить важко і
економічно невигідно визначати коефіцієнти кореляції. Тоді умовно приймають їх
незалежними, а коефіцієнт кореляції rij = 0.
Для незалежних аргументів
дисперсія функції буде
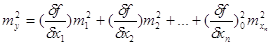
де my, m1,
m2, …, mn - середні
квадратичні похибки
функції та її аргументів.
В узагальненому вигляді
середню квадратичну похибку функції для незалежних аргументів виражають
формулою
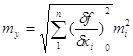
В теорії похибок вимірів
для визначення дисперсії функції застосовують правило:
1. Диференціюють функцію
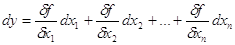
2. В отриманій формулі
зводять до квадрату кожен член разом із своїм знаком
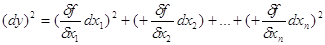
3. В формулі замінюють
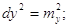 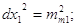 … … 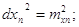
тобто
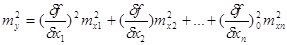
Визначення ваги
функції
Вага функції є
мірою відносної точності і її можна збільшувати або зменшувати в певну
кількість разів  . .
Розглянемо дисперсію
функції для незалежних аргументів.
Відомо, що 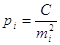 . Тоді можна замінити . Тоді можна замінити 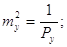  отримаємо: отримаємо:
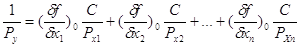
Це і є формула оберненої
ваги функції, після обчислення якої можна перейти до ваги функції. Коефіцієнт С
вибирають так, щоб значення ваги Ру було близьке до одиниці для зручності її
використання.
Для визначення ваги
функції в теорії похибок вимірів користуються правилом:
1. Визначають дисперсію
функції.
2. Дисперсії всіх
перемінних 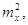 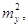 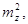 ..., і т. д. замінюють на обернені
ваги відповідно ..., і т. д. замінюють на обернені
ваги відповідно
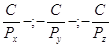 , …, і т. д. , …, і т. д.
Зазначимо, що вага однієї функції не
дає уявлення про точність функції. Її можна використати у порівнянні з вагами
функції однорідних фізичних величин. Вага функцій визначає відносно більшу або
меншу точність однієї функції порівняно з іншою.
Вага системи функції
Якщо маємо систему функцій
 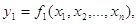
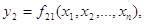
_ _ _ _ _ _ _ _ _
_ _
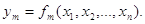
Вага системи функції для незалежних
аргументів визначається за формулою:
 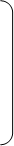 
a11 a12 … ain
a21
a22 … a2n
A = … … …
am1 am2
… amn
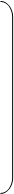  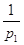
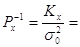 
…
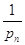
де 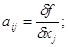 Кх –
кореляційна матриця аргументів хі; Кх –
кореляційна матриця аргументів хі; 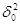 -
дисперсія одиниці ваги; -
дисперсія одиниці ваги; 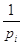 -
обернені ваги аргументів. -
обернені ваги аргументів.
Після
перемноження матриць отримаємо:
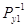 К12 К13...
К1m К12 К13...
К1m
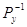 = K21 = K21 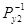 К23... К2m К23... К2m
… … … …
Km1 Km2
Km3 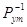
де 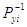 - обернені ваги функції уі; - обернені ваги функції уі;
Kij – кореляційні моменти, які
характеризують зв’язок між вагами функцій.
Коєфіцієнти
кореляції між функціями визначаються за формулою:
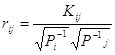
РОЗДІЛ 2. ВИПАДКОВІ ВЕЛИЧИНИ, ЇХ ХАРАКТЕРИСТИКИ І ЗАКОНИ
РОЗПОДІЛУ ЙМОВІРНОСТЕЙ
1. Випадкові величини
Випадкові події якісно
характеризують випадковий результат проведеного досліду. Разом з тим випадковий
результат можна характеризувати і кількісно.
Випадковою величиною
називають таку величину, яка в результаті досліду може набути будь-якого довільного
значення до того заздалегідь невідомо якого саме.
Поняття випадкової
величини є одним із важливих понять теорії ймовірностей. Позначимо випадкові
величини великими буквами латинського алфавіту - X, У, ..., а їх можливі
значення позначимо відповідними малими буквами х,у,... .
Випадкові величини в
практичній діяльності можуть бути дискретні та неперервні.
Дискретною (перервною)
випадковою величиною називають таку величину, яка може
приймати окремі кінцеві значення або їх нескінченну кількість (безліч, елементи
якої можуть бути занумеровані).
Приклади дискретних
випадкових величин:
1.
Кількість
правильних вимірів кута при 10 прийомах.
2.
Число бракованих
приладів в партії із n
штук.
Неперервною випадковою
величиною називають таку величину, можливі значення якої повністю заповняють
деякий інтервал (кінцевий або нескінченний) числової осі. Таким чином і число
можливих значень неперервної випадкової величини буде нескінченним.
Приклади неперервних
випадкових величин:
1. Помилка виміру довжини
лінії, чи величини кута.
2. Графік рівня води в
річці, отриманий за допомогою реєстраційного автоматичного
приладу.
Цілком зрозуміло, що при
випробуваннях окремі значення випадкових величин помітно відрізняються одне від
одного і на перший погляд вони не здаються неперервними. Але треба усвідомити,
що ці значення не можна перечислити заздалегідь і мова йде про ті значення, які
можна прийняти в результаті досліду. Появу того чи іншого значення не можна
заздалегідь задати точно, але можна шукати ймовірності того чи іншого значення
випадкової величини. Це означає, що випадкова величина володіє ймовірністю її
появи. Тому в практичній діяльності зручніше користуватися дискретними
випадковими величинами ніж неперервними випадковими величинами.
2. Закон розподілу
ймовірностей випадкових величин
В результаті досліду
неперервна випадкова величина X приймає одне із своїх можливих значень. Тобто
з'явиться одна подія із повної групи несумісних подій: X = х1, X = Х2,
..., X — хn. Кожне із
цих значень володіє ймовірністю появи, або
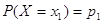 , , 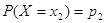 , ... , ... 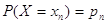
Так як всі можливі події утворюють повну групу несумісних подій, то сума ймовірностей всіх можливих значень
випадкової величини X дорівнює одиниці
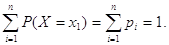
Цілком зрозуміло,
що випадкова величина буде повністю визначена, якщо вказати ймовірність кожної
із подій.
Законом розподілу
випадкової величини називають всяке співвідношення, що встановлює зв'язок між
можливими значеннями випадкової величини і відповідними ймовірностями.
Закон розподілу
дискретної випадкової величини задають:
1) аналітично;
2) чисельно у вигляді
таблиці;
3) графічно.
Аналітично закон
розподілу для дискретних випадкових величин задають за допомогою формул
розподілу ймовірностей при повторних випробуваннях. Ймовірність появи k-ої події при n - випробуваннях
розраховують за формулою.
Найбільш просто
закон розподілу дискретної випадкової величини X відображають у вигляді таблиці,
яку називають рядом розподілу випадкової величини.
Наочно ряд розподілу
відображають графічно. Для цього можливі значення випадкової величини Х1
відкладають по осі абсцис, а по осі ординат - відповідні їм імовірності Р.
Отримані вершини ординат з'єднують відрізками прямих ліній. Такий рисунок
називають багатокутником розподілу.
Слід пам'ятати, що
з'єднання вершин ординат проводиться тільки для більш наочного відображення.
При цьому, в відрізках поміж Х1 і Х2, Х2 і X3 і
далі, випадкова величина х немає значення і ймовірності її на цих відрізках
дорівнюють нулю. Другою властивістю багатокутника розподілу є те, що сума
ймовірностей всіх можливих значень випадкової величини (сума ординат) завжди
дорівнює одиниці. Це виходить з того, що всі можливі значення випадкової величини
X утворюють повну групу подій, сума ймовірностей яких дорівнює одиниці.
Немає сумніву, що ряд
розподілу чи багатокутник розподілу можна подати для дискретної випадкової
величини з кінцевим числом можливих значень. Однак ряд розподілу не можна побудувати
для неперервної випадкової величини, що має незчисленну безліч можливих
значень, які суцільно заповнюють деякий відрізок. Перелічити таку безліч
значень випадкової величини практично неможливо. Проте, треба мати таку характеристику розподілу ймовірностей, яка б
відображала як дискретні, так і неперервні випадкові величини. Нею є функція
розподілу.
Функцією розподілу або
інтегральним законом розподілу випадкової величини X називається задання
ймовірності події виконання нерівності X < х, де х - деяка поточна змінна,
її розглядають як функцію аргументу х і визначають за формулою
F(x) =
P(X<x)
Функцію розподілу F(х) називають інтегральною функцією розподілу або інтегральним законом розподілу. Вона
має досить просту геометричну інтерпретацію. Розглянемо випадкову величину, як
випадкову точку X осі ОХ, що в результаті випробування може прийняти те чи інше
положення. Тоді функція розподілу F(х) є ймовірністю того, що випадкова точка X в результаті випробування
попаде зліва від точки х.
Функція дискретної випадкової
величини X, що може приймати значення Х1,Х2, ... , xn буде мати вигляд
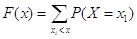
При цьому додавання ймовірностей розповсюджується на всі можливі значення випадкової-величини, які за своєю величиною менші аргументу х. Це означає, що функція розподілу дискретної випадкової величини X розривна і зростає стрибками при переході через точки можливих її значень Х1, Х2, ... , хn.
Оскільки функція
розподілу дискретної випадкової величини виглядає як сходинкова ламана
лінія, тому її називають сходинковим графіком.
Якщо випадкова величина
неперервна, то вона має ймовірність в кожній точці осі х. Згідно з формулою
функція розподілу буде зростати поступово, тому що можливі значення випадкової
величини неперервно заповнюють будь-який інтервал на осі х. Тоді графік
виглядатиме як монотонне зростаюча функція розподілу F(х) на інтервалі від а до b.
Функція розподілу має
властивості:
1. Функція розподілу F(х)
є зростаючою і міститься між нулем та одиницею 0 < F(х) < 1.
Це випливає з того, що
функція F(х) визначається як імовірність випадкової події X < х.
2. Ймовірність виникнення
випадкової величини в інтервалі від  до до 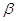 дорівнює різниці значень
функції на кінцях інтервалу дорівнює різниці значень
функції на кінцях інтервалу
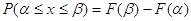
Визначимо подію А того,
що випадкова величина х < 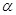 та
подію В для випадку х < та
подію В для випадку х < 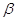 . .
Подія С відображає те, що
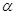 < х < < х < 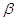 . В цьому випадку подія В
буде складатися із суми двох несумісних подій А і С, тобто В = А + С. Згідно з
теоремою додавання ймовірностей маємо . В цьому випадку подія В
буде складатися із суми двох несумісних подій А і С, тобто В = А + С. Згідно з
теоремою додавання ймовірностей маємо
P (B) = P(A) +
P(C)
Якщо функція в точці 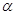 неперервна, то граничне
значення дорівнює нулю. При розриві функції в точці (X її граничне значення
буде дорівнювати значенню стрибка функції F (х). неперервна, то граничне
значення дорівнює нулю. При розриві функції в точці (X її граничне значення
буде дорівнювати значенню стрибка функції F (х).
З цього робимо висновок,
що ймовірність випадкової величини в точці для неперервної функції дорівнює
нулю. Це явище називають парадоксом теорії ймовірностей.
Проте нульова ймовірність
події лише зазначає, що частота цієї події невпинно спадає при збільшенні числа
дослідів, однак це не означає, що ця подія неможлива.
3. Функція розподілу
випадкової величини є зростаючою функцією, тобто при 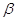 > > 
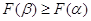
Маємо 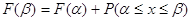
Так як імовірність
будь-якої події є додатне число, то 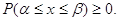
3. На мінус
нескінченності функція розподілу дорівнює нулю, а на плюс нескінченності -
одиниці, тобто  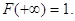
Це цілком вірно, так як
при необмеженому переміщенні точки х вліво, попадання випадкової точки X лівіше
х максимально стає неможливою подією і 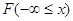 =
0. В той же час при необмеженому переміщенні точки х вправо попадання
випадкової точки X зліва від х практично стає достовірною подією, тоді =
0. В той же час при необмеженому переміщенні точки х вправо попадання
випадкової точки X зліва від х практично стає достовірною подією, тоді 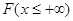 = 1. = 1.
За допомогою функції
розподілу можна знайти ймовірність випадкової величини в будь-якому інтервалі
або в кожній точці можливих значень для дискретної випадкової величини. Тому
функція розподілу однозначно визначає закон розподілу випадкової величини.
Більш наочно характер
розподілу неперервної випадкової величини в невеликих інтервалах числової осі х
дає функція щільності розподілу ймовірностей або диференціальний закон
розподілу.
Якщо маємо функцію
розподілу F(х) випадкової величини X, то
ймовірність попадання її на елементарну ділянку (х, х + 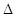 х) згідно з попередньою формулою буде: х) згідно з попередньою формулою буде:
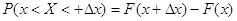
Знайдемо середню
ймовірність, що припадає на одиницю довжини ділянки 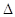 х х
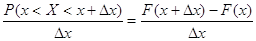
Функцією щільності
розподілу випадкової величини в точці х є
граничне відношення ймовірності попадання її на елементарну ділянку від х до х +
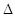 х до довжини цієї ділянки х до довжини цієї ділянки 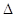 х, коли х, коли 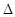 х наближається до нуля. х наближається до нуля.
Її позначають 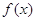 або (х). Зміст функції
щільності розподілу або (х). Зміст функції
щільності розподілу 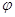 (х) полягає в
тому, що вона вказує, як часто з'являється випадкова величина X навколо точки х
при повторенні дослідів. (х) полягає в
тому, що вона вказує, як часто з'являється випадкова величина X навколо точки х
при повторенні дослідів.
Функція щільності
розподілу має властивості:
1. Щільність розподілу
невід'ємна, тобто 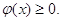
2. Функція розподілу
випадкової величини дорівнює інтегралу від функції щільності в інтервалі від - 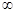 до х до х 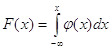
3. Ймовірність попадання
неперервної випадкової величини X на відрізку (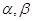 )
дорівнює інтегралу від функції щільності розподілу, взятому за кінцевими
значеннями цього відрізка )
дорівнює інтегралу від функції щільності розподілу, взятому за кінцевими
значеннями цього відрізка
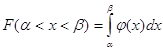
Геометричний зміст цього
результату полягає в тому, що ймовірність появи випадкової величини в інтервалі
від 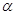 до до 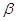 дорівнює площі
криволінійної трапеції. дорівнює площі
криволінійної трапеції.
4. Інтеграл в
нескінченних межах від - 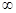 до + до + 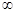 дорівнює одиниці дорівнює одиниці
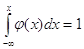
Ймовірність попадання
випадкової величини X на елементарний інтервал dx з точністю до нескінченно малих вищого порядку чим 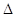 х дорівнює х дорівнює  (х) dх, (так як (х) dх, (так як 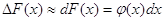 ). Геометричний зміст цього
виявляється в тому, що це є площа елементарного прямокутника з висотою ). Геометричний зміст цього
виявляється в тому, що це є площа елементарного прямокутника з висотою 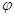 (х) і основою dх. Величина (х) і основою dх. Величина 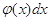 називається елементом
імовірності. називається елементом
імовірності.
3. Числові
характеристики випадкових величин
Закон розподілу повністю характеризує випадкову величину з точки зору ймовірності її появи в будь-якому інтервалі числової осі 0х. Разом з тим при вирішенні великої кількості практичних задач
достатньо знати тільки деякі характерні риси закону розподілу. В теорії
ймовірностей їх називають числовими характеристиками випадкової величини X.
Вони в досить стислому вигляді характеризують той чи інший закон розподілу.
Властивості випадкової
величини X характеризують параметри: математичне сподівання, мода, медіана,
дисперсія, середнє квадратичне відхилення та стандарт. Більш узагальненими
основними характеристиками випадкових величин є моменти випадкової величини.
1) Математичне сподівання
Якщо дискретна випадкова
величина X володіє можливими значеннями х1, Х2,..., хn
з імовірностями p1,p2, pn то
математичне сподівання випадкової величини X визначається за формулою
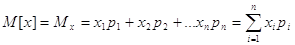
де 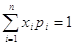 , так як поява однієї із можливих
подій є достовірна подія. , так як поява однієї із можливих
подій є достовірна подія.
Якщо випадкова величина X
має нескінченне число можливих значень, то
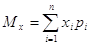
Математичним сподіванням випадкової величини X
називається сума добутку всіх можливих значень випадкової величини на
ймовірності цих значень.
Математичним сподіванням
неперервної випадкової величини X, можливі значення якої належать відрізку [а,
в], називають визначений інтеграл 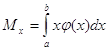
а де 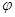 (х) - щільність імовірності
розподілу випадкової величини. (х) - щільність імовірності
розподілу випадкової величини.
Математичне сподівання
має ту ж розмірність, що і випадкова величина, та має властивості:
1. Математичне сподівання
постійної величини дорівнює величині постійної, тобто М(С) = С.
2. Постійний множник
можна виносити за знак математичного сподівання М(СХ) = СМХ.
3. Математичне сподівання
суми декількох випадкових величин дорівнює сумі їх математичних сподівань M (x+y+…+k) = Mx + My + … + Mk
4. Математичне сподівання
добутку декількох взаємно незалежних випадкових величин дорівнює добутку їх
математичних сподівань

Математичне сподівання
може бути як додатнім, так і від'ємним.
Відомо, що для повної
групи подій 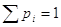 . .
Таким чином, виявляється
механічна інтерпретація математичного сподівання. Воно буде абсцисою центру
тяжіння системи матеріальних точок.
Якщо ймовірності появи
випадкових величин xі тобто
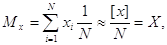
де X - середнє
арифметичне значення випадкової величини.
Це означає, що
математичне сподівання приблизно дорівнює середньому арифметичному значенню
випадкової величини. Воно буде тим точніше, чим більше буде проведено дослідів.
2) Мода і медіана
випадкової величини
Модою Мо дискретної
випадкової величини називають таке її значення, що має найбільшу ймовірність.
Практично, якщо маємо
дискретний ряд розподілу, то знаходимо таке k-е значення випадкової величини х, що має найбільшу величину ймовірності Pn(k).
Для неперервної
випадкової величини модою буде таке її значення, що має максимум щільності
розподілу, тобто 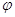 (Мо) = mах. (Мо) = mах.
Якщо многокутник
розподілу або крива розподілу має два або більше максимумів, то такий розподіл
називають двохмодальним чи багатомодальним.
Медіаною Ме випадкової
величини X називають таке її значення, відносно якого ймовірність появи як
більшого, так і меншого значення випадкової величини X має приблизно однакову
ймовірність, тобто
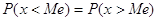
Геометрична медіана - це
абсциса точки, де площа кривої розподілу розділяється наполовину. Тоді функція
розподілу в точці Ме дорівнює математичне сподівання, мода і медіана
збігаються, тобто
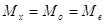
3) Дисперсія і середнє
квадратичне відхилення
Очевидно, що величину
розсіювання для кожної випадкової величини від математичного сподівання можна
обчислити, тобто 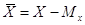
Величину 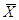 називають центрованою випадковою
величиною. Так як імовірність появи центрованих випадкових величин X справа і
зліва від Мх однакова, то її математичне сподівання дорівнює нулю і не може
характеризувати розсіювання її значень. Тому якістю міри розсіювання X беруть
математичне сподівання від квадрата відхилення випадкової величини від її
математичного сподівання і називають його дисперсією. називають центрованою випадковою
величиною. Так як імовірність появи центрованих випадкових величин X справа і
зліва від Мх однакова, то її математичне сподівання дорівнює нулю і не може
характеризувати розсіювання її значень. Тому якістю міри розсіювання X беруть
математичне сподівання від квадрата відхилення випадкової величини від її
математичного сподівання і називають його дисперсією.
Дисперсією випадкової величини є математичне
сподівання квадрата відхилення випадкової величини від її математичного
сподівання, тобто
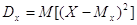
Для дискретної випадкової
величини дисперсія матиме вигляд суми
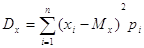
для неперервної це буде
інтеграл

Дисперсія має розмірність
квадрата розмірності випадкової величини, що не зовсім зручно. Тому для
характеристики міри розсіювання випадкової величини приймають додатковий
квадратичний корінь із дисперсії. Цю характеристику називають середнім
квадратичним відхиленням або стандартам і позначають символом 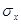
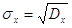
Стандарт має таку саму розмірність, як і випадкова
величина X. Дисперсія має такі властивості:
1. Дисперсія постійної
величини дорівнює нулю D (C) = 0.
2. Дисперсія добутку
постійної величини на випадкову величину дорівнює добутку квадрата постійної
величини на дисперсію випадкової величини D(CX) = C2Dx
Якщо маємо декілька таких
добутків, то 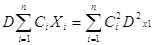
3. Дисперсія випадкової
величини дорівнює математичному сподіванню її квадрата мінус квадрат її
математичного сподівання
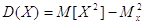
4). Моменти випадкової
величини
Узагальненням основних
числових характеристик випадкових величин є моменти випадкової величини.
Визначають початкові та центральні моменти.
Початковим моментом k-го
порядку випадкової величини Xk називають математичне сподівання від величини X , тобто
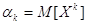
Для дискретної випадкової
величини початковий момент буде
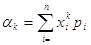
для неперервної 
При порівняні формул
видно, що початковий момент першого порядку є математичне сподівання випадкової
величини, тобто 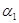 = Мх. = Мх.
Центральним моментом k-го порядку випадкової величини X
називають математичне сподівання від величини (X-Mx)k
Очевидно, що центральний момент першого порядку
завжди буде дорівнювати нулю.
5) Асиметрія та ексцес.
Третій центральний момент
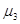 служить характеристикою
асиметрії (скошеність) розподілу. Якщо служить характеристикою
асиметрії (скошеність) розподілу. Якщо 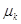 =
0, то ми маємо симетричний розподіл випадкової величини відносно математичного
сподівання. =
0, то ми маємо симетричний розподіл випадкової величини відносно математичного
сподівання.
Асиметрія — це відношення
третього центрального моменту до середнього квадратичного відхилення в третьому
степені
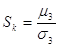
Математичне сподівання,
мода, медіана, дисперсія, середнє квадратичне відхилення, моменти, асиметрія і
ексцес використовують для характеристики випадкових величин при вирішенні
великої кількості практичних задач, коли закон розподілу або не потрібний, або
його не можна визначити. Треба пам'ятати, що кожна із числових характеристик
відображає ту чи іншу властивість закону розподілу.
Центральні моменти можна
виразити через початкові моменти
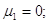
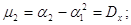
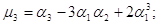
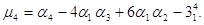
4. Нормальний закон
розподілу випадкових величин
Нормальний закон розподілу
випадкових величин має важливе значення в теорії ймовірностей і найчастіше
зустрічається на практиці. Головна його властивість полягає в тому, що серед
інших законів він є граничним законом, до якого наближуються інші закони
розподілу в досить частих подібних типових умовах. Доведено, що більшість
випадкових величин, якому б закону розподілу не підкорялися, в сумі великого
числа додатних нівелюються, а сума їх підкоряється закону досить близькому до
нормального закону. Це твердження відноситься і до результатів геодезичних
вимірів.
Неперервна випадкова
величина має нормальний розподіл, якщо
щільність імовірності має рівняння
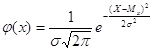
де е = 2,718..., 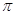 = 3,141..., Мх
- математичне сподівання, = 3,141..., Мх
- математичне сподівання, 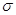 — середнє квадратичне відхилення (стандарт). Мх та — середнє квадратичне відхилення (стандарт). Мх та
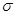 називають параметрами
нормального закону розподілу. Якщо відомі значення Мх і називають параметрами
нормального закону розподілу. Якщо відомі значення Мх і 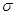 , то щільність імовірності
повністю визначена. , то щільність імовірності
повністю визначена.
Відмітимо деякі
властивості кривої нормального розподілу:
1. Крива розподілу
симетрична відносно ординати, яка проходить через точку Мх.
2. Крива має один
максимум при х = Мх і дорівнює 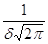
3. При 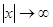 гілки кривої асимптотично
наближаються до осі Ох гілки кривої асимптотично
наближаються до осі Ох
4. Якщо 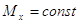 , то зміна значення
математичного сподівання Мх призводить
до зміщення кривої розподілу вздовж осі Ох. , то зміна значення
математичного сподівання Мх призводить
до зміщення кривої розподілу вздовж осі Ох.
5. При 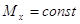 і зміні величини
середнього квадратичного
відхилення крива
розподілу стає більш гостроверхою або плосковерхою. і зміні величини
середнього квадратичного
відхилення крива
розподілу стає більш гостроверхою або плосковерхою.
При вирішенні практичних
задач, нормальний розподіл відіграє важливу роль. Якщо випадкова величина X
підкоряється нормальному закону розподілу, то ймовірність її попадання на
ділянку (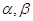 ) дорівнює ) дорівнює
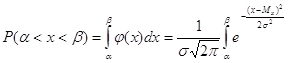
Згідно з четвертою та
п'ятою властивостями для різних випадкових величин X буде своя крива розподілу.
Щоб уникнути цього визначають нормований нормальний закон розподілу. Вводять
нормовану випадкову величину t
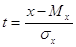 , ,
для якої математичне
сподівання  , а квадратичне відхилення , а квадратичне відхилення 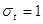 . .
Інтеграл не можна
виразити через елементарні функції. Тому його обчислюють через спеціальну
функцію, що є визначеним інтегралом від величини 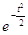 (інтеграл імовірностей. (інтеграл імовірностей.
Іноді приводять
таблицю функції 2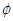 (t) для обчислення ймовірності
попадання нормально розподіленої випадкової величини X в симетричні інтервали від -t до t. (t) для обчислення ймовірності
попадання нормально розподіленої випадкової величини X в симетричні інтервали від -t до t.
Функцію 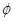 (t) називають нормованою функцією Лапласа або інтегралом
імовірностей. (t) називають нормованою функцією Лапласа або інтегралом
імовірностей.
РОЗДІЛ
3. СИСТЕМИ ВИПАДКОВИХ ВЕЛИЧИН. ГРАНИЧНІ ТЕОРЕМИ ТЕОРІЇ ЙМОВІРНОСТЕЙ
1. Поняття та закон
розподілу системи випадкових величин
До цього часу ми розглядали одномірну випадкову величину X. Однак в сучасній теорії
математичної обробки
результатів багаторазових повторних геодезичних вимірювань використовують багатомірні випадкові величини. Багатомірна випадкова величина може
складатися із декількох компонентів і бути двомірною, тримірною і так далі.
Так, наприклад, координати точки на площині визначаються двома випадковими
величинами: абсцисою X та ординатою У; положення точки в просторі визначається
вже трьома координатами - X, Y та
висотою Н.
Сумісна дія двох чи
більше випадкових величин приводить до системи випадкових величин. Умовимось
систему декількох випадкових величин X, У, ..., N позначати (X, У, ..., N). При вивченні системи випадкових
величин визначають характеристики як кожної випадкової величини, так і зв'язки
та залежність між ними. А це вже більш складні задачі.
Домовимось, що систему
двох випадкових величин (Х, У) ми будемо розглядати як випадкову точку на
площині х0у з координатами X і У, або як випадковий вектор на площині з
випадковими складовими X i У. Систему трьох випадкових величин (X, У, Z) - як випадкову точку в тримірному
просторі або, як випадковий вектор в просторі. За аналогією, систему n -випадкових величин (X, У, ..., N) розглядають як випадкову точку в n-мірному просторі або, як n-мірний випадковий вектор.
Законом розподілу системи
випадкових величин називають співвідношення, що встановлює зв'язок між
областями можливих значень системи випадкових величин і ймовірностями появи їх
в цих областях.
Закон розподілу системи
випадкових величин можна задавати в різних формах. Покажемо табличний спосіб
розподілу системи дискретних випадкових величин.
Якщо X та У - дискретні
випадкові величини, значення яких дорівнюють (ХbУj), де і
= 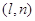 , а j = ( , а j = (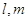 ),
то їх розподіл системи можна характеризувати ймовірностями рij = Р(Х = х1; Y = y1. Це означає, що коли випадкова величина X приймає значення х1
одночасно і величина Y прийме значення уj ),
то їх розподіл системи можна характеризувати ймовірностями рij = Р(Х = х1; Y = y1. Це означає, що коли випадкова величина X приймає значення х1
одночасно і величина Y прийме значення уj
Всі можливі події (X = xі,
Y = yj) і = 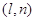 ,
а j = ( ,
а j = ( )
складають повну групу несумісних подій і тому )
складають повну групу несумісних подій і тому

2. Система двох
випадкових величин
В практиці геодезичних
вимірів досить часто взаємодіють дві випадкові величини X та У, тобто двомірні
випадкові величини. В попередньому параграфі ми наводили приклад з координатами
точки. При лінійних вимірах взаємодіють - довжина мірного приладу та
температура. При дослідженнях деформацій інженерних споруд взаємодіють —
величина осідання та інтервал часу і так далі.
Закон розподілу системи
двох випадкових величин задають функцією розподілу та щільністю розподілу.
Функцією розподілу
системи двох випадкових величин називають функцію двох аргументів F (х,у), що
дорівнює ймовірності сумісного виконання двох нерівностей Х<х і У < у,
тобто
F(x,y) = P
(X<x I Y<y)
Геометричне функцією
розподілу системи двох випадкових величин є ймовірність попадання випадкової
точки (Х,У) в нескінченний квадрат площини з вершиною в точці (х,у).
Функція розподілу має
такі властивості:
1. Якщо один із
аргументів наближається до плюс нескінченності, то функція розподілу системи
наближається до функції розподілу випадкової величини другого аргументу, тобто
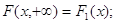
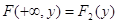
2. При наближенні обох
аргументів до плюс нескінченності функція розподілу F (х,у) наближається до
одиниці:
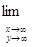 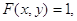 або або 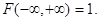
3. При наближенні одного чи обох аргументів до мінус
нескінченності функція розподілу наближається до нуля:
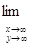 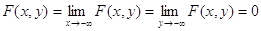
Практичне значення мають
системи неперервних випадкових величин, розподіл яких характеризують щільністю
розподілу 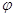 (х, у). За допомогою неї
більш просто знаходять імовірність попадання в різні області, а опис розподілу
системи випадкових величин стає більш наочним. (х, у). За допомогою неї
більш просто знаходять імовірність попадання в різні області, а опис розподілу
системи випадкових величин стає більш наочним.
Щільність розподілу
системи двох випадкових неперервних величин визначають як другу змішану
часткову похідну від функції F(х,у),
тобто
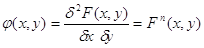
Функція розподілу F(х,у)
визначається за формулою
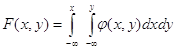
Щільність розподілу
системи двох випадкових величин має властивості:
1. Щільністю розподілу є
функція 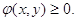
2. Подвійний інтеграл з нескінченними межами від функції щільності розподілу дорівнює одиниці:
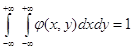
Геометрично це свідчить про те, що об'єм тіла,
відмежованого поверхнею розподілу і площиною х0у, дорівнює одиниці.
Щільності розподілу
величин х та у, що входять в систему, визначають за формулами:
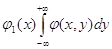
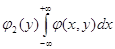
Тобто, для визначення
щільності розподілу однієї із системи випадкових величин, треба проінтегрувати
в необмежених межах щільність розподілу системи 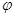 (х,у)
за аргументом другої випадкової величини. (х,у)
за аргументом другої випадкової величини.
Якщо відомі щільності
розподілу окремих випадкових величин системи і випадкові величини х та у
незалежні між собою, то можна визначити закон їх сумісного розподілу за
формулою

Поняття залежності та
незалежності випадкових величин має велике значення в теорії ймовірностей та
при математичній обробці результатів вимірів.
Випадкова величина X буде
незалежною від випадкової величини У, якщо закон розподілу величини X не
залежить від прийнятого значення величини У, тобто

і навпаки, для
випадкової величини Y маємо
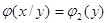
Якщо вони взаємно залежні
між собою, то 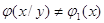 ; ; 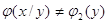
Випадкові величини Х і У
незалежні, якщо щільність сумісного розподілу 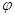 (х,у)
можна визначити у вигляді добутку двох множників, кожен із яких утримує тільки
величини х та у, тобто (х,у)
можна визначити у вигляді добутку двох множників, кожен із яких утримує тільки
величини х та у, тобто 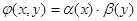
Додамо, що при
розкладанні, функції 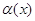 , , 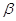 (у) з точністю до постійної множників
збігаються з щільностями розподілу (у) з точністю до постійної множників
збігаються з щільностями розподілу 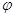 1(х) і 1(х) і  2(у). 2(у).
Між випадковими
величинами виникає функціональна або стохастнчна (ймовірна) залежність.
Функціональною залежністю між
випадковими величинами X і У називають таку
залежність, коли кожному значенню X відповідає точне значення У.
Стохастичною (ймовірною) залежністю між випадковими величинами X і У називають таку залежність, при
якій кожному значенню х можна вказати розподіл величини у, яке змінюється при
зміні х.
Така залежність в практичній діяльності
зустрічається досить часто. Наприклад, зріст та вага людини, висота і товщина
дерева в лісі, величина деформації інженерних споруд, час їх експлуатації і
т.д.
Тобто у випадку ймовірної
залежності на кожне точне значення аргументу х можна вказати значення
випадкової величини у з певною мірою ймовірності (Ру).
Система двох випадкових
величин може підкорятися різним законам розподілу. Проте в практиці геодезичних
вимірювань найбільше розповсюдження має нормальний закон розподілу.
3.
Числові характеристики системи двох випадкових величин. Кореляційний момент,
коефіцієнт кореляції і рівняння
регресії
Найбільш повними
ймовірними характеристиками системи двох випадкових величин є закон розподілу.
Однак в практичній діяльності не завжди є можливість визначити його. Тому при
дослідженнях систему двох випадкових величин характеризують їх числовими
характеристиками: початковими та центральними моментами.
Початковим моментом 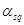 порядку s, q системи (X, У) називається математичне сподівання від
добутка Xs на Y9. порядку s, q системи (X, У) називається математичне сподівання від
добутка Xs на Y9.
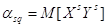
Для системи дискретних
випадкових величин

Між випадковими величинами X і У може
виникати зв'язок. Кореляційний момент Х і Y характеризує силу або щільність
зв'язку. Відомо, якщо між випадковими величинами існує ймовірний зв'язок
(залежність), то зі зміною випадкової величини X змінюється закон розподілу
випадкової величини У. В той же час закон розподілу задають кривою розподілу у
=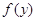 . Характер кривих може бути
різним, тому і відрізняють декілька типів імовірної залежності. Одним із
найбільш розповсюджених типів є кореляційна залежність, за якої заміна
аргументу х призводить до зміни математичного сподівання величини у. В першому
випадку ми маємо прямолінійну кореляцію. При дослідженнях можуть виникнути й
інші типи кореляційної залежності. . Характер кривих може бути
різним, тому і відрізняють декілька типів імовірної залежності. Одним із
найбільш розповсюджених типів є кореляційна залежність, за якої заміна
аргументу х призводить до зміни математичного сподівання величини у. В першому
випадку ми маємо прямолінійну кореляцію. При дослідженнях можуть виникнути й
інші типи кореляційної залежності.
Кореляційну залежність
часто називають кореляцією. Кореляційний
момент має розмірність, яка залежить від розмірності випадкових величин X і У. Тому
для оцінки сили зв'язку між випадковими величинами системи (X, У)
використовують не коефіцієнт зв'язку Кху, а безрозмірне відношення
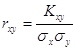 , ,
яке називають коефіцієнтом
кореляції випадкових величин Х і У. Коефіцієнт кореляції змінюється в межах від
-1 до +1, тобто 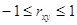
Якщо r > 0, то маємо позитивну
кореляцію, тобто із збільшенням абсциси х, збільшується величина ординати у і
навпаки при r < 0 .
Якщо випадкові величини X і Y незалежні, то кореляційний момент і коефіцієнт кореляції дорівнює нулю,
тобто Кху = 0 і rxy = 0.
Дві корельовані випадкові
величини завжди є взаємозалежними, але дві залежні величини не завжди є
корельованими. Прикладом цього може бути система випадкових величин (X, Y)
рівномірно розподілена в межах кола з центром на початку координат. Розрахунки
показують, що величини X і У залежні, а кореляційний момент Кxу = 0, а це означає, що і rxy = 0.
Випадкові величини X і У
називають корельованими, якщо 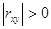 i при i при 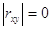 - некорельованими. - некорельованими.
ГЛАВА II. ЕЛЕМЕНТИ
МАТЕМАТИЧНОЇ СТАТИСТИКИ.
СТАТИСТИЧНА ОЦІНКА ПАРАМЕТРІВ РОЗПОДІЛУ
1. Основні поняття і задачі математичної статистики.
Генеральна сукупність та вибірка
Математична статистика - дисципліна, яка займається
регістрацією, збором, описом і аналізом експериментальних даних з метою
вивчення закономірностей масових випадкових явищ.
Таким чином, всі задачі
математичної статистики зводяться до визначення методів обробки результатів
експериментальних досліджень (спостережень) масових випадкових явищ.
Найбільш типовими
задачами математичної статистики є:
1. Оцінка невідомої
функції розподілу за результатами вимірів. Якщо за результатами досліджень
випадкової величини X одержано значення x1, x2, … xn то необхідно приблизно оцінити
невідому функцію розподілу Р(х).
2. Оцінка точності
невідомих параметрів розподілу. При вирішенні цього питання обчислюють
параметри функції розподілу випадкової величини на основі отриманих результатів
експерименту і оцінюють їх значення.
3. Статистична перевірка
гіпотез. Якщо за результатами експерименту визначено функцію розподілу Р(х)
випадкової величини X, то вирішується питання: чи дійсно випадкова величина X
має розподіл Р(х) ?
При дослідженнях випадкових
явищ виконують досить велику кількість випробувань (експериментів) - N.
Генеральна сукупність -
це сукупність значень результатів досліджень (вимірів). Досить часто мають на
увазі, що число N може бути нескінченним.
Проте практично виконати
нескінченну кількість дослідів (вимірів) або обстежити нескінченну кількість
виробів неможливо, і економічно невигідно. В цьому випадку із всієї генеральної
сукупності відбирають обмежене число результатів експерименту.
Вибірковою сукупністю або
просто вибіркою називають сукупність випадково вибраних результатів чи
об'єктів.
Проте вибірка може як
досить точно характеризувати досліджуване випадкове явище, так і ні.
Представницькою або
презентабельною вибірковою називають об'єм вибірки n із генеральної сукупності N,
який дозволяє повною мірою визначити характеристики генеральної сукупності.
Інформація буде більш імовірною, коли результати досліджень, що складають
вибірку, будуть незалежними.
2. Розподіл статистичних рядів
Практично, до початку
досліджень випадкового явища, заздалегідь невідомо, якому закону розподілу
будуть підпорядковуватися результати експерименту. Для його визначення над
випадковою величиною X виконують низку незалежних експериментів (вимірів).
Статистична таблиця є
початковою формою запису статистичного матеріалу, який може оброблятися різними
методами.
Однак при великій
кількості експериментів (вимірів) їх результати практично неможливо показати в
статистичній таблиці. Тоді результати спостережень розділяють на групи. Кожна
група містить деяку кількість (частоту) результатів, що належать визначеному
інтервалу. Довжина інтервалу розраховується за формулою Г.А.Стерджеса
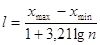
де n - кількість результатів
спостережень.
Можна задати число
інтервалів k. Тоді довжину інтервалу визначають за формулою
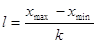
Значення інтервалу l заокруглюють до зручного цілого
значення так, щоб число їх було в межах  . .
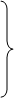 Потім визначають граничні значення інтервалів за
формулами Потім визначають граничні значення інтервалів за
формулами
для 1-ої групи 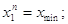 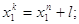
для 2-ої групи 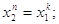 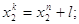
для k-ої групи 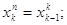 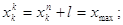
де  , , 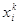 - відповідно початкове та
кінцеве значення абсциси х (результатів вимірів). - відповідно початкове та
кінцеве значення абсциси х (результатів вимірів).
Для кожної групи
підраховують частоту результатів Vi, які попадають в граничні значення 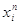 і і 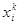 , і статистичну ймовірність , і статистичну ймовірність
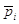 за формулою за формулою
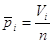 , ,
причому V1 + V2
+ ...+ Уk = n; р1 + р2+...
+ рk = 1.
За допомогою статистичної
таблиці або статистичної сукупності можна побудувати статистичну функцію
розподілу випадкової величини X.
3. Оцінювання
параметрів закону розподілу
Відомо, що
випадкова величина X характеризується законом
розподілу, що має деякі невідомі параметри a(a1, a2, …, аk). Якщо в результаті виконаного експерименту нами
отримано статистичний ряд Х1, Х2, ..., Х3 то
очевидно можна знайти надійну оцінку параметра а.
Припустимо, що на основі
обробки статистичного ряду отримано параметра, який буде оцінкою невідомого
параметра 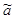 . Разом з тим, він буде
функцією від випадкових величин Х1, Х2, ..., Х3
тобто . Разом з тим, він буде
функцією від випадкових величин Х1, Х2, ..., Х3
тобто
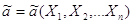
Таким чином і обчислений
параметр а буде випадковою величиною, закон розподілу якого залежить від закону
розподілу випадкової величини X і від числа експериментів n. При цьому оцінка а буде мати
практичну цінність, якщо володіє властивостями:
1 . Незміщеності. При
цьому повинна виконуватися умова
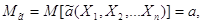
де а - істинне значення
параметра.
2. Обгрунтованості. Тобто
за ймовірністю вона зводиться до оцінюваного параметра при нескінченному
збільшенні кількості дослідів, тобто
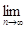 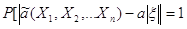
де 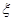 - як завгодно мале
позитивне число. - як завгодно мале
позитивне число.
3. Ефективності. Це
означає, що дисперсія оцінки а повинна бути мінімальною, тобто
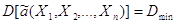
При цьому буде мінімальна
ймовірність появи грубої помилки при визначенні наближеного значення невідомого
параметра.
Таким чином при розробці
методів обробки статистичних даних для визначення оцінок наближених значень
невідомих параметрів треба виходити з їх властивостей. Оцінки параметрів закону
розподілу, що відповідають всім трьом властивостям називають доброякісними.
Практично розроблено три
способи визначення оцінок: метод моментів; метод максимальної правдоподібності
(ММП); метод найменших квадратів (МНК).
В методі моментів
значення теоретичних моментів заміняють значеннями емпіричних моментів, які
обчислюють за результатами статистичних рядів чи статистичної сукупності.
В методі максимальної
правдоподібності (ММП), розробленого Р. Фішером розглядають значення випадкових
величин Х1, Х2, ..., Х3, що отримані при
проведенні дослідів і використовують їх для визначення невідомого параметра а.
Якщо щільність розподілу  (х, а)
залежить від параметра а, то в ММП задаються правдоподібною функцією, виходячи
з того, що всі Х1 незалежні. Сутність ММП полягає в тому, що за
якісну оцінку параметра а беруть таке значення аргументу, яке приводить функцію
L до максимуму. Рівняння розв'язують
за умови (х, а)
залежить від параметра а, то в ММП задаються правдоподібною функцією, виходячи
з того, що всі Х1 незалежні. Сутність ММП полягає в тому, що за
якісну оцінку параметра а беруть таке значення аргументу, яке приводить функцію
L до максимуму. Рівняння розв'язують
за умови
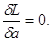
При цьому вибирають таке
визначення а, яке зводить функцію Ь до максимуму. Для спрощення функцію
правдоподібності заміняють логарифмом, тоді
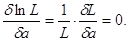
РОЗДІЛ 5. СТАТИСТИЧНА
ПЕРЕВІРКА ГІПОТЕЗ
1. Статистичні
дослідження рядів вимірів
Навколишнє середовище,
явища природи, закони фізики та інших наук вивчають шляхом випробувань, в
результаті яких отримують випадкові величини або статистичний ряд x1, x2, …, xn. Одночасно може досліджуватися
декілька явищ. При цьому отримують декілька статистичних рядів або сукупностей
випадкових величин.
Залежно від процесів, що
відбуваються при випробуваннях, кожен статистичний ряд підпорядковується тому
чи іншому закону розподілу. Його можна визначити шляхом математичної обробки
вимірів.
Для отримання надійних
результатів і обгрунтованих рішень при математичній обробці результатів
експериментів необхідно знати закони розподілу статистичних рядів. Знання
закону розподілу необхідно і для застосування методів обробки вимірів.
Всяке передбачення про
закон розподілу випадкових величин називають статистичною гіпотезою.
Статистична перевірка
гіпотез полягає у визначенні закону розподілу результатів експериментів.
Висунуту гіпотезу називають нульовою гіпотезою.
В результаті статистичної
перевірки для нульової гіпотези визначають статистику Q. Перевірка нульової гіпотези базується на теорії надійних
інтервалів та способах перевірки статистичних гіпотез.
За принципом практичної
впевненості для висунутої нульової гіпотези визначають теоретичне значення
статистики Qq. Його визначають за таблицями різних
критеріїв перевірки по заданій імовірності p або рівнях значимості q = 1 - р. В разі, коли 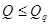 нульова гіпотеза
приймається. В протилежному випадку вона не підтверджується, тобто
відкидається. нульова гіпотеза
приймається. В протилежному випадку вона не підтверджується, тобто
відкидається.
Статистична перевірка
може виконуватися одним і більше критеріями (методами). При цьому може
виникнути дві помилки:
1. Бракування правильної
гіпотези. Уникнути її можна підвищенням значення ймовірності р або зниженням
рівня значності q.
2. Прийняття неправильної
гіпотези. Уникнути її можна застосуванням різних критеріїв перевірки.
Ймовірність прийняття
нульової гіпотези підвищується зі збільшенням кількості випробувань і практично
надійна, коли 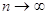 . Надійність
перевірки статистичної гіпотези висока при достатньо великій імовірності
бракування неправильної гіпотези. Важливе значення має і вибір критерію перевірки. . Надійність
перевірки статистичної гіпотези висока при достатньо великій імовірності
бракування неправильної гіпотези. Важливе значення має і вибір критерію перевірки.
При математичній обробці
геодезичних вимірів найбільш поширені такі перевірки статистичних гіпотез:
1. Визначення
систематичної (або постійної) похибки
Залежність від умов
експерименту може виконуватися такими способами:
а) систематичні похибки значно
спотворюють результат і можуть призвести до недоброякісних оцінок. Систематична
похибка може визначатися на компараторі розміром X і в результаті експериментів
буде отримано статистичний ряд x1, x2, …, xn
При обробці за формулою
визначають середнє арифметичне X і обчислюють різницю
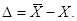
За формулою визначають
середню квадратичну похибку окремого виміру m та обчислюють середню квадратичну
похибку середнього арифметичного X за формулою
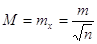
Обчислюють статистику
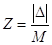
2. Визначення граничних
похибок.
При математичній обробці
результатів вимірів слід виключати із обробки грубі помилки. Методика
вимірювань дозволяє своєчасно виключити "промахи" при яких окремі
результати значно відрізняються від інших. Разом
з тим в статистичному ряду вимірів можуть бути результати вимірів, які досить
близькі між собою, але за вимогами точності або технології виконання робіт
будуть грубими. Тому поняття "груба помилка" досить умовне і залежить
від прийнятої надійної ймовірності.
При визначенні цільності
нормованого нормального закону розподілу користувалися нормованими похибками
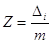
де 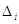 - похибка виміру; m - середня квадратична похибка. - похибка виміру; m - середня квадратична похибка.
При визначених умовах
вимірів завжди існує деяка гранична похибка 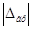 ,
яку не можуть перевищити випадкові похибки. Тоді за функцією Лапласа
нормованого нормального закону розподілу можна визначити інтервал zg, залежність від рівня значності q. ,
яку не можуть перевищити випадкові похибки. Тоді за функцією Лапласа
нормованого нормального закону розподілу можна визначити інтервал zg, залежність від рівня значності q.
2. Перевірка закону
розподілу статистичних рядів
Важливе значення
при математичній обробці геодезичних вимірів має знання закону розподілу
результатів або похибок вимірів. Найкращі оцінки отримують, коли ряд вимірів підпорядковується
нормальному закону розподілу. Однак, практично комплекс умов постійно дещо
змінюється. В наслідок цього виникає відхилення закону розподілу результатів
вимірів від теоретичного значення функцій розподілу.
Практично на основі тих
чи інших відомостей висувають припущення або ("нульову") гіпотезу про
вид закону розподілу статистичного ряду, створеного за результатами вимірів.
Шляхом застосування різних критеріїв перевірки визначають, чи є допустимим
розходження між дослідним і теоретичним (передбачуваним) законом розподілу.
Враховуючи, що результати геодезичних вимірів, як
правило, підпорядковуються нормальному закону розподілу при дотриманні
"комплексу умов" або вимог нормативно-технічної документації,
розглянемо ряд критеріїв повірки відповідності нормальному закону розподілу
результатів вимірів:
1. Перевірка по асиметрії
і ексцесу
Гіпотезу про нормальний
закон розподілу статистичного ряду називають нульовою або основною. Маємо
статистичний ряд x1, x2, …, xn і висунута гіпотеза, що він
підпорядковується нормальному закону розподілу (НЗР). За формулами можна
визначити числові характеристики НЗР: математичне сподівання або середнє
арифметичне, дисперсію, середню квадратичну похибку, асиметрію Sk та ексцес Еk.
Скористаємося тим, що
асиметрія Sk та ексцес Еk є числовими
характеристиками, що характеризують ступінь відхилення досліджуваного розподілу
від теоретичного НЗР. Вони, як і інші параметри НЗР є випадковими величинами, а
тому можуть відхилятися від нуля.
Мірою точності асиметрії
та ексцесу є дисперсії
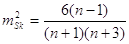
При великій
кількості вимірів
відповідно маємо
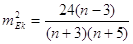
При великій
кількості вимірів маємо:
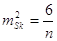 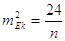
2. Критерій Колмогорова
Це найбільш простий
критерій перевірки гіпотези про нормальний закон розподілу. Використовується
різниця D між статистичною інтегральною
функцією розподілу 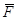 (z) і відповідною
теоретичною функцією розподілу F(z). (z) і відповідною
теоретичною функцією розподілу F(z).
При невеликій
кількості вимірів 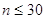 для
статистичного розрахунку обчислюють: середнє арифметичне для
статистичного розрахунку обчислюють: середнє арифметичне  , відхилення , відхилення  , за формулою Бесселя
середню квадратичну похибку m. Далі обчислюють нормовані похибки , за формулою Бесселя
середню квадратичну похибку m. Далі обчислюють нормовані похибки 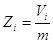 і
складають зростаючий ряд Zmin, Z1, Z2, … Zmax. і
складають зростаючий ряд Zmin, Z1, Z2, … Zmax.
3. Критерій x2 (Пірсона)
В математичній статистиці
його вважають найбільш строгим і надійним критерієм погодження нульових
гіпотез. Він забезпечує мінімальну ймовірність виникнення похибок 2-го роду.
Розрахунки в критерії
Пірсона аналогічні критерію Колмогорова і пов'язані з групуванням нормованих
похибок. Слід пам'ятати, що при групуванні похибок в кожному інтервалі їх
повинно бути не менше п'яти. Тому крайні інтервали можна штучно об'єднувати
(збільшувати). Число інтервалів повинно бути не менше чотирьох.
Критерієм перевірки
нульової гіпотези є статистика
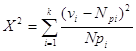 , ,
де N= [vi] - число всіх вимірів, pi - теоретичне значення ймовірності вибраних
інтервалів вибирається із таблиць.
В критерії Пірсона
доведено, що при нормальному розподілі похибок вимірів статистика X2 має X2 - розподіл з числом
ступенів вільності k = n – 1.
Критична область для
нульової гіпотези буде
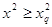
де %д - вибирається із
таблиць дод. 9 за заданими д\ і г = & — З, &- кількість інтервалів.
2. Розподіл
імовірностей випадкових похибок
Результати вимірів е
випадковими оскільки передбачити їх величину неможливо. Тоді і їх похибки
будуть випадковими і для них можна вказати лише межу, в яких вони змінюються
згідно з першою властивістю.
Неперервні випадкові
похибки можна характеризувати законом розподілу, як об'єктивно існуючим
зв'язком між випадковими величинами і їх імовірностями.
При багаторазових
випробуваннях закон розподілу ряду істинних випадкових похибок можна
характеризувати функціями:
1. Інтегральною функцією
розподілу
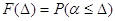 ( (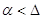 ) )
2. Функцією щільності
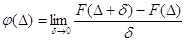
де 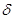 - приріст випадкової
похибки - приріст випадкової
похибки 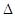 . .
Звернемося до постулату
Гаусса, згідно з яким найбільш імовірним значенням шуканої величини є середнє
арифметичне Із результатів повторних вимірювань. Скористаємося теоремою:
Якщо випадкові похибки
відповідають постулату Гаусса, то законом розподілу випадкових похибок буде
нормальний закон. В методі максимальної правдоподібності Фішера також доведено,
що для нормального закону розподілу випадкових величин оцінкою параметра 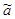 є середнє арифметичне. є середнє арифметичне.
Функція щільності
нормального розподілу випадкових похибок визначиться за формулою
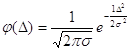
Для нормованих
похибок 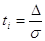 отримаємо отримаємо
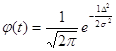
3. Числові
характеристики рівноточних вимірів
Рівноточними,
називають виміри, дисперсії яких рівні між собою, тобто 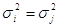 . Тому рівноточні виміри можна виразити
статистичним рядом . Тому рівноточні виміри можна виразити
статистичним рядом
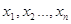 ( (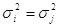 ) )
Якщо невідоме істинне
значення вимірюваної величини Х, то
необхідно знайти значення близьке до істинного. Його називають дійсним, або
ймовірним значенням виміряної величини. Воно може бути прийнятим, коли точність
вимірів задовольняє поставленим вимогам, або - відхилене. Тому постає задача
обчислення за результатами вимірів показників як розміру шуканої величини, так
і її точності, їх називають числовими характеристиками. В теорії похибок
вимірів до числових характеристик відносять:
1. Середнє арифметичне
Використаємо ряд вимірів.
Якщо відоме істинне значення вимірюваної величини X, то визначимо ряд істинних
похибок
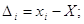
Складемо їх і поділимо на
n
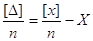
За четвертою властивістю
компенсації випадкових похибок 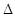 ліва ліва
частина формули
наближається до нуля при 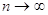 .
Позначимо середнє арифметичне .
Позначимо середнє арифметичне
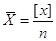
Тоді отримаємо ймовірне
співвідношення 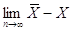
Принцип арифметичного
середнього показує, що при нескінченній кількості вимірів і відсутності
систематичних похибок просте арифметичне середнє наближається до істинного
значення.
Це означає, що середнє
арифметичне X буде найбільш точним, або ймовірніш значенням виміряної величини.
Як виміри, так і похибки вимірів при
дотриманні "комплексу умов" належать нормальному закону розподілу.
Тоді і за методом ММП Фішера доведено, що середнє арифметичне буде найбільш
близьким до істинного.
Практично число вимірів
обмежене, тому і обчислене середнє арифметичне буде випадковою величиною, яка
може приймати значення в деякому інтервалі, який залежить від числа вимірів та
прийнятої довірчої ймовірності.
2. Середня квадратична
похибка окремого виміру
Теоретично мірою точності
вимірів є дисперсія 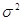 . За результатами статистичної обробки рядів вимірів
визначають емпіричну (або статистичну) дисперсію m2 . За результатами статистичної обробки рядів вимірів
визначають емпіричну (або статистичну) дисперсію m2
За ММП Фішера доведено,
що коли статистичний ряд, підкоряється нормальному закону розподілу, ефективною
точності є дисперсія
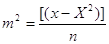
Оскільки розмірність
дисперсії ("в квадраті"), то за міру точності приймають емпіричний
стандарт або середню квадратичну похибку

де 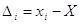 - істинні похибки. - істинні похибки.
Її називають
похибкою Гаусса.
Якщо невідоме істинне значення
вимірювальної величини, то використовуємо різниці
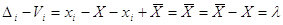 , ,
де 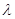 - систематична похибка. - систематична похибка.
Коли число
вимірів дорівнює n, із формули отримаємо:
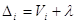 , , 
Зведемо вираз до
квадрату і підсумуємо 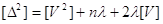
Якщо в формулі
взяти суму ймовірних похибок V, отримаємо:

Оскільки середнє арифметичне за формулою
дорівнює 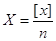 , то в формулі отримаємо: , то в формулі отримаємо:
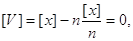
або 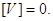
Формула
використовується і для контролю обчислення ймовірних похибок V.
Тоді формула
зведеться до вигляду
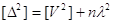
Істинна похибка 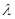 простої арифметичної
середини обчислюється за формулою: простої арифметичної
середини обчислюється за формулою:
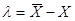 або або 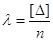 . .
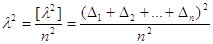
Згідно з
четвертою властивістю випадкових похибок
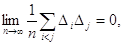
з врахуванням
попередніх формул отримаємо
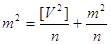
Остаточно
отримаємо формулу Бесселя для визначення середньої квадратичної похибки виміру
за ймовірними похибками
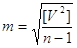
3. Середня квадратична
похибка арифметичної середини
Запишемо 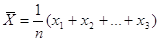
Оскільки виміри
рівноточні, тобто 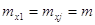 , а часткові
похідні , а часткові
похідні 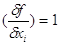 , то за формулою отримаємо
дисперсію середнього арифметичного , то за формулою отримаємо
дисперсію середнього арифметичного
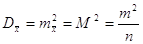
Тоді середня квадратична
похибка арифметичного середнього арифметичного буде
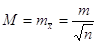
Додатково обчислюють:
4. Середню квадратичну
похибку середньої квадратичної похибки
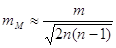
5. Середню квадратичну похибку
середньої квадратичної похибки арифметичного середнього

Для оцінки точності похибок вимірів використовують
інші критерії.
6. Середню похибку 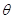 , як середнє арифмитичне із
суми абсолютних випадкових значень похибок, тобото , як середнє арифмитичне із
суми абсолютних випадкових значень похибок, тобото
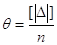
7. Середню похибку r. Її визначають в середині зростаючого ряду
складеного із абсолютних значень похибок вимірів. Тоді ймовірність серединної
похибки буде
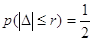
Середня квадратична похибка виміру m має зв’язок середньою
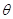 та серединною r похибками та серединною r похибками
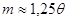 ; ;
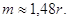
8. Абсолютні похибки. До них
належать: середня квадратична (m),
середня квадратична арифметичного середнього (М), середня (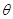 ), серединна (r), істинна ( ), серединна (r), істинна (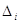 ), ймовірна (Vi) і гранична ( ), ймовірна (Vi) і гранична ( ) )
9. Відносні похибки. Відношення
абсолютної похибки до значення виміряної величини називають відносною похибкою.
Назва відносної похибки відповідає
назві абсолютної похибки, наприклад:
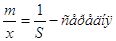 квадратична відносна похибка; квадратична відносна похибка;
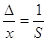 - істинна відносна похибка. - істинна відносна похибка.
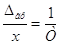 - гранична відносна похибка тощо. - гранична відносна похибка тощо.
Оцінка точності вимірів за
допомогою середніх квадратичних похибок m порівняно з середньою та серединною похибками
має переваги:
1. Обгрунтованості: ймовірність  , тобто при умовах коли
число вимірів прямує до нескінченності, середня квадратична похибка прямує до
абсолютного значення стандарту. , тобто при умовах коли
число вимірів прямує до нескінченності, середня квадратична похибка прямує до
абсолютного значення стандарту.
2. Ефективності: 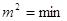 , тобто значення дисперсії
буде мінімальним. , тобто значення дисперсії
буде мінімальним.
3. На величину середньої квадратичної
похибки m вплив
більших за абсолютним значенням похибок 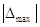 найбільший. найбільший.
4. Середня квадратична похибка m зв’язана з граничною
похибкою відношенням
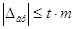 , ,
де t – вибирається із таблиць розподілу Лапласа або Стюдента залежить від
надійної ймовірності p та кількості
вимірів n.
5. Середня квадратична похибка
визначається достатньо надійно при обмеженій кількості вимірів.
4. Числові
характеристики нерівноточних вимірів
В практиці геодезичних вимірювань
може відчутно порушуватися "комплекс умов": виміри виконують приладами
різної точності або різними методами, значно змінюються зовнішні умови
(температура, вологість тощо) чи інші чинники. Тоді дисперсії таких
вимірів значно відрізняються між собою (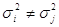 )
і їх називають нерівноточиними. Нерівноточні виміри можна
виразити статистичним рядом )
і їх називають нерівноточиними. Нерівноточні виміри можна
виразити статистичним рядом
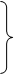
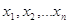 , ,
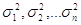 ( (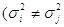 ) )
Задача виникає, коли за
результатами нерівноточних вимірів однієї і тієї величини необхідно визначити
найбільш надійне значення виміряної величини
і виконати оцінку точності вимірів за допомогою числових характеристик.
В теорії похибок вимірів
до числових характеристик нерівноточних вимірів відноситься:
1. Вага вимірів.
Розглянемо статистичний ряд нерівноточних вимірів, який будемо характеризувати
емпіричними дисперсіями 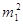
 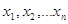 , ,
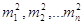 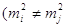 ) )
Введемо величини — 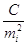 , обернено пропорційні
квадратам середніх квадратичних похибок (емпіричних
дисперсій ) і позначимо , обернено пропорційні
квадратам середніх квадратичних похибок (емпіричних
дисперсій ) і позначимо
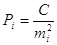
де С - постійний умовно
прийнятий коефіцієнт такої величини, щоб значення ваги рі було
ближче до одиниці.
Величину рі
називають вагами нерівноточних вимірів. Тоді нерівноточні виміри можна
характеризувати статистичним рядом
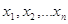 , ,
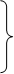 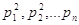 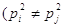 ) )
Якщо дисперсія є мірою
абсолютної точності результату, то вага є мірою відносної точності.
Вага вказує наскільки
точність одного виміру більш або менш точна відносно іншого в ряду вимірів.
Практично в більшості
випадків невідома дисперсія  або
середня квадратична похибка вимірів m. Ваги вимірів обчислюють за
наближеними формулами або
середня квадратична похибка вимірів m. Ваги вимірів обчислюють за
наближеними формулами
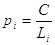 ; ;
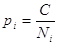 ; ;
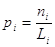 , ,
де Li – довжина лінії, ходу або
полігону;
Ni – кількість виміряних величин;
ni – кількість вимірів однієї і
тієї величини (число прийомів).
Аналогічно коефіцієнт С
вибирають так, щоб ваги pi за величиною були близькі до одиниці для зручності обчислень.
В практичних розрахунках
часто використовують приведені ваги
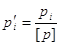 , ,
де 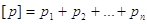 , тоді , тоді 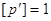
Ряд нерівноточних вимірів
можна звести до рівноточного, якщо кожен вимір помножити на величину 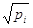 . Статистичний ряд . Статистичний ряд
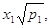 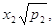 ..., ...,
 - буде рівноточним. - буде рівноточним.
2. Загальне середнє
арифметичне
Припустимо, що в
результаті вимірів однієї величини отримано статистичний ряд нерівноточних
результатів
 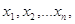
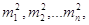 ( (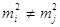 ) )
Найкращі оцінки отримують
тоді, коли виміри х1, або їх похибки 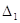 ,
підкоряються нормальному закону розподілу. Перейдемо до нормованих похибок ,
підкоряються нормальному закону розподілу. Перейдемо до нормованих похибок
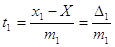 ; ;  ; ; 
де X- істинне значення
вимірюваної величини.
Функція щільності
нормованого нормального закону розподілу визначається за формулою
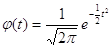
Числові характеристики
визначаються за результатами всіх вимірів. Тоді функція щільності сумісного
розподілу ряду випадкових величин 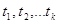 буде буде

Найбільш надійне значення
шуканого параметра t для
нерівноточних вимірів буде відповідати максимальному значенню функції 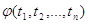 . Із
формули видно, що це відбудеться за умови, коли показник степеня буде
мінімальним, тобто . Із
формули видно, що це відбудеться за умови, коли показник степеня буде
мінімальним, тобто
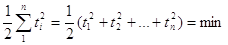
З врахуванням попередньої формули отримаємо
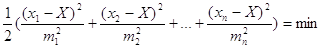
Для визначення екстремуму
функції візьмемо першу похідну за перемінними х1, прирівняємо до нуля і отримаємо
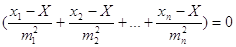
Умовно помножимо їх на довільне число С, отримаємо
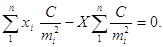
Оскільки 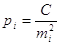 , то
отримаємо , то
отримаємо
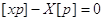
Ймовірно 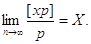
Це означає, що частка 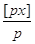 при
необмеженій кількості вимірів прямує до
істинного значення. Його називають загальним середнім арифметичним при
необмеженій кількості вимірів прямує до
істинного значення. Його називають загальним середнім арифметичним
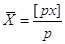
або 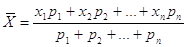
В разі рівноточних
вимірів 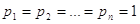 . Тоді формула . Тоді формула 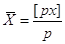 зводиться до простої арифметичної
середини зводиться до простої арифметичної
середини  , тому цю формулу і називають загальною середньою арифметичною. , тому цю формулу і називають загальною середньою арифметичною.
3. Середня квадратична
похибка одиниці ваги
Нерівноточні виміри
характеризують дисперсіями 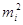 або
мірою відносної точності pi. Умовно із ряду нерівноточних вимірів виберемо результат такого виміру xk, вага якого буде дорівнювати
одиниці, тобто або
мірою відносної точності pi. Умовно із ряду нерівноточних вимірів виберемо результат такого виміру xk, вага якого буде дорівнювати
одиниці, тобто 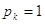 . Дисперсію цього результату позначимо через . Дисперсію цього результату позначимо через 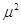 . Тоді . Тоді
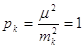 , ,
або середня квадратична
похибка одиниці ваги буде дорівнювати:
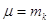 .
Оскільки .
Оскільки 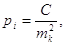 то то 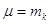 ,
або ,
або
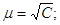
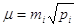
Тоді середня квадратична
похибка будь-якого виміру визначиться за формулою

При р = 1, 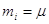 - тобто середня квадратична похибка
одиниці ваги є мірою точності того результату виміру, вага якого дорівнює
одиниці. - тобто середня квадратична похибка
одиниці ваги є мірою точності того результату виміру, вага якого дорівнює
одиниці.
Визначимо середню
квадратичну похибку одиниці ваги:
а) при заданому істинному
значенні виміряної величини
В результаті
нерівноточних вимірювань однієї і тієї ж величини X отримано статистичний ряд
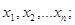
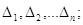
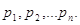
де  — істинні похибки
нерівноточних вимірів, — істинні похибки
нерівноточних вимірів, 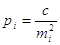 - вага
вимірів. - вага
вимірів.
Зведемо ряд нерівноточних похибок
вимірів до рівноточного ряду
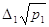 , , 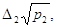 …, …, 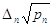 (i = l,n) (i = l,n)
Оскільки ряд даний є рівноточним і підкоряється
нормальному закону розподілу, то за формулою Гаусса можна визначити середню
квадратичну похибку m вимірів. Для
виміру вага якого дорівнює одиниці р = 1. Це буде середня квадратична похибка одиниці ваги 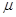 , або , або
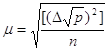 , або , або
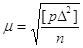 . .
б) при обчисленому
загальному середньому арифметичному
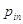 , , 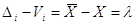 (i = l,n) (i = l,n)
де 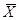 — загальне середнє
арифметичне; — загальне середнє
арифметичне;
X - істинне значення
вимірюваної величини.
Зробимо перетворення
Тобто, при нерівноточних
вимірах і наявності істинних похибок 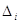 ,
систематична похибка ,
систематична похибка 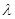 , визначиться за
формулою , визначиться за
формулою
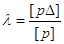
Для спрощення доказів
складемо ряд ймовірних похибок
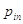 , , 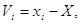 (i = l,n) (i = l,n)
Оскільки 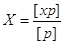 , то , то
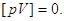
З формули ряд імовірних
похибок теж є нерівноточним. Як і в попередньому випадку зведемо їх до
рівноточного вигляду
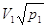 , , 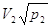 ..., ..., 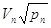 , (i = l,n) , (i = l,n)
Оскільки ряд є
рівноточним і за умовами підкоряється нормальному закону розподілу, то за
формулою Бесселя визначимо середню квадратичну похибку m. Для виміру, вага якого буде дорівнювати одиниці (р = 1)
вона буде дорівнювати середній квадратичній похибці одиниці ваги, тобто 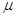
 або або
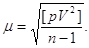
4. Середня квадратична
похибка загального середнього арифметичного
Формулу загального середньоарифметичного
отримаємо у вигляді

Дисперсія функції F (х) при отримаємо 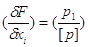 , отримаємо , отримаємо
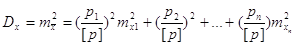
Середня квадратична похибка загального
середнього арифметичного при нерівноточних вимірах визначиться за формулою

Додатково обчислюють:
5. Середню квадратичну
похибку середньої квадратичної похибки одиниці ваги
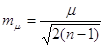 . .
6. Середню квадратичну
похибку середньої квадратичної похибки загального середнього арифметичного
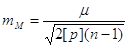 . .
|