Курсовая работа: Стандартизация измерения рН в неводных средах. Методы определения рН стандартных буферных растворов
Курсовая работа: Стандартизация измерения рН в неводных средах. Методы определения рН стандартных буферных растворов
МИНИСТЕРСТВО
НАУКИ И ОБРАЗОВАНИЯ УКРАИНЫ
ХАРЬКОВСКИЙ
НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
им. В.Н.
Каразина
Кафедра
физической химии
СТАНДАРТИЗАЦИЯ
ИЗМЕРЕНИЯ рН В НЕВОДНЫХ СРЕДАХ. МЕТОДЫ ОПРЕДЕЛЕНИЯ рН СТАНДАРТНЫХ БУФЕРНЫХ
РАСТВОРОВ
Курсовая работа
студентки III курса
химического
факультета
****************
ХАРЬКОВ
2008
СОДЕРЖАНИЕ:
ВВЕДЕНИЕ
1.Понятие pH
2.Кислотность неводных растворов
2.1.Шкала рНр
2.2 Единая шкала кислотности
2.3 Метод Михаэлиса. Шкала рНHAc Конанта и Хелла
2.4 Определение кислотности методом Гамметта
2.5Метод нормального потенциала Плескова
2.6.Применение средних
коэффициентов активности 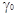 ионов
для оценки единой шкалы кислотности ионов
для оценки единой шкалы кислотности
2.7 Нахождение единой кислотности рА с помощью 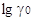 протонов протонов
3.Буферные растворы
3.1.Классификация
кислотно-основных буферных систем
3.2.Определение pH стандартных буферных растворов
ВЫВОД
СПИСОК ЛИТЕРАТУРЫ
РЕФЕРАТ
Данная курсовая работа
содержит 3 раздела, 35 страниц и 2 таблицы.
Целью работы является
изучение кислотности неводных растворов, методы ее определения и стандартизация
измерения, а также изучение методов определения pH стандартных буферных растворов.
В работе рассмотрено
несколько методов определения кислотности неводных растворов, а также
стандартных буферных растворов, проведено их сравнение в соответствии с допустимыми погрешностями измерения.
Ключевые слова: НЕВОДНЫЙ
РАСТВОР, КИСЛОТНОСТЬ, КОЭФФИЦИЕНТ АКТИВНОСТИ, ПОТЕНЦИАЛ, БУФЕРНЫЙ РАСТВОР.
РЕФЕРАТ
Курсова робота містить 3 розділи, 35 сторінок
та 2 малюнка.
Ціллю роботи є
вивчення кислотності неводних розчинів, методи її визначення та стандартизація
вимірювання, а також вивчення методів визначення рН стандартних буферних
розчинів.
В роботі
розглянуто кілька методів визначення кислотності неводних розчинів, а також
стандартних буферних розчинів, проведено їх порівняння відповідно до
припустимих похибок вимірювань.
Ключові слова:
НЕВОДНИЙ РОЗЧИН ,КИСЛОТНІСТЬ, ПОТЕНЦІАЛ, КОЕФІЦІЄНТ АКТИВНОСТІ, БУФЕРНИЙ
РОЗЧИН.
ABSTRACT
This term
paper consists of 3 sections, 35 pages and 2 pictures.
The aim of the
work is studying the acidity of nonaqueous solutions, methods of their determination,
standartization of their measuring, and also studying the methods of measuring
pH in standard buffer solutions.
In this work
are considered several methods of acidity measuring. They were compared in
accordance with acceptable errors.
Key words:
ACIDITY, ACTIVITY COEFFICIENT, POTENTIAL, BUFFER SOLUTION.
ВВЕДЕНИЕ
Сложность явлений, происходящих в растворах, а
также необходимость изучения растворов с широким диапазоном физических и химических
свойств растворителя неизбежно привлекали внимание исследователей к неводным
средам. Неводные растворители постепенно начали использовать не только для
научных исследований, но и в практической деятельности. Они широко применяются
в аналитической практике для улучшения условий титрования. Неводные
растворители часто используются в химической, фармацевтической,
нефтеперерабатывающей промышленности, в промышленности высокополимеров и в
других отраслях народного хозяйства.
Быстрыми
темпами осуществляется переход к проведению процессов органического синтеза в
неводных средах. Замена воды органическими растворителями и переход на
замкнутые системы производства позволяет, во-первых, резко интенсифицировать
химические процессы, во-вторых, упрощает решение проблем, связанных с очисткой
сточных вод и с нарастающей нехваткой пресной воды. Поэтому понятен интерес к
методам оценки кислотности неводных растворов и растворов в смешанных
растворителях.
Используемые
в качестве эталонов для измерений буферные растворы введены давно. Стандартные
буферные растворы используются для калибровки приборов, поэтому точность
определения кислотности этих растворов должна быть высокой.
1.Понятие pH
Водородный
показатель, pH —
это мера активности(в случае
разбавленных растворов совпадает с концентрацией) ионов водорода в растворе,
количественно выражающая его кислотность, вычисляется как отрицательный
десятичный логарифм концентрации водородных ионов,
выраженной в молях на литр:
![\mbox{pH} = -\lg \left[ \mbox{H}^+ \right]\!](/image/16066_3_1.png) (1)
(1)
Зависимость
громадного количества химических, биохимических, природных, технологических и
многих других процессов от величины рН стимулирует развитие теории и техники
измерения этого показателя.
Трудно
отыскать такую область науки, технологии и химии растворов, в которой не
использовалась бы величина рН. Шкала рН была предложена датским химиком
Зеренсеном. Изучая биохимические реакции, в частности гидролиз пепсина и
усвоение протеинов в кислотно-солевых смесях, Зеренсен в 1909 году обнаружил
их чрезвычайно сильную зависимость от изменения концентрации ионов водорода.
Он нашел, что эффективная концентрация ионов водорода, непосредственно
воздействующих на процесс, изменялась в широком диапазоне концентраций и часто
оказывалась непривычно малой величиной. Для удобства Зеренсен предложил
записывать ее в экспоненциальной форме сН + = 10-р
= 1/10р. Позднее символ -р был заменен обозначением рН.
На современном языке р понимают как оператор р = -lg, таким образом, pH = -lg[H+]. Именно так трактуется
это обозначение в Номенклатурных правилах Международного союза по теоретической
и прикладной химии (International Union for Pure and Applied Chemistry), ИЮПАК.
2.Кислотность неводных растворов.
2.1.Шкала рНр
Важным вопросом является определение рН в
неводных и смешанных растворителях. Этот вопрос имеет практическое значение,
так как в пищевой промышленности, промышленности пластмасс, фото- кино- промышленности
и других отраслях промышленности широко используют измерения рН в неводных
растворах.
При определении рН в неводных растворах делается
еще большее количество ошибок, чем при определении рН в водных растворах.
При решении проблемы о кислотностях неводных
растворов следует поставить два вопроса. Как поступать при сравнении
кислотности двух растворов в одном и том же растворителе? Как поступать при сравнении
кислотности растворов в двух разных растворителях? Эта задача отличается
принципиально от задачи сравнения между собой кислотности в пределах одного
растворителя.
Очень часто намерении pН в неводных растворах производят
по отношению к водному каломельному электроду, потенциал которого определяется
по водному стандарту. При этом фактически измерения сводят к измерению э.д.с
цепи:
Pt(H2) | стандартный | исследуемый | Pt(H2) (2.1.1)
р-р в воде р-р в
неводн р-ле
Таким образом значения рН неводных
растворов не могут быть получены путем непосредственного сопоставления
потенциалов индикаторных электродов в водных и неводных растворах, а
следовательно, и рН-метр, калиброванный по водным стандартам, не может дать
правильных значений рН неводного раствора.

Рис. 1. Шкала рНр и шкала раН
в различных растворителях.
По вопросу о стандартизации рН в неводных
растворах нет единого мнения. Тем не менее расширение этого вопроса становится
все более насущным в связи с широким распространением неводных растворителей, и
особенно их смесей с водой, в промышленности и аналитической практике.
Задача сравнения кислотности в пределах одного
неводного растворителя принципиально не отличается от задачи определения рН в
водных растворах. Величина рН определяется отрицательным логарифмом активности ионов
водорода в данном растворителе М:
pHp=-lga*=-lgc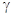 * *
т.е. отрицательным логарифмом произведения
концентрации ионов лиония
на соответствующий концентрационный коэффициент
активности. Коэффициент активности относится к бесконечно разбавленному
раствору в данной среде как стандарту.
Переходя от воды в неводному растворителю,
переходят от кислотности,
выраженной в концентрациях или активностях одного
иона - иона гидроксония, к кислотности, выраженном в концентрациях или активностях
другого иона – лиония. Действительно, в воде носителем кислотных свойств
является ион Н3О+. Когда по отношению к водному раствору
мы говорим, что его рН = 5, это значит, что активность ионов Н3О+
равна 10-5. В спиртовом растворе носителем кислотных свойств
являются ионы этоксония С2Н5ОН2+, в
аммиаке носителем кислотных свойств — соответственно ионы аммония NH4+ и т. д.
При оценке рН растворов в пределах одного
растворителя следует учитывать протяженность шкалы рН: в.воде вся шкала рН
равна 14,0, но в этиловом спирте 19,3; в муравьиной кислоте. 6,1 и т. д. (рис.
1)
Стандартизация рН в неводных растворах может быть
выполнена так же как и в водных растворах, т. е. путем изготовления стандартных
растворов в том же растворителе, что и исследуемый раствор. Однако в этом
случае возникает ряд затруднений. Например, коэффициенты активности сильных кислот
значительно больше отличаются от единицы, чем в водных растворах; сильные в
воде кислоты становятся в неводных растворах слабыми; хуже растворимы соли; значительно
меньше имеется данных о коэффициентах активности.
В настоящее время единственным веществом, с
помощью которого может быть произведена стандартизация рН в неводных растворах,
является хлористый водород, так как для него имеются данные о коэффициентах активности
в большинстве широко используемых растворителей и в их смесях с водой. В
качестве электрода сравнения при измерениях в неводных растворах может быть
использован хлорсеребрянный электрод в растворе НCl, который вполне пригоден
для измерений в ряде чистых неводных растворителей и их смесях с водой.
Измеренная по отношению к стандарту в данном
растворителю рН не является абсолютном мерой кислотности неводного раствора и
может быть использована для характеристики кислотности только в пределах
данного растворителя. Это следует из того, что начало шкалы кислотности раНр
=0 не соответствует равенству абсолютных активностей ионов водорода во всех растворителях.
Величины раН нейтральных растворов в разных растворителях не
совпадают друг с другом, так как протяженность шкал, зависящая от ионного
произведения растворителя, различна. В верхней части рис. 1 в качестве примера
приведены шкалы рНр в воде и не которых неводных средах. В воде
шкала рН изменяется от 0 до 14; нейтральным раствором называется раствор с рН =
7. Если раствор имеет рН=0, это раствор кислоты с активностью ионов Н+,
равной единице; если раствор имеет рН = 14, это раствор щелочи с активностью
ионов ОН--, равной единице, но это не значит, что не может быть
растворов в воде с рН меньше нуля и больше 14.
Раствор, у которого рН =15, означает раствор
щелочи с активностью, равной 10, растворы с рН=-1 являются растворами кислоты
с активностью, равной 10.
В воде между одноактивным раствором кислоты и
одноактивным раствором щелочей изменение рН равно 14, это является следствием
того, что ионное произведение воды равно 10-14. В метиловом спирте
ионное произведение равно 10-16,5. Это значит что между одноактивным
раствором щелочи и одноактивным раствором кислоты изменение рН будет составлять
16,5 единицы. У нейтрального раствора рН будет не 7, как в воде, а 8,3.
Этиловый спирт имеет шкалу протяженностью 19,3 единицы; следовательно, рН
нейтрального раствора будет составлять 9,7. В аммиаке шкала имеет протяженность
32,7 единицы и нейтральный раствор в нем будет иметь рН = 16,3.
Таким образом, нужно иметь в виду, как относится
величина рН данного раствора к рН нейтрального раствора.
Поэтому предложено отмечать показатель рН
индексом, равным рН нейтральной точки. В воде рН-следует отмечать индексом 7 -
рН7, в этиловом спирте индексом 9,7 — рН9,7 и
т. д.
Мы уже говорили о невозможности определения рН в
цепях, содержащих водный и неводный растворы. Измерение рН должно
производиться в цепи, содержащей только один растворитель; стандартный и
измеряемый растворы должны быть в одном и том же растворителе. При измерении рН
в спирте стандартные растворы должны быть также спиртовыми.
Это положение не исключает практического
применения водного стандарта. Можно пользоваться водным каломельным электродом
и в этих случаях, но его потенциал следует измерять по отношению к неводному
стандарту. В принципе стандартизация шкалы рНр всегда должна быть
произведена по отношению к неводному раствору ионов водорода.
2.2 Единая шкала кислотности
Для решения ряда практически важных вопросов
возникает необходимость сопоставления кислотности растворов в различных
растворителях, приведение значений рНр к единому началу отсчета.
Можно было бы полагать, что измерения, произведенные на рН-метре,
откалиброванном по водным стандартам, должны давать значения рН по отношению к
единому стандарту, так как электрод сравнения остается неизменным и измеряемая э.д.с
представляет собой разность потенциалов электродов, обратимых но отношению к
ионам водорода, опущенных в стандартный водный и исследуемый неводный
растворы. Однако, как уже говорилось, наличие фазового потенциала не позволяет
находить значения раНр, отнесенные к единому водному
стандарту.
Как же сравнивать кислотность в двух различных
растворителях? Как решить вопрос о том, какой раствор кислее — водный с рН = 3
или спиртовой с тем же рНр — 3? Вопрос о сопоставлении кислотности
представляет большие трудности как принципиального, так и экспериментального
характера. Эти затруднения пытались решать разными методами. Самой правильной
является постановка вопроса о кислотности неводных растворен Бренстеда.
Бренстед предлагает во всех растворах считать мерой кислотности абсолютную
активность протона или величину, ей пропорциональную — химический потенциал
протона:
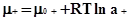 (2.2.1) (2.2.1)
Принципиально определение абсолютной активности
протона вполне возможно. Константа собственной кислотности кислоты равна
активности протона, умноженной на активность основания и деленной на активность
кислоты. При этом речь идет об абсолютной активности, т. е. об активности,
отнесенной к единому стандартному состоянию:
Ka=aH+*aB/aA (2.2.2)
Заменяя абсолютные активности произведениями
активностей, отнесенных к бесконечно разбавленному раствору в данной среде М, и
единых коэффициентов активности ץ 0 получим выражение
Ka=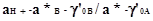 (2.2.3) (2.2.3)
Откуда: aH+=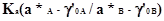 (2.2.4) (2.2.4)
Из этого выражения вытекает, что если бы можно
было действительно найти константу собственной кислотности какой-то кислоты в
вакууме и  и и  , то можно было бы
определить активность протона. Величины , то можно было бы
определить активность протона. Величины 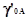 и и
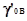 можно определить
экспериментально. Можно найти, сколько в данном растворителе кислоты и сколько
основания, т. е. установить, в какой степени данная кислота продиссоциирована,
найти концентрационные коэффициенты активности можно определить
экспериментально. Можно найти, сколько в данном растворителе кислоты и сколько
основания, т. е. установить, в какой степени данная кислота продиссоциирована,
найти концентрационные коэффициенты активности 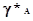 и и
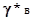 и найти активность а*. и найти активность а*.
Основные затруднения состоят в определении единых
коэффициентов активности 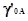 кислоты
и соответственно основания кислоты
и соответственно основания 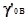 . .
Мерой этих абсолютных коэффициентов активности является
энергия переноса вещества из вакуума в данную среду, т. е. энергия их
сольватации.
Следовательно, для того чтобы использовать в
качестве единой меры кислотности активность протона, нужно знать собственную
константу кислотности кислоты и знать энергии переноса кислоты и основания из
вакуума в данную среду.
В настоящее время эти величины известны только
очень приближенно, поэтому такой путь определения истинной активности протона
еще не может быть осуществлен.
Если известно протонное сродство (работа
присоединения протона к данному веществу в вакууме), то из него всегда можно
вычислить константу собственной кислотности. Следовательно, некоторые
возможности определения активности протона этим путем уже намечаются. Если
раньше константа собственной кислотности была фиктивной мерой силы кислоты, то
сейчас ее можно рассматривать как реальную меру. Применение этого метода затруднено
только недостаточной точностью в определении протонного сродства и 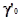 . .
2.3 Метод Михаэлиса. Шкала рНHAc Конанта и Хелла
Трудности в определении активности протона
привели к тому, что было предложено много других методов оценки кислотности в
неводных растворах. Первой была попытка Михаэлиса и Митцутани, которые предложили
оценивать кислотность в неводных растворах, измеряя э. д. с. цепи, включающей
диффузионный и фазовый потенциал
Pt(H2) | H+ в воде | | Н+ в М | Pt(H2) (2.3.1)
и
на основании э. д. с. этой цепи вычислять кислотность. Если бы не было
дифузионного, и особенно фазового, потенциалов, то эту цепь, действительно,
можно было бы применять для оценки кислотности, потому что потенциалы
электродов различаются настолько, насколько различаются между собой активности
ионов лиония в этих двух растворах. На самом доле э. д. с. этой цепи
определяется не только разностью активности ионов лиония, но и величиной
фазового потенциала, который обычно направлен против потенциала, обусловленного
различной активностью протонов. Поэтому метод Михаэлиса и Митцутани непригоден
для оценки абсолютной кислотности.
Конант и Хелл, исследуя кислотность в уксусной
кислоте как растворителе, предложили измерять кислотность в такой цепи:
Ptхлоранил| Н+ в уксусной кислоте|| KCl в воде| Hg2Cl2,Hg (2.3.2)
Хлоранил представляет собой эквимолекулярную
смесь С6(ОН)2С14 и С6С1402.
С помощью этого вещества можно измерять кислотность очень кислых растворов. В
воде потенциал хлоранилового электрода против каломельного равен 0,418 В.
Конант и Хелл для своей цели приняли, что потенциал хлоранилового электрода
против каломельного равен не 0,418, а 0,566. Они считали, что разница на 0,148
В соответствует фазовому потенциалу, который возникает на границе
уксусной кислоты и водного раствора, и изменению нормального потенциала
хлоранилового электрода. Но это предположение произвольно. Эта разница очень
плохо оправдана. Конант и Хелл приняли ее на том основании, что в результате
введения поправки константа диссоциации пиридина в уксусной кислоте равна
константе диссоциации у уксусной кислоты в воде. Равенство констант принято ими
на основании изучения электропроводности растворов. Однако это предположение сомнительно.
Кислотность, определенную по Конанту и Хеллу, принято
обозначать pHHAc.
2.4 Определение кислотности методом Гамметта
Основываясь на том, что, как свидетельствуют
экспериментальные данные, константы кислотности оснований (катионных кислот) сравнительно-мало
изменяются при переходе от растворителя к растворителю, Гамметт предложил
оценивать кислотность любых растворов по степени превращения индикатора
основания в его ионную форму.
Известно, что величина рН водных растворов может
быть определена про помощи индикаторов. В основе индикаторного метода лежит уравнение
pH=pK+lg(aAi/aHAi) (2.4.1)
где aAi и aHAi активности ионной и
молекулярной формы индикатора.
В случае, если индикатором является основание,
уравнение приобретает вид:
pH=pK+lg(aBi/aBHi)
(2.4.2)
Различия в окраске основания и катионной кислоты,
соответствующей этому основанию, или кислоты и аниона этой кислоты позволяют
установить кислотность. Метод основан на том, что по окраске оценивают
концентрацию кислой и основной форм индикатора. Сравнение окраски в данном
растворе с окраской раствора, содержащего предельную форму индикатора в
условиях, когда индикатор полностью превращен либо в кислоту, либо в
основание, производится в колориметре. Особенно удобны для этих целей
одноцветные индикаторы, у которых одна из форм окрашена, а другая не окрашена.
Не будем подробно останавливаться на методике
индикаторного определения рН. Отметим только, что при правильном осуществлении
этот метод определения рН достаточно точен. Однако применение индикаторного
метода не исключает ошибок, связанных со стандартизацией рН. Кроме того,
индикаторный метод имеет ряд специфических ограничении, с которыми следует
считаться.
Во-первых, если раствор содержит окислители или
восстановители, то пользоваться колориметрическим методом следует с осторожностью,
так как при этом может произойти окисление индикатора, и окраска (и ее
интенсивность) будет изменяться не за счет изменения рН, а за счет окисления
индикатора. К тому же многие вещества одновременно являются кислотно-основными
и окислительно-восстановительными индикаторами и реагируют на наличие в
растворах окислительно-восстановительных систем.
Во-вторых, индикаторы ограниченно применимы в
небуферных системач, так как каждый индикатор — это или кислота., или
основание, и прибавление их к небуферным системам создает определенную
кислотность. В этих случаях фактически измеряется та величина рН, которая
создалась в результате растворения индикатора.
В-третьих, окраска индикатора изменяется в
зависимости от ионной силы раствора.
В-четвертых, многие индикаторы реагируют с
белками, поэтому в белковых системах, в биологических средах индикаторный
метод может при вести к так называемым белковым ошибкам.
Возвратимся к основному вопросу — к определению
единой кислот ности. Согласно Гамметту, окраска одного индикатора изменяется в
различных растворителях только в связи с изменением абсолютной кислотности
растворов, а константа индикатора основания в любом растворителе остается
неизменной. Соотношение основной и кислой форм индикатора изменяется только в
связи с изменением кислотности раствора. Свою функцию кислотности Гамметт
обозначает Н0, так как индикаторы основания не имеют электрического
заряда. По Гамметту
Н0=pKa+lg(cB/cBH+) (2.4.3)
где pKa - показатель константы диссоциации
индикатора как катионной кислоты в воде. Эта константа принимается неизменной.
В дальнейшем были введены другие функции
кислотности. В тех случаях, когда применяется в качестве индикатора
незаряженная кислота и соответствующее ей основание имеет отрицательный заряд, функцию
кислотности обозначают Н(-).
Метод Гамметта чрезвычайно прост и не связан с
измерением потенциалов, не имеет осложнений в связи с возникновением
потенциалов на границе двух фаз. Поэтому он представляет значительный интерес и
нашел широкое применение.
Однако последние работы показали, что нет
оснований считать, что в действительности величина Н0 передает
кислотность неводных растворов. Предположение о том, что константа индикатора
не изменяется при переходе от растворителя к растворителю, очень сомнительно.
Предположение Гамметта о неизменности констант
кислотности индикаторов-оснований равносильно предположению, что константы
кислотности оснований выражены через абсолютные активности, отнесенные к
водному раствору как к стандарту.
Искомой величиной является абсолютная активность
ионов лиония аМН+ отнесенная к водному раствору протонов
(ионов гидроксония) как к стандарту. Константа кислотности основания через
абсолютные активности выразится так:
КАосн=аВ+(М)(aB/aBH+) (2.4.4)
Заменив в уравнении (2.4.4) величины aB и aBH+ выражениями a=c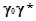 получим: получим:
KAосн=аH+(M)(cB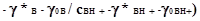 (2.4.5) (2.4.5)
где аH+(M) искомая абсолютная
активность сольватированного протона, отнесенная к его состоянию в
бесконечно разбавленном, водном растворе.
На основании уравнения (2.4.5) для КАосн
запишем выражение для рКА:
pKA=-lgKAосн=-lgaH+(M)( cB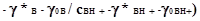 (2.4.6) (2.4.6)
Подставив это выражение в уравнение (2.4.3),
получим:
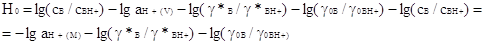 (2.4.7) (2.4.7)
Предположение Гамметта будет действительно
правильным, если окажется, что Н0 будет равно только логарифму
активности протонов в данном растворителе, отнесенному к единому стандартному
состоянию, т. е. к бесконечно разбавленному водному раствору. Но для этого
нужно, чтобы выражение 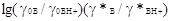 было равно нулю. было равно нулю.
Упростим нашу задачу: представим, что растворы
настолько разбавлены, что отношение концентрационных коэффициентов активности 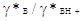 единице. Но и тогда в выражении остается
отношение единых коэффициентов активности единице. Но и тогда в выражении остается
отношение единых коэффициентов активности 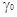 ;
они не зависят от концентрации. В этом случае выражение для Н0
примет вид: ;
они не зависят от концентрации. В этом случае выражение для Н0
примет вид:
Н0=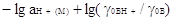 (2.4.8)
(2.4.8)
Из этого выражения следует, что Н0 не
равно логарифму активности протона, а отличается от него на величину логарифма
отношения коэффициентов активности 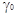 заряженной
и незаряженной форм индикатора т. е. зависит от того, какова энергия
взаимодействия с растворителем иона и нейтральной молекулы индикатора. При
стандартизации по отношению к бесконечно разбавленному водному раствору величины заряженной
и незаряженной форм индикатора т. е. зависит от того, какова энергия
взаимодействия с растворителем иона и нейтральной молекулы индикатора. При
стандартизации по отношению к бесконечно разбавленному водному раствору величины
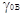 и и 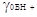 определяются работой
переноса ионов ВН+ и соответственно молекул В из среды М в
воду. Таким образом, предположение, что Н0 равно -lgaH+(M) будит справедливо
только в том случае, если влияние растворителя на катион основания и молекулу
основания индикатора одинаково. определяются работой
переноса ионов ВН+ и соответственно молекул В из среды М в
воду. Таким образом, предположение, что Н0 равно -lgaH+(M) будит справедливо
только в том случае, если влияние растворителя на катион основания и молекулу
основания индикатора одинаково.
Но все количественные данные, имеющиеся по этому
поводу, говорят о том, что это не так.
Шварценбах пытался сравнить ход изменения
величины Н0 и величины Н(-) в зависимости
от свойств растворителей. В соответствии со сказанным ранее величина Н(-)
будет выражена через единые коэффициенты активности так: 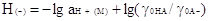 (2.4.9) (2.4.9)
По Шварценбаху, аналогия заключается в том, что
коэффициенты активности 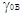 и и 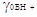 ,так же как и коэффициенты
активности ,так же как и коэффициенты
активности 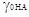 и и 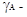 представляют коэффициенты
активности веществ, отличающихся только одним зарядом. представляют коэффициенты
активности веществ, отличающихся только одним зарядом.
Предположение Шварценбаха сводится к тому, что
отношение коэффициентов 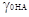 / / 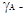 равно отношению равно отношению 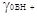 / /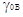
Оказалось, что это далеко не так. Исследование этих
функции кислотности в 0,002 н. раствора НС1 в смесях спирта с водой показало
для функции Н0 иную зависимость от содержания спирта, чем для
функции Н(-). Следовательно, Н(-) не передает истинной
кислотности раствора. Появление заряда на молекуле осложнит в результате
присоединения протона вызывает также резкое изменение энергии взаимодействия
незаряженной молекулы индикатора и ее иона с растворителем. Все это говорит о
том, что нельзя приравнивать изменение H0 к изменению кислотности.
Задача может быть решена, если будут известны 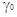 для
В и ВН+, только тогда Н0 можно исправить и найти
истинную величину -lg аН+(М). для
В и ВН+, только тогда Н0 можно исправить и найти
истинную величину -lg аН+(М).
Таким образом, ни Н0, ни Н(-)
не оценивают правильно единую кислотность растворов.
Очень существенным недостатком метода Гамметта
является также необходимость использования нескольких индикаторов при определении
кислотности. Согласно теории индикаторов, заметить изменение окраски, по
которой судят об изменении Н0, можно только тогда, когда будет
присутствовать не меньше 10% одной формы индикатора в присутствии 90% другой;
можно заметить окраску вещества ВН+, когда оно будет составлять
более 10% от вещества В, и наоборот. С помощью одного индикатора можно
определить изменение кислотности только в пределах 2 единиц рН и Н0.
В воде шкала рН=14; следовательно, нужно иметь
семь индикатором для оценки кислотности.
Рассмотрим, насколько метод Гаммета пригоден для
определения кислотности в пределах одного неводного растворителя.
Нельзя принимать, как это делает Гамметт, что в
неводных растворах соотношение между константами индикаторов остается таким же,
как и в воде. Как известно, растворитель оказывает дифференцирующее действие.
Оно сводится к тому, что относительная сила кислот или оснований изменяется при
переходе от одного растворителя к другому.
Разность в pК двух индикаторов
основания В1 и В2 определится выражением:
pKA1-pKA2=-lg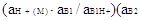 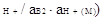   (2.4.10) (2.4.10)
Введем концентрационные активности а* и
коэффициенты активности 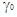 тогда
получим: тогда
получим:
pKA1-pKA2=-lg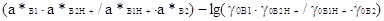 (2.4.11) (2.4.11)
Из уравнения (26) следует, что разность рK определяется не только
соотношением активностей а*, но и соотношением коэффициентов активности 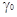 . Нет никаких оснований
утверждать, что . Нет никаких оснований
утверждать, что
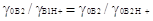 (2.4.12) (2.4.12)
и, следовательно, соотношение рКА не остается
неизменным.
Это обстоятельство затрудняет использование
метода Гамметта и в пределах одного растворителя. Необходима экспериментальная
проверка pK индикаторов в каждом растворителе.
Есть и третий недостаток метода Гамметта,
заключающийся в том, что иногда окраска индикатора изменяется не в связи с
изменением соотношения между разными формами индикаторов ВН+ и В, а
в связи с тем, что окраска одной из форм индикатора изменяется под влиянием
растворителя. Однако главный недостаток метода Гамметта состоит в том, что
влияние растворителей па заряженную и незаряженную формы индикатора не
одинаково, в связи с чем Н0 не передает истинной кислотности
неводных растворов.
Для оценки кислотности кроме функций Н0 и
Н(-) предложены функция Н(+), основанная на
зависимости положения равновесия реакции ВН2+ = В+
+ Н+ от кислотности, а также функция кислотности I0 , основанная на зависимости
положения равновесия реакции ROH + H+ =R+ + H2O (R+ - ион карбония, ROH-арилкарбинол) от кислотности.
Каждая функция кислотности определяется значением
соответствующих величин рК и отношением концентраций кислотной и основной
форм индикатора:
H0=pKBH++lg(cB/cBH+) H(-)=pKBH+lg(cB-/cBH)
I0=pKR++lg(cROH/cR+)
H(+)=pKBH2++lg(cB+/cBH2+)
Соотношение между этими функциями кислотности и
величиной истинной единой кислотности рА = -lg aH+ определяется следующими
выражениями:
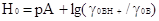 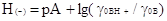
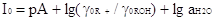
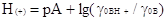
из
которых следует, что они не совпадают между собой и что ни один из них не
передает истинной кислотности.
2.5Метод нормального потенциала Плескова
Исследуя потенциалы щелочных металлов — лития,
натрия, калия , рубидия, цезия, - Плесков установил, что э. д. с. цепи Rb|Rb+||Cs+|Cs оказывается неизменной
во многих растворителях. На основании этого Плесков высказал предположение о
том, что потенциал цезиевого или рубидиевого электродов следует считать
неизменным в различных растворителях, т, е. считать, что э. д. с. Pt(H2)|H+||Cs+|Сs при переходе от одного
растворителя к другому изменяется не за счет цезиевого электрода, а только за
счет водородного электрода.
Однако неизменность разности потенциалов рубидия
и цезия не означает, что каждый из этих потенциалов не изменяется при переходе
от растворителя к растворителю - они изменяются, но в одинаковой степени.
Этот вывод был сделан на том основании , что изменение
потенциала цепи Hg(Cs) | CsCl | AgCl, Ag при переходе от воды к спирту близко к изменению потенциала цепи Pt(H2)|HCl|AgCl, Ag. В этих цепях анионы
одинаковы; следовательно, изменения потенциалов водородного и цезиевого
электродов (во всяком случае при переходе от воды к спиртам) близки между
собой. Поэтому не было оснований предполагать,, что изменение потенциала цепи
Pt(H2)|H+|Сs+| Cs во всех растворителях
обязано только водородному электроду; изменение потенциала обязано и
водородному и цезиевому электродам. Это говорит о том, что в общем нельзя
основывать оценку кислотности в неводных растворах на предположении Плескова.
Предположение Плескова оправдывается но отношению
к растворителям с высокой диэлектрической проницаемостью и резко отличной от
воды основностью (аммиак и муравьиная кислота), однако нельзя распространить
этот результат на другие растворители без экспериментальной проверки.
Строго, единая кислотность, которую мы обозначаем
рА, отнесенная к воде в качестве единого стандартного состояния, определяется
величиной отрицательного логарифма активности иона МН+:
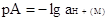 (2.5.1) (2.5.1)
где 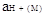 абсолютная
активность иона МН+ ,отнесенная к активности протона в разбавленном
водном растворе в качестве единого стандартного состояния. абсолютная
активность иона МН+ ,отнесенная к активности протона в разбавленном
водном растворе в качестве единого стандартного состояния.
Такая оценка кислотности является
термодинамически строго обоснованной. Единая активность ионов лиония,
отнесенная к воде в качестве стандартного состояния, может быть выражена так:
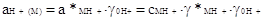 (2.5.2) (2.5.2)
Подставляя эту величину в уравнение (2.5.1),
получим:
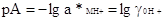 (2.5.3) (2.5.3)
в котором активность а* отнесена к бесконечно
разбавленному раствору ионов в неводной среде, а коэффициент 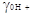  отнесен
к воде в качестве стандартного состояния. отнесен
к воде в качестве стандартного состояния.
Величина —lg а*МН+
называется рНр. Она может быть измерена для любого неводного
раствора против стандарта в том же самом неводном растворе. В определении этой
величины затруднений нет.
Следовательно
pA = pHр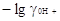 (2.5.4) (2.5.4)
Это однозначное определение величины рА.
2.6. Применение средних
коэффициентов активности 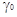 ионов
для оценки единой шкалы кислотности ионов
для оценки единой шкалы кислотности
Для оценки единой шкалы кислотности можно
воспользоваться средними коэффициентами активности ионов сильной соляной
кислоты.
Было установлено, что они могут быть определены
только для суммы электролитов в целом. Эти величины хорошо известны для ионов
ряда сильных кислот, особенно для HCl во многих растворителях. Например, для этилового
спирта 2lg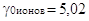 . Однако какая часть
величины 5,02 составляет lg . Однако какая часть
величины 5,02 составляет lg 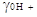 и какая часть lg и какая часть lg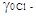 мы не знаем. В связи с этим
было предложено поступать так: принять, что средний коэффициент активности
ионов кислоты равен коэффициенту активности ионов лиония, т. е. предположить,
что: мы не знаем. В связи с этим
было предложено поступать так: принять, что средний коэффициент активности
ионов кислоты равен коэффициенту активности ионов лиония, т. е. предположить,
что:
lg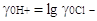 (2.6.1) (2.6.1)
Из этого предположения следует, что величина рА
определяется выражением
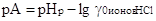 (2.6.2) (2.6.2)
Такой прием вносит определенную ошибку,
обусловленную различием в величинах 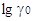 протонов
и анионов кислот, однако сравнение протонов
и анионов кислот, однако сравнение 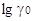 для
разных кислот показало, что эти величины близки между собой; например, для
разных кислот показало, что эти величины близки между собой; например,
и этиловом спирте 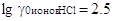 , ,
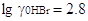 , , 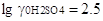 и т.д. Это же наблюдается
и для других растворителей. и т.д. Это же наблюдается
и для других растворителей.
Эксперименты показывают, что величины 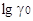 ионов кислот в спиртам лишь
несколько отличаются от величины: ионов кислот в спиртам лишь
несколько отличаются от величины: 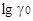 ионов
солей. Поэтому нельзя предполагать, что изменения энергии сольватации ионов
лиония резко отличается от изменения энергии сольватации остальных катионов. Во
всяком случае, величина ионов
солей. Поэтому нельзя предполагать, что изменения энергии сольватации ионов
лиония резко отличается от изменения энергии сольватации остальных катионов. Во
всяком случае, величина 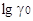 ионов
кислот является вполне однозначной и, вероятно, оценивает изменение кислотности
с большей надежностью, чем величины Н0, Н(-), рННас
и т.д. ионов
кислот является вполне однозначной и, вероятно, оценивает изменение кислотности
с большей надежностью, чем величины Н0, Н(-), рННас
и т.д.
2.7 Нахождение единой кислотности рА с помощью 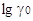 протонов протонов
Все перечисленные выше методы не позволяют
однозначно оценить кислотность неводных растворов в единой шкале. Вопрос об
этой шкале может быть решен только на основании данных о величинах химической
энергии сольватации протонов в различных растворителях. Эти данные получены на
основании подсчетов сумм и разностей химических энергий сольватации ионов в
неводных растворах из данных об электродвижущих силах цепей без переноса и с
переносом в неводных растворах. Путем экстраполяции величин суммарной энергии
сольватации ионов водорода и ионов галогенов (ионы галогеноводородных кислот)
и разностей энергий сольватации ионов водорода и ионов щелочных металлов была
определена энергия сольватации протона и других ионов в различных
растворителях.
При переходе от водного к неводному раствору
следует считаться с том, что протяженность шкалы различна для разных
растворителей. Для того чтобы оценить абсолютную кислотность, кроме
протяженности шкалы нужно знать, как смещено начало шкалы кислотности одного
растворителя но отношению к шкале кислотности воды.
Использование 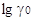 протонов
в различных растворителях в качестве единой меры изменения кислотности в разных
растворителях однозначно характеризует величину смещения шкал кислотности. протонов
в различных растворителях в качестве единой меры изменения кислотности в разных
растворителях однозначно характеризует величину смещения шкал кислотности.
Обозначим начало шкалы для воды через 0; шкала
для этилового спирта имеет протяженность 19,3; если 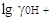 =
4,2, то очевидно, что шкала в этиловом спирте начинается в области —4,2 и
заканчивается при рА = 15,1. У метилового спирта =
4,2, то очевидно, что шкала в этиловом спирте начинается в области —4,2 и
заканчивается при рА = 15,1. У метилового спирта 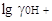 =
3,3, а вся шкала 16,9; шкала для него расположится от - 3,3 до +13,6; =
3,3, а вся шкала 16,9; шкала для него расположится от - 3,3 до +13,6; 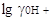 в муравьиной кислоте в муравьиной кислоте  = 8,6, вся шкала равна 6,1,
она расположена между -8,6 и -2,5. У аммиака протяженность шкалы 32,7; она
смещена по отношению к воде на 16,4 единицы, начало шкалы будет при рА = 16,4,
а конец при рА = 49,1. Из этих сопоставлений следует, что самый щелочной
раствор в муравьиной кислоте будет кислее самого кислого раствора в воде и
самый кислый раствор в аммиаке щелочнее самого щелочного раствора в воде, = 8,6, вся шкала равна 6,1,
она расположена между -8,6 и -2,5. У аммиака протяженность шкалы 32,7; она
смещена по отношению к воде на 16,4 единицы, начало шкалы будет при рА = 16,4,
а конец при рА = 49,1. Из этих сопоставлений следует, что самый щелочной
раствор в муравьиной кислоте будет кислее самого кислого раствора в воде и
самый кислый раствор в аммиаке щелочнее самого щелочного раствора в воде,
Относительное расположение шкалы рНр
позволяет оценить отношение между единой кислотностью растворов и величиной рНр.
Из рис. 2 следует, что раствор кислоты в спирте, в котором активность а*= (рНр=
0), кислее соответствующего йодного раствори на 4,2 единицы.

Рис. 2. Изменение рНр (1), рА (2), Н0
(3), и Н(-) (4) растворов HCl (I), и ацетатного буфера (II) в растворах этилового спирта в
воде.
Однако не нужно думать, что всякий раствор
кислоты в этиловом спирте будет кислее, чем в воде. В действительности рА
нормального раствора соляной кислоты в этиловом спирте не будет равна -4,2, так
как в нем величина 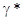 значительно
меньше величины значительно
меньше величины 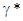 в воде. в воде.
Таким образом, в этиловом спирте, с одной
стороны, 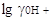 положителен, и это
приводит к уменьшению рА и увеличению кислотности. С другой стороны, lg положителен, и это
приводит к уменьшению рА и увеличению кислотности. С другой стороны, lg 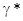 отрицательны и по
абсолютной величине больше, чем у воды, а это приводит к увеличению рНр
и к уменьшению кислотности. В 1 н. растворе HCl в этиловом спирте
величина отрицательны и по
абсолютной величине больше, чем у воды, а это приводит к увеличению рНр
и к уменьшению кислотности. В 1 н. растворе HCl в этиловом спирте
величина 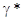 = 0,157. В результате этого
рА 1 н раствора HCl в этиловом спирте будет не -4,2, а значительно меньше (только
-3,3), но все же раствор в этиловом спирте значительно кислее, том в воде. = 0,157. В результате этого
рА 1 н раствора HCl в этиловом спирте будет не -4,2, а значительно меньше (только
-3,3), но все же раствор в этиловом спирте значительно кислее, том в воде.
Можно сказать, что в этиловом спирте каждый ион
лиония становится активнее, по число ионов лиония становится меньше.
Еще резче это будет проявляться в спиртовых растворах
уксусной кислоты: с одной стороны, кислотность ионов лиония С2Н5ОН2+
по сравнению с водой увеличивается на 4,2 единицы, но, с другой стороны,
константа диссоциации кислоты при переходе от воды к этиловому спирту
уменьшается на 5,6 порядка, и оба эффекта в значительной степени
компенсируются. Величина рА ацетатного буферного раствора только 5,5. Повышение
абсолютной кислотности будет особенно большим только в разбавленных растворах
сильных кислот, в которых 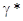 = 1. = 1.
Для иллюстрации на рис. 2 приведены данные для рН
и рА разбавленных растворов сильной соляной кислоты (0,002 н. НС1 + 0,008 н. NаCl) и буферных растворов,
состоящих из 0,02 н. НАс и 0,01 п. NaAc + 0,0005 н. NaCl в смесях этилового
спирта с водой.
Из рис.2 следует, что рНр разбавленных
растворов соляной кислоты практически не изменяются при переходе от воды к
спиртам. Наоборот, рА резко падают. В отличие от этого рНр
ацетатного буфера сильно возрастают в связи со значительным ослаблением силы
кислоты.. Величина рА этого буфера изменяется мало и не уменьшается, как в случае
растворов HCl, а несколько возрастает. Из рис, 2 следует также, что ни H0, ни Н(-) не
передают действительного хода зависимости единой кислотности с изменением
растворителя. Более того, Н(-) одного и того же раствора,
измеренная с помощью различных индикаторов [2,4-динитрофенол (Н(-))
и димедон (Н’(-))], расходятся. В этиловом
спирте они отличаются более чем на единицу рА. Еще большее расхождение между
рА, Н0 и Н(-) для раствором сильных кислот, где они
разнятся на 2—4 единицы.
3.Буферные растворы
Буферными называют растворы, рН которых
практически на изменяется от добавления к ним небольших количеств сильной
кислоты или щелочи, а также при разведении. Простейший буферный раствор – это
смесь слабой кислоты и соли, имеющей с этой кислотой общий анион (например,
смесь уксусной кислоты СН3СООН и ацетата натрия СН3СООNa), либо смесь слабого основания и
соли, имеющей с этим основанием общий катион (например, смесь гидроксида
аммония NH4OH с хлоридом аммония NH4Cl).
С точки зрения протонной
теории1 буферное действие растворов
обусловлено наличием кислотно-основного равновесия общего типа:
Воснование + Н+
Û ВН+сопряженная
кислота
НАкислота Û Н+ + А-сопряженное
основание
Сопряженные
кислотно-основные пары В /ВН+ и А- /НА называют буферными
системами.
3.1.Классификация
кислотно-основных буферных систем.
Буферные системы могут
быть четырех типов:
1.
Слабая кислота и
ее анион А- /НА:
·
Ацетатная
буферная система СН3СОО-/СН3СООН
в растворе СН3СООNa и
СН3СООН, область действия рН 3, 8 – 5, 8.
·
Водород-карбонатная
система НСО3-/Н2СО3
в растворе NaНСО3 и Н2СО3,
область её действия – рН 5, 4 – 7, 4.
2.
Слабое основание и
его катион В/ВН+:
·
аммиачная
буферная система NH3/NH4+ в растворе NH3 и NH4Cl,
область ее действия – рН 8, 2 – 10, 2.
3.
Анионы кислой и
средней соли или двух кислых солей:
·
карбонатная
буферная система СО32-
/НСО3- в растворе Na2CO3
и NaHCO3, область ее действия рН 9, 3 – 11, 3.
фосфатная буферная
система НРО42-/Н2РО4-
в растворе Nа2НРО4 и NаН2РО4, область
ее действия рН 6, 2 – 8, 2
Эти солевые буферные
системы можно отнести к 1-му типу, т. к. одна из солей этих буферных систем
выполняет функцию слабой кислоты. Так, в фосфатной буферной системе анион Н2РО4-
является слабой кислотой.
4. Ионы и молекулы
амфолитов. К ним относят аминокислотные и белковые буферные системы. Если
аминокислоты или белки находятся в изоэлектрическом состоянии (суммарный заряд
молекулы равен нулю), то растворы этих соединений не являются буферными. Они
начинают проявлять буферное действие, когда к ним добавляют некоторое
количество кислоты или щелочи. Тогда часть белка (аминокислоты) переходит из
ИЭС в форму “белок-кислота” или соответственно в форму “белок-основание”. При
этом образуется смесь двух форм белка: (R – макромолекулярный остаток белка)
а) слабая “белок-кислота”
+ соль этой слабой кислоты:
  СОО- СООН СОО- СООН
  R – СН + Н+ Û R – СН R – СН + Н+ Û R – СН
N+Н3 N+Н3
основание А-
сопряженная кислота НА
(соль белка-килоты)
(белок-кислота)
б) слабое
“белок-основание” + соль этого слабого основания:
  СОО- СОО- СОО- СОО-
  R – СН + ОН- Û R – СН + Н2О R – СН + ОН- Û R – СН + Н2О
N+Н3 NН2
кислота ВН+
сопряженное основание В
(соль белка-основания)
(белок-основание)
3.2.Определение pH стандартных буферных растворов
Используемые в качестве эталонов для измерений растворы
введены давно. Одним из первых таких стандартных растворов использовали «буфер»
Вейбеля, представлявший собой раствор 0.01 н. относительно HCl и 0.09 н.-KCl. Величину раН+
рассчитывали разными методами и приписывали различные значения. Кроме этого «буферного
раствора» в литературе рекомендуются наборы буферных растворов, имеющих
значения рН от 2 до 9, а также универсальные буферные растворы, оценка рН
которых производилась разными авторами по-разному.
Не было единой точки, зрения на методику
измерений. Таким образом, различия в полученных значениях инструментальных
величин рН для одного и того же исследуемого раствора доходили до 0,1, а иногда
и более единиц рН.
Однако рекомендованные буферные растворы обладали
большой величиной буферной емкости (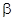 ),
количественно характеризуемой значением производной ),
количественно характеризуемой значением производной 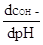 и
численно выражаемой количеством эквивалентов щелочи на 1 литр раствора,
необходимым для изменения рН и
численно выражаемой количеством эквивалентов щелочи на 1 литр раствора,
необходимым для изменения рН
раствора на единицу. Растворы использовались чаще
всего как среда с постоянной величиной рН, хорошо сохраняющая это постоянство,
но
само численное значение рН оценивалось
приближенно.
Начиная с 1950 г. появились работы Бейтса и
сотр., в которых поднят вопрос об оценке величины рН таких образцовых растворов
и о требованиях, которым должны отвечать сами растворы и вещества, из которых
их изготавливают. Эти требования сводятся к следующим:
1) для изготовления буферных образцовых растворов
вещества должны быть подобраны так, чтобы обеспечить определенное и не обязательно
максимальное значение буферной емкости раствора;
2) вещества должны быть такими, чтобы их легко
можно было получать в чистом виде (это обеспечивает возможность получения растворов
с хорошо воспроизводимыми значениями рН);
3) для определения величин paH+ буферных образцовых
растворов следует использовать измерение э. д. с. цепей без переноса типа :
Pt(H2) |буферный раствор + Cl-|AgCl, Ag (3.2.1)
и
расчетные методы для определения коэффициентов активности отдельного иона.
Метод расчета paH+ растворов, предложенный в
работах Бейтса и сотр., заключался в том, что по величинам э. д. с. цепи (3.2.1)
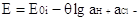 (3.2.2) (3.2.2)
измеренным в буферных растворах с различным
содержанием хлорид-ионов и стандартной э. д. с. этой цепи E0i можно найти величину
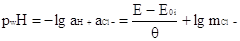 (3.2.3) (3.2.3)
где mCl- - концентрация хлорид - иона
в буферном растворе.
Экстраполируя величину pwH на нулевое содержание
хлорид - иона в растворе, можно
получить значение pwH0 , отвечающее величине 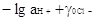 ,
где ,
где  - соответственно активность
иона водорода и коэффициент активности хлорид - иона при ионной силе буферного
раствора, не содержащего добавок хлорида. Из последнего по соотношению - соответственно активность
иона водорода и коэффициент активности хлорид - иона при ионной силе буферного
раствора, не содержащего добавок хлорида. Из последнего по соотношению
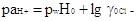 (3.2.4) (3.2.4)
рассчитывается искомая величина. Коэффициент
активности 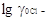 определяется
по уравнению Дебая определяется
по уравнению Дебая
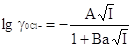 (3.2.5) (3.2.5)
где А, В - дебаевские коэффициенты; а -
расстояние наибольшего сближения ионов; I— ионная сила буферного
раствора.
Наибольшим недостатком предложенного метода
расчета 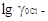 (количественное
соответствие между рассчитанной величиной и ее истинным значением) является
неопределенность параметра а. В связи с этим Бейтс ограничил применение
описанного метода буферными растворами с ионной силой не более 0,1. При этом
проверка показала, что вариации параметра а в физически разумных
границах 4-6 ангстрем изменяют величину раН+ на 0,01
единицы рН, что лежит в пределах погрешности самой определяемой
экспериментально величины рwН. (количественное
соответствие между рассчитанной величиной и ее истинным значением) является
неопределенность параметра а. В связи с этим Бейтс ограничил применение
описанного метода буферными растворами с ионной силой не более 0,1. При этом
проверка показала, что вариации параметра а в физически разумных
границах 4-6 ангстрем изменяют величину раН+ на 0,01
единицы рН, что лежит в пределах погрешности самой определяемой
экспериментально величины рwН.
Не имея возможности проверить определяемое значение раН+ буферного раствора
экспериментально, мы не можем согласиться с тем, что это значение нужно
рассматривать только как некую условно приписанную данному буферному раствору
величину.
Исследования Бейтса и сотр. положили начало практическим работам
по стандартизации величины раН+Шкала
кислотности водных растворов былареализована в виде набора буферных растворов,
охватывающих интервал рН от 1 до 12..
Вопрос о величинах диффузионных потенциалов неизбежных
спутников измерений э. д. с. в цепях с жидкостными границами не был решен.
Бейтс и сотр. исследовали остаточные диффузионные потенциалы, использовав
разработанные буферные растворы и выбрав один из них в качестве основного
стандарта. Результаты показали, что погрешности в определении раН+ «исследуемого» раствора
по отношению к выбранному за стандарт не превышали 0,01 единицы рН в том
случае, если значения раН+исследуемого
раствора отличались от стандартного в кислую сторону более, чем на 4 единицы, а
в щелочную - на 3 единицы рН. Для более щелочных растворов погрешности, связанные
с наличием остаточного диффузионного потенциала, превышали 0,01.
Из сказанного выше следует, что рассматриваемый метод стандартизации
измерений рН (оценка раН+ буферных
растворов) не является
безукоризненным.
Пользуясь этим приемом, нельзя создать образцовые буферные
растворы с ионной силой более 0,1, так как в этом случае уравнение Дебая не может быть применено для расчета коэффициента
активности хлорид - иона. Кроме того, некоторые исследователи не согласны с
тем, что предлагается несколько первичных стандартов, а не один, по отношению
к которому и производятся все измерения. Неопределенность параметра а в
уравнении Дебая также вызывает трудности.
Н. П. Комарь предложил иной метод так называемой
«юстировки» рН-метрических цепей, который, как казалось раньше, не только
решает проблему создания образцовых растворов с большой ионной силой, но и
открывает пути экспериментального определения коэффициентов активности
отдельного вида ионов.
Сущность метода заключается в следующем.
Электродвижущая сила цепи, обычно применяемой для измерения рН:
Электрод, обратимый к Н+|HCl(mHCl) |KCl|AgCl,Ag (3.2.6)
может быть представлена уравнением
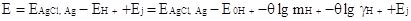 (3.2.7) (3.2.7)
Считая хлористый водород полностью
диссоциированным на ионы, можно вместо mH+ в уравнение (38)
подставить концентрацию mHCl.
Тогда мы приходим к уравнению
   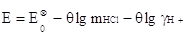 (3.2.8) (3.2.8)
где 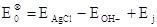 . И,
наконец, представляя . И,
наконец, представляя 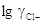 как функцию
ионной силы I в
виде полинома как функцию
ионной силы I в
виде полинома
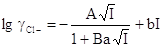 (3.2.9) (3.2.9)
можно прийти к выражению для э.д.с. цепи (37):
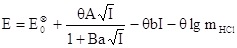 (3.2.10) (3.2.10)
Оставляя постоянной концентрацию хлористого водорода и меняя
ионную силу в растворе добавкой постороннего (фонового) электролита, например,
соли (КС1, KNО3, NaCl), можно получить ряд значений Е цепи
с определенным ионным фоном.
Это позволяет, используя способ наименьших квадратов, определить
постоянные уравнения (3.2.10) -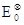 , а и b. , а и b.
Зная эти параметры, можно по уравнению (3.2.10) рассчитать 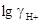 для любой ионной силы и
найти величину для любой ионной силы и
найти величину 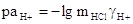 для всех исследуемых растворов. для всех исследуемых растворов.
Таким образом, любой из исследованных растворов с любой интересующей
нас ионной силой может быть использован для «юстировки» цепи (3.2.6) по этим растворам.
Достаточно один раз измерить э. д. с. цепи типа (3.2.6) (уже с другими электродами) в растворе с
рассчитанным ранее значением paH+ для вычисления Е0, и такую цепь можно использовать для
определения paH+ неизвестных растворов.
Преимуществом этого метода является то, что параметры а и
b в уравнении дебаевского типа
вычисляются по экспериментальным данным. При этом устраняется неопределенность
при нахождении а в уравнении Дебая по методу, описанному ранее.
Однако метод, предложенный Н. П. Комарем, не лишен некоторых
недостатков. Так, для определения из экспериментальных данных коэффициентов
активности отдельного вида ионов он сделал допущение, что диффузионный
потенциал Еj не зависит от
ионной силы раствора. Поэтому полученные коэффициенты активности не могут
рассматриваться как величины, найденные без каких - либо нетермодинамических допущений, т.е. нельзя
считать, что paH+ стандартного раствора не содержат
никаких погрешностей. Кроме того, при измерении рН исследуемых растворов не.
исключаются погрешности, связанные с наличием остаточных диффузионных
потенциалов, так как из двух измерений э. д. с. цепи (со стандартным раствором
для определения Е0 и с исследуемым) мы фактически используем
для расчета э. д. с. цепи, аналогичной цепи :
Pt(H2) |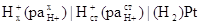
При этом остаточный диффузионный потенциал  , равный разности
диффузионных потенциалов Ej на границах исследуемый
раствор- раствор соединительного моста, соединительный раствор - стандартный
раствор, искажает инструментальную величину рН. , равный разности
диффузионных потенциалов Ej на границах исследуемый
раствор- раствор соединительного моста, соединительный раствор - стандартный
раствор, искажает инструментальную величину рН.
Таким образом, применение метода Н. П. Комаря
хотя и позволяет использовать в качестве стандартов растворы с известным раH+ с различными ионными
силами на различных ионных фонах, но не устраняет ошибок, связанных с
остаточным диффузионным потенциалом.
Кроме того, наборы таких растворов (с известным раH++ и ионными силами от
~0,01 до ~3,5 m имеют значения раH+, не сильно отличающиеся друг от друга (на 0,5 -
1,0 единиц) с абсолютными величинами - в кислой области около 2, в щелочной -
около 12. Значит, по величине раH+ они могут существенно отличаться от рН
исследуемого раствора, что, в свою очередь, увеличивает остаточный диффузионный
потенциал.
Оптимальным условием для определения рН
исследуемых растворов и снижения остаточного диффузионного потенциала до нуля
было бы равенство стандартного и исследуемого растворов, по раH+, ионной силе и
составу фонов. Однако в практике измерения рН такое невозможно.
Сопоставления результатов измерения рН некоторых
модельных растворов, проведенные этими методами, показали, что результаты
незначительно отличаются друг от друга, что и следовало ожидать, поскольку в
основу положено уравнение одного типа (Дебаевское), а погрешности за счет
диффузионных потенциалов различаются несущественно, и уточнения за счет
величины параметра а не выходят за пределы погрешности метода
(приблизительно 0,01 ед. рН).
ВЫВОД:
В работе были изучены методы определения
кислотности неводных растворов, стандартизация ее измерения. Рассмотрены методы
определения pH стандартных буферных растворов в соответствии с допустимыми
погрешностями.
СПИСОК ЛИТЕРАТУРЫ:
1.
Кислотность неводных растворов. В. В. Александров, 152 с. граф. 20 см., Харьков Вища школа
Изд-во при Харьк. ун-те 1981
2.
Измайлов Н.А., Электрохимия
растворов, 3 изд., испр., М., «Химия», 1976, 488 с.
3.
Бейтс Р. Определение pH: Теория и практика. Л.:
Химия, 1968, 398 с.
4.
Васильев В. П. Аналитическая химия. В 2 кн. Кн.
2. Физико-химические методы анализа: Учеб. для студ. вузов, обучающихся по
химико-технол. спец. - 2-е изд., перераб. и доп. - М.:Дрофа, 2002. - 384 с.,
ил. - с. 191.
5.
Кнорре Д. Г., Крылова Л. Ф., Музыкантов В. С.
Физическая химия: Учеб. пособие для вузов. - М.: Высш. школа, 1981. - 328 с.,
ил., с. 263-264.
|