Реферат: Конические сечения
Реферат: Конические сечения
Муниципальное
Образовательное Учреждение
Средняя
Общеобразовательная школа №4
Конические
сечения
Выполнил
Спиридонов
Антон
ученик 11
А класса
Проверил
Коробейникова
А. Т.
Тобольск –
2006 г.
ОГЛАВЛЕНИЕ.
Введение
Понятие конических сечений
Виды конических
сечений
Исследование
Построение конических
сечений
Аналитический подход
Применение
Приложение
Список литературы
Введение.
Цель: изучить конические
сечения.
Задачи: научиться различать
виды конических сечений, строить кинические сечения и применять аналитический
подход.
Конические сечения впервые предложил
использовать древнегреческий геометр Менехм, живший в IV веке до нашей эры, при
решении задачи об удвоении куба. Эту задачу связывают со следующей легендой.
Однажды на
острове Делосе вспыхнула эпидемия чумы. Жители острова обратились к оракулу,
который сказал, что для прекращения эпидемии надо увеличить вдвое золотой
жертвенник, который имел форму куба и находился в храме Аполлона в Афинах.
Островитяне изготовили новый жертвенник, ребра которого были вдвое больше ребер
прежнего. Однако чума не прекратилась. Разгневанные жители услышали от оракула,
что неверно поняли его предписание — удвоить было надо не ребра куба, а его
объём, то есть увеличить ребра куба в 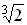 раз. В терминах геометрической
алгебры, которой пользовались греческие математики, задача означала: по данному
отрезку а найти такие отрезки х и y такие, что а : х = х : y = y : 2a. Тогда
длина отрезка х будет равна раз. В терминах геометрической
алгебры, которой пользовались греческие математики, задача означала: по данному
отрезку а найти такие отрезки х и y такие, что а : х = х : y = y : 2a. Тогда
длина отрезка х будет равна 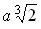 . .
Приведенную
пропорцию можно рассматривать как систему уравнений:
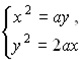
Но x2=ay
и y2=2ax — это уравнения парабол. Поэтому для решения задачи следует
отыскать точки их пересечения. Если же учесть, что из системы можно получить и
уравнение гиперболы xy=2a2, то эту же задачу возможно решить
нахождением точек пересечения параболы с гиперболой.
Для получения
конических сечений Менехм пересекал конус - остроугольный, прямоугольный или
тупоугольный — плоскостью, перпендикулярной одной из образующих. Для
остроугольного конуса сечение плоскостью, перпендикулярной к его образующей,
имеет форму эллипса. Тупоугольный конус при этом дает гиперболу, а прямоугольный
– параболу.
Отсюда
произошли и названия кривых, которые были введены Аполлонием Пергским, жившим в
III веке до нашей эры: эллипс (έλλείψίς
), что означает изъян, недостаток (угла конуса до прямого); гипербола (ύπέρβωλη)
— преувеличение, перевес (угла конуса над прямым); парабола (παραβολη)
— приближение, равенство (угла конуса прямому углу). Позже греки заметили, что
все три кривые можно получить на одном конусе, изменяя наклон секущей
плоскости. При этом следует брать конус, состоящий из двух полостей и мыслить,
что они простираются в бесконечность (Рис. 1).
Если провести
сечение кругового конуса, перпендикулярное его оси, а потом поворачивать
секущую плоскость, оставляя одну точку её пересечения с конусом неподвижной, то
увидим, как окружность будет сначала вытягиваться, превратившись в эллипс.
Затем вторая вершина эллипса уйдет в бесконечность, и вместо эллипса получится
парабола, а потом плоскость пресечет и вторую полость конуса и получится
гипербола.
Понятие
конических сечений.
Конические сечения - это плоские кривые, которые получаются пересечением прямого
кругового конуса плоскостью, не проходящей через его вершину. С точки зрения
аналитической геометрии коническое сечение представляет собой геометрическое
место точек, удовлетворяющих уравнению второго порядка. За исключением
вырожденных случаев, рассматриваемых в последнем разделе, коническими сечениями
являются эллипсы, гиперболы или параболы (Рис. 2).
При вращении
прямоугольного треугольника около одного из катетов, гипотенуза с ее
продолжениями описывает коническую поверхность, называемую поверхностью прямого
кругового конуса, которая может быть рассматриваема как непрерывный ряд прямых,
проходящих через вершину и называемых образующими, причем все образующие опираются
на одну и ту же окружность, называемую производящей. Каждая из образующих
представляет собой гипотенузу вращающегося треугольника (в известном его
положении), продолженную в обе стороны до бесконечности. Таким образом, каждая
образующая простирается по обе стороны от вершины, вследствие чего и
поверхность имеет две полости: они сходятся в одну точку в общей вершине. Если
такую поверхность пересечь плоскостью, то в сечении получится кривая, которая и
называется коническим сечением. Она может быть трех типов:
1) если
плоскость пересекает коническую поверхность по всем образующим, то рассекается
только одна полость и в сечении получается замкнутая кривая, называемая эллипсом;
2) если
секущая плоскость пересекает обе полости, то получается кривая, имеющая две
ветви и называемая гиперболой;
3) если
секущая плоскость параллельна одной из образующих, то получается парабола.
Если секущая
плоскость параллельна производящей окружности, то получается окружность,
которая может быть рассматриваема как частный случай эллипса. Секущая плоскость
может пересекать коническую поверхность только в одной вершине, тогда в сечении
получается точка, как частный случай эллипса.
Если
плоскостью, проходящей через вершину, пересекаются обе полости, то в сечении
получается пара пересекающихся прямых, рассматриваемая как частный случай гиперболы.
Если вершина бесконечно удалена, то коническая
поверхность обращается в цилиндрическую, и сечение ее плоскостью, параллельной
образующим, дает пару параллельных прямых как частный случай параболы. Конические
сечения выражаются уравнениями 2-го порядка, общий вид которых
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
и называются кривыми 2-го
порядка.
Виды конических
сечений.
Конические
сечения могут быть трёх типов:
1) секущая плоскость пересекает все
образующие конуса в точках одной его полости; линия пересечения есть замкнутая
овальная кривая — эллипс; окружность как частный случай эллипса получается,
когда секущая плоскость перпендикулярна оси конуса.
2) Секущая плоскость параллельна
одной из касательных плоскостей конуса; в сечении получается незамкнутая,
уходящая в бесконечность кривая — парабола, целиком лежащая на одной полости.
3) Секущая плоскость пересекает обе
полости конуса; линия пересечения — гипербола — состоит из двух одинаковых
незамкнутых, простирающихся в бесконечность частей (ветвей гиперболы), лежащих
на обеих полостях конуса.
Исследование.
В тех
случаях, когда конические сечение имеет центр симметрии (центр), т. е. является
эллипсом или гиперболой, его уравнение может быть приведено (путём перенесения
начала координат в центр) к виду:
a11x2+2a12xy
+ a22y2 = a33.
Дальнейшие
исследования таких (называемых центральными) конические сечения показывают, что
их уравнения могут быть приведены к ещё более простому виду:
Ах2
+ Ву2 = С,
если за
направления осей координат выбрать главные направления — направления главных
осей (осей симметрии) конических сечений. Если А и В имеют одинаковые знаки
(совпадающие со знаком С), то уравнение определяет эллипс; если А и В разного
знака, то — гиперболу.
Уравнение
параболы привести к виду (Ах2 + Ву2 = С) нельзя. При
надлежащем выборе осей координат (одна ось координат — единственная ось
симметрии параболы, другая — перпендикулярная к ней прямая, проходящая через
вершину параболы) её уравнение можно привести к виду:
y2
= 2рх.
ПОСТРОЕНИЕ КОНИЧЕСКИХ
СЕЧЕНИЙ.
Изучая
конические сечения как пересечения плоскостей и конусов, древнегреческие
математики рассматривали их и как траектории точек на плоскости. Было
установлено, что эллипс можно определить как геометрическое место точек, сумма
расстояний от которых до двух заданных точек постоянна; параболу – как
геометрическое место точек, равноудаленных от заданной точки и заданной прямой;
гиперболу – как геометрическое место точек, разность расстояний от которых до
двух заданных точек постоянна.
Эти
определения конических сечений как плоских кривых подсказывают и способ их
построения с помощью натянутой нити.
Эллипс.
Если концы нити заданной длины закреплены в точках F1 и F2
(рис. 3), то кривая, описываемая острием карандаша, скользящим по туго
натянутой нити, имеет форму эллипса. Точки F1 и F2
называются фокусами эллипса, а отрезки V1V2
и v1v2
между точками пересечения эллипса с осями координат – большой и малыми
осями. Если точки F1
и F2
совпадают, то эллипс превращается в окружность (Рис. 3).
Гипербола. При построении гиперболы точка P,
острие карандаша, фиксируется на нити, которая свободно скользит по шпенькам,
установленным в точках F1 и F2, как
показано на рисунке 4, а, расстояния подобраны так, что отрезок PF2
превосходит по длине отрезок PF1 на фиксированную величину,
меньшую расстояния F1F2. При этом один конец нити
проходит под шпеньком F1, и оба конца нити проходят поверх шпенька F2.
(Острие карандаша не должно скользить по нити, поэтому его нужно закрепить,
сделав на нити маленькую петлю и продев в нее острие.) Одну ветвь гиперболы (PV1Q) мы
вычерчиваем, следя за тем, чтобы нить оставалась все время натянутой, и,
потягивая оба конца нити вниз за точку F2, а когда точка P
окажется ниже отрезка F1F2, придерживая нить за оба
конца и осторожно отпуская ее. Вторую ветвь гиперболы мы вычерчиваем,
предварительно поменяв шпеньки F1 и F2 (Рис.
4).
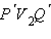
Ветви
гиперболы приближаются к двум прямым, которые пересекаются между ветвями. Эти
прямые, называемые асимптотами
гиперболы, строятся, как показано на рисунке 4,б.
Угловые
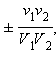
коэффициенты
этих прямых равны где – отрезок биссектрисы угла между асимптотами,
перпендикулярной отрезку F2F1; отрезок
v1v2
называется сопряженной осью гиперболы, а отрезок V1V2
– ее поперечной осью. Таким образом, асимптоты являются диагоналями
прямоугольника со сторонами, проходящими через четыре точки v1, v2, V1, V2
параллельно осям. Чтобы построить этот прямоугольник, необходимо указать
местоположение точек v1 и v2. Они
находятся на одинаковом расстоянии, равном
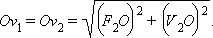
от точки
пересечения осей O.
Эта формула предполагает построение прямоугольного треугольника с катетами Ov1
и V2O и
гипотенузой F2O.
Если
асимптоты гиперболы взаимно перпендикулярны, то гипербола называется равнобочной. Две гиперболы, имеющие
общие асимптоты, но с переставленными поперечной и сопряженной осями,
называются взаимно
сопряженными.
Парабола.
Фокусы эллипса и гиперболы были известны еще Аполлонию, но фокус параболы, по-видимому, впервые
установил Папп (вторая пол. III в.), определивший эту кривую как
геометрическое место точек, равноудаленных от заданной точки (фокуса) и
заданной прямой, которая называется директрисой. Построение параболы с
помощью натянутой нити, основанное на определении Паппа, было предложено
Исидором Милетским (VI в.) (Рис. 5).
Расположим
линейку так, чтобы ее край совпал с директрисой, и приложим к этому краю катет AC
чертежного треугольника ABC. Закрепим один конец нити длиной AB в
вершине B
треугольника, а другой – в фокусе параболы F. Натянув острием
карандаша нить, прижмем острие в переменной точке P к свободному катету AB
чертежного треугольника. По мере того, как треугольник будет перемещаться вдоль
линейки, точка P
будет описывать дугу параболы с фокусом F и директрисой, так как общая длина
нити равна AB,
отрезок нити прилегает к свободному катету треугольника, и поэтому оставшийся
отрезок нити PF
должен быть равен оставшейся части катета AB, то есть PA.
Точка пересечения V
параболы с осью называется вершиной параболы, прямая, проходящая
через F и V, – осью параболы.
Если через фокус провести прямую, перпендикулярную оси, то отрезок этой прямой,
отсекаемый параболой, называется фокальным параметром.
Для эллипса и гиперболы фокальный параметр определяется аналогично.
АНАЛИТИЧЕСКИЙ ПОДХОД
Алгебраическая
классификация. В
алгебраических терминах конические сечения можно определить как плоские кривые,
координаты которых в декартовой системе координат удовлетворяют уравнению
второй степени. Иначе говоря, уравнение всех конических сечений можно записать
в общем, виде как
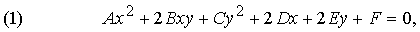
где не все
коэффициенты A, B и C равны нулю. С помощью параллельного переноса и поворота
осей уравнение (1) можно привести к виду
ax2 + by2 + c = 0
или
px2 + qy = 0.
Первое
уравнение получается из уравнения (1) при B2 > AC, второе – при B2
= AC. Конические сечения, уравнения которых приводятся к первому виду,
называются центральными. Конические сечения, заданные уравнениями второго вида
с q > 0, называются нецентральными. В рамках этих двух категорий
существуют девять различных типов конических сечений в зависимости от знаков
коэффициентов.
1) Если
коэффициенты a, b и c имеют один и тот же знак, то не существует вещественных
точек, координаты которых удовлетворяли бы уравнению. Такое коническое сечение
называется мнимым эллипсом (или мнимой окружностью, если a = b).
2) Если a и b
имеют один знак, а c – противоположный, то коническое сечение – эллипс; при a =
b – окружность.
3) Если a и b
имеют разные знаки, то коническое сечение – гипербола .
4) Если a и b
имеют разные знаки и c = 0, то коническое сечение состоит из двух
пересекающихся прямых.
5) Если a и b
имеют один знак и c = 0, то существует только одна действительная точка на
кривой, удовлетворяющая уравнению, и коническое сечение – две мнимые
пересекающиеся прямые. В этом случае также говорят о стянутом в точку эллипсе
или, если a = b, стянутой в точку окружности.
6) Если либо a,
либо b равно нулю, а остальные коэффициенты имеют разные знаки, то коническое
сечение состоит из двух параллельных прямых.
7) Если либо a,
либо b равно нулю, а остальные коэффициенты имеют один знак, то не существует
ни одной действительной точки, удовлетворяющей уравнению. В этом случае
говорят, что коническое сечение состоит из двух мнимых параллельных прямых.
8) Если c =
0, и либо a, либо b также равно нулю, то коническое сечение состоит из двух
действительных совпадающих прямых. (Уравнение не определяет никакого
конического сечения при a = b = 0, поскольку в этом случае исходное уравнение
(1) не второй степени.)
9) Уравнения
второго типа определяют параболы, если p и q отличны от нуля. Если p > 0, а q
= 0, мы получаем кривую из п. 8. Если же p = 0, то уравнение не определяет
никакого конического сечения, поскольку исходное уравнение (1) не второй
степени.
Применение
Конические сечения часто
встречаются в природе и технике. Например, орбиты планет, обращающихся вокруг
Солнца, имеют форму эллипсов. Окружность представляет собой частный случай
эллипса, у которого большая ось равна малой. Параболическое зеркало обладает
тем свойством, что все падающие лучи, параллельные его оси, сходятся в одной
точке (фокусе). Это используется в большинстве телескопов-рефлекторов, где
применяются параболические зеркала, а также в антеннах радаров и специальных
микрофонах с параболическими отражателями. От источника света, помещенного в фокусе
параболического отражателя, исходит пучок параллельных лучей. Поэтому в мощных
прожекторах и автомобильных фарах используются параболические зеркала.
Гипербола является графиком многих важных физических соотношений, например,
закона Бойля (связывающего давление и объем идеального газа) и закона Ома,
задающего электрический ток как функцию сопротивления при постоянном напряжении
Приложение
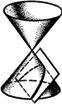 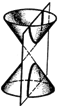 
л
Рис. 1
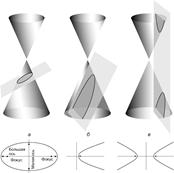
Рис. 2
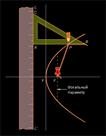 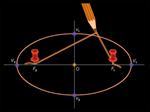
Рис. 3
Рис. 4
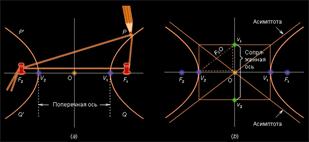
Рис. 5
Список литературы.
1. Алексеев. Теорема Абеля в задачах и решениях.
2001
2. Базылев В. Т., Дуничев К. И.,
Иваницкая В. П.. Учебное пособие для студентов 1 курса физико-математических
факультетов педагогических институтах. Москва «просвещение» 1974
3. Верещагин Н.К., А.Шень. Лекции по математической логике и
теории алгоритмов. 1999
4. Гельфанд И.М.. Лекции по линейной
алгебре. 1998.
5. Гладкий А.В.. Введение в современную логику. 2001
6. М.Э.Казарян. Курс дифференциальной геометрии
(2001-2002).
7. Прасолов В.В.. Геометрия Лобачевского 2004
8. Прасолов В.В.. Задачи по планиметрии 2001
9. Шейнман О.К.. Основы теории представлений. 2004
|