Курсовая работа: Замкнутые сети с многорежимными стратегиями обслуживания
Курсовая работа: Замкнутые сети с многорежимными стратегиями обслуживания
Курсовая работа
"Замкнутые сети с многорежимными стратегиями обслуживания"
Введение
Важными задачами для развития современного общества являются сбор,
обработка, хранение и распространение информации. Передача информации
представляет собой основу для решения этих задач и потому требует тщательного
изучения. Адекватное описание процесса передачи информации с помощью
математических моделей может быть осуществлено в рамках теории массового обслуживания.
При этом для многих реальных систем такой процесс моделируется посредством
сетей массового обслуживания. Например, к указанному результату приводит
математическое моделирование мультипрограммных вычислительных систем и анализ
их производительности, проектирование и анализ сетей передачи данных и сетей
ЭВМ.
В начале XX века датский ученый А.К. Эрланг, работавший на
копенгагенской телефонной станции, поставил и решил ряд новых математическтх
задач, позволивших оценивать характеристики телефонных и телеграфных линий
связи. Это способствовало возникновению нового направления в теории
вероятностей – теории массового обслуживания. На начальной стадии своего
развития теория массового обслуживания имела дело с системами массового
обслуживания, которые описываются потоками однородных заявок, поступающих в
систему, процедурами обслуживания с помощью одного или нескольких каналов,
процедурами формирования очередей и способами организации процесса ожидания
заявок. Строгое научное описание случайных процессов в теории массового
обслуживания и их всестороннее исследование впервые было осуществлено А.Я. Хинчиным.
Он исследовал одноканальную систему с ожиданием, простейшим входным потоком и
рекуррентным обслуживанием, установив для нее так называемый основной закон
стационарной очереди: стационарное распределение числа заявок в системе
совпадает с их стационарным распределением в случайные моменты ухода заявок из
системы. Большой вклад в развитие теории массового обслуживания внесли Ю.К. Беляев,
А.А. Боровков, Б.В. Гнеденко, Н. Джейсуолл, Дж.Р. Джексон, Ф.П. Келли,
Дж. Кендалл, Дж.Ф.С. Кингмэн, Л. Клейнрок, Г.П. Климов, И.Н. Коваленко,
С. Пальм, Ф. Поллачек, Ю.В. Прохоров, Дж. Риордан, Т. Саати,
В.Л. Смит и др.
В 1957 г. Дж.Р. Джексон впервые ввел в рассмотрение понятие
открытой сети массового обслуживания ([99]), а в 1967 г. Гордон и Ньюэлл
ввели аналогичное понятие замкнутой сети ([91]). В отличие от системы массового
обслуживания сеть представляет собой более сложное образование, состоящее из
систем массового обслуживания, называемых узлами сети, которые взаимодействуют
между собой с помощью некоторого вероятностного механизма. В открытых сетях
заявки могут поступать извне, а также уходить из сети. В замкнутых сетях
сохраняется постоянное число заявок, которые с помощью случайной маршрутизации
могут перемещаться между узлами сети; при этом поступление заявок в сеть и уход
заявок из сети невозможны.
Результаты Джексона и Гордона-Ньюэлла не использовались до тех
пор, пока в 1971 г. Ф.Р. Мур [115] не обнаружил, что замкнутые сети
адекватно описывают вычислительные системы со многими ресурсами. С этого
момента теория сетей обслуживания стала быстро развиваться благодаря задачам,
связанным с математическим моделированием мультипрограммных вычислительных
систем и анализом их производительности, с проектированием и анализом сетей
передачи данных и сетей ЭВМ. Дополнительный толчок к дальнейшему развитию
теории дала разработка и использование в повсеместной практике различных
глобальных и локальных сетей таких, например, как EZERNET, INTERNET и т.д.
Значительный вклад в развитие теории сетей внесли Г.П. Башарин, А.А. Боровков,
Э. Геленбе, Дж. Джексон, В.А. Ивницкий, Ф.П. Келли, Д. Кениг,
Л. Клейнрок, Ю.В. Малинковский, М. Миязава, Б. Меламед, Р. Мюнтц,
С.Е.М. Перс, П.К. Поллетт, А.Н. Рыбко, Р. Серфозо, Ю.М. Сухов,
П. Тейлор, А.Л. Толмачев, Д. Тоусли, П. Уиттли, Дж. Уолрэнд,
Г.И. Фалин, В. Хендерсон, Х. Чао, К. Ченди, Р. Шассбергер
и многие другие.
Состояние сети массового обслуживания обычно характеризуется
вектором, координаты которого описывают состояния отдельных узлов сети. В силу
многомерности случайного процесса состояний и статистической зависимости между
координатами исследование сетей массового обслуживания на порядок сложнее, чем
исследование систем массового обслуживания. Даже в случае экспоненциальных
сетей, когда случайный процесс состояний является марковским, его эргодическое
стационарное распределение удовлетворяет настолько сложной системе уравнений,
что решить ее удается в основном только тогда, когда решение имеет форму
произведеня. Множители в этом произведении зависят только от свойств
индивидуальных узлов. В имеющейся литературе по стационарному распределению
экспоненциальных сетей практически не рассматриваются сети с ненадежными или
частично ненадежными приборами. В считанных работах рассмотрены только очень
частные вырожденные случаи и то для сетей, состоящих из двух узлов. В то же
время в практических ситуациях оборудование может частично или полностью
выходить из строя. Например, при работе на персональном компьютере очень часто
нарушаются функциональные связи между некоторыми файлами, программами или
другими элементами, хотя компьютер продолжает работать. Налицо частичная потеря
работоспособности, а значит, уменьшение интенсивности обслуживания.
Поэтому в диссертационной работе предпринята попытка построения
моделей, адекватно описывающих такую ситуацию. Рассмотрены экспоненциальные
сети с многорежимными стратегиями обслуживания, в которых обслуживающие
устройства в узлах частично ненадежны и в различных режимах функционирования
работают с разными интенсивностями. Для таких сетей находится инвариантная
вероятностная мера в мультипликативной форме.
1. Сети с переключением режимов при
определенном количестве заявок в узле
Рассматриваются замкнутые сети массового обслуживания с
экспоненциальным обслуживанием в узлах и марковской маршрутизацией.
Однолинейные узлы могут работать в нескольких режимах, время переключения с
одного режима на другой имеет показательное распределение. Переключение
происходит только на соседние режимы и с определенными ограничениями на
переключения в отдельных режимах. Устанавливается достаточное условие
мультипликативности стационарного распределения состояний сети.
Пусть 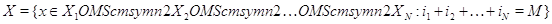 , где , где 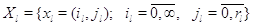 . На фазовом пространстве . На фазовом пространстве 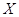 задан многомерный
марковский процесс задан многомерный
марковский процесс 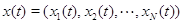 , где , где 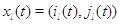 , своими инфинитезимальными
интенсивностями перехода , своими инфинитезимальными
интенсивностями перехода
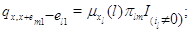
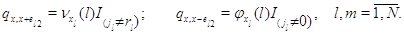
Интенсивности перехода из состояния 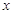 во
все состояния, отличные от вышеперечисленных, предполагаются равными нулю.
Здесь во
все состояния, отличные от вышеперечисленных, предполагаются равными нулю.
Здесь 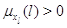 при при 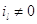 и и 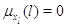 при при 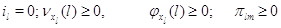 и и 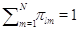 . .
Марковский процесс 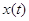 описывает
замкнутую сеть, в которой циркулирует описывает
замкнутую сеть, в которой циркулирует 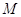 заявок.
В заявок.
В 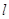 -м узле находится
единственный экспоненциальный прибор с интенсивностью обслуживания -м узле находится
единственный экспоненциальный прибор с интенсивностью обслуживания 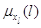 , зависящей от состояния
узла. Заявка, обслуженная в , зависящей от состояния
узла. Заявка, обслуженная в 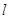 -м узле,
переходит с вероятностью -м узле,
переходит с вероятностью 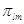 в в 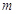 -й узел. Как и в случае
открытых сетей компонента -й узел. Как и в случае
открытых сетей компонента 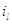 выражает
число заявок в выражает
число заявок в 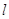 -м узле, а
компонента -м узле, а
компонента 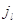 – номер режима работы
прибора. Прибор – номер режима работы
прибора. Прибор 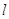 -го узла может
работать в -го узла может
работать в 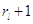 режимах режимах 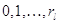 с показательно
распределенным временем пребывания в них; с показательно
распределенным временем пребывания в них; 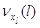 –
интенсивность увеличения номера режима на единицу, –
интенсивность увеличения номера режима на единицу, 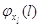 –
интенсивность уменьшения номера режима на единицу. –
интенсивность уменьшения номера режима на единицу.
Глобальные уравнения равновесия для стационарных вероятностей
этого марковского процесса имеют следующую форму:
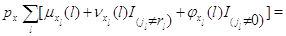
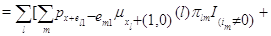
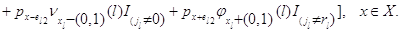
Рассмотрим общий случай, когда для каждого узла  существует натуральное
число существует натуральное
число 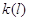 и конечное множество
индексов и конечное множество
индексов 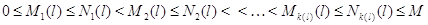 такое, что такое, что 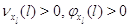 для всех для всех 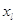 , у которых , у которых 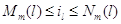 для некоторого для некоторого 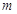 и и 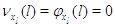 для всех для всех 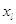 иного вида. иного вида.
Будем предполагать, что матрица 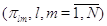 неприводима.
Тогда уравнение трафика неприводима.
Тогда уравнение трафика
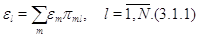
имеет единственное с точностью до постоянного множителя положительное
решение 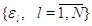 . Рассмотрим марковский
процесс . Рассмотрим марковский
процесс 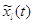 на фазовом пространстве на фазовом пространстве 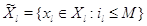 , заданный
инфинитезимальными интенсивностями , заданный
инфинитезимальными интенсивностями
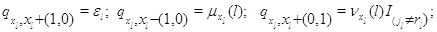
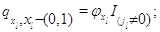
для всех иных состояний 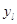 считаем,
что считаем,
что 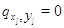 . Процесс . Процесс 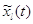 описывает изолированный
узел в фиктивной окружающей среде, в которой на узел посылается стационарный
пуассоновский поток с параметром описывает изолированный
узел в фиктивной окружающей среде, в которой на узел посылается стационарный
пуассоновский поток с параметром 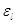 , где , где 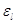 – любое решение уравнения
трафика (3.1.1). При этом узел предполагается имеющим ограниченную емкость – любое решение уравнения
трафика (3.1.1). При этом узел предполагается имеющим ограниченную емкость 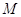 . Это значит, что когда в
нем находится . Это значит, что когда в
нем находится 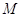 заявок и
поступает заявка, то она теряется. Уравнения равновесия для стационарных
вероятностей марковского процесса, описывающего такой узел, имеют следующий
вид: заявок и
поступает заявка, то она теряется. Уравнения равновесия для стационарных
вероятностей марковского процесса, описывающего такой узел, имеют следующий
вид:
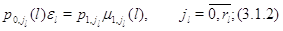
для 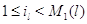
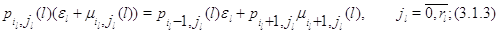
для 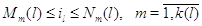
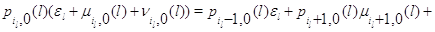
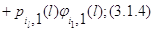
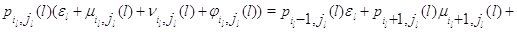
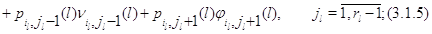
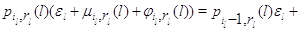
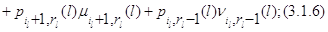
для 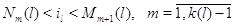 и для и для 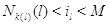
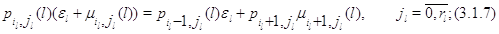
для 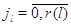
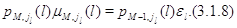
Мы свяжем стационарное распределение 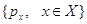 процесса процесса
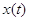 со стационарными
распределениями со стационарными
распределениями 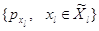 процессов процессов 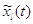 и будем интересоваться
достаточными условиями выполнения равенства и будем интересоваться
достаточными условиями выполнения равенства
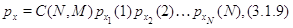
где 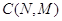 – нормирующая
постоянная, зависящая от числа узлов в сети и от числа циркулирующих в ней
заявок. – нормирующая
постоянная, зависящая от числа узлов в сети и от числа циркулирующих в ней
заявок.
В отличие от открытой сети, здесь удобнее пользоваться введенной в
[36,37,42] концепцией ограниченной квазиобратимости. Как там показано, для
замкнутых сетей ограниченная квазиобратимость дает более широкие достаточные
условия для выполнения (3.1.9), чем квазиобратимость.
Лемма 1.1 [46, C.325]. Если
для изолированного узла в фиктивной окружающей среде входящий поток является
простейшим, то обратимость и ограниченная квазиобратимость эквивалентны.
Д о к а з а т.е. л ь с т в о. Для изолированного узла условие
ограниченной 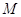 -квазиобратимости из
[36,37,42] принимает вид -квазиобратимости из
[36,37,42] принимает вид
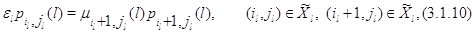
а условие обратимости – форму
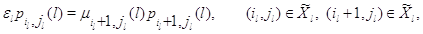
и для 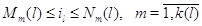
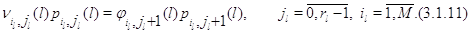
Достаточно показать, что при выполнении (3.1.2) – (3.1.8) из
(3.1.10) следует (3.1.11). Пусть 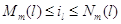 при
некотором фиксированном при
некотором фиксированном 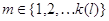 .
Докажем, что тогда для всех .
Докажем, что тогда для всех 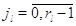 выполняется
(3.1.11). При выполняется
(3.1.11). При 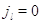 соотношение
(3.1.11) следует из (3.1.4) и соотношения (3.1.10) для состояний соотношение
(3.1.11) следует из (3.1.4) и соотношения (3.1.10) для состояний 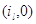 и и 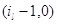 . Предположим, что (3.1.11)
выполняется для некоторого . Предположим, что (3.1.11)
выполняется для некоторого 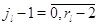 , т.е. , т.е.
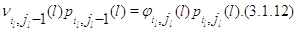
Тогда из (3.1.5) с учетом (3.1.12) и (3.1.10) для состояний 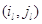 и и 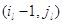 вытекает (3.1.11). Итак,
(3.1.11) доказано с помощью индукции по вытекает (3.1.11). Итак,
(3.1.11) доказано с помощью индукции по 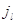 .
Лемма доказана. .
Лемма доказана.
Лемма 1.2 [46, C.325]. Для
ограниченной 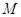 -квазиобратимости
изолированного -квазиобратимости
изолированного 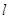 -го узла
необходимо и достаточно выполнения условий -го узла
необходимо и достаточно выполнения условий
а) для 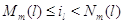 при
некотором при
некотором 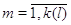
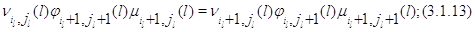
б) для всех 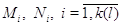
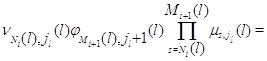
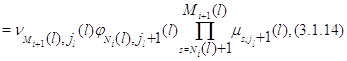
где при 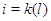 не определенная
ранее величина не определенная
ранее величина 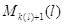 должна быть
заменена на должна быть
заменена на 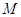 . Марковский процесс . Марковский процесс 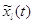 эргодичен, а его финальное
стационарное распределение с точностью до постоянной нормировки эргодичен, а его финальное
стационарное распределение с точностью до постоянной нормировки 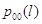 определяется соотношениями определяется соотношениями
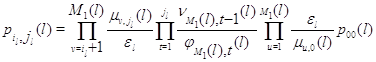
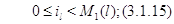
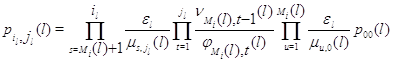
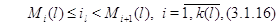
где при 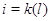 последнее
неравенство надо заменить на последнее
неравенство надо заменить на 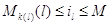 . .
Д о к а з а т.е. л ь с т в о. Рассмотрим случайное блуждание по
точкам с целочисленными координатами прямоугольника 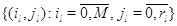 ,
задаваемое уравнениями (3.1.2) – (3.1.8). Равенство (3.1.13) есть циклическое
условие Колмогорова (2.2.18) для четырехзвенных путей, проходящих через вершины
элементарного квадрата ,
задаваемое уравнениями (3.1.2) – (3.1.8). Равенство (3.1.13) есть циклическое
условие Колмогорова (2.2.18) для четырехзвенных путей, проходящих через вершины
элементарного квадрата 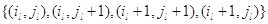 и
идущих из и
идущих из 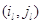 в в 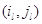 по и против часовой
стрелки. Равенство (3.1.14) есть условие Колмогорова для по и против часовой
стрелки. Равенство (3.1.14) есть условие Колмогорова для 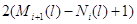 -звенных путей, проходящих
через вершины прямоугольника -звенных путей, проходящих
через вершины прямоугольника 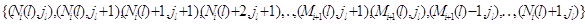 и
ведущих из и
ведущих из 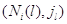 в в 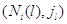 по и против часовой
стрелки. Это доказывает необходимость условий (3.1.13) и (3.1.14) для
обратимости, а значит (по лемме 3.1) ограниченной по и против часовой
стрелки. Это доказывает необходимость условий (3.1.13) и (3.1.14) для
обратимости, а значит (по лемме 3.1) ограниченной 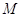 -квазиобратимости
изолированного узла в фиктивной окружающей среде. Предположим, что (3.1.13),
(3.1.14) выполнены. Любой замкнутый путь из -квазиобратимости
изолированного узла в фиктивной окружающей среде. Предположим, что (3.1.13),
(3.1.14) выполнены. Любой замкнутый путь из 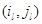 в в
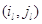 без самопересечений либо
а) представляет собой некоторую однозвенную замкнутую дугу, либо б) проходит по
границе некоторой фигуры, составленной из конечного числа примыкающих друг к
другу элементарных квадратов и определенных выше без самопересечений либо
а) представляет собой некоторую однозвенную замкнутую дугу, либо б) проходит по
границе некоторой фигуры, составленной из конечного числа примыкающих друг к
другу элементарных квадратов и определенных выше 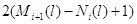 -
звенных прямоугольников. Для случая а) циклическое условие (2.2.18) выполняется
автоматически. В случае б) перемножим равенства (3.1.13) для всех элементарных
квадратов и равенства (3.1.14) для всех прямоугольников, из которых состоит
упомянутая фигура. При этом интенсивности перехода для тех направленных дуг,
которые не принадлежат границе фигуры, войдут множителями как в левую, так и в
правую части. После сокращения на них получится циклическое условие (2.2.18)
для путей, идущих по границе фигуры по и против часовой стрелки. Достаточность
условий (3.1.13) и (3.1.14) доказана. -
звенных прямоугольников. Для случая а) циклическое условие (2.2.18) выполняется
автоматически. В случае б) перемножим равенства (3.1.13) для всех элементарных
квадратов и равенства (3.1.14) для всех прямоугольников, из которых состоит
упомянутая фигура. При этом интенсивности перехода для тех направленных дуг,
которые не принадлежат границе фигуры, войдут множителями как в левую, так и в
правую части. После сокращения на них получится циклическое условие (2.2.18)
для путей, идущих по границе фигуры по и против часовой стрелки. Достаточность
условий (3.1.13) и (3.1.14) доказана.
Докажем, что стационарное распределение изолированного узла в
фиктивной окружающей среде имеет форму (3.1.15), (3.1.16). Полагая в (3.1.11) 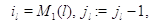 получим: получим:
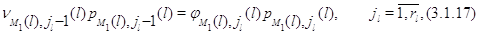
откуда получаем
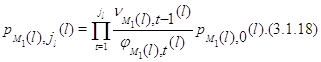
Из (3.1.10) для 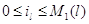 находим,
что находим,
что
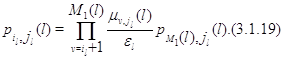
Для таких же 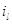 из
(3.1.10) также следует, что из
(3.1.10) также следует, что
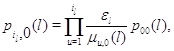
в частности,
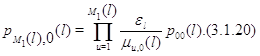
Подставляя (3.1.20) в (3.1.18), а затем подставляя полученное
равенство в (3.1.19), будем иметь для 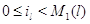
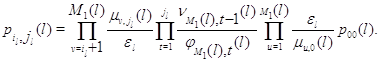
Тем самым доказано (3.1.15).
Для 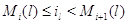 из (3.1.10)
следует, что из (3.1.10)
следует, что
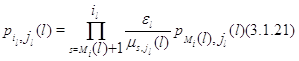
Полагая в (3.1.11) 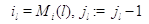 ,
получим: ,
получим:
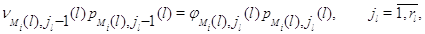
откуда
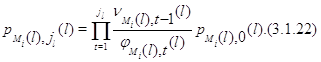
Далее, из (3.1.10)
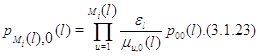
Подставляя (3.1.23) в (3.1.22), а затем полученное равенство в
(3.1.21), для 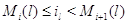 будем иметь будем иметь
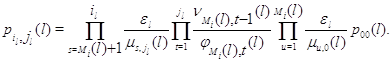
Таким образом, (3.1.16) доказано для 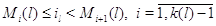
Для 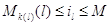 из (3.1.10)
следует, что из (3.1.10)
следует, что
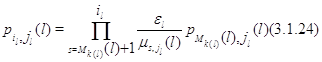
Полагая в (3.1.11) 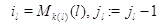 ,
получим: ,
получим:
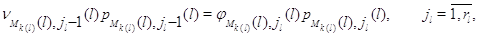
откуда
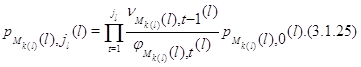
Далее, из (3.1.10)
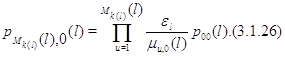
Подставляя (3.1.26) в (3.1.25), а затем полученное равенство в
(3.1.24), получим (3.1.16), которое таким образом доказано и для 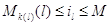 . .
Так как 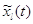 – неприводимый
процесс Маркова с конечным числом состояний и непрерывным временем, то по
эргодической теореме Маркова [5] он является эргодическим. Лемма 3.2 полностью
доказана. – неприводимый
процесс Маркова с конечным числом состояний и непрерывным временем, то по
эргодической теореме Маркова [5] он является эргодическим. Лемма 3.2 полностью
доказана.
Основной результат 3.1 заключается в следующем.
Теорема 1.1. [46, C.326], [53, C.159–160], [56, C.325–326] Марковский процесс 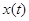 эргодичен.
Для того, чтобы его стационарное распределение представлялось в форме
произведения (3.1.9), достаточно, чтобы во всех узлах сети выполнялись условия
(3.1.13), (3.1.14). При этом множители в (3.1.9) имеют форму (3.1.15), (3.1.16),
в которых полагается, что эргодичен.
Для того, чтобы его стационарное распределение представлялось в форме
произведения (3.1.9), достаточно, чтобы во всех узлах сети выполнялись условия
(3.1.13), (3.1.14). При этом множители в (3.1.9) имеют форму (3.1.15), (3.1.16),
в которых полагается, что 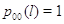 , а
постоянная , а
постоянная 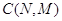 имеет вид: имеет вид:
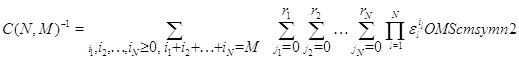
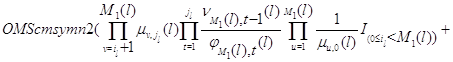
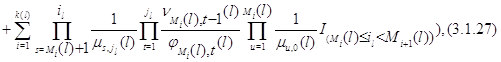
где 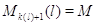 . .
Д о к а з а т.е. л ь с т в о. Так как марковский процесс с
непрерывным временем и конечным числом состояний является неприводимым, то он
эргодичен по эргодической теореме Маркова [5]. В [42] для замкнутых сетей с «заявкосохраняющими»
 узлами установлено, что
для мультипликативности стационарного распределения достаточно, чтобы
нетерминальные узлы являлись ограниченно узлами установлено, что
для мультипликативности стационарного распределения достаточно, чтобы
нетерминальные узлы являлись ограниченно 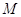 -квазиобратимыми.
Поэтому, с учетом условия ограниченной -квазиобратимыми.
Поэтому, с учетом условия ограниченной 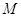 -квазиобратимости
для изолированного узла, которое в силу леммы 3.2 для узла с номером -квазиобратимости
для изолированного узла, которое в силу леммы 3.2 для узла с номером 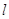 принимает форму (3.1.13),
(3.1.14), имеет место первое утверждение теоремы. принимает форму (3.1.13),
(3.1.14), имеет место первое утверждение теоремы.
Наконец, поскольку сумма всех стационарных вероятностей должна
быть равна единице, то подставляя в равенство
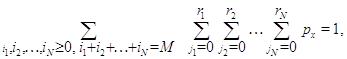
вместо 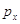 произведение
(3.1.9) и учитывая (3.1.15), (3.1.16), после очевидных преобразований получим произведение
(3.1.9) и учитывая (3.1.15), (3.1.16), после очевидных преобразований получим
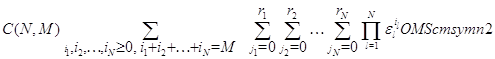
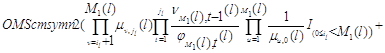
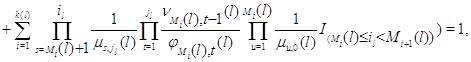
откуда вытекает (3.1.27). Теорема доказана.
Замечание 3.1. Если условия (3.1.13),
(3.1.14) выполнены во всех узлах, то получается следующий алгоритм для
нахождения стационарных вероятностей:
1. Решается система линейных уравнений (3.1.1). В качестве
используемого в дальнейшем набора 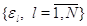 берется
любой набор со строго положительными координатами. берется
любой набор со строго положительными координатами.
2. Проверяется выполнение условий (3.1.13), (3.1.14).
3. По формуле (3.1.27) определяется постоянная нормировки 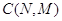 . .
4. Определяются 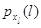 с
помощью соотношений (3.1.15), (3.1.16). с
помощью соотношений (3.1.15), (3.1.16).
5. Находится стационарное распределение состояний сети 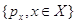 с помощью формулы (3.1.9). с помощью формулы (3.1.9).
Отметим также, что если в сети есть узлы, в которых условия
(3.1.13), (3.1.14) не выполняются, то алгоритм существенно усложнится, так как
в этих узлах нельзя применить (3.1.15), (3.1.16). Поэтому для таких узлов
необходимо добавить процедуру численного решения системы уравнений (3.1.2) –
(3.1.8). При этом изменится также выражение для подсчета нормирующей постоянной
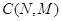 . Известно, что наиболее
трудоемким этапом при вычислении стационарного распределения для замкнутых
сетей является этап подсчета нормирующей постоянной. Существуют различные
численные процедуры, разработанные для ее вычисления, например, анализ средних
значений [10], или алгоритм, рекуррентный по времени [4,10]. . Известно, что наиболее
трудоемким этапом при вычислении стационарного распределения для замкнутых
сетей является этап подсчета нормирующей постоянной. Существуют различные
численные процедуры, разработанные для ее вычисления, например, анализ средних
значений [10], или алгоритм, рекуррентный по времени [4,10].
2. Примеры замкнутых сетей с
переключением режимов
В 3.1 рассматривалась весьма общая модель замкнутой сети с
многорежимными стратегиями. Здесь мы рассмотрим несколько полезных для
различных приложений частных случаев этой модели. Во всех рассматриваемых ниже
примерах предполагается, что для 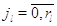 выполняется выполняется
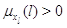 при при 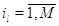 и и 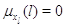 при при 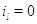 . .
Случай 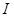 .
Пусть для всех .
Пусть для всех 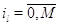 выполняется выполняется 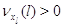 для для 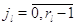 и и 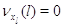 для для 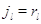 , а также , а также 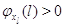 для для 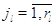 и и 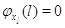 для для 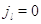 . Это соответствует тому,
что в модели из 3.1 полагается . Это соответствует тому,
что в модели из 3.1 полагается 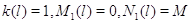 .
Теорема 3.1 принимает следующий вид. .
Теорема 3.1 принимает следующий вид.
Следствие 2.1. Марковский процесс 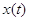 эргодичен. Для того, чтобы
его стационарное распределение представлялось в мультипликативной форме
(3.1.9), достаточно, чтобы во всех узлах сети выполнялись условия эргодичен. Для того, чтобы
его стационарное распределение представлялось в мультипликативной форме
(3.1.9), достаточно, чтобы во всех узлах сети выполнялись условия
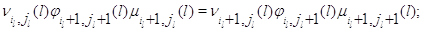
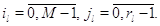
Множители в (3.1.9) имеют форму
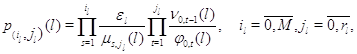
а постоянная нормировки имеет вид
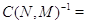
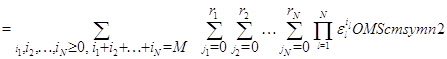
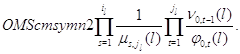
Случай 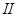 .
Во многих практических ситуациях переход с одного режима работы на другие
невозможен, когда в узле нет заявок. Поэтому пусть для всех .
Во многих практических ситуациях переход с одного режима работы на другие
невозможен, когда в узле нет заявок. Поэтому пусть для всех 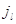 выполняется выполняется 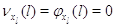 при при 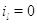 . Пусть также для всех . Пусть также для всех 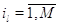 выполняется выполняется 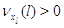 для для 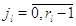 и и 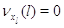 для для 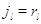 , а также , а также 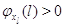 для для 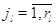 и и 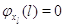 для для 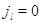 . Это соответствует тому,
что в модели из 3.1 полагается . Это соответствует тому,
что в модели из 3.1 полагается 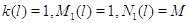 . .
Следствие 2.2. Марковский процесс 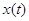 эргодичен. Для того, чтобы
его стационарное распределение представлялось в мультипликативной форме
(3.1.9), достаточно, чтобы во всех узлах сети выполнялись условия эргодичен. Для того, чтобы
его стационарное распределение представлялось в мультипликативной форме
(3.1.9), достаточно, чтобы во всех узлах сети выполнялись условия
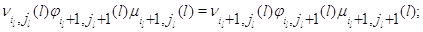
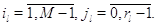
Множители в (3.1.9) имеют форму
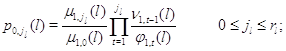
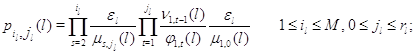
а постоянная нормировки имеет вид
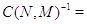
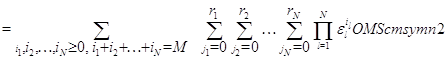
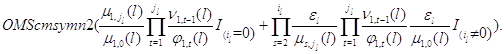
Случай 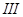 .
Предположим, что когда все .
Предположим, что когда все 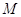 заявок
скапливаются в одном узле, прибор не может переходить с одного режима работы на
другие: заявок
скапливаются в одном узле, прибор не может переходить с одного режима работы на
другие: 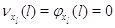 при при 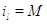 . Пусть также для всех . Пусть также для всех  выполняется выполняется 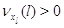 для для 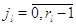 и и 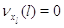 для для 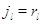 , а также , а также 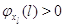 для для 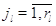 и и 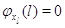 для для 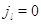 . Это соответствует тому,
что в модели из 3.1 полагается . Это соответствует тому,
что в модели из 3.1 полагается 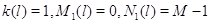 . .
Следствие 2.3. Марковский процесс 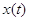 эргодичен. Для того, чтобы
его стационарное распределение представлялось в мультипликативной форме
(3.1.9), достаточно, чтобы во всех узлах сети выполнялись условия эргодичен. Для того, чтобы
его стационарное распределение представлялось в мультипликативной форме
(3.1.9), достаточно, чтобы во всех узлах сети выполнялись условия
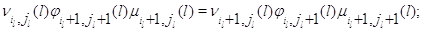
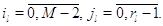
Множители в (3.1.9) имеют форму
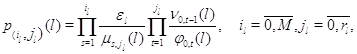
а постоянная нормировки имеет вид
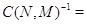
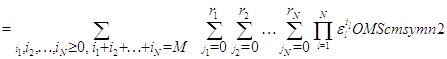
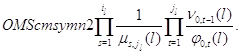
Случай 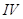 .
Когда в узле нет заявок или все заявки скапливаются в нем, переход с одного
режима работы на другие невозможен: .
Когда в узле нет заявок или все заявки скапливаются в нем, переход с одного
режима работы на другие невозможен: 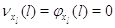 при при 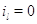 или или 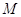 . Пусть также для всех . Пусть также для всех 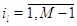 выполняется выполняется 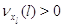 для для 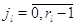 и и 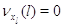 для для 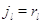 , а также , а также 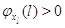 для для 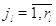 и и 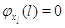 для для 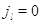 . Это соответствует тому,
что в модели из 3.1 полагается . Это соответствует тому,
что в модели из 3.1 полагается 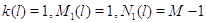 . .
Следствие 2.4. Марковский процесс 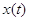 эргодичен. Для того, чтобы
его стационарное распределение представлялось в мультипликативной форме
(3.1.9), достаточно, чтобы во всех узлах сети выполнялись условия эргодичен. Для того, чтобы
его стационарное распределение представлялось в мультипликативной форме
(3.1.9), достаточно, чтобы во всех узлах сети выполнялись условия
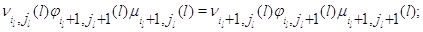
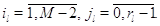
Множители в (3.1.9) имеют форму
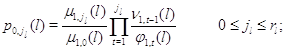
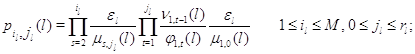
а постоянная нормировки имеет вид
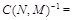 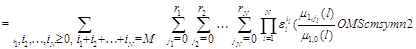
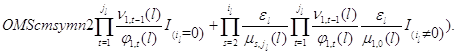
В следующих двух случаях стационарное распределение всегда имеет
форму произведения, поскольку марковский процесс, описывающий изолированный
узел в фиктивной окружающей среде, обратим. Поэтому не надо накладывать никаких
ограничений типа (3.1.13), (3.1.14).
Случай 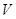 .
Прибор может переключаться с одного режима работы на другие только тогда, когда
в узле нет заявок: для .
Прибор может переключаться с одного режима работы на другие только тогда, когда
в узле нет заявок: для 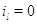 выполняется выполняется 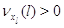 при при 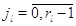 и и 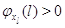 при при 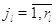 . Кроме того для всех . Кроме того для всех 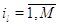 выполняется выполняется 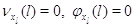 . Это соответствует тому,
что в модели из 3.1 полагается . Это соответствует тому,
что в модели из 3.1 полагается 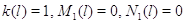 . .
Следствие 2.5. Марковский процесс 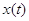 эргодичен, а его
стационарное распределение представляется в мультипликативной форме (3.1.9),
множители в которой имеют форму эргодичен, а его
стационарное распределение представляется в мультипликативной форме (3.1.9),
множители в которой имеют форму
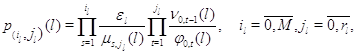
а постоянная нормировки имеет вид
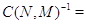 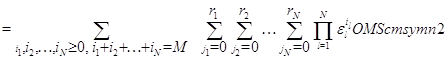
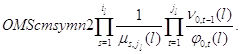
Случай 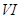 .
Переход с одного режима работы прибора на другие возможен только тогда, когда
все заявки скапливаются в узле: для .
Переход с одного режима работы прибора на другие возможен только тогда, когда
все заявки скапливаются в узле: для 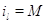 выполняется выполняется
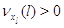 при при 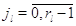 и и 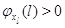 при при 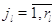 . Кроме того для всех . Кроме того для всех 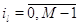 выполняется выполняется 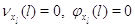 . Это соответствует тому,
что в модели из 3.1 полагается . Это соответствует тому,
что в модели из 3.1 полагается 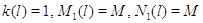 . .
Следствие 2.6. Марковский процесс 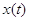 эргодичен, а его
стационарное распределение представляется в мультипликативной форме (3.1.9),
множители в которой имеют форму эргодичен, а его
стационарное распределение представляется в мультипликативной форме (3.1.9),
множители в которой имеют форму
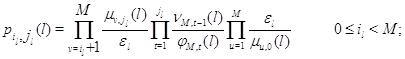
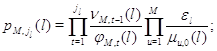
Можно выписать решения для других интересных с практической точки
зрения случаев. Например, можно рассмотреть случай, когда переключение с одного
режима работы на другой может производиться только при определенном
фиксированном числе заявок в  -ом узле -ом узле  , где , где 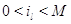 . В этом случае марковский
процесс . В этом случае марковский
процесс 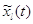 обратим без всяких
дополнительных предположений типа (3.1.13), (3.1.14). обратим без всяких
дополнительных предположений типа (3.1.13), (3.1.14).
Заключение
В работе рассмотрена задача установления достаточных условий,
которые надо наложить на изолированные узлы замкнутой сети массового
обслуживания с многорежимными стратегиями обслуживания, чтобы стационарное
распределение состояний сети имело мультипликативную форму с множителями,
зависящими от состояний отдельных узлов. При этом изолированные узлы помещаются
в фиктивную окружающую среду, характеризующуюся поступлением в них
пуассоновских потоков заявок. Такие достаточные условия мультипликативности
стационарного распределения состояний замкнутой сети в стационарном режиме ее
работы установлены как для случая, когда интенсивности перехода в соседние
режимы работы строго положительны при любых числах заявок в узлах, так и для
случая, когда при определенных числах заявок в узлах они строго положительны, а
при других числах все они равны нулю.
Доказана эргодичность марковского процесса, описывающего состояния
сети. При выполнении установленных достаточных условий мультипликативности в
аналитической форме найдены множители в мультипликативном представлении
стационарного распределения и нормирующая постоянная. Построен алгоритм для
расчета стационарных вероятностей состояний сети.
Литература
1. Кениг Д., Рыков В.В., Шмидт Ф. Стационарные системы
массового обслуживания с зависимостями // Итоги науки и техники. – М.,
1981. – Т.18. – С. 95–186. – (Сер. Теория вероятностей. Матем. статистика.
Теор. кибернетика / ВИНИТИ).
2. Клейнрок Л. Коммуникационные сети. – М.: Наука, 1970. – 255 с.
3. Клейнрок Л. Вычислительные системы с очередями. – М.: Мир,
1979. – 600 с.
4. Климов Г.П. Стохастические системы обслуживания. – М.:
Наука, 1966. – 243 с.
5. Ковалев Е.А. Сети с ненадежными каналами и резервом //
Математические методы исследования сетей связи и сетей ЭВМ. Тезисы докладов VI
Белорусской школы-семинара по ТМО. – Минск, 1990. – С. 70–71.
6. Ковалев Е.А., Чикунова Н.А. Стационарное
распределение двухузловой замкнутой ненадежной сети с делящимся резервом //
Материалы международной конференции «Современные математические методы
исследования телекоммуникационных сетей». – Минск, 1999. – С. 85–89.
7. Кофман А., Крюон Р. Массовое обслуживание. Теория и
приложения. – М.: Мир, 1965. – 302 с.
8. Крыленко А.В. Сети массового обслуживания с
несколькими типами заявок, немедленным обслуживанием и обходами узлов заявками //
Проблемы передачи информации. – 1997. – Т. 33, Вып. 3. – С. 91–101.
9. Крыленко А.В. Малинковский Ю.В. Сети
массового обслуживания с мгновенно обслуживаемыми заявками II. Модели с
несколькими тинами заявок // Автоматика и телемеханика. – 1998. – №2. – С. 62–71.
10. Крыленко А.В., Малинковский Ю.В. Замкнутые сети
массового обслуживания с обходами узлов и несколькими классами заявок //
Becni Акад. навук Беларусi. Сер. ф1з.-мат. навук. – 1998. – №2. – С.
11. Крыленко А.В. Инвариантность стационарного
распределения замкнутых сетей массового обслуживания с обходами узлов,
неэкспоненциальным обслуживанием и несколькими типами заявок // Becni
Акад. навук
12. Крыленко A.В., Малинковский Ю.В. Сети обслуживания с
обходами и несколькими классами заявок // Исследование систем и сетей
массового обслуживания: Тез. докл. 12‑й Бел. зимней школы-семинара по
ТМО, Гр., 1996 г. / Бел. гос. унив. – 1996. – С. 48–49.
13. Крыленко А.В., Малинковский Ю.В. Замкнутые сети
массового обслуживания с обходами узлов и несколькими классами заявок //
VII Белорусская математ. конф. Тез. докл. науч. конф., Минск, 18–22 нояб. 1996 г.
/ Бел. матем. общ-во, Бел. гос. унив., Ин‑т матем-ки Академии наук
Беларуси. – 1996.
14. Крыленко А.В. Инвариантность сетей массового
ообслуживанием и обходами узлов заявками // Математические методы исследования
телекоммуникационных сетей: Материалы 13‑й Бел. зимней школ. (науч. конф.
BWWQT‑97), Минск, 3 – 1997 г. / Бел. гос. унив. – 1997. – С. 50–52.
15. Малинковский Ю.В. Критерий точечной независимости
состояний узлов в открытой стационарной марковской сети обслуживания с одним
классом заявок // Теория вероятностей и ее применения. – 1990. – Т.35, №4.
– С. 779–784.
16. Малинковский Ю.В. Мультипликативность стационарного
распределения открытых сетей обслуживания со стандартными узлами и однотипными
заявками // Проблемы передачи информации. – 1999. – Том 35, Вып.1. – С. 96–110.
17. Малинковский Ю.В. Мультипликативность стационарного
распределения состояний для одного класса сетей массового обслуживания //
Автоматика и телемеханика. – 1988. – №2. – С. 108–118.
|