Контрольная работа: Математические основы теории систем
Контрольная работа: Математические основы теории систем
Задача 1. Элементы теории графов
Связный ориентированный граф G (Х, Г) задан множеством вершин X={x1,
x2, …, xn} и отображением Гxi=,
i =1, 2,…, n. Здесь i - текущий номер вершины, n-
количество вершин графа. Значение индексов n,
k и l возьмем
из табл.1 в соответствии с номером варианта. Индексы k
и l формируют значения индексов a, b , g… переменной x в отображении Гxi
= {xa ,
xb , xg,…}.
Если значения индексов a,
b, g… переменной x не соответствуют ни одному из номеров вершин графа, то
эта переменная не учитывается во множестве Гxi.
Выполнить следующие действия:
а) определить исходный граф и
ассоциированный с ним неориентированный граф графическим, матричным и
аналитическим способами;
б) установить центры и
периферийные вершины графов, найти радиусы и диаметры графов;
в) выделить в ориентированном
графе два подграфа. Найти объединение, пересечение и разность подграфов;
г) описать систему уравнений,
соответствующую сигнальному графу, считая, что передача между вершинами xi и xj
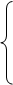 i*j при i ³ j; i*j при i ³ j;
Kij =
1/ (p+1)
при i<j
.
Найти передачу между вершинами x1 и xn,
используя правило Мезона. Построить структуру кибернетической системы,
определяемой топологией графа;
Таблица 1
|
№
варианта
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| N |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
6 |
6 |
6 |
6 |
6 |
6 |
| K |
2 |
3 |
4 |
1 |
1 |
1 |
3 |
5 |
2 |
4 |
2 |
3 |
4 |
5 |
6 |
| L |
1 |
1 |
1 |
2 |
3 |
4 |
2 |
1 |
3 |
3 |
1 |
1 |
1 |
1 |
1 |
|
№
варианта
|
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
| N |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
7 |
7 |
7 |
7 |
7 |
7 |
| K |
1 |
1 |
1 |
1 |
3 |
2 |
5 |
5 |
2 |
3 |
4 |
5 |
6 |
5 |
3 |
| L |
2 |
3 |
4 |
5 |
2 |
3 |
2 |
3 |
3 |
2 |
3 |
2 |
1 |
3 |
5 |
Решение:
Множество вершин
X
= {x1, x2, x3,
x4, x5,
x6 }, n = 6 k = 2, l = 1 Гxi=I±l.
а) определим исходный граф и
ассоциированный с ним неориентированный граф графическим, матричным и
аналитическим способами:
Определим граф аналитическим
способом:
Гx1
= { x1, x3,
x2
};
Гx2
= { x4, x1, x3 };
Гx3
= { x1, x5, x2,
x4
};
Гx4
= { x2, x6, x3, x5 };
Гx5
= { x3,
x4,
x6
};
Гx6
= {x4, x5 }.
Ориентированный граф графическим
способом:
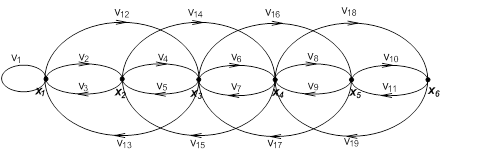
Неориентированный граф
графическим способом:
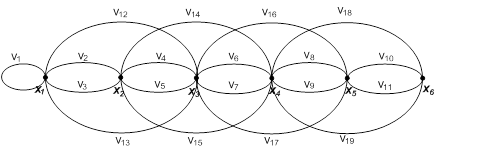
Ориентированный граф матричным
способом:
RG - матрица смежности 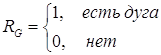
|
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
|
x1
|
1* |
1 |
1 |
0 |
0 |
0 |
|
x2
|
1 |
0 |
1 |
1 |
0 |
0 |
|
x3
|
1 |
1 |
0 |
1 |
1 |
0 |
|
x4
|
0 |
1 |
1 |
0 |
1 |
1 |
|
x5
|
0 |
0 |
1 |
1 |
0 |
1 |
|
x6
|
0 |
0 |
0 |
1 |
1 |
0 |
AG - матрица инцидентности 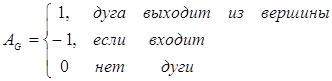
|
|
v1
|
v2
|
v3
|
v4
|
v5
|
v6
|
v7
|
v8
|
v9
|
v10
|
v11
|
v12
|
v13
|
v14
|
v15
|
v16
|
v17
|
v18
|
v19
|
|
x1
|
1* |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
x2
|
0 |
-1 |
1 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
-1 |
0 |
0 |
0 |
0 |
|
x3
|
0 |
0 |
0 |
-1 |
1 |
1 |
-1 |
0 |
0 |
0 |
0 |
-1 |
1 |
0 |
0 |
1 |
-1 |
0 |
0 |
|
x4
|
0 |
0 |
0 |
0 |
0 |
-1 |
1 |
1 |
-1 |
0 |
0 |
0 |
0 |
-1 |
1 |
0 |
0 |
1 |
-1 |
|
x5
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
1 |
1 |
-1 |
0 |
0 |
0 |
0 |
-1 |
1 |
0 |
0 |
|
x6
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
1 |
Неориентированный граф матричным
способом:
RD - матрица смежности
|
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
|
x1
|
1* |
2 |
2 |
0 |
0 |
0 |
|
x2
|
2 |
0 |
2 |
2 |
0 |
0 |
|
x3
|
2 |
2 |
0 |
2 |
2 |
0 |
|
x4
|
0 |
2 |
2 |
0 |
2 |
2 |
|
x5
|
0 |
0 |
2 |
2 |
0 |
2 |
|
x6
|
0 |
0 |
0 |
2 |
2 |
0 |
AD - матрица инцидентности
|
|
v1
|
v2
|
v3
|
v4
|
v5
|
v6
|
v7
|
v8
|
v9
|
v10
|
v11
|
v12
|
v13
|
v14
|
v15
|
v16
|
v17
|
v18
|
v19
|
|
x1
|
1* |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
x2
|
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
x3
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
x4
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
x5
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
x6
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
б) установить центры и
периферийные вершины графов, найти радиусы и диаметры графов:
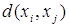 -
матрица отклонений имеет вид: -
матрица отклонений имеет вид:
|
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
|
x1
|
1 |
1 |
1 |
2 |
2 |
3 |
|
x2
|
1 |
0 |
1 |
1 |
2 |
2 |
|
x3
|
1 |
1 |
0 |
1 |
1 |
2 |
|
x4
|
2 |
1 |
1 |
0 |
1 |
1 |
|
x5
|
2 |
2 |
1 |
1 |
0 |
1 |
|
x6
|
3 |
2 |
2 |
1 |
1 |
0 |
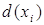 -
вектор отклонения -
вектор отклонения
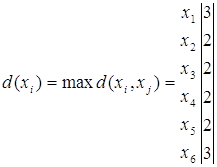 => =>
х2, х3,
х4, х5 - центры графа с наименьшей удаленностью.
Радиус ρ (G) = 2.
Периферийными вершинами являются
вершины х1, х6 с наибольшей
удаленностью. Диаметр графа D (G) = 3.
в) выделим в ориентированном
графе два подграфа и найдем объединение, пересечение и разность подграфов.
 
Выделяем два подграфа: G1 и G2
X1
- {x1, x2}, Г1х1 = {x1, x2},
Г1х2 = {x1},
X2
- {x1, x2, x3}, Г2х1 = {x2}, Г2х2 = {x3}, Г2х3 = {x2}.
Объединение 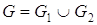 , ,
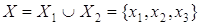 , ,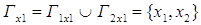 , , 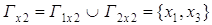 , , 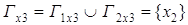 . .
G 
Пересечение
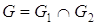 , ,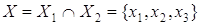 , ,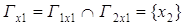 , , 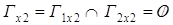 . .
G 
Разность
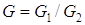 , ,
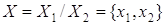 , , 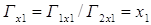 , , 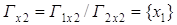 . .
G 
г) Считая, что передача между
вершинами xi и xj
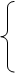 i*j при i ³ j; i*j при i ³ j;
Kij =
1/ (p+1) при i<j .
Сигнальный граф имеет вид
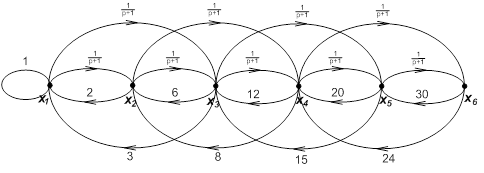
Система уравнений,
соответствующая сигнальному графу имеет вид
x1
= x1 +2x2 +3x3
x2
=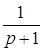 x1
+6 x3 +8 x4 x1
+6 x3 +8 x4
x3
=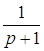 x1 + x1 +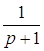 x2+12x4
+15x5 x2+12x4
+15x5
x4
= 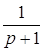 x2
+ x2
+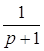 x3 +20 x5
+24x6 x3 +20 x5
+24x6
x5
= 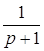 x3
+ x3
+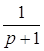 x4 +30x6 x4 +30x6
x6
=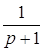 x4
+ x4
+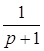 x5 x5
Определить передачу k16 по правилу Мезона. Формула
Мезона имеет вид
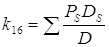
PS - передача пути,
DS - алгебраическое дополнение,
D - определитель.
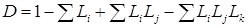
Пути из х1 в х6
и передаточные функции для каждого из них имеют вид:
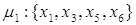 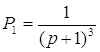
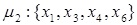 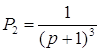
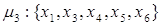 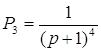
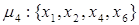 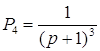
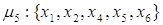 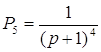
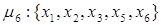 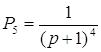
Контура:
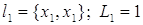 ; ;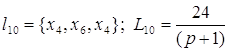
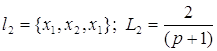 ; ;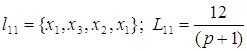 ; ;
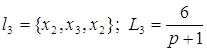 ; ;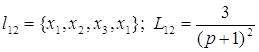 ; ;
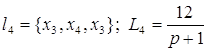 ; ;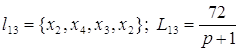 ; ;
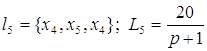 ; ;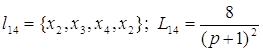 ; ;
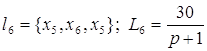 ; ;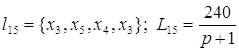 ; ;
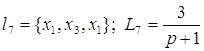 ; ;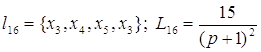
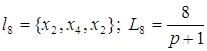 ; ;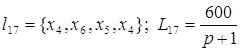 . .
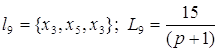 ; ;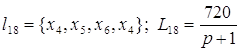 . .
Пары несоприкасающихся контуров
L1L3, L1L4, L1L5, L1L6, L1L8, L1L9, L1L10, L1L13, L1L14, L1L15, L1L16, L1L17, L1L18;
L2L4, L2L5, L2L6, L2L8, L2L9, L2L10, L2L15, L2L16, L2L17, L2L18;
L3L5, L3L6, L3L10, L3L17, L3L18;
L4L6, L5L7; L5L11, L5L12, L6L7, L6L8, L6L11, L6L12, L6L13, L6L14;
L7L8, L7L10, L7L17, L7L18;
L8L9, L9L10, L10L11, L10L12, L11L17, L11L18, L12L17, L12L18.
Независимые тройки
L1L3L5,
L1L3L6,
L1L3L10,
L1L3L17,
L1L3L18,
L1L4L6,
L1L6L8,
L1L6L13,
L1L6L14,
L1L8L9,L1L9L10,
L2L4L6, L2L9L10,
L6L7L8.
Отсюда
D
= 1 - (L1 +L2 +L3
+L4 +L5 + L6
+L7 + L8 +L9
+L10 +L11 +L12
+
+L13
+L14+L15 +L16+L17 +L18)+
(L1L3+L1L4+L1L5+L1L6+L1L8+L1L9+L1L10+L1L13+L1L14+L1L15+L1L16+L1L17+L1L18+L2L4+L2L5+L2L6+L2L8+L2L9+L2L10+L2L15+L2L16+L2L17+L2L18
+L3L5+L3L6+L3L10+L3L17+L3L18
L4L6+L5L7+L5L11+L5L12+L6L7+L6L8+L6L11+L6L12+L6L13+L6L14+L7L8+L7L10+L7L17+L7L18+L8L9+L9L10+L10L11+L10L12+L11L17+L11L18+L12L17+L12L18)
-
(L1L3L5+L1L3L6+L1L3L10+L1L3L17+L1L3L18+L1L4L6+L1L6L8+L1L6L13+L1L6L14+L1L8L9+L1L9L10+L2L4L6+L2L9L10+L6L7L8).
D1
= 1- L8;
D2
= 1;
D3
= 1;
D4
= 1 - L9;
D5
= 1;
D6
= 1.
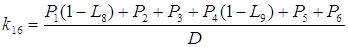 . .
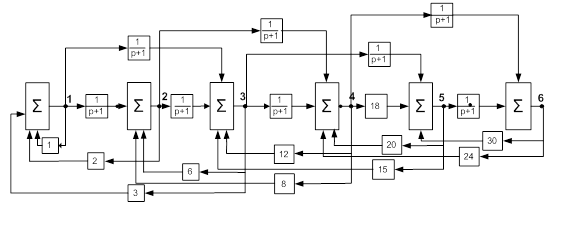
Структура кинематической системы
представлена на рисунке:
Задача 2. Задача о максимальном потоке и потоке минимальной стоимости
Транспортная сеть задана в виде
ориентированного графа, приведенного на рисунке.
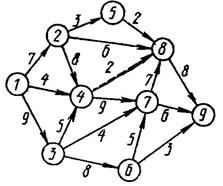
На каждом из ребер проставлены
значения пропускной способности С (n)
ребра n.
Для заданной сети определить
максимальный поток jmax транспортировки груза между указанной парой
вершин, считая одну из них источником, а другую — стоком.
Решение:
Максимальный поток jmax
транспортировки груза между указанной парой вершин, считая одну из них источником,
а другую — стоком:
Первый шаг.1. Находим какой-либо
путь из х1 в х9 с положительной пропускной
способностью.
Tаблица
1.
|
|
x1
|
x2 (1)
|
x3 (1)
|
x4 (1)
|
x5 (2)
|
x6 (3)
|
x7 (3)
|
x8 (2)
|
x9 (6)
|
|
x1
|
|
7 |
9-
|
4 |
|
|
|
|
|
|
x2
|
0 |
|
|
8 |
3 |
|
|
6 |
|
|
x3
|
0+
|
|
|
5 |
|
8-
|
4 |
|
|
|
x4
|
0 |
0 |
0 |
|
|
|
9 |
2 |
|
|
x5
|
|
0 |
|
|
|
|
|
2 |
|
|
x6
|
|
|
0+
|
|
|
|
5 |
|
3-
|
|
x7
|
|
|
0 |
0 |
|
0 |
|
7 |
6 |
|
x8
|
|
0 |
|
0 |
0 |
|
0 |
|
8 |
|
x9
|
|
|
|
|
|
0+
|
0 |
0 |
|
В результате получен путь l1
= (x1, х3, х6, х9). Элементы
этого пути Cij помечаем знаком минус, а симметричные элементы Cji
- знаком плюс.
Определяем пропускную способность
найденного пути, которая равна наименьшей из пропускных способностей дуг:
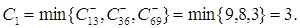
Определяем остаточные пропускные
способности дуг найденного пути и симметричных ему дуг. Для этого из элементов 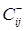 табл.1 вычитаем C1,
а к элементам табл.1 вычитаем C1,
а к элементам 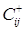 прибавляем C1.
В результате получим новую табл.2 с измененными пропускными способностями. прибавляем C1.
В результате получим новую табл.2 с измененными пропускными способностями.
Tаблица
2
|
|
x1
|
x2 (1)
|
x3 (1)
|
x4 (1)
|
x5 (2)
|
x6 (3)
|
x7 (3)
|
x8 (2)
|
x9 (7)
|
|
x1
|
|
7 |
6-
|
4 |
|
|
|
|
|
|
x2
|
0 |
|
|
8 |
3 |
|
|
6 |
|
|
x3
|
3+
|
|
|
5 |
|
5 |
4-
|
|
|
|
x4
|
0 |
0 |
0 |
|
|
|
9 |
2 |
|
|
x5
|
|
0 |
|
|
|
|
|
2 |
|
|
x6
|
|
|
3 |
|
|
|
5 |
|
0 |
|
x7
|
|
|
0+
|
0 |
|
0 |
|
7 |
6-
|
|
x8
|
|
0 |
|
0 |
0 |
|
0 |
|
8 |
|
x9
|
|
|
|
|
|
3 |
0+
|
0 |
|
Второй шаг.1. Помечаем
столбцы табл.2, находим второй путь l2 = (x1,x3,
х7, х9) и расставляем знаки.
2. Пропускная способность пути l2
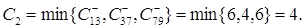
Изменим пропускные способности
помеченных дуг на С2 в табл.3.
Tаблица
3
|
|
x1
|
x2 (1)
|
x3 (1)
|
x4 (1)
|
x5 (2)
|
x6 (3)
|
x7 (4)
|
x8 (2)
|
x9 (7)
|
|
x1
|
|
7 |
2 |
4-
|
|
|
|
|
|
|
x2
|
0 |
|
|
8 |
3 |
|
|
6 |
|
|
x3
|
7 |
|
|
5 |
|
5 |
0 |
|
|
|
x4
|
0+
|
0 |
0 |
|
|
|
9-
|
2 |
|
|
x5
|
|
0 |
|
|
|
|
|
2 |
|
|
x6
|
|
|
3 |
|
|
|
5 |
|
0 |
|
x7
|
|
|
4 |
0+
|
|
0 |
|
7 |
2-
|
|
x8
|
|
0 |
|
0 |
0 |
|
0 |
|
8 |
|
x9
|
|
|
|
|
|
3 |
4+
|
0 |
|
Третий шаг.1. Пометив столбцы,
находим l3 = (x1, х4, х7,x9).
Величина потока по пути l3
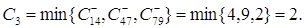
Вычислив новые пропускные
способности дуг, приходим к табл.4.
Таблица 4
|
|
x1
|
x2 (1)
|
x3 (1)
|
x4 (1)
|
x5 (2)
|
x6 (3)
|
x7 (4)
|
x8 (2)
|
x9 (8)
|
|
x1
|
|
7-
|
2 |
2 |
|
|
|
|
|
|
x2
|
0+
|
|
|
8 |
3 |
|
|
6-
|
|
|
x3
|
7 |
|
|
5 |
|
5 |
0 |
|
|
|
x4
|
2 |
0 |
0 |
|
|
|
7 |
2 |
|
|
x5
|
|
0 |
|
|
|
|
|
2 |
|
|
x6
|
|
|
3 |
|
|
|
5 |
|
0 |
|
x7
|
|
|
4 |
2 |
|
0 |
|
7 |
0 |
|
x8
|
|
0+
|
|
0 |
0 |
|
0 |
|
8-
|
|
x9
|
|
|
|
|
|
3 |
6 |
0+
|
|
Четвертый шаг.1. Помечаем
столбцы табл.4, находим четвертый путь l4 = (x1,
х2, х8, х9) и расставляем знаки.
2. Пропускная способность пути l4
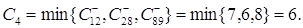
Изменим пропускные способности
помеченных дуг на С4 в табл.5.
Таблица 5
|
|
x1
|
x2 (1)
|
x3 (1)
|
x4 (1)
|
x5 (2)
|
x6 (3)
|
x7 (4)
|
x8 (4)
|
x9 (8)
|
|
x1
|
|
1 |
2 |
2-
|
|
|
|
|
|
|
x2
|
6 |
|
|
8 |
3 |
|
|
0 |
|
|
x3
|
7 |
|
|
5 |
|
5 |
0 |
|
|
|
x4
|
2+
|
0 |
0 |
|
|
|
7 |
2-
|
|
|
x5
|
|
0 |
|
|
|
|
|
2 |
|
|
x6
|
|
|
3 |
|
|
|
5 |
|
0 |
|
x7
|
|
|
4 |
2 |
|
0 |
|
7 |
0 |
|
x8
|
|
6 |
|
0+
|
0 |
|
0 |
|
2-
|
|
x9
|
|
|
|
|
|
3 |
6 |
6+
|
|
Пятый шаг.1. Помечаем столбцы
табл.5, находим четвертый путь l5 = (x1, х4,
х8, х9) и расставляем знаки.
2. Пропускная способность пути l5
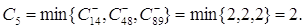
Изменим пропускные способности
помеченных дуг на С5 в табл.6.
Таблица 6
|
|
x1
|
x2 (1)
|
x3 (1)
|
x4 (1)
|
x5 (2)
|
x6 (3)
|
x7 (4)
|
x8 (5)
|
x9
|
|
x1
|
|
1 |
2 |
0 |
|
|
|
|
|
|
x2
|
6 |
|
|
8 |
3 |
|
|
0 |
|
|
x3
|
7 |
|
|
5 |
|
5 |
0 |
|
|
|
x4
|
4 |
0 |
0 |
|
|
|
7 |
0 |
|
|
x5
|
|
0 |
|
|
|
|
|
2 |
|
|
x6
|
|
|
3 |
|
|
|
5 |
|
0 |
|
x7
|
|
|
4 |
2 |
|
0 |
|
7 |
0 |
|
x8
|
|
6 |
|
2 |
0 |
|
0 |
|
0 |
|
x9
|
|
|
|
|
|
3 |
6 |
8 |
|
Шестой шаг. Просматривая строки
и помечая столбцы, убеждаемся в том, больше не существует ни одного пути с
положительной пропускной способностью из вершины x1
в вершину x9. Подмножество R
образуют помеченные вершины х1, х2,
х3, х4, х5, х6,
х7, х8, а подмножество 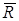 - одна непомеченная
вершины х9. Разрез с минимальной пропускной способностью
образуют дуги, начальные вершины которых принадлежат подмножеству R, а
конечные - - одна непомеченная
вершины х9. Разрез с минимальной пропускной способностью
образуют дуги, начальные вершины которых принадлежат подмножеству R, а
конечные - 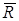 . Таким образом, разрез с
минимальной пропускной способностью . Таким образом, разрез с
минимальной пропускной способностью 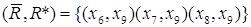 .
Удалив дуги этого разреза, блокируем все пути из источника в сток. Пропускная
способность разреза .
Удалив дуги этого разреза, блокируем все пути из источника в сток. Пропускная
способность разреза
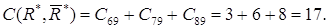
Заключительный шаг. Вычитая из
элементов табл.1 соответствующие элементы табл.6, получим табл.7
Таблица 7.
|
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x7
|
x8
|
x9
|
|
x1
|
|
6 |
7 |
4 |
|
|
|
|
|
|
x2
|
-6 |
|
|
0 |
0 |
|
|
6 |
|
|
x3
|
-7 |
|
|
0 |
|
3 |
4 |
|
|
|
x4
|
-4 |
0 |
0 |
|
|
|
2 |
2 |
|
|
x5
|
|
0 |
|
|
|
|
|
0 |
|
|
x6
|
|
|
-3 |
|
|
|
0 |
|
3 |
|
x7
|
|
|
4 |
2 |
|
0 |
|
0 |
6 |
|
x8
|
|
-6 |
|
-2 |
0 |
|
0 |
|
8 |
|
x9
|
|
|
|
|
|
-3 |
-6 |
-8 |
|
Величина максимального потока
равна сумме элементов x1-й
строки табл.7 или сумме элементов x9-го
столбца.
Максимальный поток равен 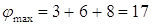 . .
Задача 3. Анализ сетей Петри
Сеть Петри задана графически
(рис.23…30). В табл.1 в соответствии с вариантом и указанным номером рисунка
приведены различные начальные маркировки сети.
Выполнить следующие действия:
Описать сеть аналитическим и
матричным способами.
Проверить условия срабатывания
каждого из переходов и найти новые маркировки, к которым приведет срабатывание
соответствующих переходов, путем выполнения матричных преобразований.
Построить дерево достижимости
заданной сети.
Проверить, является ли
достижимой одна из маркировок, получаемых на четвертом шаге построения дерева,
составив и решив матричные уравнения.
Таблица 1
|
№
варианта
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| m1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
2 |
2 |
0 |
1 |
3 |
0 |
1 |
1 |
| m2 |
1 |
2 |
2 |
2 |
3 |
1 |
2 |
2 |
1 |
2 |
3 |
1 |
1 |
2 |
0 |
| m3 |
2 |
3 |
1 |
0 |
1 |
1 |
1 |
3 |
2 |
1 |
0 |
1 |
2 |
3 |
3 |
| m4 |
3 |
1 |
3 |
4 |
0 |
2 |
1 |
1 |
0 |
1 |
1 |
2 |
1 |
1 |
2 |
| m5 |
1 |
2 |
5 |
1 |
2 |
2 |
3 |
0 |
3 |
3 |
2 |
0 |
3 |
2 |
1 |
| № рисунка |
Рис.23 |
Рис.27 |
Рис.28 |
Рис.29 |
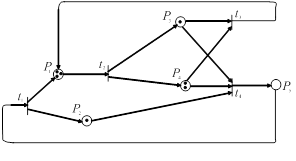
Решение:
Опишем сеть аналитическим и
матричным способами. Приведем графическое представление сети Петри, в которой
позиции P = {p1, p2, p3, p4, p5}
и переходы T = {t1, t2, t3 , t4 }.
Начальная маркировка сети
обозначается вектором μ0 [μ1,μ2,μ3,μ4,μ5],
μ0 [1 3 0 1 2]. Отсюда получим:
При аналитическом способе
задания сеть Петри задается как C = (P,T,F,H,μ0), где,
кроме множеств позиций Р и переходов Т, задаются входная F
и выходная Н функции.
Через F (tj) обозначается множество входных позиций, а
через H (tj) -
множество выходных позиций перехода tj;
μ0 - начальная маркировка
сети.
F (t1)
= {p5},H (t1) = {p1, p2 },
F (t2)
= {p1},H (t2) = {p3, p4},
F (t3)
= {p3, p4}H (t3) = {p1 },
F
(t4) = {p2, p3,
p4}H
(t4) = {p5 }.
μ0 [1 3 0
1 2]
Матричная форма определения сети
Петри эквивалентна аналитическому способу задания C
= (P,T,D-,D+,μ0).
Здесь D- и D+ - матрицы входных и выходных
инциденций соответственно размером m × n, где m -
число переходов и n -
число позиций.
Элемент dij-
матрицы D- равен кратности
дуг, входящих в i-й переход из j-й позиции.
Элемент dij+
матрицы D+ равен кратности
дуг, выходящих из i-ro
перехода в j-ю позицию.
Для рассматриваемой сети Петри
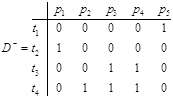 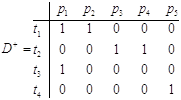
 
Матрица D
= D+ - D -
называется матрицей инцидентности сети Петри,
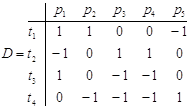
2. При начальной маркировке μ0
[1 3 0 1 2] сети Петри разрешенными являются переходы t1
и t2.
Условия срабатывания для
перехода t3 и t4 не выполняется.
Переход t1
[μ0] ≥ [1000]*
D- = [1000] · 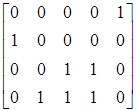 ; [1 3 0 1 2]
≥ [00001] – ; [1 3 0 1 2]
≥ [00001] –
условие выполняется, переход
разрешен.
Новая маркировка при
срабатывании перехода t1 равна:
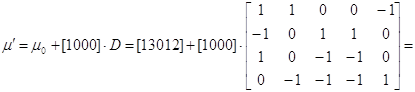
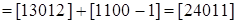 . .
Переход t2
[μ0] ≥ [0100]*
D- = [0100] 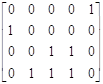 ·;[1 3 0 1 2]
≥ [10000] – ·;[1 3 0 1 2]
≥ [10000] –
условие выполняется, переход
разрешен.
Новая маркировка при
срабатывании перехода t2 равна:
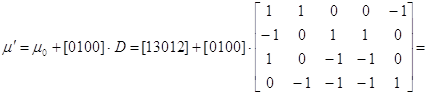
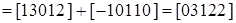 . .
Переход t3
[μ0] ≥ [0010]*
D- = [0010] 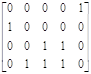 ·;[1 3 0 1 2]
≥ [00110] - условие не ·;[1 3 0 1 2]
≥ [00110] - условие не
выполняется, переход запрещен.
Переход t4
[μ0] ≥ [0001]*
D- = [0001] 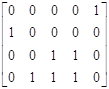 ·;[1 3 0 1 2]
≥ [01110] – ·;[1 3 0 1 2]
≥ [01110] –
условие не выполняется, переход
запрещен.
Построим дерево достижимости
заданной сети.
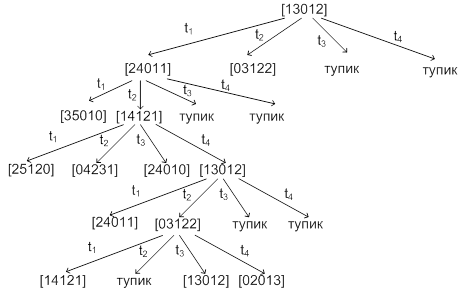
Проверим, является ли достижимой
одна из маркировок, полученных на пятом шаге построения дерева, составив и
решив матричные уравнения.
Уравнение 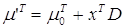 принимает вид принимает вид
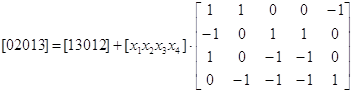
Перенесем 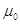 в левую часть и выполним
умножение, тогда в левую часть и выполним
умножение, тогда
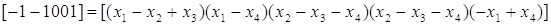 . .
Приравняем составляющие векторов
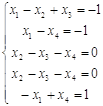
Система имеет решение x1 = 1; x2
= 2; x3 = 0; x4 = 2.
Это значит, что исследуемая
маркировка достижима и в последовательности срабатываний переход t1 срабатывает один раз,
переходы t2 и t4 - по два раза, переход t3 не срабатывает.
Задача 4. Элементы математической логики и теории автоматов
Конечный автомат задан графом,
определенным в задаче 1. Вершины графа отождествляются с состояниями автомата
таким образом, что множество состояний Q = {q1,
q2 ,…, qn}. Переход автомата из одного состояния в
другое осуществляется под воздействием множества входных сигналов X={x1,
x2, x3, x4}.
Переходы определяются законом отображения Г вершин графа, причем каждому
переходу соответствует только одна из букв множества X.
При задании графа эти буквы расставить произвольно.
Автомат позволяет вырабатывать
выходные сигналы Y={y1,
y2, y3}:
y1
- переход из состояния qi в состояние
qi (петля);
y2
- переход из состояния qi в qj при i<j;
y3
- переход из состояния qi в qj при i>j.
Осуществить структурный синтез
конечного автомата. Реализацию осуществить на элементах, указанных в табл.1, в
соответствии с номером варианта. Обязательной является минимизация реализуемых
функций.
Таблица 1
|
№
варианта
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Тип
элементов
|
И
НЕ
|
И
ИЛИ
НЕ
|
И
НЕ
|
ИЛИ
НЕ
|
И
НЕ
|
И
ИЛИ
НЕ
|
И
НЕ
|
ИЛИ
НЕ
|
И
ИЛИ
НЕ
|
И
НЕ
|
|
Тип
триггера
|
D |
JK |
T |
D |
RS |
RSD |
D |
JK |
T |
D |
Решение:
Множество вершин X = {x1,
x2, x3, x4,
x5, x6},
Вершины графа отожествляются с
состояниями автомата таким образом, что множество состояний Q = {q1,
q2, q3,
q4, q5,
q6}. Переход автомата из
одного состояния в другое осуществляется под воздействием множества входных
сигналов X={x1,
x2, x3, x4}.
Автомат позволяет вырабатывать
выходные сигналы Y={y1,
y2, y3}.
На основании аналитического
описания ориентированного графа из задания № 1 запишем закон отображения
состояний автомата:
Гq1
= {q1 (x1/y1),
q3 (x2/y2), q2 (x3/y2)},
Гq2
= {q4 (x3/y2),
q1 (x4/y3), q3 (x1/y2)},
Гq3
= {q1 (x1/y3),
q5 (x2/y2), q2 (x3/y3),
q4 (x4/y2)},
Гq4
= {q2 (x1/y3),
q6 (x2/y2), q3 (x3/y3),
q5 (x4/y2)},
Гq5
= {q3 (x4/y3),
q4 (x1/y3), q6 (x2/y2)}, Гq6
= {q4 (x3/y3),
q5 (x4/y3)}.
Обобщенная таблица переходов и
выходов соответствующего конечного автомата представлена в табл.2.
Таблица 2
| X |
Q |
q1
|
q2
|
q3
|
q4
|
q5
|
q6
|
|
X1
|
q1/y1
|
q3/y2
|
q1/y3
|
q2/y3
|
q4/y3
|
─ |
|
X2
|
q3/y2
|
─ |
q5/y2
|
q6/y2
|
q6/y2
|
─ |
|
X3
|
q2/y2
|
q4/y2
|
q2/y3
|
q3/y3
|
─ |
q4/y3
|
|
X4
|
─ |
q1/y3
|
q4/y2
|
q5/y2
|
q3/y3
|
q5/y3
|
Осуществим структурный синтез
автомата, заданного табл.1. В качестве элементов памяти используем D-триггеры, в качестве элементной базы используем логические
элементы И-НЕ.
Количество букв входного
алфавита n = 4
Количество входовp ≥ log2
n = log2 4 =
2;
Количество букв выходного
алфавита m = 2
Количество выходовe ≥ log2
m = log2 3 =
2;
Количество состояний r = 6
Количество триггеровz ≥ log2
r = log2 6 =
3.
Приступаем к кодированию:
x
|
u |
u1
|
u2
|
|
|
x1
|
1 |
0 |
5 |
|
x2
|
1 |
1 |
4 |
|
x3
|
0 |
0 |
5 |
|
x4
|
0 |
1 |
5 |
|
|
v1
|
v2
|
|
|
y1
|
1 |
0 |
1 |
|
y2
|
0 |
1 |
9 |
|
y3
|
0 |
0 |
9 |
| q |
w |
w1
|
w2
|
w3
|
|
|
q1
|
0 |
0 |
1 |
3 |
|
q2
|
0 |
1 |
0 |
3 |
|
q3
|
0 |
0 |
0 |
4 |
|
q4
|
1 |
0 |
0 |
4 |
|
q5
|
0 |
1 |
1 |
3 |
|
q6
|
1 |
1 |
0 |
2 |
На основании результатов
кодирования строим обобщенную таблицу переходов и выходов структурного автомата
(табл.3), заменяя состояния, входные и выходные переменные их кодами.
Таблица 3
|
u1u2
|
w1w2w3
|
001 |
010 |
000 |
100 |
011 |
110 |
| 10 |
001/10 |
000/01 |
001/00 |
010/00 |
100/00 |
─ |
| 11 |
000/01 |
─ |
011/01 |
110/01 |
110/01 |
─ |
| 00 |
010/01 |
100/01 |
010/00 |
000/00 |
─ |
100/00 |
| 01 |
─ |
001/00 |
100/01 |
011/01 |
000/00 |
011/00 |
Используя таблицу переходов D-триггера и данные предыдущей таблицы, составим обобщенную
таблицу функционирования структурного автомата (табл.4). Функции возбуждения
трех триггеров обозначены через D1, D2, D3,
соответственно.
Таблица 4
|
u1
|
u2
|
w1 (t)
|
w2 (t)
|
w3 (t)
|
w1
(t+1)
|
w2
(t+1)
|
w3
(t+1)
|
v1
|
v2
|
D1
|
D2
|
D3
|
| 1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
| 1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
| 0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
| 0 |
1 |
0 |
0 |
1 |
* |
* |
* |
* |
* |
* |
* |
* |
| 1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
| 1 |
1 |
0 |
1 |
0 |
* |
* |
* |
* |
* |
* |
* |
* |
| 0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
| 0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
| 1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
| 1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
| 0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
| 0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
| 1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
| 1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
| 0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
| 1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
| 1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
| 0 |
0 |
0 |
1 |
1 |
* |
* |
* |
* |
* |
* |
* |
* |
| 0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
1 |
1 |
0 |
* |
* |
* |
* |
* |
* |
* |
* |
| 1 |
1 |
1 |
1 |
0 |
* |
* |
* |
* |
* |
* |
* |
* |
| 0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
| 0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
По этой таблице запишем СДНФ
выходных функций V и функций возбуждения триггеров D1,
D2, и D3,
зависящих от набора переменных u1, u2, w1 (t),
w2 (t), w3 (t). В результате получим систему логических
функций для построения комбинационной части автомата:
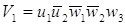 . .
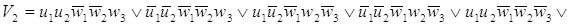
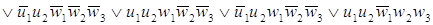 . .
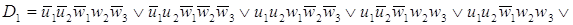
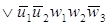 . .
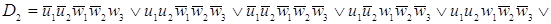
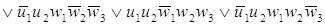 . .
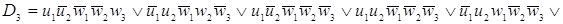
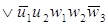 . .
Минимизируем функции согласно
картам Карно:
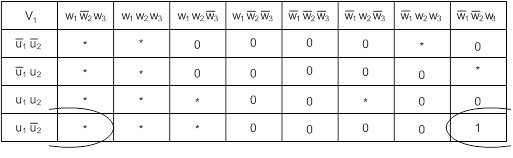
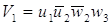
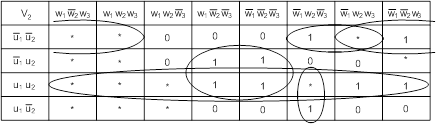
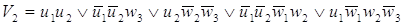

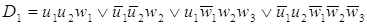
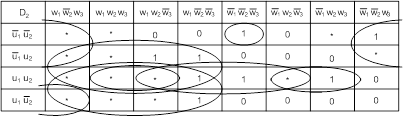
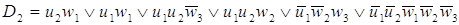
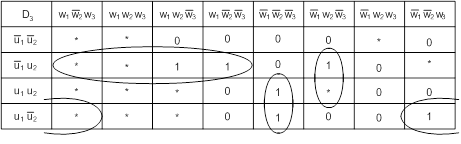
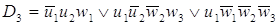
После минимизации имеем набор
функций в базисе И-НЕ
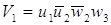
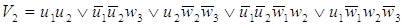 = =
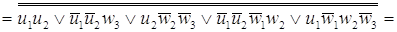
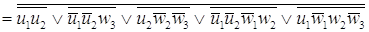 . .
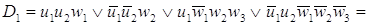
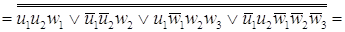
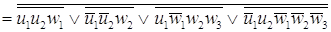 . .
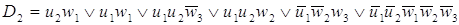
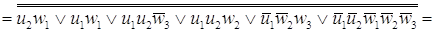
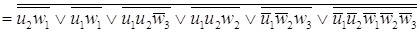
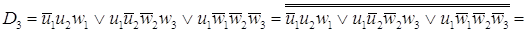
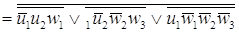 . .
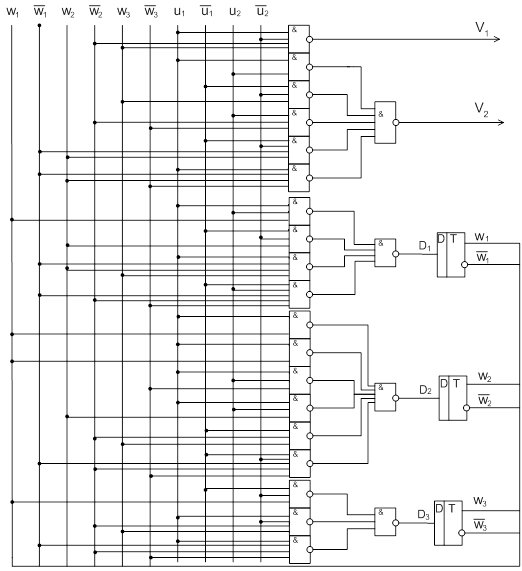
Функциональная схема
структурного автомата:
|