Курсовая работа: Анализ радиосигналов и расчет характеристик оптимальных согласованных фильтров
Курсовая работа: Анализ радиосигналов и расчет характеристик оптимальных согласованных фильтров
Министерство общего и профессионального образования Российской
Федерации
УГТУ-УПИ имени С.М. Кирова
кафедра
Теоретические основы радиотехники
АНАЛИЗ РАДИОСИГНАЛОВ И РАСЧЕТ ХАРАКТЕРИСТИК ОПТИМАЛЬНЫХ
СОГЛАСОВАННЫХ ФИЛЬТРОВ
КУРСОВОй ПРОЕКТ
ЕКАТЕРИНБУРГ 2001 год
Содержание
Реферат
Введение
Расчёт акф заданного сигнала
Расчёт спектральной плотности и энергетического спектра
Расчёт импульсной реакции и рекомендации к построению
согласованного фильтра
Заключение
Перечень условных обозначений
Библиографический список
Информация ценилась всегда, а с
развитием человечества информации становится все больше и больше. Информационные
потоки превратились в огромные реки.
В связи с этим возникло
несколько проблем передачи информации.
Информацию всегда ценили за ее
достоверность и полноту поэтому ведется борьба за передачу ее без потерь и
искажения. С еще одной проблемой при выборе оптимального сигнала.
Все это переносится и на радиотехнику
где разрабатываются приемные передающее и обрабатывающие эти сигналы. Скорость
и сложность предаваемых сигналов постоянно усложняется оборудование.
Для получения и закрепления
знаний по обработке простейших сигналов в учебном курсе есть практическое
задание.
В данной курсовой работе
рассматривается прямоугольная когерентная пачка, состоящая из N трапецеидальных
(длительность вершины равна одной третьей длительности основания) радиоимпульсов,
где:
а) несущая частота,1,11МГц
б) длительность импульса (длительность
основания),15мкс
в) частота следования,11.2 кГц
г) число импульсов в пачке,9
Для заданного типа сигнала
необходимо произвести (привести):
Расчёт АКФ
Расчет спектра амплитуд и
энергетического спектра
Расчет импульсной
характеристики, согласованного фильтра
Рекомендации по построению
согласованного фильтра.
Спектральная плотность - есть
коэффициент пропорциональности между длиной малого интервала частот Df и отвечающей ему комплексной
амплитудой гармонического сигнала DA
с частотой f0.
Спектральное представление
сигналов открывает прямой путь к анализу прохождению сигналов через широкий
класс радиотехнических цепей, устройств и систем.
Энергетический спектр полезен
для получения различных инженерных оценок, устанавливающих реальную ширину
спектра того или иного сигнала. Для количественного определения степени отличия
сигнала U (t) и его смещенной во времени копии U (t-t) принято вводить АКФ.
Зафиксируем произвольный момент
времени 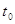 и постараемся так выбрать
функцию и постараемся так выбрать
функцию 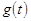 , чтобы величина , чтобы величина 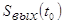 достигала максимально
возможного значения. Если такая функция действительно существует, то отвечающий
ей линейный фильтр называют согласованным фильтром. достигала максимально
возможного значения. Если такая функция действительно существует, то отвечающий
ей линейный фильтр называют согласованным фильтром.
Курсовая работа по
заключительной части предмета "Теория радиотехнических сигналов и цепей"
охватывает разделы курса, посвященного основам теории сигналов и их оптимальной
линейной фильтрации.
Целями работы являются:
изучение временных и
спектральных характеристик импульсных радиосигналов, применяемых в
радиолокации, радионавигации, радио телеметрии и смежных областях;
приобретение навыков по расчету
и анализу корреляционных и спектральных характеристик детерминированных
сигналов (автокорреляционных функций, спектров амплитуд и энергетических
спектров).
В курсовой работе для заданного
типа сигнала необходимо произвести:
Расчет АКФ.
Расчет спектра амплитуд и
энергетического спектра.
Импульсной характеристики
согласованного фильтра.
В данной курсовой работе
рассматривается прямоугольная когерентная пачка трапецеидальных радиоимпульсов.
Параметры сигнала:
несущая частота (частота радиозаполнения),1,11
МГц
длительность импульсов, (длительность
основания) 15 мкс
частота следования,11,2 кГц
число импульсов в пачке,9
Автокорреляционная функция (АКФ)
сигнала U (t) служит для количественного определения степени отличия
сигнала U (t) и его смещённой во времени копии 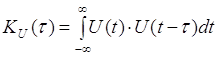 (0.1) и при t = 0 АКФ становится равной энергии
сигнала. АКФ обладает простейшими свойствами: (0.1) и при t = 0 АКФ становится равной энергии
сигнала. АКФ обладает простейшими свойствами:
свойство чётности:
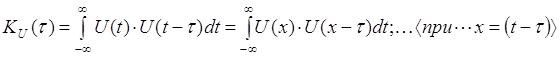 т.е. KU
(t) =KU (-t). т.е. KU
(t) =KU (-t).
при любом значении временного
сдвига t модуль АКФ не
превосходит энергии сигнала: ½KU
(t) ½£KU
(0), что вытекает из неравенства Коши - Буняковского.
Итак, АКФ представляется
симметричной кривой с центральным максимумом, который всегда положителен, а в
нашем случае АКФ имеет ещё и колебательный характер. Необходимо отметить, что
АКФ имеет связь с энергетическим спектром сигнала: 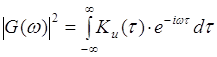 ; (0.2) где ½G (w) ½ ; (0.2) где ½G (w) ½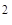 квадрат модуля
спектральной плотности. Поэтому можно оценивать корреляционные свойства
сигналов, исходя из распределения их энергии по спектру. Чем шире полоса частот
сигнала, тем уже основной лепесток автокорреляционной функции и тем совершеннее
сигнал с точки зрения возможности точного измерения момента его начала. квадрат модуля
спектральной плотности. Поэтому можно оценивать корреляционные свойства
сигналов, исходя из распределения их энергии по спектру. Чем шире полоса частот
сигнала, тем уже основной лепесток автокорреляционной функции и тем совершеннее
сигнал с точки зрения возможности точного измерения момента его начала.
Часто удобнее вначале получить
автокорреляционую функцию, а затем, используя преобразование Фурье, найти
энергетический спектр сигнала. Энергетический спектр - представляет собой
зависимость ½G (w) ½ от частоты. от частоты.
Согласованные же с сигналом
фильтры обладают следующими свойствами:
Сигнал на выходе согласованного
фильтра и функция корреляции выходного шума имеют вид автокорреляционной
функции полезного входного сигнала.
Среди всех линейных фильтров
согласованный фильтр даёт на выходе максимальное отношение пикового значения
сигнала к среднеквадратичному значению шума.
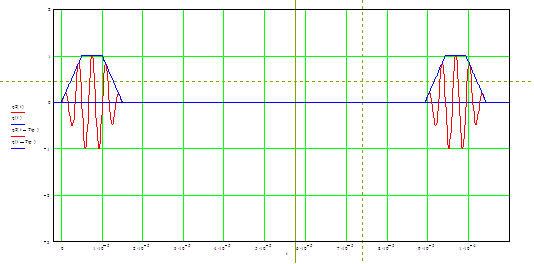
Рис.1. Прямоугольная когерентная пачка трапецеидальных
радиоимпульсов
В нашем случае сигнал представляет
собой прямоугольную пачку трапецеидальных (длительность вершины равна одной
третьей длительности основания) радиоимпульсов (см. рис 1) в которой
число импульсов N=9, а длительность импульса Ti=15 мкс.

Рис.2. Сдвиг копии огибающей сигнала
Период следования импульсов в пачке Tip » 89,286 мкс., поэтому скважность q = Tip/Ti
= 5,952. Для расчёта АКФ воспользуемся формулой (0.1) и графическим
представлением смещённой по времени копии сигнала на примере одного
трапецеидального импульса (огибающей). Для этого обратимся к рисунку 2. Для
расчёта главного лепестка АКФ огибающей сигнала (трапеции) рассмотрим три
промежутка:
Для величины сдвига T
принадлежащего промежутку от нуля до одной третьей длительности импульса
необходимо решить интеграл:
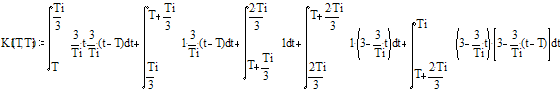
Решая этот интеграл, получаем выражение для главного
лепестка АКФ данного сдвига копии огибающей сигнала:
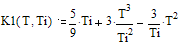
Для T принадлежащего промежутку
от одной третьей до двух третьих длительности импульса получаем следующий
интеграл:
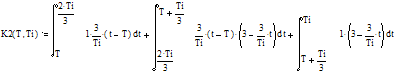
Решая его, получаем:
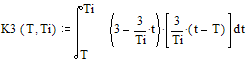 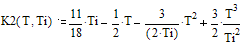
Для Т, принадлежащего промежутку
от двух третьих длительности импульса до длительности импульса интеграл, имеет
вид:
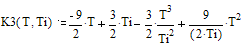
Поэтому в результате решения
имеем:
С учётом свойства симметрии (чётности)
АКФ (смотрите введение) и соотношения, связывающего АКФ радиосигнала и АКФ его
комплексной огибающей: 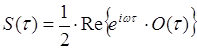 имеем
функции для главного лепестка АКФ огибающей ko (T) радиоимпульса и АКФ
радиоимпульса Ks (T): имеем
функции для главного лепестка АКФ огибающей ko (T) радиоимпульса и АКФ
радиоимпульса Ks (T):
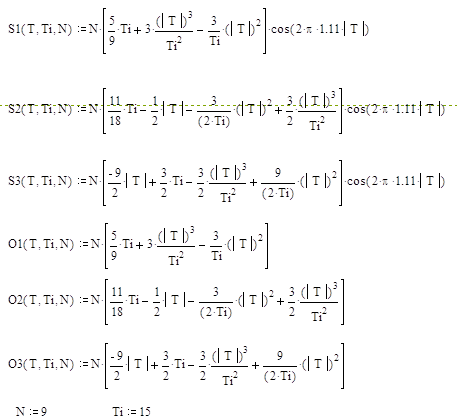

в которых, входящие функции,
имеют вид:
Таким образом, на рисунке 3 изображён
главный лепесток АКФ радиоимпульса и его огибающей, т.е. когда в результате
сдвига копии сигнала, когда участвуют все 9 импульсов пачки, т.е. N = 9.
Видно, что АКФ радиоимпульса
имеет колебательный характер, но в центре обязательно максимум. При дальнейшем
сдвиге число пересекающихся импульсов сигнала и его копии будет уменьшаться на
единицу, а, следовательно, и амплитуда через каждый период следования Tip
= 89,286 мкс.
Поэтому, окончательно АКФ будут
иметь вид как на рисунке 4 (16 лепестков, отличающихся от главного
только амплитудами) с учётом того, что на этом рисунке Т=Tip.:
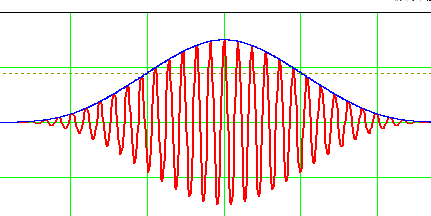
Рис. 3. АКФ главного лепестка радиоимпульса и его огибающей
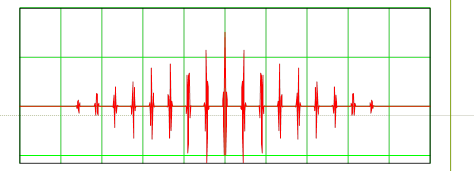
Рис. 4. АКФ Прямоугольной когерентной пачки трапецеидальных
радиоимпульсов
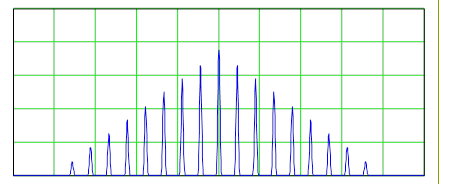
Рис. 5. Огибающая пачки радиоимпульсов.
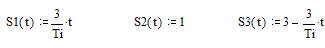
Для расчёта спектральной
плотности воспользуемся, как и при расчётах АКФ, функциями огибающей
радиосигнала (смотрите рис.2), которые имеют вид:
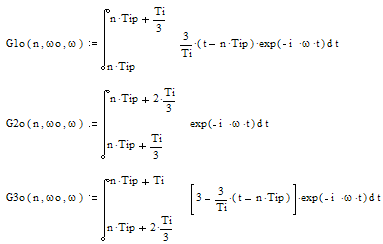
и преобразованием Фурье для
получения спектральных функций, которые с учётом пределов интегрирования для
n-го импульса будут рассчитываться по формулам:

для огибающей радиоимпульса и:
для радиоимпульса соответственно.
Далее вычисляем спектральную
плотность огибающей радиосигнала для всех N импульсов в соответствии с
выражением:
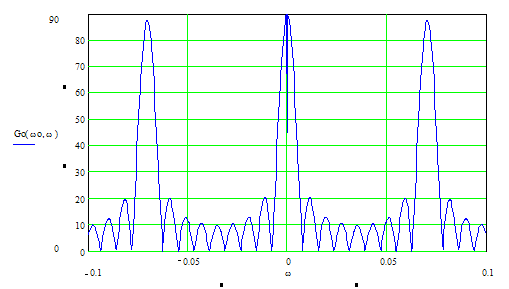
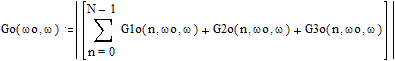
График этой функции представлен
на (рис.5).
на рисунке для наглядности
рассмотрен разный частотный диапазон
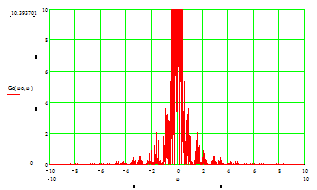
Рис. 6. Спектральная плотность огибающей радиосигнала.
Как и ожидалось, главный
максимум расположен в центре, т.е. при частоте w
=0.
Энергетический же спектр равен
квадрату спектральной плотности 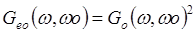 и
поэтому график спектра имеет вид как на (рис 6) т.е. очень похож на
график спектральной плотности: и
поэтому график спектра имеет вид как на (рис 6) т.е. очень похож на
график спектральной плотности:
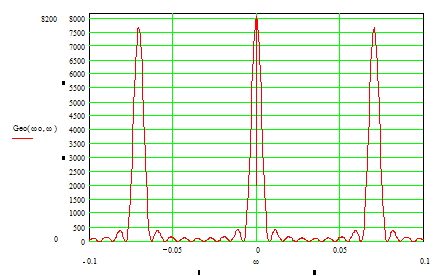
Рис. 7. Энергетический спектр огибающей радиосигнала.
Вид спектральной плотности для
радиосигнала будет иной, поскольку вместо одного максимума при w = 0 будет наблюдаться два максимума при w = ±
wо, т.е. спектр видеоимпульса (огибающей
радиосигнала) переносится в область высоких частот с уменьшением вдвое
абсолютного значения максимумов (см. рис.7). Вид энергетического же
спектра радиосигнала будет так же очень похож на вид спектральной плотности
радиосигнала, т.е. тоже будет осуществлён перенос спектра в область высоких
частот и так же будет наблюдаться два максимума (см. рис.8).
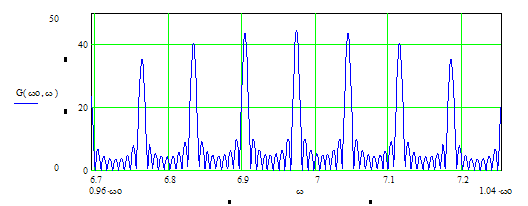
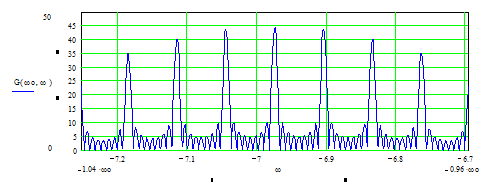
Рис. 8. Спектральная плотность пачки радиоимпульсов.
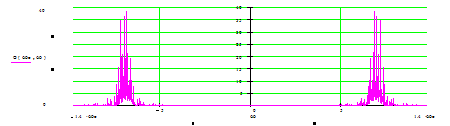
Рис. 9.
Как известно, наряду с полезным
сигналом, зачастую присутствуют шумы и поэтому при слабом полезном сигнале
иногда трудно определить есть полезный сигнал или нет.
Для приёма сигнала сдвинутого во
времени 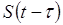 на фоне белого гауссовского
шума (белый гауссовский шум "БГС" имеет равномерную плотность
распределения) n (t) т.е. y (t) = на фоне белого гауссовского
шума (белый гауссовский шум "БГС" имеет равномерную плотность
распределения) n (t) т.е. y (t) =  +
n (t), отношение правдоподобия при приёме сигнала известной формы имеет вид: +
n (t), отношение правдоподобия при приёме сигнала известной формы имеет вид:
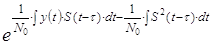
где No - спектральная плотность
шума.
Поэтому приходим к выводу, что
оптимальная обработка принимаемых данных - суть корреляционный интеграл
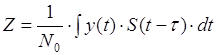
Полученная функция представляет
собой ту существенную операцию, которую следует выполнить над наблюдаемым
сигналом с тем, чтобы оптимальным (с позиции критерия минимума среднего риска) образом
принять решение о наличии или отсутствии полезного сигнала.
Не вызывает сомнений тот факт,
что данная операция может быть реализована линейным фильтром.
Действительно, сигнал на выходе
фильтра с импульсной характеристикой g (t) имеет вид:
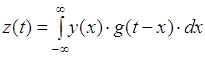
Как видно, при выполнении
условия g (r-x) = K×S (r-t) эти выражения эквивалентны и тогда
после замены t = r-x получаем:
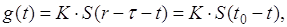
где К - постоянная, а to
- фиксированное время, при котором наблюдается выходной сигнал.
Фильтр с такой импульсной
характеристикой g (t) (смотрите выше) называется согласованным.
Для того чтобы определить
импульсную характеристику необходимо сигнал S (t) сместить на tо
влево, т.е. получим функцию S (tо + t), а функцию S (tо - t) получить
путём зеркального отображения сигнала относительно оси координат, т.е. импульсная
характеристика согласованного фильтра будет равна входному сигналу, и при этом
получаем на выходе согласованного фильтра максимальное отношение "сигнал-шум".
При нашем входном сигнале для построения такого фильтра необходимо сначала
создать звено формирования одного трапецеидального импульса схема, которого
изображена на (рис.9).
Рис. 10. Звено формирования радиоимпульса с заданной
огибающей.
На вход звена формирования
радиоимпульса с заданной огибающей (см. рис.9), подаётся сигнал огибающей
радиосигнала (в нашем случае трапеция).
В колебательном звене
формируется гармонический сигнал с несущей частотой wо (в нашем случае 1,11МГц), поэтому на выходе этого звена имеем
гармонический сигнал с частотой wо.
С выхода колебательного звена
сигнал подаётся на сумматор и на звено линии задержки сигнала на Ti (в нашем
случае Ti =15 мкс), а с выхода звена задержки сигнал подаётся на фазовращатель
(он нужен для того чтобы после окончания импульса отсутствовал радиосигнал на
выходе сумматора).
После фазовращателя сигнал тоже
подаётся на сумматор. На выходе сумматора, наконец, имеем трапецеидальные
радиоимпульсы с частотой радиозаполнения wо
т.е. сигнал g (t).
Поскольку нам необходимо получить когерентную пачку из 9 трапецеидальных
видеоимпульсов то необходимо сигнал g (t) подать на звено формирования такой
пачки схема, которой имеет вид как на (рис 10):
Рис. 11. Звено формирования когерентной пачки.
На вход звена формирования
когерентной пачки подаётся сигнал g (t), который представляет собой
трапецеидальный радиоимпульс (или последовательность трапецеидальных
радиоимпульсов).
Далее сигнал идёт на сумматор и
на блок задержки, в котором реализуется задержка входного сигнала на период
следования импульсов в пачке Tip умноженный на номер импульса минус
единица, т.е. (N-1), а с выхода бока задержки снова на сумматор.
Таким образом, на выходе звена
формирования когерентной пачки (т.е. на выходе сумматора) имеем прямоугольную
когерентную пачку трапецеидальных радиоимпульсов, что и требовалось реализовать.
В ходе работы были проведены
соответствующие расчеты и построены графики по ним можно судить о сложности
обработки сигналов. Для упрощения математический расчет проводился пакетах MathCAD 7.0 и MathCAD 8.0. Данная
работа является необходимой частью учебного курса, чтобы студенты имели
представления об особенностях применении различных импульсных радиосигналов в
радиолокации, радионавигации и радио телеметрии, а также могли спроектировать
оптимальный фильтр тем самым, внеся свой скромный вклад в “борьбе" за
информацию.
wо - частота радиозаполнения;
w - частота
Т, (t) - временной сдвиг;
Тi - длительность
радиоимпульса;
Tip - период
следования радиоимпульсов в пачке;
N - число
радиоимпульсов в пачке;
t - время;
1.
Баскаков С.И. "Радиотехнические
цепи и сигналы: Учебник для вузов по спец. "Радиотехника"".
- 2-е изд., перераб. и доп. - М.: Высш. шк., 1988 - 448 с.: ил.
2.
"АНАЛИЗ РАДИОСИГНАЛОВ И РАСЧЁТ ХАРАКТЕРИСТИК ОПТИМАЛЬНЫХ
СОГЛАСОВАННЫХ ФИЛЬТРОВ: Методические указания к курсовой работе по курсу "Теория
радиотехнических сигналов и цепей""/ Киберниченко В.Г., Дороинский Л.Г.,
Свердловск: УПИ 1992.40 с.
3.
"Усилительные устройства": Учеб: пособие для вузов. - М.: Радио
и связь, 1989. - 400 с.: ил.
4.
Букингем М. "Шумы в электронных приборах и системах"/ Пер. с
англ. - М.: Мир, 1986
|