Дипломная работа: Регресійний аналіз інтервальних даних
Дипломная работа: Регресійний аналіз інтервальних даних
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ДНІПРОПЕТРОВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
ДИПЛОМНА РОБОТА
Регресійний
аналіз інтервальних даних
Виконала:
студентка групи МС-03-1
Припутень
Ю.А.
Дніпропетровськ
2008
Реферат
Об’єкт дослідження: алгоритми регресійного
аналізу пристосовані для обробки інтервальних даних.
Мета роботи: розробити програму, яка здійснює знаходження
інтервалів для коефіцієнтів регресії. Програма повинна дозволяти подавати
результати у вигляді зручному для користувачів, мати інтерфейс та бути зручною
у користуванні.
Одержані висновки та їх новизна: в роботі був створений
алгоритм для знаходження інтервальних оцінок коефіцієнтів та розроблено програмне
середовище, що дозволяє досліджувати роботу цього алгоритму.
Результати дослідження можуть бути застосовані для обробки
статистичної інформації.
Перелік ключових слів: лінійна регресія, метод
найменших квадратів, інтервальні дані.
Зміст
Вступ
Розділ
І. Лінійна багатовимірна регресія
Розділ
ІІ.
Довірчі
інтервали регресії. Похибка прогнозу
Розділ
ІІІ. Лінійний регресійний аналіз інтервальних даних
3.1
Метод найменших квадратів для інтервальних даних
3.2
Метод найменших квадратів для лінійної моделі
3.3
Парна регресія
Розділ
IV. Програмний продукт «Інтервальне значення параметрів»
4.1 Текст
програми
4.2
Опис програми
4.3 Результати
роботи програми
Висновки
Список
використаних джерел
Вступ
Перспективний і швидко прогресуючий напрямок останніх років –
математична статистика інтервальних даних. Мова йде про розвиток методів
математичної статистики в ситуації, коли статистичні дані - не числа, а
інтервали, породжені накладенням помилок виміру на значення випадкових величин.
Дана дипломна робота складається з чотирьох розділів. Перші
три розділі мають реферативний характер. В першому розділі викладені деякі
поняття класичної теорії регресійного аналізу. В другому розділі розглянуті
довірчі інтервали для коефіцієнтів регресії. В третьому розділі наведені ідеї і
підходи лінійного регресійного аналізу інтервальніх даних. В четвертому розділі
викладені результати дипломної роботи. Тут наведено алгоритм, текст та опис розроблених
програм, які здійснюють знаходження нотни та оцінок коефіцієнтів регресії в класичному
вигляді та в інтервальних даних.
За допомогою розроблених програм в цьому ж розділі наведено
результати експериментального дослідження залежності величин інтервалів, які
накривають коефіцієнти регресії в залежності від об’єму вибірки та величин
інтервалів в яких знаходяться значення координат вибірки.
Програми створені за допомогою
середовища Maple, так як воно по всім параметрам (швидкість, надійність,
простота у використанні) підходить для написання цих програм.
Постановка задачі. В роботі
необхідно розв’язати такі задачі:
1. Розробити програму.
Програма повинна працювати з вибірками довільної вимірності і довільними
векторами найбільших похибок для кожної координати.
2. Провести чисельно
дослідження залежності верхньої та нижньої меж інтервалів, що накривають
коефіцієнти регресії, в залежності від об’єму вибірки і векторів найбільших
похибок для кожної координати.
Розділ І. Лінійна багатовимірна регресія
Нехай 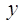 - деяка випадкова величина,
флуктує навколо деякого невідомого значення параметра - деяка випадкова величина,
флуктує навколо деякого невідомого значення параметра 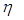 , тобто , тобто 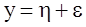 , де , де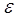 - флуктуація або похибка.
Наприклад, похибка - флуктуація або похибка.
Наприклад, похибка 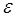 може бути властива самому
експерименту, або похибка може виникати при вимірювані невідомого параметра може бути властива самому
експерименту, або похибка може виникати при вимірювані невідомого параметра 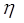 . .
Припустимо тепер, що 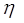 можна представити у вигляді можна представити у вигляді
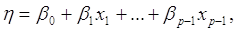
де 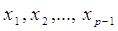 - відомі постійні величини, а - відомі постійні величини, а 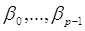 – невідомі
параметри, які потрібно оцінити. – невідомі
параметри, які потрібно оцінити.
Якщо величина 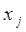 змінюється і при цьому змінна змінюється і при цьому змінна 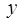 набуває значень набуває значень
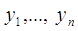 , тобто
можна записати , тобто
можна записати
 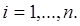 (1.1) (1.1)
У матричному вигляді, отримаємо:
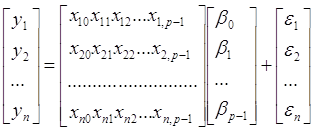
Або
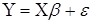 (1.2) (1.2)
де 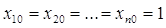 . .
Означення: Матриця 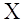 розміру розміру  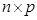 називається регресійною матрицею.
При цьому її елементи називається регресійною матрицею.
При цьому її елементи 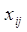 обираються таким чином, щоб обираються таким чином, щоб 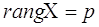 , тобто число
лінійних незалежних стовпців дорівнювало , тобто число
лінійних незалежних стовпців дорівнювало 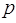 , також матрицю , також матрицю 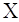 називають матрицею
повного рангу. називають матрицею
повного рангу.
Але в деяких випадках 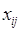 приймає лише два значення 0, 1,
тоді можливі випадки коли в матриці приймає лише два значення 0, 1,
тоді можливі випадки коли в матриці 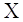 деякі рядки або стовпці
збігаються, тобто є лінійно – залежними. В цьому випадку деякі рядки або стовпці
збігаються, тобто є лінійно – залежними. В цьому випадку 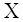 називають матрицею
плану. Змінні називають матрицею
плану. Змінні 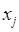 називають регресорами (j=1,…,p-1),
або предикторними змінними, а називають регресорами (j=1,…,p-1),
або предикторними змінними, а 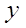 - називають відкликом. - називають відкликом.
Модель (1) або (2) лінійна відносно невідомих параметрів.
Тому її називають лінійною моделлю.
Перед тим як оцінювати вектор 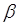 , замітимо, що вся теорія
будується для моделі (2). , замітимо, що вся теорія
будується для моделі (2).
Для оцінки невідомих параметрів 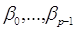 використовують метод найменших
квадратів (МНК), який полягає в мінімізації суми квадратів залишків. Необхідно
мінімізувати величину: використовують метод найменших
квадратів (МНК), який полягає в мінімізації суми квадратів залишків. Необхідно
мінімізувати величину:
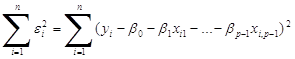 (1.3) (1.3)
за параметрами 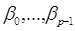 . Вираз (1.3) запишеться так: . Вираз (1.3) запишеться так:
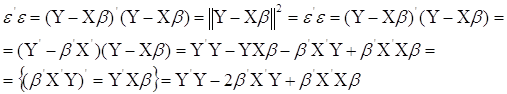 (1.4) (1.4)
Шукаємо градієнт 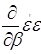 : :
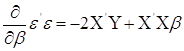
Розв’язуємо рівняння:
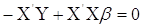
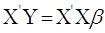
Таким чином
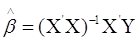 (1.5) (1.5)
Необхідно перевірити, що знайдена стаціонарна точка є точкою мінімуму
функції 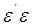 .
Справедлива така тотожність .
Справедлива така тотожність
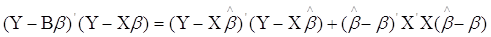
Перевіримо цю рівність:
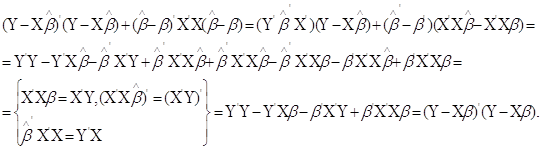
Ліва частина тотожності мінімальна якщо 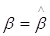 . .
Регресію будемо позначати 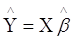 . .
Залишок
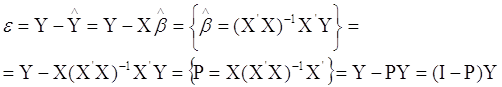
Мінімальне значення суми квадратів залишків 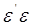 називають залишковою
сумою квадратів (RSS). називають залишковою
сумою квадратів (RSS).
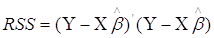
Застосуємо формулу (2.1), RSS перепишеться:
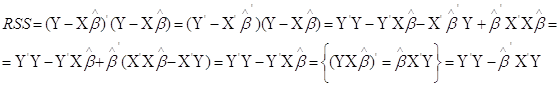
Якщо застосувати формулу (2.2), отримаємо:
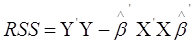 . .
Оцінки 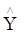 та та 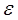 єдині. єдині.
Розділ ІІ. Довірчі інтервали регресії. Похибка прогнозу
Нехай прогнозоване значення 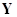 визначається по рівнянню регресії
з оціненими параметрами визначається по рівнянню регресії
з оціненими параметрами
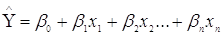 (2.1) (2.1)
В силу того, що 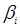 - незміщені оцінки деяких
невідомих параметрів відповідного взаємозв'язку, - незміщені оцінки деяких
невідомих параметрів відповідного взаємозв'язку, 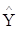 - одне з можливих значень
прогнозованої величини при заданих значеннях - одне з можливих значень
прогнозованої величини при заданих значеннях 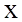 , точніше - це оцінка середнього
значення , точніше - це оцінка середнього
значення 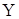 .
Оскільки .
Оскільки 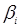 випадкова
величина, то і оцінка випадкова
величина, то і оцінка 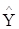 також випадкова і має дисперсію.
Визначимо її значення. також випадкова і має дисперсію.
Визначимо її значення.
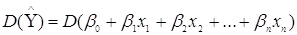
Використавши теорему про дисперсії суми залежних величин,
одержимо:
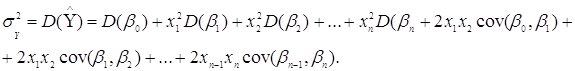
Перепишемо у вигляді:
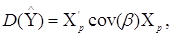
де 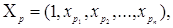 - вектор заданих значень
незалежних змінних. Звідки одержимо: - вектор заданих значень
незалежних змінних. Звідки одержимо:
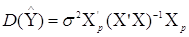
Оскільки значення  нам відомо, то введемо в останню
формулу її оцінку нам відомо, то введемо в останню
формулу її оцінку 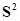 , звідки дисперсія , звідки дисперсія 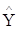 буде: буде:
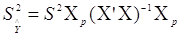 (2.2) (2.2)
Таким чином, середнє значення 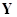 лежить у межах: лежить у межах:
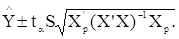 (2.3) (2.3)
Розділ ІІІ. Лінійний регресійний аналіз інтервальних даних
Перейдемо до багатомірного статистичного аналізу. Спочатку з
позиції асимптотичної математичної статистики інтервальних даних розглянемо
оцінки методу найменших квадратів (МНК).
Статистичне дослідження залежностей - одне з найбільш
важливих задач, які виникають у різних галузях науки й техніки. Під словами
"дослідження залежностей" мається на увазі виявлення і опис існуючого
зв'язку між досліджуваними змінами на підставі результатів статистичних
спостережень.
Якщо яка-небудь група об'єктів характеризується змінними 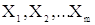 і проведений
експеримент, що складається з n досвідів, де в кожному досвіді ці змінні
вимірюються один раз,то експериментатор одержує набір чисел: і проведений
експеримент, що складається з n досвідів, де в кожному досвіді ці змінні
вимірюються один раз,то експериментатор одержує набір чисел: 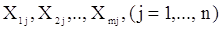 . .
Але процес виміру не дає однозначний результат. Реально
результатом виміру якої-небудь величини Х є два числа: 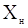 - нижня границя і - нижня границя і 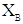 - верхня границя.
Причому - верхня границя.
Причому 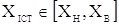 ,
де ,
де 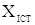 -
істинне значення вимірюваної величини. Результат виміру можна записати як -
істинне значення вимірюваної величини. Результат виміру можна записати як 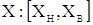 . Інтервальне
число X може бути представлене іншим способом, а саме, . Інтервальне
число X може бути представлене іншим способом, а саме, 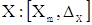 , де , де 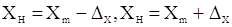 . Тут . Тут 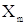 - центр інтервалу (як правило не співпадає
з - центр інтервалу (як правило не співпадає
з 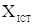 ), а
Δx - максимально можлива похибка виміру. ), а
Δx - максимально можлива похибка виміру.
3.1 Метод найменших квадратів для інтервальних даних
Нехай математична модель задана:
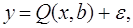 (3.1.1) (3.1.1)
де х = (х1, х2,..., хm)
- вектор впливаючих змінних, що піддаються виміру; 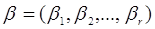 - вектор оцінюваних параметрів
моделі; у - відгук моделі (скаляр); Q(x, - вектор оцінюваних параметрів
моделі; у - відгук моделі (скаляр); Q(x,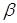 )- скалярна функція векторів х
і )- скалярна функція векторів х
і 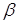 ; і ε
- випадкова похибка. ; і ε
- випадкова похибка.
Нехай проведено n досвідів, причому в кожному досвіді
обмірювані (один раз) значення відгуку (у) і вектора факторів (х).
Результати вимірів можуть бути представлені в наступному виді:
 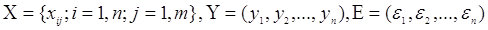
де Х - матриця значень обмірюваного вектора (х) в n
досвідах; Y - вектор значень обмірюваного відгуку в n досвідах; Е - вектор
випадкових помилок. Тоді виконується матричне співвідношення:
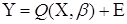 , (3.1.2) , (3.1.2)
де 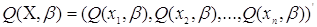 , причому , причому 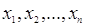 - n-мірні вектора, які становлять
матрицю - n-мірні вектора, які становлять
матрицю 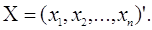
Введемо міру близькості 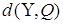 між векторами між векторами 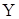 і і 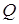 . В МНК в якості . В МНК в якості 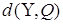 береться
квадратична форма зважених квадратів береться
квадратична форма зважених квадратів 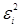 нев'язань нев'язань
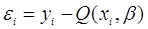 , ,
тобто
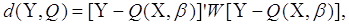
де 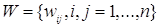 - матриця ваг, що не залежить від - матриця ваг, що не залежить від
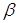 . Тоді як оцінка . Тоді як оцінка
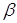 можна
вибрати таке можна
вибрати таке 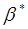 , при якому міра близькості d(Y,Q)
приймає мінімальне значення, тобто , при якому міра близькості d(Y,Q)
приймає мінімальне значення, тобто
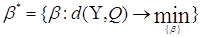 . .
У загальному випадку рішення цього екстремального завдання
може бути не єдиним. Тому надалі будемо мати на увазі одне із цих рішень. Воно
може бути виражене у вигляді:
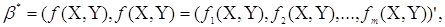
причому 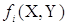 неперервні і дифференційовні по (Х,Y) неперервні і дифференційовні по (Х,Y)
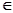 Z,
де Z - область визначення функції f(X,Y). Ці властивості функції f(X,Y)
дають можливість використати підходи статистики інтервальних даних. Z,
де Z - область визначення функції f(X,Y). Ці властивості функції f(X,Y)
дають можливість використати підходи статистики інтервальних даних.
Перевага методу найменших квадратів полягає в порівняльній
простоті й універсальності обчислювальних процедур. Однак не завжди оцінка МНК
є самостійною, що обмежує його застосування на практиці.
Важливим частковим випадком є лінійний МНК, коли Q(x,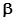 ) є лінійна
функція від ) є лінійна
функція від 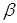 : :
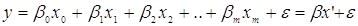 , ,
де 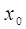 = 1, а = 1, а 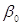 - вільний член лінійної
комбінації. Як відомо, у цьому випадку МНК-оцінка має вигляд: - вільний член лінійної
комбінації. Як відомо, у цьому випадку МНК-оцінка має вигляд:
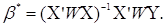
Якщо матриця 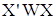 невироджена, то ця оцінка
є єдиною. Якщо матриця ваг W одинична, то невироджена, то ця оцінка
є єдиною. Якщо матриця ваг W одинична, то
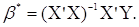
Нехай виконуються наступні припущення щодо розподілу похибок 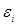 : :
- помилки 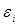 мають нульові
математичні очікування М{ мають нульові
математичні очікування М{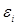 } = 0, } = 0,
- результати спостережень мають однакову дисперсію D {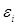 } = } = 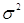 , ,
- помилки спостережень некорельовані, тобто 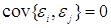 . .
Тоді, як відомо, оцінки МНК є найкращими лінійними оцінками,
тобто спроможними і незміщеними оцінками, які являють собою лінійні функції
результатів спостережень і мають мінімальні дисперсії серед безлічі всіх
лінійних незміщених оцінок. Далі саме цей найбільше практично важливий окремий
випадок розглянемо більш докладно.
Запишемо істині дані в наступній формі:
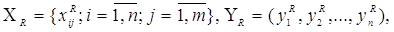
де R - індекс, що вказує на те, що значення істинне.
Істині і обмірювані дані пов’язані таким чином:
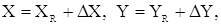
де 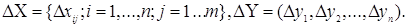
Припустимо, що похибки виміру відповідають граничним умовам
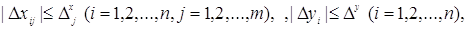 (3.1.3) (3.1.3)
Нехай безліч W можливих значень 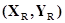 входить в Z - область
визначення функції f(X,Y). Розглянемо входить в Z - область
визначення функції f(X,Y). Розглянемо 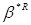 - оцінку МНК, розраховану за
істинним значенням факторів і відгуку, і - оцінку МНК, розраховану за
істинним значенням факторів і відгуку, і 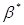 - оцінку МНК, знайдену за відхиленими
похибкам даних. - оцінку МНК, знайдену за відхиленими
похибкам даних.
Тоді
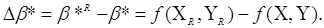
Введемо поняття нотни.
Означення: Величину максимально можливого (по абсолютній
величині) відхилення, викликаного похибками спостережень 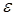 , відомого статистику
значення f(y) від істинного значення f(x), тобто , відомого статистику
значення f(y) від істинного значення f(x), тобто
Nf(x) = sup | f(y) - f(x) |,
де супремум береться по безлічі можливих значень вектора
похибки 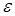 ,
будемо називати нотною. ,
будемо називати нотною.
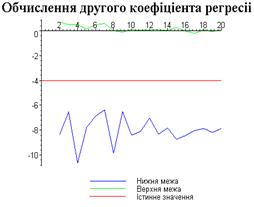
Якщо функція f має частинні похідні другого порядку, а
обмеження на похибку мають вигляд
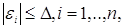 (3.1.4) (3.1.4)
причому 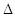 мало, то збільшення функції f
з точністю до нескінченно малих більш високого порядку описується головним
лінійним членом, тобто мало, то збільшення функції f
з точністю до нескінченно малих більш високого порядку описується головним
лінійним членом, тобто
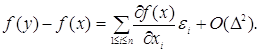
Щоб одержати асимптотичний (при 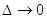 ) вираз для нотни, досить знайти
максимум і мінімум лінійної функції (головного лінійного члена) на кубі,
заданому нерівностями (4.1.4). Легко бачити, що максимум досягається, якщо
покласти ) вираз для нотни, досить знайти
максимум і мінімум лінійної функції (головного лінійного члена) на кубі,
заданому нерівностями (4.1.4). Легко бачити, що максимум досягається, якщо
покласти
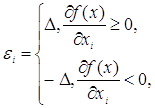
а мінімум, що відрізняється від максимуму тільки знаком,
досягається при 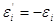 . Отже, нотна з точністю до
нескінченно малих більше високого . Отже, нотна з точністю до
нескінченно малих більше високого
порядку має вигляд
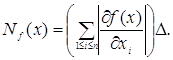 (3.1.5) (3.1.5)
Цей вираз назвемо асимптотичною нотною.
Покладемо:
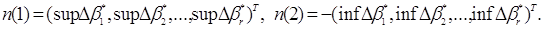
Будемо називати n(1) нижньою нотною, а n(2) верхньою
нотною.
Припустимо, що при безмежному зростанні числа вимірів n,
тобто при
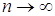 вектора n(1), n(2) прямують до
постійних значень вектора n(1), n(2) прямують до
постійних значень 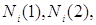 відповідно. Тоді відповідно. Тоді 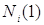 будемо називати нижньою
асимптотичною нотною, а будемо називати нижньою
асимптотичною нотною, а 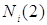 - верхньою асимптотичною нотною. - верхньою асимптотичною нотною.
Розглянемо довірчу множину 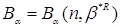 для вектора параметрів для вектора параметрів 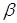 , тобто
замкнута зв'язна множина точок в r-мірному евклідовому просторі така, що , тобто
замкнута зв'язна множина точок в r-мірному евклідовому просторі така, що 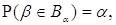 де α
- довірча ймовірність, що відповідає Bα (α ≈
1). Інакше кажучи, де α
- довірча ймовірність, що відповідає Bα (α ≈
1). Інакше кажучи, 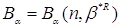 є область розсіювання випадкового
вектора є область розсіювання випадкового
вектора 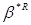 з
довірчою ймовірністю α і числом досвідів n. з
довірчою ймовірністю α і числом досвідів n.
З визначення верхньої й нижньої нотни треба, щоб завжди
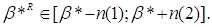
Відповідно до визначення нижньої асимптотичної нотни й
верхньої асимптотичної нотни можна вважати, що 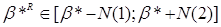 при досить великій кількості
спостережень n. Цей багатомірний інтервал описує r-мірний гіперпаралелепіпед P. при досить великій кількості
спостережень n. Цей багатомірний інтервал описує r-мірний гіперпаралелепіпед P.
Розіб'ємо P на L гіперпаралелепіпедів. Нехай 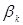 - внутрішня точка k-го
гіперпаралелепіпеда. З огляду на властивості довірчої множини і спрямовуючи L
до нескінченності, можна стверджувати, що - внутрішня точка k-го
гіперпаралелепіпеда. З огляду на властивості довірчої множини і спрямовуючи L
до нескінченності, можна стверджувати, що
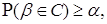
де 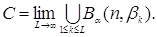
Таким чином, безліч C характеризує невизначеність при
оцінюванні вектора 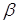 . Його можна назвати
довірчою множиною в статистиці інтервальних даних. . Його можна назвати
довірчою множиною в статистиці інтервальних даних.
Введемо деяку міру М(X), що характеризує "величину"
множини 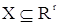 .
По визначенню міри вона задовольняє умові: якщо .
По визначенню міри вона задовольняє умові: якщо
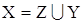 і і 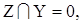 то то 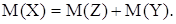
Прикладом такої міри є площа для r = 2 і об’єма для r = 3.
Тоді:
М(C) = М(P) + М(F), (3.1.6)
де F = C \ P. Тут М(F) характеризує міру статистичної
невизначеності, у більшості випадків вона спадає при збільшенні числа досвідів
n. У той же час М(P) характеризує міру інтервальної невизначеності, і, як
правило, М(P) прагне до деякої постійної величини при збільшенні числа досвідів
n. Нехай тепер потрібно знайти те число досвідів, при якому статистична невизначеність
становить δ-ю частина загальної невизначеності, тобто
М(F) = δ М(C), (4.1.7)
де δ < 1. Тоді, підставивши
співвідношення (4.1.7) у рівність (4.1. 6) і вирішивши рівняння відносно n,
одержимо шукане число досвідів. В асимптотичній математичній статистиці інтервальних
даних воно називається "раціональним обсягом вибірки".
3.2 Метод найменших квадратів для лінійної моделі
Розглянемо найбільш важливий для практики окремий випадок
МНК, коли модель є лінійною.
Для простоти опису перетворень пронормуємо змінні хij,уi. Наступним чином:
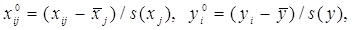
де
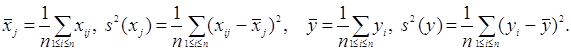
Тоді
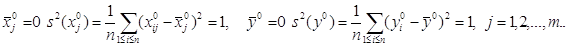
Надалі будемо вважати, що розглянуті змінні пронормовані
описаним образом, і верхні індекси опустимо. Для полегшення демонстрації
основних ідей приймемо досить природні припущення.
1. Для розглянутих змінних існують наступні межі:
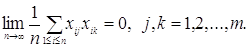
2. Кількість досвідів n таке, що можна користуватися
асимптотичними результатами, отриманими при 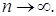
3. Погрішності виміру задовольняють одному з наступних типів
обмежень:
Тип 1. Абсолютні погрішності виміру обмежені згідно (4.1.3):
Тип 2. Відносні погрішності виміру обмежені:
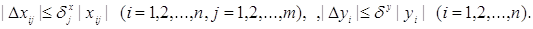
Тип 3. Обмеження накладені на суму погрішностей:
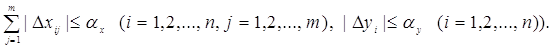
Перейдемо до обчислення нотни оцінки МНК. Справедлива
рівність:
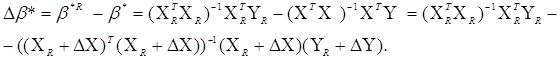
Скористаємося наступною теоремою з теорії матриць.
Теорема. Якщо функція f(λ) розкладається в степеневий
ряд у колі збіжності |λ – λ0| < r, тобто
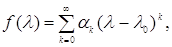
то це розкладання зберігає силу, якщо скалярний аргумент
замінити будь-якою матрицею А, характеристичні числа якої λk,
k = 1,…,n, лежать всередині кола збіжності.
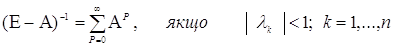
Легко переконатися, що:
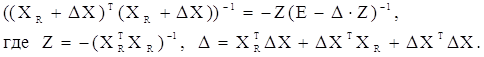
Це випливає з послідовності рівностей:
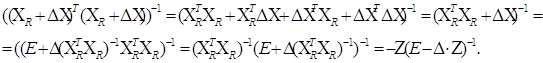
Застосуємо наведену вище теорему з теорії матриць, припускаючи
А = Δ Z і приймаючи, що власні числа цієї матриці
задовольняють нерівності |λk|<1. Тоді одержимо:
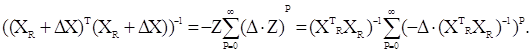
Підставивши останнє співвідношення на закінчення згаданої
теореми, одержимо:
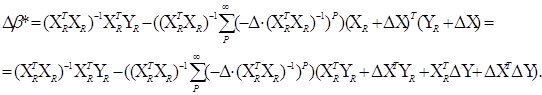
Для подальшого аналізу знадобиться допоміжне твердження.
Виходячи із припущень 1-3, доведемо, що:
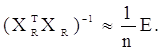
Доведення. Справедлива рівність
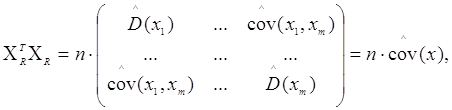
де 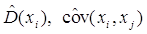 - спроможні і незміщені оцінки
дисперсій і коефіцієнтів коваріації, тобто - спроможні і незміщені оцінки
дисперсій і коефіцієнтів коваріації, тобто
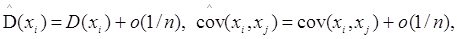
тоді
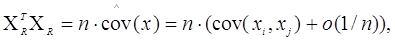
де 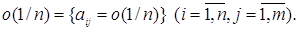
Інакше кажучи, кожен елемент матриці, позначеної як о(1/n), є
нескінченно малою величиною порядку 1/n. Для розглянутого випадку cov(x)
= E, тому
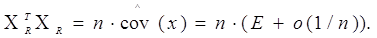
Припустимо, що n досить велике і можна вважати, що власні
числа матриці о(1/n) менше одиниці по модулю, тоді
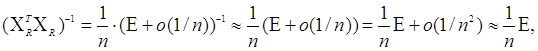
що і було потрібно довести.
Підставимо доведене асимптотичне співвідношення у формулу для
приросту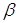 *,одержимо *,одержимо
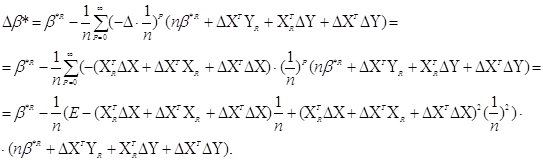
Виразимо Δ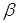 * відносно приросту ΔХ,
ΔY до 2-гo порядку * відносно приросту ΔХ,
ΔY до 2-гo порядку
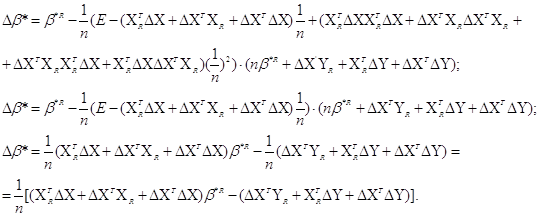
Перейдемо від матричної до скалярної форми, опускаючи індекс
(R):
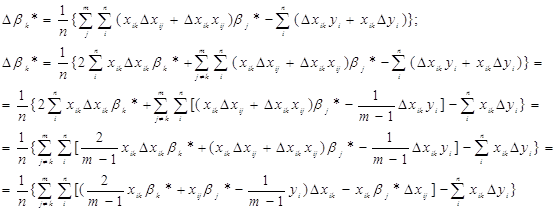
Будемо шукати max(|Δ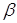 k*|) по Δxij
і Δyi (i=1,…, п;j=1,…, m). Для цього розглянемо всі три
раніше введених типи обмежень на похибки виміру. k*|) по Δxij
і Δyi (i=1,…, п;j=1,…, m). Для цього розглянемо всі три
раніше введених типи обмежень на похибки виміру.
Тип 1 (абсолютні похибки виміру обмежені). Тоді:
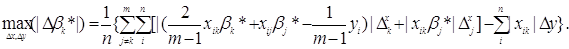
Тип 2 (відносні похибки виміру обмежені). Аналогічно
одержимо:
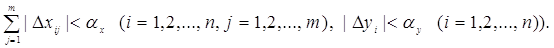
Тип З (обмеження накладені на суму похибок). Припустимо, що |Δ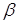 k*| досягає
максимального значення при таких значеннях погрішностей Δxij
і Δyi, k*| досягає
максимального значення при таких значеннях погрішностей Δxij
і Δyi,
які ми позначимо як:
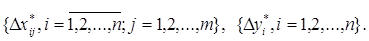
тоді:
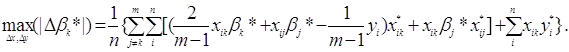
Через лінійність останнього вираження і виконання обмеження
типу 3:
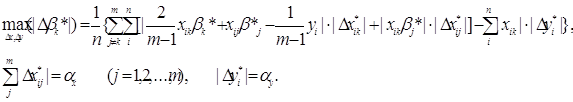
Для спрощення запису зробимо наступні заміни:
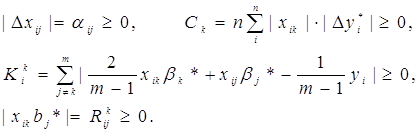
Тепер для досягнення поставленої мети можна сформулювати
наступне завдання, що розділяється на m типових завдань оптимізації:
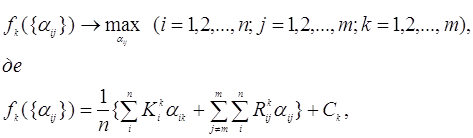
при обмеженнях
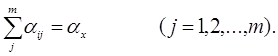
Перепишемо функції, що мінімізуємо, в наступному вигляді:
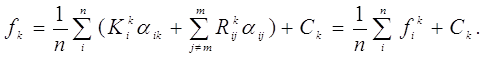
Очевидно, що fik > 0.
Легко бачити, що
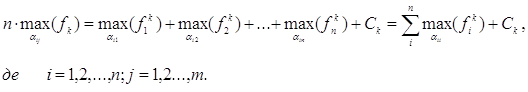
Отже, необхідно вирішити nm завдань
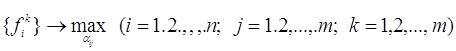
при обмеженнях "типу рівності":
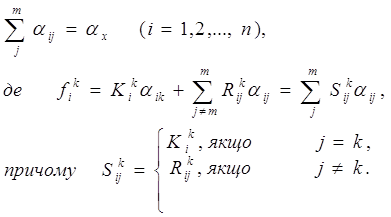
Сформульоване завдання пошуку екстремуму функції. Воно легко
вирішується. Оскільки
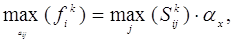
то максимальне відхилення МНК - оцінки k-ого параметра
дорівнює
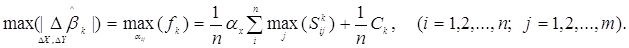
3.3 Парна регресія
Найбільш простий і одночасно найбільше широко застосовуваний
окремий випадок парної регресії розглянемо докладніше. Модель має вигляд
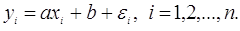 (3.3.1) (3.3.1)
Тут xi - значення фактора (незалежної
змінної), 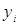 -
значення відгуку (залежної змінної), -
значення відгуку (залежної змінної), 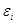 - статистичні похибки, - статистичні похибки, 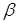 - невідомі параметри,
оцінювані методом найменших квадратів. Модель (3.3.1) може бути записана у
вигляді: - невідомі параметри,
оцінювані методом найменших квадратів. Модель (3.3.1) може бути записана у
вигляді:
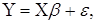 (3.3.2) (3.3.2)
якщо покласти
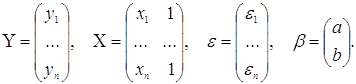
Природно прийняти, що похибки факторів описуються матрицею
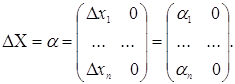
У розглянутій моделі інтервального методу найменших квадратів
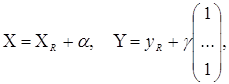
де X, 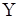 - спостережувані значення фактора
і відгуку, XR, yR - істині значення змінних, - спостережувані значення фактора
і відгуку, XR, yR - істині значення змінних, 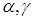 - погрішності
вимірів змінних. Нехай - погрішності
вимірів змінних. Нехай 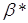 - оцінка методу найменших
квадратів, обчислена за спостережуваним значенням змінних, - оцінка методу найменших
квадратів, обчислена за спостережуваним значенням змінних, 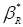 - аналогічна оцінка,
знайдена за істинним значенням. Відповідно до раніше проведених міркувань - аналогічна оцінка,
знайдена за істинним значенням. Відповідно до раніше проведених міркувань
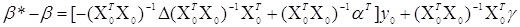 (3.3.3) (3.3.3)
з точністю до нескінченно малих більш високого порядку по 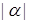 і і 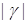 . У формулі (3.3.3)
використане позначення . У формулі (3.3.3)
використане позначення 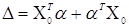 . Обчислимо праву частину в (3.3.3),
виділимо головний лінійний член і знайдемо нотну. . Обчислимо праву частину в (3.3.3),
виділимо головний лінійний член і знайдемо нотну.
Легко бачити, що
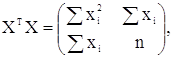 (3.3.4) (3.3.4)
де підсумовування проводиться від 1 до n. Для спрощення
позначень надалі і до кінця дійсного пункту не будемо вказувати ці межі
підсумовування. З (3.3.4) випливає, що
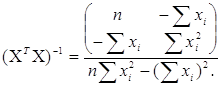 (3.3.5) (3.3.5)
Легко підрахувати, що
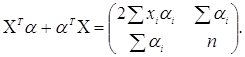 (3.3.6) (3.3.6)
Покладемо
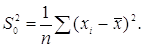
Тоді знаменник в (3.3.5) дорівнює 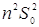 . З (3.3.5) і (3.3.6) випливає, що . З (3.3.5) і (3.3.6) випливає, що
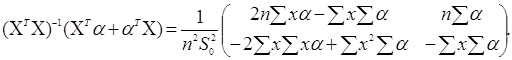 (3.3.7) (3.3.7)
Тут і далі опустимо індекс і, по якому проводиться
підсумовування. З (3.3.5) і (3.3.7) випливає:
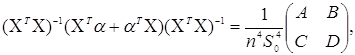 (3.3.8) (3.3.8)
де
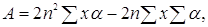
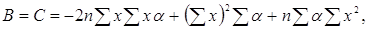
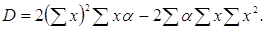
Обчислимо основний множник в (3.3.3)
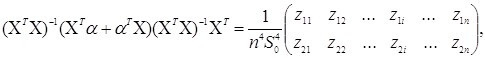 (3.3.9) (3.3.9)
де
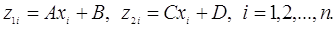
Перейдемо до обчислення другого члена з 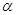 в (3.3.3). Маємо в (3.3.3). Маємо
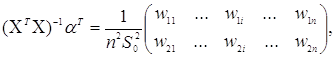 (3.3.10) (3.3.10)
де
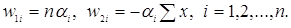
Складаючи праві частини (3.3.9) і (3.3.10) і помножуючи на у,
одержимо остаточний вид члена з 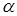 в (3.3.3): в (3.3.3):
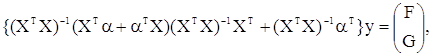 (3.3.11) (3.3.11)
де
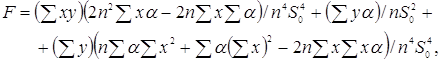
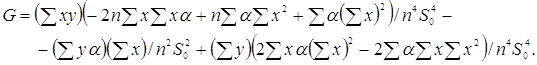
Для обчислення нотни виділимо головний лінійний член.
Спочатку знайдемо частинні похідні. Маємо
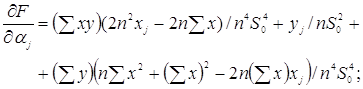 (3.3.12) (3.3.12)
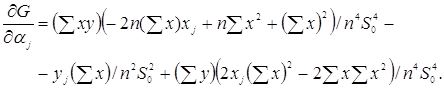
Якщо обмеження мають вигляд
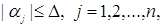
то максимально можливе відхилення оцінки а* параметра а
через погрішності 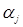 таке: таке:
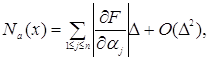 (3.3.13) (3.3.13)
де похідні задані формулою (3.3.12).
Розділ IV. Програмний продукт «Інтервальне значення
параметрів»
4.1 Текст програми
restart:with(LinearAlgebra):
Klassic ocenki_parametrov:
> ocenki_parametrov:=proc(viborka,nomer_zavis_koord)
local kol_strok,kol_stolbcov,matrica_X,vektor_Y_1,vektor_Y,
X_transpon,otvet_prom,otvet;
kol_strok:=RowDimension(viborka):
kol_stolbcov:=ColumnDimension(viborka):
matrica_X:=DeleteColumn(viborka,nomer_zavis_koord..nomer_zavis_koord):
vektor_Y_1:=DeleteColumn(viborka,1..nomer_zavis_koord-1):
vektor_Y:=DeleteColumn(vektor_Y_1,2..kol_stolbcov-nomer_zavis_koord+1):
X_transpon:=Transpose(matrica_X):
otvet_prom:=MatrixInverse(MatrixMatrixMultiply(X_transpon,matrica_X)):
otvet:=MatrixMatrixMultiply(MatrixMatrixMultiply(otvet_prom,X_transpon),vektor_Y):
end proc:
Notna ocenki_parametrov:
> notna_ocenki_parametrov:=proc(viborka,nomer_zavis_koord,pogr)
local kol_strok, kol_stolbcov, matrica_X,vektor_Y_1,
vektor_Y,
n,m,j,k,c,i,pogr_Y,pogr_X,vector_beta,pod_sum_vnutr,summa_vnutr,sum_vnesh,pod_summa_2,summa_2,summa;
global otv:
kol_strok:=RowDimension(viborka):
kol_stolbcov:=ColumnDimension(viborka):
matrica_X:=DeleteColumn(viborka,nomer_zavis_koord..nomer_zavis_koord):
vektor_Y_1:=DeleteColumn(viborka,1..nomer_zavis_koord-1):
vektor_Y:=DeleteColumn(vektor_Y_1,2..kol_stolbcov-nomer_zavis_koord+1):
m:=kol_stolbcov-1:
n:=kol_strok:
pod_sum_vnutr:=array(1..n):
summa_vnutr:=array(1..m):
sum_vnesh:=array(1..m):
pod_summa_2:=array(1..n):
summa_2:=array(1..m):
summa:=array(1..m):
pogr_Y:=pogr[nomer_zavis_koord]:
pogr_X:=array(1..m):
for i to m do
if i<nomer_zavis_koord then
pogr_X[i]:=pogr[i]:
else pogr_X[i]:=pogr[i+1]:
end if:
end do:
vector_beta:=ocenki_parametrov(viborka,nomer_zavis_koord):
for k to m do
for j to m do
for i to n do
pod_sum_vnutr[i]:=abs(2*matrica_X[i,k]*vector_beta[k,1]/(m-1)
+matrica_X[i,j]*vector_beta[j,1]-
vektor_Y[i,1]/(m-1))*pogr_X[k] +abs(matrica_X[i,k]*vector_beta[j,1])*pogr_X[j]:
end do:
summa_vnutr[j]:=sum('pod_sum_vnutr[ii]','ii'=1..n):
end do:
sum_vnesh[k]:=sum('summa_vnutr[jj]','jj'=1..k-1)+sum('summa_vnutr[jj]','jj'=k+1..m):
for c to n do
pod_summa_2[c]:=abs(matrica_X[c,k]):
end do:
summa_2[k]:=sum('pod_summa_2[d]','d'=1..n)*pogr_Y:
summa[k]:=(sum_vnesh[k]+summa_2[k])/n:
end do:
otv:=summa:
end proc:
Final
> interval_znachen_param:=proc(viborka,nomer_zavis_koord,pogr)
Local razmer,massiv_interv_koeff,parametric,notna,i:
global interv:
razmer:=ColumnDimension(viborka)-1:
massiv_interv_koeff:=array(1..razmer):
interv:=Matrix(1..razmer,1..2):
parametri:=ocenki_parametrov(viborka,nomer_zavis_koord,pogr):
notna:=notna_ocenki_parametrov(viborka,nomer_zavis_koord,pogr):
for i to razmer do
massiv_interv_koeff[i]:=parametri[i,1]:
interv[i,1]:=massiv_interv_koeff[i]-notna[i]:
interv[i,2]:=massiv_interv_koeff[i]+notna[i]:
end do:
interv:
end proc:
> generator_viborki:=proc(DIGITS,obem_vibork,distrib,parametr)
global VIBORK:
local i:
Digits:=DIGITS:
VIBORK:=array(1..obem_vibork):
if distrib=NORMAL then
for i to obem_vibork do
VIBORK[i]:=stats[random, normald[0,parametr]](1):
end do:
VIBORK:
end if:
end proc:
> real_viborka:=proc(DIGITS,kol_razb,distrib,parametr,model)
global mass_Y,mass_X1,mass_X2:
local oshibki,nom,i,j:
mass_Y:=array(1..(kol_razb+1)^2):
mass_X1:=array(1..(kol_razb+1)^2):
mass_X2:=array(1..(kol_razb+1)^2):
oshibki:=generator_viborki(DIGITS,(kol_razb+1)^2,distrib,parametr):
nom:=0:
for i from 0 to kol_razb do
for j from 0 to kol_razb do
nom:=nom+1:
mass_Y[nom]:=eval(model,{x1=i/kol_razb,x2=j/kol_razb})+oshibki[nom]:
mass_X1[nom]:=evalf(i/kol_razb):
mass_X2[nom]:=evalf(j/kol_razb):
end do:
end do:
mass_Y:
end proc:
> okrug_real_viborka:=proc(DIGITS,digits_okrug,kol_razb,distrib,
parametr,model)
global VIB:
local okrug_mass_Y,okrug_mass_X1,okrug_mass_X2:
Digits:=digits_okrug:
okrug_mass_Y:=array(1..(kol_razb+1)^2):
okrug_mass_X1:=array(1..(kol_razb+1)^2):
okrug_mass_X2:=array(1..(kol_razb+1)^2):
VIB:=Matrix(1..(kol_razb+1)^2,1..3):
okrug_mass_Y:=real_viborka(DIGITS,kol_razb,distrib,parametr,model):
okrug_mass_X1:=mass_X1:
okrug_mass_X2:=mass_X2:
for i to (kol_razb+1)^2 do
VIB[i,1]:=okrug_mass_Y[i]:
VIB[i,2]:=okrug_mass_X1[i]:
VIB[i,3]:=okrug_mass_X2[i]:
end do:
VIB:
end proc:
> with(plots):
grafic_ocenok:=proc(DIGITS,digits_okrug,kol_razb,distrib,parametr,model,pogr,perek)
global ViBVreM,INTERVAL:
local gg1n,gg1v,s, gg2n,gg2v,ggg1n,g1, ggg2n,g2,g21,
ggg2v,g22,ggg1v:
gg1n:=array(2..kol_razb):
gg1v:=array(2..kol_razb):
for s from 2 to kol_razb do
ViBVreM:=okrug_real_viborka(DIGITS,digits_okrug,s,distrib,parametr,model):
INTERVAL:=interval_znachen_param(ViBVreM,1,pogr):
gg1n[s]:=INTERVAL[1,1]:
gg1v[s]:=INTERVAL[1,2]:
gg2n[s]:=INTERVAL[2,1]:
gg2v[s]:=INTERVAL[2,2]:
end do:
ggg1n:=[seq([b,gg1n[b]],b=2..kol_razb)]:
g1:=plot(ggg1n,'colour'='blue',legend="Нижня
межа");
ggg1v:=[seq([b,gg1v[b]],b=2..kol_razb)]:
g2:=plot(ggg1v,'colour'='green',legend="Верхня
межа");
ggg2n:=[seq([b,gg2n[b]],b=2..kol_razb)]:
g21:=plot(ggg2n,'colour'='blue',legend="Нижня
межа");
ggg2v:=[seq([b,gg2v[b]],b=2..kol_razb)]:
g22:=plot(ggg2v,'colour'='green',legend="Верхня
межа");
if perek =1 then
gt:=plot(2,t=0..kol_razb,'colour'='red',legend="Істинне
значення"):
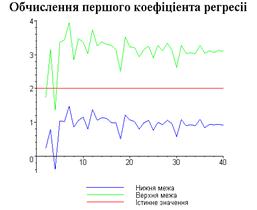
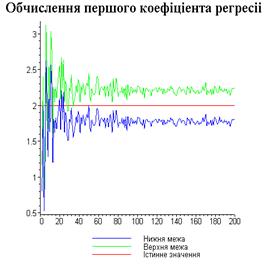
display([g1,g2,gt],'title'="Обчислення першого
коефіціента регресіі",'titlefont'=[TIMES,BOLD,18]):
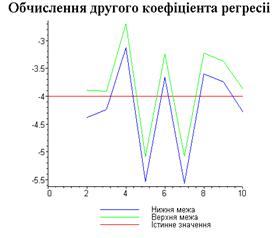
else
gt:=plot(-4,t=0..kol_razb,'colour'='red',legend="Істинне
значення"):
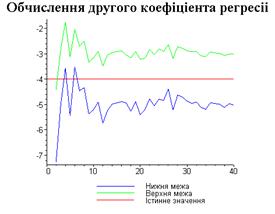
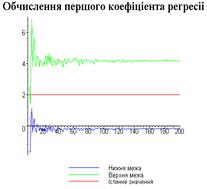
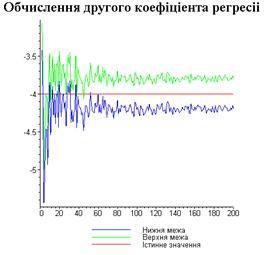
display([g21,g22,gt],'title'="Обчислення другого
коефіціента регресіі",'titlefont'=[TIMES,BOLD,18]):
end if:
end proc:
4.2 Опис програми
Основним результатом дипломної роботи є програмний продукт. В роботі
представлена програма під назвою «Інтервальне значення параметрів», яка
реалізує знаходження інтервалів для коефіцієнтів регресії. Під час роботи ця програма
використовує допоміжні процедури, які обчислюють класичну оцінку коефіцієнтів
регресії та нотну. Програма написана в прикладному математичному пакеті Maple,
який являється одним з самих потужних інтелектуальних систем комп`ютерної алгебри. Результати програми
представлені на графіках.
Програма складається з чотирьох процедур та реалізації
графічного інтерфейсу.
Спочатку відбувається підключення необхідних модулів:
restart;
with(LinearAlgebra):
with(plots):
with(stats):
Надалі розглянемо процедури, які були використані в даній
програмі.
Розглянемо процедуру під назвою ocenki_parametrov. Ця процедура
отримує вхідні дані, які вводить користувач та знаходить оцінки коефіцієнтів
лінійної регресії за допомогою методу найменших квадратів (МНК). В ній оголошені
такі змінні: viborka– це вибірка з якою ми будемо працювати, вона
вводиться з клавіатури користувачем; nomer_zavis_koord –вектор Y.
В процедурі задані локальні змінні, які використовуються у
якомусь невеликому відрізку програми, це може бути невеликий цикл тощо.
В якості локальних змінних оголошенні kol_strok- кількість строк матриці matrica_X
що вводиться
з клавіатури користувачем, kol_stolbcov- кількість
стовпчиків даної матриці, X_transpon- транспонована матриця до
матриці Х, vektor_Y- вектор спостережень, otvet- вектор-стовпчик
оцінок коефіцієнтів, що знаходяться за формулою 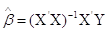 . .
otvet:=MatrixMatrixMultiply(MatrixMatrixMultiply(otvet_prom,X_transpon),vektor_Y):.
Розглянемо процедуру під назвою Notna
ocenki_parametrov. Ця процедура отримує вхідні дані, які вводить
користувач та знаходить нотну. В ній оголошені такі змінні: viborka– це вибірка з
якою ми будемо працювати, вона вводиться з клавіатури користувачем; nomer_zavis_koord
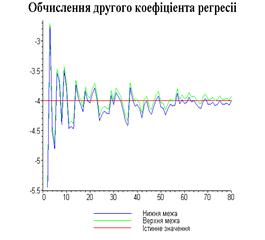
–вектор Y, pogr – це похибка, її користувач визначає самостійно і
вводить з клавіатури.
В процедурі задані локальні та глобальні змінні, локальні
змінні використовуються у якомусь невеликому відрізку програми, це може бути
невеликий цикл тощо, а глобальні змінні фігурують на протязі всієї програми.
В якості локальних змінних оголошені n- кількість
строк матриці Х, m- кількість стовпчиків матриці Х, j,k,c,i –
номер елемента вибірки, kol_strok та kol_stolbcov - розмір матриці Х,
matrica_X що вводиться з клавіатури користувачем, vektor_Y- вектор
спостережень, pogr_Y,pogr_X - це похибки, її користувач визначає
самостійно і вводить з клавіатури, vector_beta - вектор-стовпчик
знайденних оцінок коефіцієнтів в процедурі ocenki_parametrov,
pod_sum_vnutr – значення яке відповідає формулі
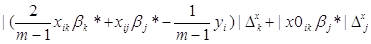 , ,
summa_vnutr - значення яке відповідає формулі
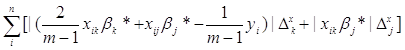 , ,
sum_vnesh - значення яке відповідає формулі
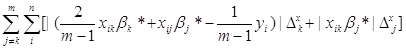 , ,
pod_summa_2 - значення яке відповідає формулі 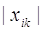 , summa_2 - значення яке
відповідає формулі , summa_2 - значення яке
відповідає формулі
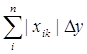 , ,
summa - значення яке відповідає формулі
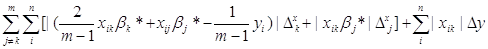 . .
Глобальні змінні otv – значення нотни, знайдене за
формолою
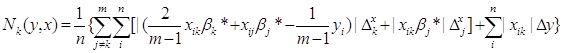
Далі в процедурі формуються масиви для pod_sum_vnutr,
summa_vnutr, sum_vnesh, pod_summa_2, summa_2, summa які використовуються
для подальших обчислень.
pod_sum_vnutr:=array(1..n):
summa_vnutr:=array(1..m):
sum_vnesh:=array(1..m):
pod_summa_2:=array(1..n):
summa_2:=array(1..m):
summa:=array(1..m):
Розмір матриці Х формується за допомогою функцій RowDimension
та ColumnDimension.
kol_strok:=RowDimension(viborka):
kol_stolbcov:=ColumnDimension(viborka):
Так як формула для знаходження нотни є складною, обчислимо її
частинами, щоб спростити дії для машини та не помилитись.
Спочатку рахуємо вираз під внутрішньою сумою.
for i to n do
pod_sum_vnutr[i]:=abs(2*matrica_X[i,k]*vector_beta[k,1]/(m-1)
+matrica_X[i,j]*vector_beta[j,1]-vektor_Y[i,1]/(m-1))*pogr_X[k]
+abs(matrica_X[i,k]*vector_beta[j,1])*pogr_X[j]
end do:
Далі знаходимо значення під внутрішньою сумою.
for j to m do
summa_vnutr[j]:=sum('pod_sum_vnutr[ii]','ii'=1..n):
end do:
Рахуємо зовнішню суму.
for k to m do
sum_vnesh[k]:=sum('summa_vnutr[jj]','jj'=1..k-1)
+sum('summa_vnutr[jj]','jj'=k+1..m):
end do:
Рахуємо другу частину формули.
for c to n do
pod_summa_2[c]:=abs(matrica_X[c,k]):
end do:
summa_2[k]:=sum('pod_summa_2[d]','d'=1..n)*pogr_Y:
summa[k]:=(sum_vnesh[k]+summa_2[k])/n:
Виводимо відповідь: otv:=summa:
Розглянемо процедуру під назвою interval_znachen_param. В цій процедурі,
використовуючи результати попередніх двох процедур ocenki_parametrov та Notna
ocenki_parametrov, рахуються інтервали в яких знаходяться оцінки
коефіцієнтів регресії. В ній оголошені такі змінні: viborka– це вибірка довільного
об’єму та вимірності з якою ми будемо працювати, вона вводиться з клавіатури
користувачем; nomer_zavis_koord –номер координати, яка трактується як
залежна, pogr – вектор максимальних величин похибок, з якими визначенні
координати елементів вибірки.
В процедурі задані локальні та глобальні змінні, локальні
змінні використовуються у якомусь невеликому відрізку програми, це може бути
невеликий цикл тощо, а глобальні змінні фігурують на протязі всієї програми.
В якості локальних змінних оголошені razmer – кількість
стовпців, massiv_interv_koeff, parametric – знайдені оцінки
коефіцієнтів, notna-знайдена нотна, і – номер коефіцієнту
регресії.
Глобальні змінні interv – шуканий інтервал.
Далі в програмі формуються масиви для massiv_interv_koeff,
interv, які використовуються для подальших обчислень.
massiv_interv_koeff:=array(1..razmer):
interv:=Matrix(1..razmer,1..2):
Так як формула для правої та лівої границі інтервалу в методі
інтервальних даних є складною, обчислимо її частинами, щоб спростити дії для
машини та не помилитись.
for i to razmer do
massiv_interv_koeff[i]:=parametri[i,1]:
interv[i,1]:=massiv_interv_koeff[i]-notna[i]:
interv[i,2]:=massiv_interv_koeff[i]+notna[i]:
end do:
Програма повертає значення верхньої та нижньої меж
інтервалів, які накривають коефіцієнти регресії. В результаті роботи цієї
процедури ми отримали результати, обчислені у вигляді зручному для побудови
графіка за цими даними.
Розглянемо процедуру під назвою generator_viborki.
В цій процедурі ми вибираємо вибірку довільного об’єму, значення
якої є нормально розподіленими. В ній оголошені такі змінні: DIGITS – кількість
знаків після коми, obem_vibork- об’єм нашої вибірки, distrib- вибір
розподілу, parametr- коефіцієнти.
В процедурі задані глобальні змінні, що фігурують на протязі
всієї програми.
В якості глобальних змінних оголошені VIBORK- це вибірка з
якою ми будемо працювати.
Далі в програмі формується масив для VIBORK.
VIBORK:=array(1..obem_vibork):
if distrib=NORMAL then
for i to obem_vibork do
VIBORK[i]:=stats[random, normald[0,parametr]](1):
end do:
Таким чином ми отримаємо вибірку.
Розглянемо процедуру під назвою grafic_ocenok. В цій процедурі
за отриманими вище даними будуємо графіки на яких зображені інтервали для
коефіцієнтів регресії. В ній оголошені такі змінні: DIGITS – кількість знаків
після коми, digits_okrug - кількість знаків після коми значень нашої
вибірки, kol_razb - обєм нашої вибірки, distrib – вибір розподілу,
parametr - кількість коефіцієнтів регресії, model – рівняння
регресії, pogr - похибка.
В процедурі задані локальні та глобальні змінні, локальні
змінні використовуються у якомусь невеликому відрізку програми, це може бути
невеликий цикл тощо, а глобальні змінні фігурують на протязі всієї програми.
В якості локальних змінних оголошені gg1n, gg1v, gg2n,gg2v
– нижня і верхня границі інтервалів для кожного коефіцієнту регресії, s -
обєм вибірки.
Глобальні змінні ViBVreM - це округлена вибірка, INTERVAL-
інтервальне значення параметрів.
Далі в програмі формуються масиви для верхніх і нижніх меж
gg1n:=array(2..kol_razb):
gg1v:=array(2..kol_razb):
Задаємо колір нижньої та верхньої меж та істинного значення
для двох коефіцієнтів.
ggg1n:=[seq([b,gg1n[b]],b=2..kol_razb)]:
g1:=plot(ggg1n,'colour'='blue',legend="Нижня
межа");
ggg1v:=[seq([b,gg1v[b]],b=2..kol_razb)]:
g2:=plot(ggg1v,'colour'='green',legend="Верхня
межа");
ggg2n:=[seq([b,gg2n[b]],b=2..kol_razb)]:
g21:=plot(ggg2n,'colour'='blue',legend="Нижня
межа");
ggg2v:=[seq([b,gg2v[b]],b=2..kol_razb)]:
g22:=plot(ggg2v,'colour'='green',legend="Верхня
межа");
gt:=plot(2,t=0..kol_razb,'colour'='red',legend="Істинне
значення"):
gt:=plot(-4,t=0..kol_razb,'colour'='red',legend="Істинне
значення"):
Підписуємо графіки
display([g1,g2,gt],'title'="Обчислення першого
коефіціента регресіі",'titlefont'=[TIMES,BOLD,18]):
display([g21,g22,gt],'title'="Обчислення другого
коефіціента регресіі",'titlefont'=[TIMES,BOLD,18]):
Таким чином результати розробленої програми представлені на
графіках.
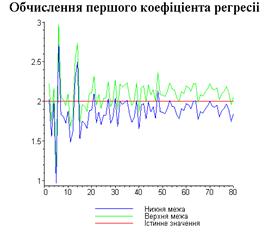
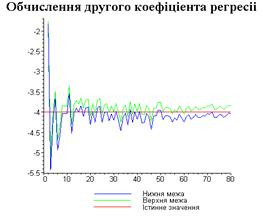
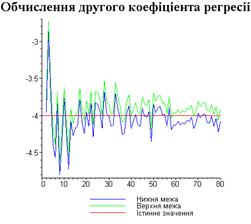
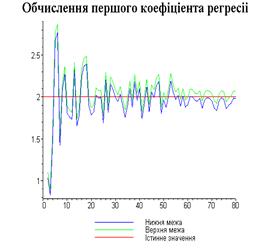
4.3. Результати роботи програми
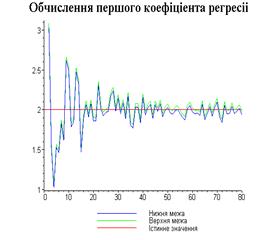
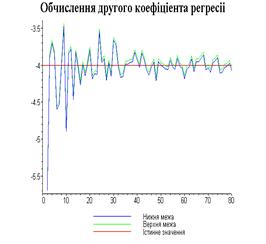
Результати програми для вибірки діапазону 1-80.
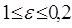
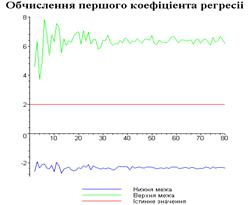 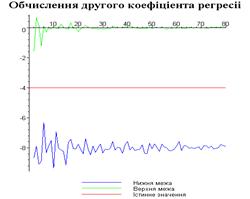
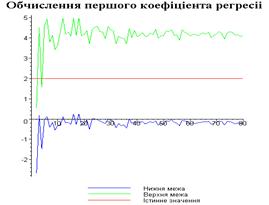 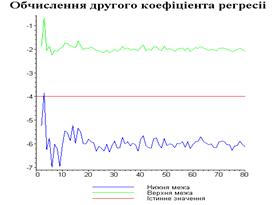
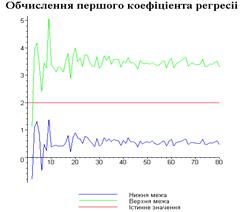 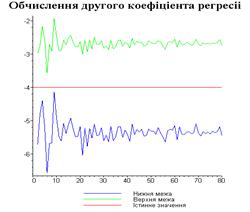
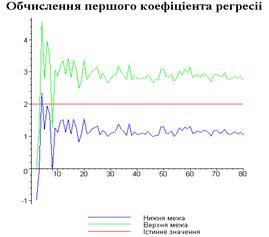 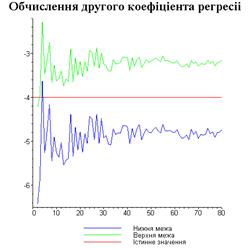
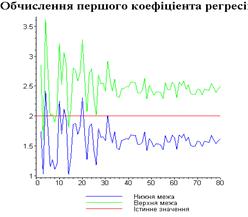 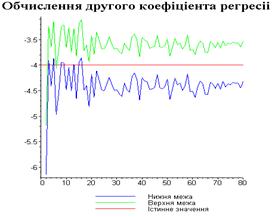
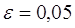
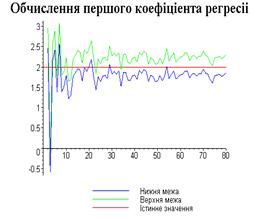 
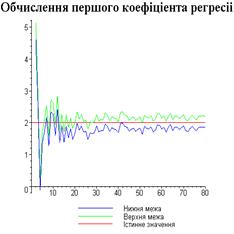 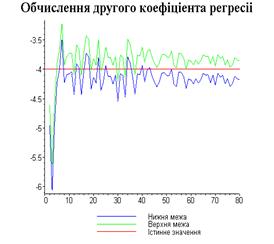
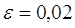
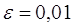
Результати програми для вибірки діапазону 1-40.
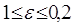
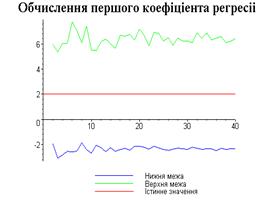 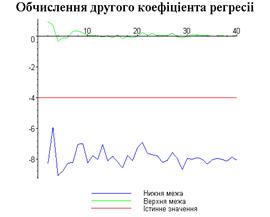
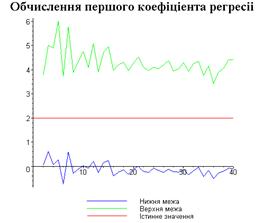 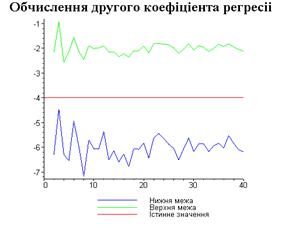
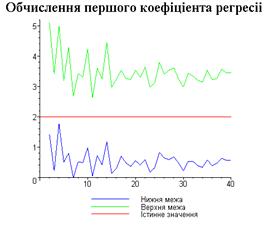 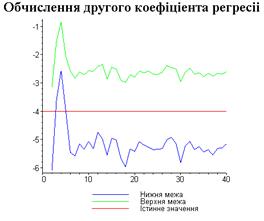
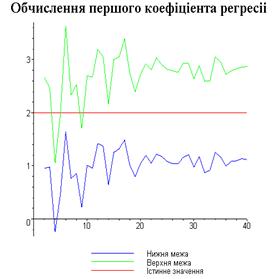 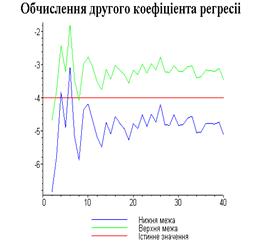
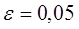
 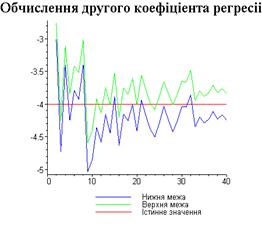
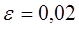
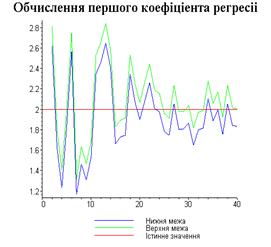 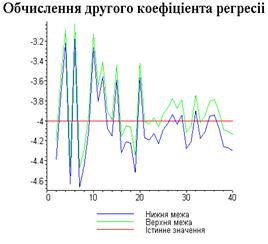
Результати програми для вибірки діапазону 1-20.
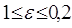
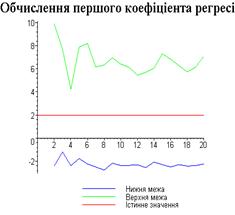 
Результати програми для вибірки діапазону 1-10.
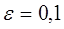
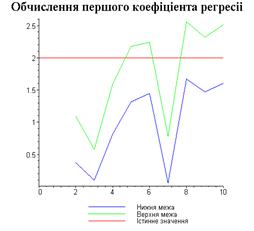 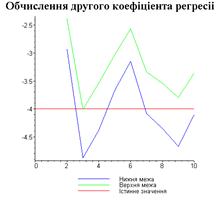
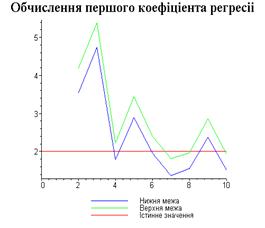 
Результати програми для вибірки діапазону 1-200.
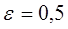
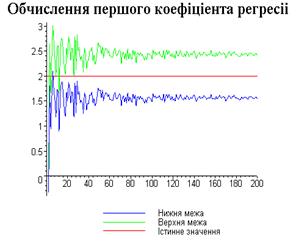 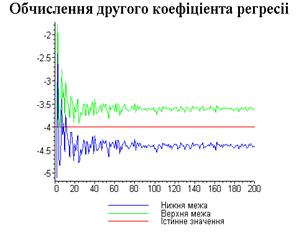
Висновки
В дипломній роботі за допомогою розробленої програми
проведено чисельний експеримент по дослідженню залежності величин довжин
інтервалів, що накривають невідомі параметри регресії, від об’єму вибірки.
З одержаних результатів випливає, що починаючи з
деякого об’єму вибірки спостерігається стабілізація, тобто різниця між верхньою
та нижньою границею інтервалів, що накривають параметри регресії, перестає
зменшуватись. Тому використовувати вибірки об’ємом більше, ніж це порогове
значення є недоцільним, бо це не дає поліпшення результатів. Цей поріг, де
починається стабілізація, не залежить від вектора похибки і приблизно дорівнює
50.
Список використаних джерел
1. Орлов
А.И Прикладная статистика. – М.: Экзамен, 2004.
2. Орлов А.И.,
Орловский И.В. Прикладной многомерный статистический
анализ.
– М.: Наука, 1978.
3. Вощинин А.П., Бочков
А.Ф. Сотиров Г.Р. Интервальный анализ данных
как альтернатива
регрессионному анализу. – Заводская лаборатория,
1990.
4. Вощинин А.П. Интервальный
анализ данных: развитие и перспективы. -
Заводская лаборатория,
2002.
5. Себер Дж. Линейный
регрессионный анализ. – М.: Мир, 1980.
6. Демиденко Е. З.
Линейная и нелинейная регрессии. – М.: Финансы и
статистика, 1981.
7. Дьяконов В.
Maple 6: учебный курс. – СПб.: Питер, 2001.
8. Четыркин Е.М.
Статистические методы прогнозирования. – М.:
Статистика,
1975.
|