Реферат: Анализ случайных процессов в линейных системах радиоэлектронных следящих систем
Реферат: Анализ случайных процессов в линейных системах радиоэлектронных следящих систем
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра РТС
РЕФЕРАТ
На тему:
"Анализ случайных процессов в линейных системах
радиоэлектронных следящих систем"
МИНСК, 2008
Задающее воздействие 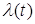 и внутренние возмущения
(флуктуации частоты, фазы, задержки) являются случайными процессами с нормальным
законом распределения, который не изменяется при прохождении процессов через
линейные цепи. Флюктуационная составляющая напряжения на выходе дискриминатора и внутренние возмущения
(флуктуации частоты, фазы, задержки) являются случайными процессами с нормальным
законом распределения, который не изменяется при прохождении процессов через
линейные цепи. Флюктуационная составляющая напряжения на выходе дискриминатора 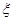 (t) также процесс случайный, и хотя не всегда имеет нормальный
закон распределения, но при прохождении через последующие узкополосные линейные
цепи нормализуется. (t) также процесс случайный, и хотя не всегда имеет нормальный
закон распределения, но при прохождении через последующие узкополосные линейные
цепи нормализуется.
Случайный процесс с нормальным законом распределения
определяется математическим ожиданием и корреляционной функцией. Методы
определения математического ожидания рассмотрены в предыдущем разделе. Рассмотрим
методы определения корреляционной функции и связанной с ней дисперсией
случайных процессов.
Спектральная плотность процесса на выходе и входе линейной
системы связаны зависимостью
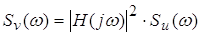 , ,
где 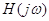 - частотная передаточная функция
системы; - частотная передаточная функция
системы;
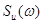 - спектральная плотность процесса
на входе. - спектральная плотность процесса
на входе.
Преобразовав по Фурье правую и левую часть можно определить
корреляционную функцию:
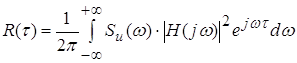 . .
Дисперсия случайного процесса на выходе линейной системы:
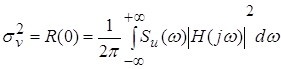 (1) (1)
или:
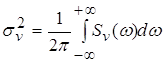 , (2) , (2)
где Sv(w) –двусторонняя
спектральная плотность процесса на выходе системы.
При использовании односторонней спектральной плотности N(f) выражение (2) может быть
записано в виде:
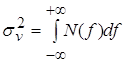 , ,
где 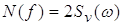 ; ; 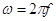 . .
Расчет
дисперсии случайного процесса с помощью стандартных интегралов
Для упрощения вычисления интеграла (6.1) его приводят к
стандартному виду:
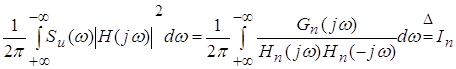 , ,
где 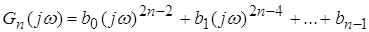 ─ полином четной степени частоты ─ полином четной степени частоты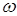 ; ;
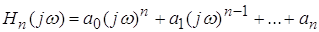 - полином, корни которого
принадлежат верхней полуплоскости комплексной переменной - полином, корни которого
принадлежат верхней полуплоскости комплексной переменной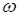 ; n
– степень полинома ; n
– степень полинома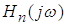 . .
Вычисление производят по формулам:
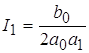 ; ; 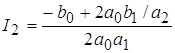 ; ; 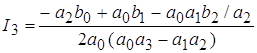 . .
При n>3 формулы для расчетов
можно найти в справочнике.
Условие применения стандартных интегралов: полином под
интегралом должен быть дробно-рациональной функцией переменной и система должна быть
устойчивой. и система должна быть
устойчивой.
Рассмотрим пример расчета дисперсии ошибки слежения в
системе, представленной структурной схемой (рис.1).
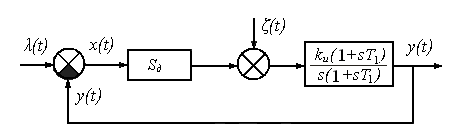
Рис.1. К примеру расчета дисперсии ошибки слежения.
Исходные данные:
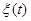 ─ флюктуационная
составляющая, определяемая спектральной плотностью ─ флюктуационная
составляющая, определяемая спектральной плотностью 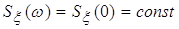 . .
Рассчитаем дисперсию ошибки слежения по формуле дисперсию по
формуле:
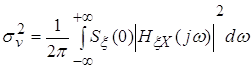 . .
Передаточная функция от воздействия к ошибке
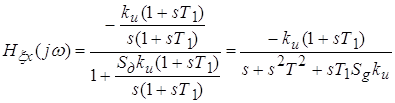 ; ;
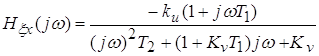 ; ; 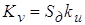 . .
Выполним расчет:
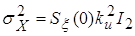 ; ;
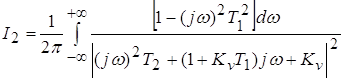 ; ;
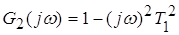 ; ; 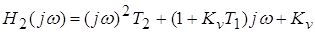 ; ;
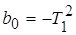 ; ; 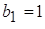 ; ; 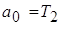 ; ; 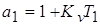 ; ; 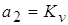 ; ;
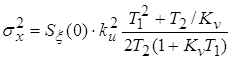 . (3) . (3)
Приведем 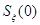 ко входу дискриминатора и упростим
выражение (3) ко входу дискриминатора и упростим
выражение (3)
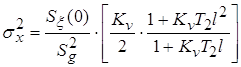 , (4) , (4)
где 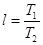 ; ; 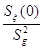 - спектр приведенного ко входу
дискриминатора случайного процесса. - спектр приведенного ко входу
дискриминатора случайного процесса.
Таким образом, дисперсия ошибки слежения пропорциональна
коэффициенту усиления разомкнутого контура следящей системы и спектральной
плотности флюктуационной составляющей.
Если вместо пропорционально-интегрирующего фильтра
использовать интегратор, то: 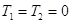 , и , и
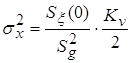 ; ;
Если на вход инерционного звена с передаточной функцией
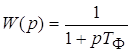
подать шум со спектральной плотностью 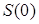 , то дисперсия на выходе
будет равна , то дисперсия на выходе
будет равна
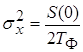 ; ;
Таким образом шум вызывает одинаковый эффект на выходе
инерционной цепи и в следящих системах, содержащих одно интегрирующее звено с
добротностью, обратной постоянной времени 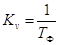 . .
Если следящая система содержит в качестве фильтра
последовательное соединение инерционного звена и интегратора, то в этом случае
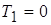 ; ; 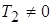 ; ; 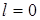 ; ; 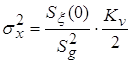 . .
Следовательно, постоянная времени инерционного звена не
влияет на величину флюктуационной ошибки (дисперсию). Это объясняется тем, что
при увеличении 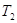 инерционного звена сужается
полоса системы, но одновременно увеличивается максимум АЧХ, а площади под
кривыми не изменяются (рис.2). инерционного звена сужается
полоса системы, но одновременно увеличивается максимум АЧХ, а площади под
кривыми не изменяются (рис.2).
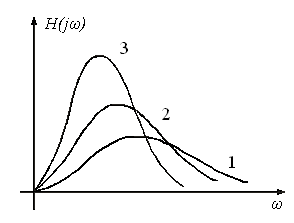
Рис.2. Зависимость АЧХ от постоянной времени инерционного
звена.
Используя (4) можно оптимизировать параметры системы, в
частности 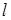 по
критерию минимума флюктуационной ошибки. С этой целью продифференцируем (6.4) по по
критерию минимума флюктуационной ошибки. С этой целью продифференцируем (6.4) по
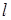 и
приравняем производную нулю. и
приравняем производную нулю.
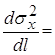 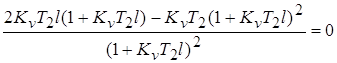 ; ;
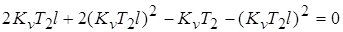 ; ;
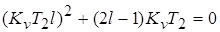 ; ;
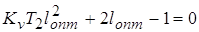 ; ; 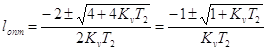 ; ;
при 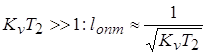 ; ; 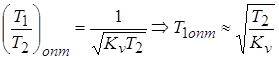 ; ;
Подставив 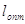 в (4), получим в (4), получим
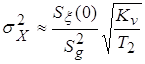 , ,
где 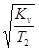 - собственная частота следящей
системы. - собственная частота следящей
системы.
Если задающее воздействие представлено спектральной
плотностью неточность его воспроизведения также оценивается дисперсией. Рассмотрим
пример (рис.3).
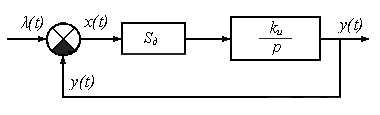
Рис.3
Пусть 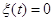 ; ; 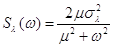 , ,
где 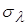 ─ дисперсия задающего
воздействия; ─ дисперсия задающего
воздействия;
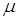 - параметр, определяющий ширину
спектра. - параметр, определяющий ширину
спектра.
Определим величину дисперсии ошибки слежения 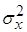 , обусловленную
неточностью воспроизведения задающего воздействия. , обусловленную
неточностью воспроизведения задающего воздействия.
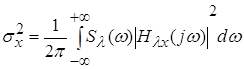 ; ;
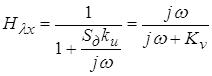 , ,
где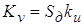 ; ; 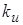 - коэффициент передачи
интегратора; - коэффициент передачи
интегратора;
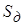 - крутизна дискриминационной
характеристики. - крутизна дискриминационной
характеристики.
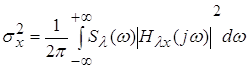 ; ; 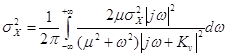 ; ;
приведем выражение к стандартному виду:
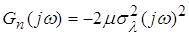 ; ;
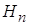 (jw) =( (jw) =(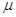 +jw) (Kv+jw) =(jw) 2 +( +jw) (Kv+jw) =(jw) 2 +(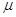 +Kv) jw+ +Kv) jw+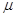 Kv; Kv;
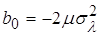 ; ; 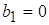 ; ;
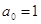 ; ; 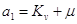 ; ; 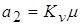 ; ; 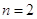 ; ;
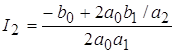 ; ; 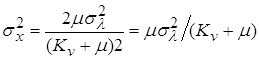 ; ;
При увеличении 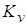 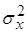 уменьшается, в то время как в
первом примере уменьшается, в то время как в
первом примере 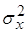 увеличивается. увеличивается.
Эквивалентная шумовая полоса следящих систем
Под эквивалентной шумовой полосой следящей системы понимают
полосу пропускания эквивалентной системы, имеющей прямоугольную АЧХ, одинаковое
с исходной системой ее значение на нулевой частоте и одинаковую дисперсию на
выходе при воздействии на входы систем белого шума (рис.4).
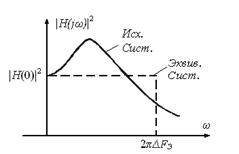
Рис.4. АЧХ исходной и эквивалентной систем.
Чтобы определить полосу пропускания 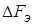 используем условие равенства
дисперсий: используем условие равенства
дисперсий:
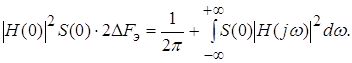
Отсюда
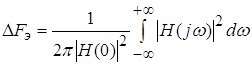 . .
Использование значения эквивалентной шумовой полосы
позволяет упростить вычисление дисперсии:
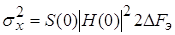 ; ; 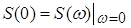 . .
Если 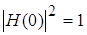 , то , то 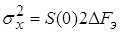 , или , или 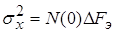 , ,
где 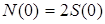 ─ односторонняя
спектральная плотность. ─ односторонняя
спектральная плотность.
Формулы для расчета эквивалентной шумовой полосы систем
приведены в табл.1
Таблица 1. Формулы для расчета эквивалентной шумовой полосы.
Для решения задачи оптимизации необходимо определить
структуру системы, предъявляемые требования и ограничения, накладываемые на
систему, описать воздействия и возмущения, выбрать критерий оптимизации и метод.
Оптимизируем параметры kи2 и T1 в системе (рис.5), в которой задающее воздействие λ(t) – детерминированная
функция, а возмущение ─ случайный процесс ξ(t).
В качестве критерия оптимизации используем критерий минимума
среднего квадрата ошибки:
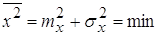 ; (5) ; (5)
где 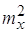 - квадрат математического
ожидания ошибки слежения. - квадрат математического
ожидания ошибки слежения.
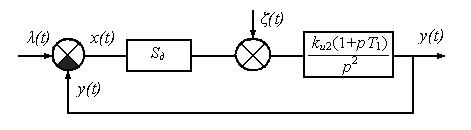
Рис.5. Структурная схема оптимизируемой системы.
Исходные данные:
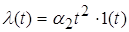 ; ; 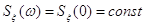 . .
Необходимо определить 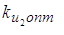 и и 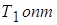 по критерию (5). по критерию (5).
Величина математического ожидания (динамической ошибки) определяется
выражением
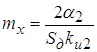 . .
Величина дисперсии ошибки:
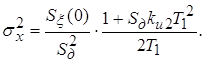
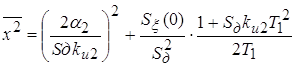 . (6) . (6)
Для определения оптимальных значений параметров
воспользуемся методом дифференцирования:
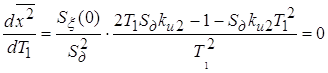 . .
Из этого уравнения определяем
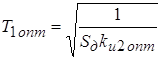 . (7) . (7)
Подставив в исходное уравнение (6) вместо T1
его оптимальное значение (7) и продифференцировав по переменной kи2, найдем ее оптимальное значение
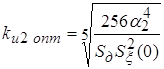 . .
Пусть задающее воздействие является случайным процессом с
нулевым математическим ожиданием и спектральной плотностью
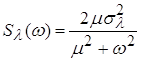
Флюктуационная составляющая характеризуется спектральной
плотностью 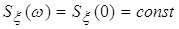 . .
В качестве фильтра используется идеальный интегратор:
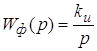 . .
Найдем оптимальное значение коэффициента передачи
интегратора 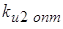 по
критерию минимума суммарной ошибки слежения: по
критерию минимума суммарной ошибки слежения:
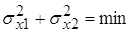 , ,
где 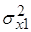 ─ величина дисперсии ошибки,
обусловленная неточным воспроизведением входного воздействия; ─ величина дисперсии ошибки,
обусловленная неточным воспроизведением входного воздействия; 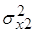 ─ величина
дисперсии ошибки обусловленная воздействием флюктуационной составляющей. ─ величина
дисперсии ошибки обусловленная воздействием флюктуационной составляющей.
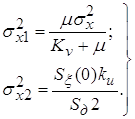
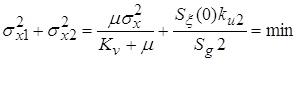 . (8) . (8)
Продифференцируем (8) по 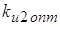 и приравняем производную нулю. В
результате получим и приравняем производную нулю. В
результате получим
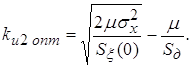 . .
Память следящих систем
Радиотехнические системы работают в условиях многолучевого
распространения радиоволн, поэтому при приеме сигнала наблюдается эффект
замирания сигнала. Попадание на вход приемника мощной широкополосной помехи
приводит к смещению рабочей точки характеристики активного элемента на
нелинейный участок характеристики и в результате – к подавлению полезного
сигнала мощной помехой. Сигнал на входе следящей системы пропадает, что
эквивалентно размыканию контура. На структурной схеме (Рис.6) это явление можно
отобразить введением двух ключей Кл1 и Кл2. Пропадание сигнала приводит к
размыканию ключа Кл1 и переводу ключа Кл2 в положение 2, поскольку меняется
характер флюктуаций.
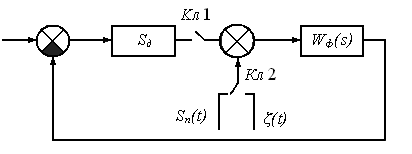
Рис.6. Структурная схема следящей системы с учетом
пропадания полезного сигнала на входе.
Если в режиме слежения закон распределения ошибки нормальный
с нулевым математическим ожиданием и в момент времени 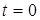 следящая система разомкнулась, то
через время следящая система разомкнулась, то
через время 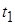 ,
характер распределения ошибки слежения изменится: увеличится математическое
ожидание и дисперсия. Если в момент ,
характер распределения ошибки слежения изменится: увеличится математическое
ожидание и дисперсия. Если в момент 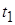 значение ошибки не выходит за
пределы апертуры дискриминационной характеристики, то появление сигнала
приведет к восстановлению режима слежения. Если же значение ошибки не выходит за
пределы апертуры дискриминационной характеристики, то появление сигнала
приведет к восстановлению режима слежения. Если же 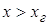 , то происходит срыв слежения. , то происходит срыв слежения.
Вероятность того, что через 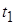 после пропадания сигнала ошибка
слежения не превышает после пропадания сигнала ошибка
слежения не превышает 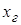 определяет память следящей
системы: определяет память следящей
системы:
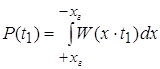 . .
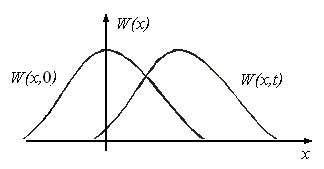
Рис.7. Распределение плотности вероятности ошибки слежения.
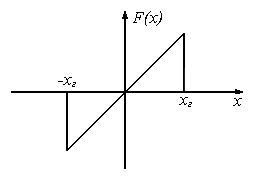
Рис.8. Дискриминационная характеристика.
Рассмотрим пример.
Пусть следящая система имеет два интегратора (рис.9).
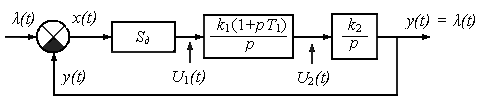
Рис.9. Структурная схема системы.
Задающее воздействие определяется линейной зависимостью
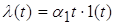 ; ;
Поскольку система является астатической с астатизмом второго
порядка установившееся значение ошибки равно нулю, т.е.
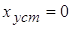 . .
Следовательно,
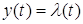 ; ; 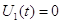 , а , а 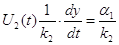 , ,
т.е. напряжение на входе второго интегратора пропорционально
скорости изменения задающего воздействия 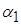 . .
Таким образом, система отслеживает скорость изменения
входного процесса не по рассогласованию а по памяти. При пропадании сигнала на
вход система будет отслеживать его изменение, если скорость не изменятся. При
восстановлении сигнала ошибка будет минимальной, или равной нулю (в реальной
ситуации срыв может произойти в результате флюктуаций управляемой величины под
воздействием помех).
Память следящих систем определяется числом интегрирующих
звеньев. Одно звено обеспечивает память по положению, два – по скорости, три –
по ускорению.
Таким образом, система с астатизмом n
–го порядка обладает памятью по n-1 производной
задающего воздействия.
ЛИТЕРАТУРА
1. Коновалов. Г.Ф. Радиоавтоматика: Учебник для вузов. – М.:
Высш. шк., 2000.
2. Радиоавтоматика: Учеб. пособие для вузов. / Под ред.В.А. Бесекерского.
- М.: Высш. шк., 2005.
3. . Первачев С. В. Радиоавтоматика: Учебник для вузов. - М.:
Радио и связь, 2002.
4. Цифровые системы фазовой синхронизации / Под ред. М.И. Жодзишского
– М.: Радио, 2000
|