Курсовая работа: Використання елементарних перетворень для знаходження оберненої матриці
Курсовая работа: Використання елементарних перетворень для знаходження оберненої матриці
Міністерство освіти і науки України
Факультет інформатики
Курсова робота
Тема:
“Використання елементарних перетворень
для знахожження оберненої матриці ”
Виконав студент ІІ-го курсу
Факультету
інформатики
Заочної форми
навчання
Науковий керівник:
Ужгород 2009
Зміст. 2
Вступ. 3
1.
Теория. 4
2.
Опис програми. 8
3.
Програма. 10
Висновок. 45
Список
використаної літератри. 46
Квадратна матриця називається виродженою (для
особливої), якщо її визначник дорівнює нулю, і невиродженою (чи неособливої) - у
протилежному випадку. Відповідно лінійне перетворення невідомих називається
виродженим чи невиродженим у залежності від того, чи буде дорівнює чи нулю
відмінний від нуля визначник з коефіцієнтів цього приобразования. З теореми
випливає наступне твердження:
Добуток матриць, хоча б одна з яких вироджена,
буде вродженою матрицею.
Добуток будь-яких невироджених матриць саме
буде невирожденою матрицею. Звідси випливає, через зв'язок, що існує між
множенням матриць і послідовним виконанням лінійних перетворень, таке
твердження: результат послідовного виконання декількох лінійних перетворень
тоді і тільки тоді буде невиродженим перетворенням, якщо всі задані
перетворення невироджені.
Квадратна матриця називається виродженою (для
особливої), якщо її визначник дорівнює нулю, і невиродженою (чи неособливої) - у
протилежному випадку. Відповідно лінійне перетворення невідомих називається
виродженим чи невиродженим у залежності від того, чи буде дорівнює чи нулю
відмінний від нуля визначник з коефіцієнтів цього приобразования. З теореми
випливає наступне твердження:
Добуток матриць, хоча б одна з яких вироджена,
буде вродженою матрицею.
Добуток будь-яких невироджених матриць саме
буде невирожденою матрицею. Звідси випливає, через зв'язок, що існує між
множенням матриць і послідовним виконанням лінійних перетворень, таке
твердження: результат послідовного виконання декількох лінійних перетворень
тоді і тільки тоді буде невиродженим перетворенням, якщо всі задані
перетворення невироджені.
Роль одиниці у множенні матриць грає одинична
матриця
причому вона перестановочна з будь-якою
матрицею А даним порядком
АЕ=ЕА=А (1)
Доводяться ці чи рівності безпосереднім
приминением правилаумножения матриць, чи ж на підставі зауваження, що еденичная
матриця відповідає тотожному лінійний приобразованию невідомих
x1=y1
x2= y2
... ... ... .
xn= yn
Виконання якого до чи після будь-якого іншого
лінійного переутворення, очевидно не змінює цього останнього.
Помітимо, що матриця Е є єдиною матрицею, що
задовольняє умові (1) при будь-якій матриці А. Дійсно, якби існувала матриця Е'
з цією же властивістю, то ми мали б
E’E=E’, E’E=E,
звідки E’=E.
Питання про існування для даної матирцы А
зворотної матриці виявляється болеее складним. Через некомутативности множення
матриць ми будемо говорити зараз про праву зворотну матрицю, тоесть про таку
зворотну матрицю А-1
Що добуток матриці А праворуч на цю матрицю
дає еденичную матрицю,
AA-1=E (2)
Якщо матриця А вырожденная, то, якби матриця
А-1 існувала, добуток, що коштує в лівій частині рівності (2), було б, як ми
знаємо, вырожденной матрицею, у той час як насправді матриця Е, що коштує в
правій частині цієї рівності, є невырожденной, тому що його визначник дорівнює
еденице. Таким чином, вырожденная матриця не може мати правої зворотної матриці.
Такого ж розуміння показують, сто вона не має і лівої зворотний і тому для
вырожденной матриці обратеая матриця воопше не існує.
Переходячи до випадку невырожденной матриці,
уведемо спочатку наступне допоміжне поняття. Нехай дана матриця n-го порядку

a11 a12... a1n
a21 a22... a2n
А=... ... ... ... ... ... ... ... .
an1 an1... ann
Матриця

a11 a12... a1n
A*= a21 a22... a2n
... ... ... ... ... ... ... ... .
an1 an1... ann
Складання з алгебраїчних доповнень до
елементів матриці А, причому алгебраїчне доповнення до елементу aіj коштує на
перетинанні j-й рядка й і-го стовпця, називається приєднаної (чи взаємної) до
матриці А.
Знайдемо добуток АА* і А*А. Використовуючи
відому формулу розкладання визначника по чи рядку стовпцю, а також теорему про
суму добутків елементів будь-якого рядка (стовпця) визначника на алгебраїчні
доповнення до відповідних елементів іншого рядка (стовпця), і позначаючи через
d визначник матриці А,
d=|A|,
ми одержимо наступні рівності:
 d
0...0 d
0...0
0 d...0
АА*=А*А=... ... ... . . (3)
0 0... d
Звідси випливає, що якщо матриця А
невырожденная, те її присоедененная матриця А* також буде невырожденной,
причому визначник d* матриці А* дорівнює (n-1) - й ступеня визначника d матриці
А.
Справді, переходячи від рівностей (3) до
рівності між визначниками, ми одержимо
dd*= dn,
звідки d≠0
d*= dn-1
Тепер можна довести існування зворотної
матриці для всякої не виродженої матриці А и знайти її вид. Помітимо спочатку,
що якщо ми розглянемо добуток двох матриць АВ і всі елементи одногоиз
множників, наприклад У, розділимо на те саме число d, те всі елементи добутку
АВ також розділяться на це ж число: для доказу потрібно лише згадати визначення
множення матриць. Таки мобразом, якщо
d=|A|≠0
те з рівностей (3) випливає, що зворотною
матрицею для А буде служити матриця, що виходить із присоедененной матриці А*
розподілом усіх її елементів на d:
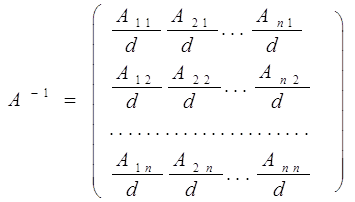
Дійсно, з (3) випливають рівності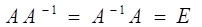
(4)
Ще раз підкреслимо, що в і-й рядку матриці А-1
коштують алгебраическиедополнения до елементів і-го стовпця визначника |А|,
ділені на d=|A|.
Легко довести що матриця А-1 є єдиною
матрицею, що задовольняє умові (4) для даної невырожденной матриці А. Дійсно,
якщо матриця З така, що
АС=СА=Е
то
САА-1=С(АА-1) =СЕ=С
САА-1=(СА) А-1=ЕА=А-1
Звідки С=А-1.
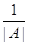 З (4) і теореми про множення визначників випливає, що визначник матриці
А-1 дорівнює, так що ця матриця так само З (4) і теореми про множення визначників випливає, що визначник матриці
А-1 дорівнює, так що ця матриця так само
буде невиродженою. Зворотної для неї служить
матриця А.
Якщо тепер дані квадратні матриці n-го порядку
А и В, з яких А-невырожденная, а В - довільна, то ми можемо виконати правий і
лівий розподіл У на А, тобто, вирішити матричні рівняння
AX=B, YA=B (5)
Для цього, через асоціативності множення
матриць, досить покласти
X=A-1B, Y=BA-1,
причому ці рішення рівнянь (5) буду, через
некоммутативности множення матриць, у загальному випадку різними.
Програма Matrtest. pas являється демо
программою, котра показує роботу процедур з модуля Matr. pas.
Модуль програми Matr. pas – в ній розміщені
процедури і функції, котрі роблять перетворення матриць.
У файлі – Time. dat записані коефіціенти
матриці, розмірність матриці. Він мусить містити в собі початкову матрицю, і її
розмірність, тому, що програма без цих даних працювати не буде.
Нижче приведений “скрин” програми, тобто
вигляд програми в роботі.
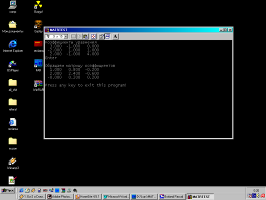
3. Програма
{============================Matrtest. pas=========================}
Uses matr;
Var A,C: MAtrix;
Begin
A. VMT; C. VMT;
Writeln(' Коэффициеты уравнения ');
A. ReadOfText('time',' Коэффициеты уравнения ');
A. WriteToText('con',7,3);
Write('Enter'); Readln;
Writeln('Обращаем матрицу коэффициентов');
C. RevWithGauss(A);
C. WriteToText('con',7,3);
Write('Enter'); Readln;
End.
{============================ Matr. pas
==========================}
{$A+,B-,D-,E-,F+,G+, I-,L-,N+,O-,P-,Q-,R-,S-,T+,V+,X+}
{$M 24000,32,655360}
Unit Matr;
Interface
Const
CTooManySize=1;
CBadPosition=2;
CFileNotFound=3;
CFileError=4;
CReadError=5; {A}
CWriteError=6; {A}
COutOfData=7;
CBadOperands=8;
CMulError=9; {A}
CSearchError=10;
CNotExist=11;
CMNotSquare=12;
CAddError=13; {A}
CReversError=14; {A}
CMDegenerate=15;
CUnkNownError=16;
CMDgError=17; {A}
CMSqrError=18; {A}
CDetError=19; {A}
CSortError=20; {A}
CDGaussError=21; {A}
CCuanZeeroError=22; {A}
CSwapError=23; {A}
CMulToNumError=24; {A}
CStopped=25;
CDegrError=26; {A}
CIgError=27; {A}
CZFE=28;
Type
TOE=Extended;
Ar=Array [1. . (Word(Pred(0)) +1) div
SizeOf(TOE)] of TOE;
Ar31=Array [1. .31,1. .31] of
TOE;
Ar63=Array [1. .63,1. .63] of
TOE;
Tabl=Object
CBars,CLines: Byte;
M: Pointer; {**}
SizeInMemory: Word; {**}
Errors: Set of Byte;
Exist: Boolean;
Constructor VMT;
Procedure DataInit(L,B: Byte); Virtual;
Procedure SetE(I,J: Byte; E: TOE);
Function GetE(I,J: Byte): TOE;
Procedure Del;
Procedure ReadOfText(Name: String; Search: String);
Procedure WriteToText(Name: String; F1,F2: Byte);
Procedure AllClear; Virtual; {}
Procedure Let(Var A); Virtual;
Procedure ZeeroFill;
{ Errors }
Procedure TooManySize; Virtual;
Procedure BadPosition; Virtual;
Procedure FileNotFound; Virtual;
Procedure FileError; Virtual;
Procedure ReadError; Virtual;
Procedure WriteError; Virtual;
Procedure OutOfData; Virtual;
Procedure SearchError; Virtual;
Procedure NotExist; Virtual;
Procedure UnkNownError; Virtual;
Procedure AnyError; Virtual;
Procedure ZFE; Virtual;
End;
Line=Set of Byte;
Mem=Record
mPlus: Boolean;
mDirection: Boolean;
mSortLines: Boolean;
mBeginZeero: Boolean;
mSpecialSort: Boolean;
mGauss: Boolean;
mDetForRev: Boolean;
End;
Matrix=Object(Tabl)
Lin,Bar: Line;
Plus: Boolean;
Direction: Boolean;
SortLines: Boolean;
BeginZeero: Boolean;
SpecialSort: Boolean;
Chek: Integer;
Gauss: Boolean;
DetForRev: Boolean; {ўбҐ Ї а ¬Ґвал -
ўгв२Ґ}
{Mem}
Procedure AllClear; virtual;
Function SIgn(C: Word): TOE;
Procedure Revers(Var A: Matrix); {®Ўа й Ґв
бҐЎп ¬Ґ¤«Ґл¬ бЇ®б®Ў®¬}
Procedure RevWithGauss(Var A: Matrix); {®Ўа й Ґв
ᥡ ў®а®зҐл¬ бЇ®б®Ў®¬}
Procedure InnerRevers(Var A: Matrix); Virtual;
Procedure ZeeroSortBars;
Procedure ZeeroSortLines;
Procedure UniversalSort;
Function DetWithGauss: TOE; Virtual; {®Ўа й Ґв
бҐЎп ў®а®зҐл¬ (Ўлбвал¬) бЇ®б®Ў®¬}
Function CuanZeeroInLine(L1: Integer): Integer;
Procedure SwapLines(L1,L2: Integer); Virtual;
Procedure SwapBars(B1,B2: Integer);
Function CuanZeeroInBar(B1: Integer): Integer;
Procedure SpecialSortLines;
Procedure SpecialSortBars;
Procedure SelfClear; Virtual;
Procedure StepRevers; Virtual;
Procedure RemSettings(Var FM: Mem); Virtual;
Procedure RestoreSettings(Var FM: Mem); Virtual;
Procedure MSqr(Var A: Matrix); {ў®§ў®¤Ёв ўбҐ
н«Ґ¬Ґвл ¬ ваЁжл ў Єў ¤а в}
Procedure MDg(Var A: Matrix);
{errors}
Procedure BadOperands; Virtual;
Procedure MulError; Virtual;
Procedure MNotSquare; Virtual;
Procedure AddError; Virtual;
Procedure ReversError; Virtual;
Procedure MDegenerate; Virtual;
Procedure MDgError; Virtual;
Procedure MSqrError; Virtual;
Procedure DetError; Virtual;
Procedure SortError; Virtual;
Procedure DGaussError; Virtual;
Procedure CuanZeeroError; Virtual;
Procedure SwapError; Virtual;
Procedure MulToNumError; Virtual;
Procedure Stopped; Virtual;
Procedure DegrError; Virtual;
Procedure IgError; Virtual;
End;
Matrix31=Object(Matrix)
Function DetWithGauss: TOE; Virtual;
Procedure SwapLines(L1,L2: Integer); Virtual;
End;
Matrix63=Object(Matrix)
Function DetWithGauss: TOE; Virtual;
Procedure SwapLines(L1,L2: Integer); Virtual;
End;
Implementation
{**************************************************************************}
Procedure TAbl. ZeeroFill;
Var i,j: Integer;
Begin
IF Not Exist Then Begin NotExist; ZFE; Exit; End;
IF (Errors<> [0]) Then Begin ZFE; Exit; End;
For i: =1 to CLines do
For j: =1 to CBars do
SetE(i,j,0);
End;
Procedure Tabl. Let(Var A);
Begin
End;
Procedure Tabl. AllClear;
Begin
CBars: =0;
CLines: =0;
SizeInMemory: =0;
Errors: = [0] ;
M: =Nil;
End;
Procedure Tabl. DataInit(L,B: Byte);
Begin
IF Exist Then Del;
AllClear;
IF 1.0*SizeOf(TOE) *L*B>(Word(Pred(0))
+1) *1.0 Then Begin TooManySize; Exit; End;
CBars: =B;
CLines: =L;
SizeInMemory: =SizeOf(TOE) *CBars*CLines;
If MaxAvail < SizeInMemory Then Begin
TooManySize; Exit; End;
GetMem(M,SizeInMemory);
Exist: =True;
End;
Procedure Tabl. SetE(I,J: Byte; E: TOE);
Begin
IF Errors<> [0] Then Exit;
IF Not Exist Then Begin NotExist; Exit; End;
IF (I>CLines) or (J>CBars) or (I<1) or
(J<1) Then Begin BadPosition; Exit; End;
Ar(M^) [((I-1) *CBars+J)]: =E;
End;
Function Tabl. GetE(I,J: Byte): TOE;
Begin
IF Errors<> [0] Then Exit;
IF Not Exist Then Begin NotExist; Exit; End;
IF (I>CLines) or (J>CBars) or (I<1) or
(J<1)
Then
Begin
GetE: =0.0;
BadPosition;
End
Else
GetE: =Ar(M^) [((I-1) *CBars+J)] ;
End;
Procedure Tabl. Del;
Begin
IF Errors<> [0] Then Exit;
IF Not Exist Then Begin NotExist; Exit; End;
IF SizeInMemory<>0 Then
FreeMem(M,SizeInMemory);
AllClear;
Exist: =False;
End;
Procedure Tabl. ReadOfText(Name: String; Search:
String);
Var F: Text;
I,J: Byte;
Prom: TOE;
Help: Integer;
Function Searcher: Boolean;
Var Prom: String;
Begin
Repeat
Readln(F,Prom);
IF IOResult<>0 Then Begin ReadError; Close(F);
Exit; End;
Until (EOF(F)) or (Pos(Search,Prom) <>0);
IF Pos(Search,Prom) =0
Then
Begin
SearchError;
Searcher: =False;
End
Else Searcher: =True;
End;
Begin
IF Exist Then Del;
Assign(F,Name);
{$I-}
Reset(F);
IF IOResult=2 Then Begin FileNotFound; ReadError;
Exit; End;
IF IOResult<>0 Then Begin FileError; ReadError;
Exit; End;
IF Not Searcher Then Exit;
Readln(F,CLines);
IF IOResult<>0 Then Begin AllClear; ReadError;
Close(F); Exit; End;
Readln(F,CBars);
IF IOResult<>0 Then Begin AllClear; ReadError;
Close(F); Exit; End;
DataInit(CLines,CBars);
IF Errors<> [0] Then Exit;
IF Not Exist Then Exit;
For I: =1 to CLines do
For J: =1 to CBars do
Begin
Read(F,Prom);
IF (EOF(F)) and (I<>CLines) And
(I<>CBars) Then Begin Del; OutOfData; ReadError; Close(F); Exit; End;
IF IOResult<>0 Then Begin Del; ReadError;
Close(F); Exit; End;
SetE(I,J,Prom);
End;
Close(F);
{$I+}
End;
Procedure Tabl. WriteToText(Name: String; F1,F2:
Byte);
Var F: Text;
I,J: Byte;
Begin
IF Errors<> [0] Then Exit;
IF Not Exist Then Begin NotExist; WriteError; Exit;
End;
Assign(F,Name);
{$I-}
ReWrite(F);
IF IOResult<>0 Then Begin FileError; WriteError;
Exit; End;
For I: =1 to CLines do
Begin
For J: =1 to CBars do
Begin
Write(F,GetE(I,J): F1: F2,' ');
IF IOResult<>0 Then Begin Close(F); WriteError;
Exit; End;
End;
Writeln(F)
End;
Close(F);
{$I+}
End;
Procedure Tabl. TooManySize;
Begin
Errors: =Errors+ [CTooManySize] ;
AnyError
End;
Procedure Tabl. BadPosition;
Begin
Errors: =Errors+ [CBadPosition] ;
AnyError
End;
Procedure Tabl. FileNotFound;
Begin
Errors: =Errors+ [CFileNotFound] ;
AnyError
End;
Procedure Tabl. FileError;
Begin
Errors: =Errors+ [CFileError] ;
AnyError
End;
Procedure Tabl. ReadError;
Begin
Errors: =Errors+ [CReadError] ;
AnyError
End;
Procedure Tabl. WriteError;
Begin
Errors: =Errors+ [CWriteError] ;
AnyError
End;
Procedure Tabl. OutOfData;
Begin
Errors: =Errors+ [COutOfData] ;
AnyError
End;
Procedure Tabl. SearchError;
Begin
Errors: =Errors+ [CSearchError] ;
AnyError
End;
Procedure Tabl. NotExist;
Begin
Errors: =Errors+ [CNotExist] ;
AnyError
End;
Procedure Tabl. ZFE;
Begin
Errors: =Errors+ [CZFE] ;
AnyError
End;
Procedure Tabl. UnkNownError;
Begin
Errors: =Errors+ [CUnkNownError] ;
AnyError
End;
Procedure Tabl. AnyError;
Begin
End;
Constructor TAbl. VMT;
Begin
Exist: =False;
End;
Procedure Matrix. MSqr;
Var i,j: Integer;
Begin
IF Not A. Exist Then Begin A. NotExist; BadOperands;
MSqrError; Exit; End;
IF A. Errors<> [0] Then Begin MsqrError;
Exit; End;
IF Self. Exist Then Del;
Self. DataInit(A. CLines,A. CBars);
For i: =1 to CLines do
For j: =1 to CBars do
SetE(i,j,Sqr(A. GetE(i,j)));
Self. SelfClear;
End;
Procedure Matrix. MDg;
Var i,j: Integer;
Begin
IF Not A. Exist Then Begin A. NotExist; BadOperands;
MDgError; Exit; End;
IF A. Errors<> [0] Then Begin MDgError; Exit;
End;
IF A. CLines<>A. CBars Then Begin
MNotSquare; MDgError; Exit; End;
IF Exist Then Del;
DataInit(A. CLines,A. CBars);
For i: =1 to A. CLines do
For j: =1 to A. CBars do
IF i=j Then SetE(i,j,A. GetE(i,j))
Else SetE(i,j,0);
Self. SelfClear;
End;
Procedure Matrix. BadOperands;
Begin
Errors: =Errors+ [CBadOperands] ;
AnyError;
End;
Procedure Matrix. MulError;
Begin
Errors: =Errors+ [CMulError] ;
AnyError;
End;
Procedure Matrix. MDgError;
Begin
Errors: =Errors+ [CMDgError] ;
AnyError;
End;
Procedure Matrix. SortError;
Begin
Errors: =Errors+ [CSortError] ;
AnyError;
End;
Procedure Matrix. DetError;
Begin
Errors: =Errors+ [CDetError] ;
AnyError;
End;
Procedure Matrix. DGaussError;
Begin
Errors: =Errors+ [CDGaussError] ;
AnyError;
End;
Procedure Matrix. MSqrError;
Begin
Errors: =Errors+ [CMSqrError] ;
AnyError;
End;
Procedure MAtrix. CuanZeeroError;
Begin
Errors: =Errors+ [CCuanZeeroError] ;
AnyError;
End;
Procedure MAtrix. SwapError;
Begin
Errors: =Errors+ [CSwapError] ;
AnyError;
End;
Procedure Matrix. MulToNumError;
Begin
Errors: =Errors+ [CMulToNumError] ;
AnyError
End;
Procedure Matrix. DegrError;
Begin
Errors: =Errors+ [CDegrError] ;
AnyError
End;
Procedure Matrix. IgError;
Begin
Errors: =Errors+ [CIgError] ;
AnyError
End;
Procedure MAtrix. SelfClear;
Begin
Lin: = [0] ;
Bar: = [0] ;
Plus: =True;
Direction: =True;
SortLines: =True;
BeginZeero: =True;
SpecialSort: =False;
Chek: =0;
Gauss: =False;
DetForRev: =False;
End;
Procedure Matrix. AllClear;
Begin
inherited AllClear;
SelfClear;
End;
Procedure Matrix. Revers;
VAr FM: Mem;
Begin
Gauss: =False;
InnerRevers(A);
End;
Procedure Matrix. RevWithGauss;
Var FM: Mem;
Begin
Gauss: =True;
InnerRevers(A);
End;
Procedure Matrix. InnerRevers;
Var P,A1: Matrix;
D: TOE;
i,j: Integer;
Var Ver: TOE;
Var FM: Mem;
Begin
IF Not A. Exist Then Begin A. NotExist; BadOperands;
ReversError; Exit; End;
IF (A. Errors<> [0]) Then Begin Exit; ReversError;
End;
IF (A. CBars<>A. Clines) Then Begin
BadOperands; ReversError; Exit; End;
P. VMT;
P. DataInit(A. CLines,A. CBars);
A1. VMT;
A1: =A;
IF A1. CLines=31 Then Begin Matrix31(A1). VMT;
A1. Exist: =True; End;
IF A1. CLines=63 Then Begin Matrix63(A1). VMT;
A1. Exist: =True; End;
IF Gauss Then D: =A1. DetWithGauss;
IF D=0 Then
Begin
MDegenerate;
ReversError;
Exit;
End;
DetForRev: =True;
For i: =1 to P. Clines do
Begin
A. StepRevers;
For j: =1 to P. CBars do
Begin
A1. Lin: =A1. Lin+ [i] ;
A1. Bar: =A1. Bar+ [j] ;
IF Gauss Then Ver: =A1. DetWithGauss;
IF (A1. Errors<> [0]) or (A. Errors<>
[0]) Then Begin ReversError; Exit; End;
P. SetE(j, i,(Ver) *Sign(i+j) /D);
A1. Lin: =A1. Lin- [i] ;
A1. Bar: =A1. Bar- [j] ;
End;
End;
IF Self. Exist Then Self. del;
Self: =P;
Self. SelfClear;
End;
Procedure Matrix. SwapBars(B1,B2: Integer);
Var Prom: TOE;
i: Integer;
Begin
IF Not Exist Then BEgin NotExist; SwapError; Exit;
End;
IF (Errors<> [0]) Then Begin SwapError; Exit;
End;
For i: =1 to CLines do
Begin
Prom: =GetE(i,B1);
SetE(i,B1,GetE(i,B2));
SetE(i,B2,Prom)
End;
End;
Function Matrix. CuanZeeroInBar(B1: Integer): Integer;
Var i: Integer;
Sum: Integer;
Begin
IF Not Exist Then Begin NotExist; CuanZeeroError;
Exit; End;
IF (Errors<> [0]) Then Begin
CuanZeeroError; Exit; End;
Sum: =0;
IF Not SpecialSort
Then
For i: =1 to CLines do IF GetE(i,B1) =0 Then
Inc(Sum) else
Else
IF BeginZeero
Then
Begin
Sum: =1;
While (GetE(Sum,B1) =0) and (Sum<=CLines) do
inc(Sum);
Dec(Sum);
End
Else
Begin
Sum: =CLines;
While (GetE(Sum,B1) =0) and (Sum>0) do
Dec(Sum);
Sum: =Clines-Sum;
End;
CuanZeeroinBar: =Sum;
End;
Procedure Matrix. ZeeroSortBars;
Var i,j: Integer;
Max,NMax,CZ: Integer;
FM: Mem;
Begin
IF Not Exist Then Begin NotExist; Exit; End;
IF (Errors<> [0]) Then Exit;
RemSettings(FM);
SortLines: =False;
SpecialSort: =False;
UniversalSort;
RestoreSettings(FM);
End;
Function Matrix. CuanZeeroinLine(L1: Integer):
Integer;
Var i: Integer;
Sum: Integer;
Begin
IF Not Exist Then Begin NotExist; CuanZeeroError;
Exit; End;
IF (Errors<> [0]) Then Begin
CuanZeeroError; Exit; End;
Sum: =0;
IF Not SpecialSort
Then
For i: =1 to CBars do IF GetE(L1, i) =0 Then
Inc(Sum) else
Else
IF BeginZeero
Then
Begin
Sum: =1;
While (GetE(L1,Sum) =0) and (Sum<=CBars) do
inc(Sum);
Dec(Sum);
End
Else
Begin
Sum: =CBars;
While (GetE(L1,Sum) =0) and (Sum>0) do
Dec(Sum);
Sum: =CBars-Sum;
End;
CuanZeeroinLine: =Sum;
End;
Procedure Matrix. SwapLines(L1,L2: Integer);
Var Prom: TOE;
i: Integer;
Begin
IF Not Exist Then Begin NotExist; SwapError; Exit;
End;
IF (Errors<> [0]) Then Begin SwapError; Exit;
End;
For i: =1 to CBars do
Begin
Prom: =GetE(L1, i);
SetE(L1, i,GetE(L2, i));
SetE(L2, i,Prom)
End;
End;
Procedure Matrix. ZeeroSortLines;
VAr FM: Mem;
Begin
IF Not Exist Then Begin NotExist; Exit; End;
IF (Errors<> [0]) Then Exit;
RemSettings(FM);
SortLines: =True;
SpecialSort: =False;
UniversalSort;
RestoreSettings(FM);
End;
Procedure Matrix. UniversalSort;
Var i,j: Integer;
Max,NMax,CZ: Integer;
Cuan: Integer;
Begin
IF Not Exist Then Begin NotExist; SortError; Exit;
End;
IF (Errors<> [0]) Then Begin SortError; Exit;
End;
IF SortLines Then Cuan: =CLines
Else Cuan: =CBars;
For i: =1 to Cuan do
Begin
IF SortLines Then Max: =CuanZeeroInLine(i)
Else Max: =CuanZeeroInBar(i);
Nmax: =i;
For j: =i to Cuan do
Begin
IF SortLines Then CZ: =CuanZeeroInLine(j)
Else CZ: =CuanZeeroInBar(j);
IF (CZ<Max) xor Direction
Then
Begin
Max: =CZ;
NMax: =j;
End;
End;
IF i<>NMax Then
Begin
IF SortLInes Then SwapLines(i,NMax)
Else SwapBars(i,NMax);
Inc(Chek);
End;
End;
End;
Function Matrix. DetWithGauss: TOE;
Var i,j: Integer;
K: TOE;
P: TOE;
S: Matrix;
Si,Sj: Integer;
Procedure SortLinesOfTheBar(B1: Integer);
Var i: Integer;
Max: TOE;
nMax: Integer;
Begin
Max: =S. GetE(1,B1);
nMax: =1;
For i: =2 to S. Clines do
IF Abs(Max) <Abs(S. GetE(i,B1))
Then
Begin
Max: =S. GetE(i,B1);
nMAx: =i;
End;
IF S. Clines<>nMAx Then
Begin
S. SwapLines(S. Clines,nMAx);
Inc(S. Chek);
End;
End;
Procedure AddLines(l1,l2: Integer; K: TOE);
Var i: Integer;
Begin
For i: =1 to S. CBars do
S. SetE(l2, i,(S. GetE(l2, i) - S. GetE(l1, i)
*K));
End;
Procedure InitObject;
Var i,j: Integer;
Ver: TOE;
Begin
Si: =0;
Sj: =0;
For i: =1 to CLines do IF not (i in Lin) Then
Inc(Si);
For j: =1 to CBars do IF not (j in Bar) Then
Inc(sj);
S. VMT;
S. DataInit(Si,Sj);
Si: =0;
For i: =1 to CLines do
IF not (i in Lin) Then
Begin
Inc(Si);
Sj: =0;
For j: =1 to CBars do
IF not (j in Bar) Then
Begin
Inc(sj);
Ver: =GetE(i,j);
S. SetE(Si,Sj,Ver);
End
End;
End;
Begin
IF Not Exist Then Begin NotExist; DGaussError;
Exit; End;
IF (Errors<> [0]) Then Begin DGaussError;
Exit; End;
IF CBars<>CLines Then Begin MNotSquare; DGaussError;
Exit; End;
InitObject;
IF S. CBars<>S. CLines Then Begin
MNotSquare; DGaussError; Exit; End;
For i: =Si downto 2 do
Begin
S. Clines: =i;
SortLinesOfTheBar(i);
S. Clines: =Si;
IF S. GetE(i, i) =0 Then Begin DetWithGauss: =0;
Exit; End;
For j: =i-1 downto 1 do
IF S. GetE(j, i) <>0 Then
Begin
K: =S. GetE(j, i) /S. GetE(i, i);
AddLines(i,j,K);
End;
End;
P: =1;
S. Clines: =Si;
S. CBars: =Sj;
For i: =1 to S. Clines do
P: =P*S. GetE(i, i);
DetWithGauss: =P*S. Sign(S. Chek);
S. Del;
End;
Function Matrix. Sign;
Begin
IF (C div 2) *2=C Then Sign: =1.0 Else
Sign: =-1.0;
End;
Procedure Matrix. SpecialSortLines;
VAr FM: Mem;
Begin
IF Not Exist Then Begin NotExist; Exit; End;
IF (Errors<> [0]) Then Exit;
RemSettings(FM);
SpecialSort: =True;
SortLines: =True;
UniversalSort;
RestoreSettings(FM);
End;
Procedure Matrix. SpecialSortBars;
VAr FM: Mem;
Begin
IF Not Exist Then Begin NotExist; Exit; End;
IF (Errors<> [0]) Then Exit;
RemSettings(FM);
SpecialSort: =True;
SortLines: =False;
UniversalSort;
RestoreSettings(FM);
End;
Procedure RemSettings;
Begin
End;
Procedure MAtrix. MNotSquare;
Begin
Errors: =Errors+ [CMNotSquare] ;
AnyError
End;
Procedure Matrix. AddError;
Begin
Errors: =Errors+ [CAddError] ;
AnyError
End;
Procedure Matrix. ReversError;
Begin
Errors: =Errors+ [CReversError] ;
AnyError
End;
Procedure Matrix. MDegenerate;
Begin
Errors: =Errors+ [CMDegenerate] ;
AnyError
End;
Procedure Matrix. Stopped;
Begin
Errors: =Errors+ [CStopped] ;
AnyError
End;
Procedure Matrix. StepRevers;
Begin
End;
Procedure Matrix. RemSettings;
Begin
With FM do
Begin
mPlus: = Plus;
mDirection: = Direction;
mSortLines: = SortLines;
mBeginZeero: = BeginZeero;
mSpecialSort: = SpecialSort;
mGauss: = Gauss;
mDetForRev: = DetForRev;
End
End;
Procedure Matrix. RestoreSettings;
Begin
With FM do
Begin
Plus: = mPlus;
Direction: = mDirection;
SortLines: = mSortLines;
BeginZeero: = mBeginZeero;
SpecialSort: = mSpecialSort;
Gauss: = mGauss;
DetForRev: = mDetForRev;
End;
End;
{********************************Quick metods
*****************************}
Function Matrix31. DetWithGauss;
Var i,j: Integer;
K: TOE;
P: TOE;
S: Matrix31;
si,sj: Integer;
Procedure SortLinesOfTheBar(B1: Integer);
Var i: Integer;
Max: TOE;
nMax: Integer;
Begin
Max: =Ar31(S. M^) [1,B1] ;
nMax: =1;
For i: =2 to S. Clines do
IF Abs(Max) <Abs(Ar31(S. M^) [i,B1])
Then
Begin
Max: =Ar31(S. M^) [i,B1] ;
nMAx: =i;
End;
IF S. Clines<>nMAx Then
Begin
S. SwapLines(S. Clines,nMAx);
Inc(S. Chek);
End;
End;
Procedure AddLines(l1,l2: Integer; K: TOE);
Var i: Integer;
Begin
For i: =1 to S. CBars do
Begin
Ar31(S. M^) [l2, i]: =Ar31(S. M^) [l2, i] -Ar31(S.
M^) [l1, i] *K;
End;
End;
Procedure InitObject;
Var i,j: Integer;
Ver: TOE;
Begin
S. VMT;
S. DataInit(31,31);
Si: =0;
IF DetForRev
Then
Begin
si: =31;
sj: =31;
Ar31(S. M^): =Ar31(M^)
End
Else
For i: =1 to CLines do
IF not (i in Lin) Then
Begin
Inc(Si);
Sj: =0;
For j: =1 to CBars do
IF not (j in Bar) Then
Begin
Inc(sj);
Ar31(S. M^) [Si,Sj]: =Ar31(M^) [i,j] ;
End
End;
End;
Begin
IF Not Exist Then Begin NotExist; DGaussError;
Exit; End;
IF (Errors<> [0]) Then Begin DGaussError;
Exit; End;
IF CBars<>CLines Then Begin MNotSquare; DGaussError;
Exit; End;
InitObject;
S. Clines: =si;
S. CBars: =sj;
IF S. CBars<>S. CLines Then Begin
MNotSquare; DGaussError; Exit; End;
For i: =si downto 2 do
Begin
S. Clines: =i;
SortLinesOfTheBar(i);
S. Clines: =si;
IF Ar31(S. M^) [i, i] =0 Then Begin
DetWithGauss: =0; Exit; End;
For j: =i-1 downto 1 do
IF Ar31(S. M^) [j, i] <>0 Then
Begin
K: =Ar31(S. M^) [j, i] /Ar31(S. M^) [i, i] ;
AddLines(i,j,K);
End;
End;
P: =1;
S. Clines: =si;
S. CBars: =sj;
For i: =1 to S. Clines do
P: =P*Ar31(S. M^) [i, i] ;
DetWithGauss: =P*S. Sign(S. Chek);
S. Del;
End;
Procedure Matrix31. SwapLines(L1,L2: Integer);
Var Prom: TOE;
i: Integer;
Begin
IF Not Exist Then BEgin NotExist; SwapError; Exit;
End;
IF (Errors<> [0]) Then Begin SwapError; Exit;
End;
For i: =1 to CBars do
Begin
Prom: =Ar31(M^) [L1, i] ;
Ar31(M^) [L1, i]: =Ar31(M^) [L2, i] ;
Ar31(M^) [L2, i]: =Prom
End;
End;
{-------------------------------------------------------------------------}
Function Matrix63. DetWithGauss;
Var i,j: Integer;
K: TOE;
P: TOE;
S: Matrix63;
si,sj: Integer;
Procedure SortLinesOfTheBar(B1: Integer);
Var i: Integer;
Max: TOE;
nMax: Integer;
Begin
Max: =Ar63(S. M^) [1,B1] ;
nMax: =1;
For i: =2 to S. Clines do
IF Abs(Max) <Abs(Ar63(S. M^) [i,B1])
Then
Begin
Max: =Ar63(S. M^) [i,B1] ;
nMAx: =i;
End;
IF S. Clines<>nMAx Then
Begin
S. SwapLines(S. Clines,nMAx);
Inc(S. Chek);
End;
End;
Procedure AddLines(l1,l2: Integer; K: TOE);
Var i: Integer;
Begin
For i: =1 to S. CBars do
Begin
Ar63(S. M^) [l2, i]: =Ar63(S. M^) [l2, i] -Ar63(S.
M^) [l1, i] *K;
End;
End;
Procedure InitObject;
Var i,j: Integer;
Ver: TOE;
Begin
S. VMT;
S. DataInit(63,63);
Si: =0;
IF DetForRev
Then
Begin
si: =63;
sj: =63;
Ar63(S. M^): =Ar63(M^)
End
Else
For i: =1 to CLines do
IF not (i in Lin) Then
Begin
Inc(Si);
Sj: =0;
For j: =1 to CBars do
IF not (j in Bar) Then
Begin
Inc(sj);
Ar63(S. M^) [Si,Sj]: =Ar63(M^) [i,j] ;
End
End;
End;
Begin
IF Not Exist Then Begin NotExist; DGaussError;
Exit; End;
IF (Errors<> [0]) Then Begin DGaussError;
Exit; End;
IF CBars<>CLines Then Begin MNotSquare; DGaussError;
Exit; End;
InitObject;
S. Clines: =si;
S. CBars: =sj;
IF S. CBars<>S. CLines Then Begin
MNotSquare; DGaussError; Exit; End;
For i: =si downto 2 do
Begin
S. Clines: =i;
SortLinesOfTheBar(i);
S. Clines: =si;
IF Ar63(S. M^) [i, i] =0 Then Begin
DetWithGauss: =0; Exit; End;
For j: =i-1 downto 1 do
IF Ar63(S. M^) [j, i] <>0 Then
Begin
K: =Ar63(S. M^) [j, i] /Ar63(S. M^) [i, i] ;
AddLines(i,j,K);
End;
End;
P: =1;
S. Clines: =si;
S. CBars: =sj;
For i: =1 to S. Clines do
P: =P*Ar63(S. M^) [i, i] ;
DetWithGauss: =P*S. Sign(S. Chek);
S. Del;
End;
Procedure Matrix63. SwapLines(L1,L2: Integer);
Var Prom: TOE;
i: Integer;
Begin
For i: =1 to CBars do
Begin
Prom: =Ar63(M^) [L1, i] ;
Ar63(M^) [L1, i]: =Ar63(M^) [L2, i] ;
Ar63(M^) [L2, i]: =Prom
End;
End;
END.
Контрольні приклади
Дана матриця:
 3
- 1 0 3
- 1 0
А= - 2 1 1
2 - 1 4
Відповідь:
1 0,8 - 0,2
А-1 = 2 2,4 - 0,6
0 0,2 0,2
Квадратна матриця називається виродженою (для
особливої), якщо її визначник дорівнює нулю, і невиродженою (чи неособливої) - у
протилежному випадку. Відповідно лінійне перетворення невідомих називається
виродженим чи невиродженим у залежності від того, чи буде дорівнює чи нулю
відмінний від нуля визначник з коефіцієнтів цього приобразования. З теореми
випливає наступне твердження:
Добуток матриць, хоча б одна з яких вироджена,
буде вродженою матрицею.
Добуток будь-яких невироджених матриць саме
буде невирожденою матрицею. Звідси випливає, через зв'язок, що існує між
множенням матриць і послідовним виконанням лінійних перетворень, таке
твердження: результат послідовного виконання декількох лінійних перетворень
тоді і тільки тоді буде невиродженим перетворенням, якщо всі задані
перетворення невироджені.
1. А.Г. Курош «курс высшей
алгебры», «наука», Москва 1975
2.С.Т. Завало, В.М. Костарчук,
Б.И. Хацет «алгебра и теория чисел», Том 1,«высшая школа», Киев 1974
3. С.Т. Завало, В.М. Костарчук,
Б.И. Хацет «алгебра и теория чисел», Том 2, «высшая школа», Киев 1976
|