Курсовая работа: Turbo Pascal
Курсовая работа: Turbo Pascal
Рязанская
государственная радиотехническая академия
Кафедра
Вычислительной и Прикладной математики
Пояснительная записка
К курсовой работе
по дисциплине
«Алгоритмические
языки и программирование»
Рязань 2006
Содержание
Задание на курсовую работу.
Введение.
1.
Анализ задания и
математическая постановка задачи.
2.
Разработка схемы алгоритма
и её описание.
3.
Инструкция по
использованию разработанной программы.
4.
Проверка
правильности функционирования программы.
5.
Текст программы и
её описание.
Список литературы.
РЯЗАНСКАЯ
РАДИОТЕХНИЧЕСКАЯ АКАДЕМИЯ
ФАКУЛЬТЕТ
ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
КАФЕДРА
ВЫЧИСЛИТЕЛЬНОЙ И ПРИКЛАДНОЙ МАТЕМАТИКИ
Задание
на курсовую работу по
дисциплине
«Алгоритмические языки и
программирование»
Студенту Хамидулину А.Р.
группы 041.
Задание 1. Составить программу вычисления
матрицы P=f(A,B,C)
f(A,B,C) – матричное выражение. A,B,C – исходные
матрицы,
Размер и значение
элементов, которых набираются произвольно.
f(A,B,C)=C(A+2B)T.
Сформировать вектор из
средних арифметических значений элементов столбцов.
Задание 2. Составить программу вычисления
определённого интеграла 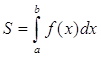 с
погрешностью, не превышающей заданную величину ε. Для проверки программы
интегрирования вычислить с
погрешностью, не превышающей заданную величину ε. Для проверки программы
интегрирования вычислить 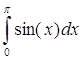 определённый
интеграл с заданной точностью. определённый
интеграл с заданной точностью.
Интеграл вычислить с помощью
формулы прямоугольников.
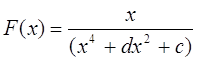
Пределы интегрирования: a=1; b=2.
Значения коэффициентов:
c= 1,9; 2,05; 2,1; 2,2.
d= 3; 3,05; 3,1.
Погрешность ε: 10-4.
Дата выдачи
задания:
Дата
выполнения задания:
Преподаватель:
Баринов В.В.
Введение
Современные средства
вычислительной техники и ЭВМ позволяют существенным образом повысить
эффективность деятельности инженеров при решении различных задач. При этом
наиболее существенным вопросом является организация взаимодействия пользователя
со средствами ЭВМ. В настоящей курсовой работе для этих целей использовался
диалоговый режим, что позволило существенным образом упростить процесс отладки
и работы с программой. В качестве языка программирования выбран изучаемый на
занятиях по дисциплине «Алгоритмические языки и программирование» язык
программирования «Паскаль». К достоинствам языка следует отнести такие его
характеристики, как модульность, универсальность, удобство работы с массивами и
т. д.
Задание 1
1.
Анализ задания и
математическая постановка задачи
При
решении поставленной задачи необходимо выполнить следующие действия:
1.
Ввести значения
элементов матриц A, B, C.
2.
Напечатать
значения элементов исходных матриц.
3.
Провести
транспонирование матрицы B, т.
е. вычислить матрицу U=BT.
4.
Умножить матрицу ВТ
на 2, т. е. вычислить матрицу U=2*ВТ.
5.
Сложить матрицы A и 2*ВТ, т. е. вычислить
матрицу U=A+2*ВТ.
6.
Умножить матрицы С
и (A+2*BТ), т. е. вычислить матрицу
U=C*(A+2*BT).
7.
Вывести матрицу U.
8.
Сформировать
вектор VECT из средних арифметических значений
элементов столбцов.
9.
Вывести вектор VECT .
Печать целесообразно
реализовать с помощью подпрограммы (процедуры общего вида). Пункты 1-8
целесообразно также оформить в виде подпрограмм.
Матрицей будем называть
таблицу чисел:
А11 А12 … А1N
A21
A22 … A2N
- - - - - - -
- -
AM1
AM2 … AMN
Если m=n, то матрица
называется квадратной, n-порядок.
Произведением 2-х
прямоугольных матриц
А11 А12 …
А1N
A=A21
A22 … A2N
- - - - - - -
- -
AM1
AM2 … AMN
B11 B12
… B1N
B=B21
B22 … B2N
- - - - - - - - -
BM1 BM2 … BMN
называется матрица
C11 C12 … C1N
C=C21
C22 … C2N
- - - - - - -
- -
CM1
CM2 … CMN
у которой элемент Сij, стоящий на пересечении i-ой строки и j-ого столбца, равен сумме произведений соответствующих
элементов i-ой строки первой матрицы А и j-того столбца 2-ой матрицы В.
Суммой 2-х прямоугольных
матриц А=(аi j) и В=(вi j) одинаковых размеров (m х n) называется матрица С=(сi j) тех же размеров, элементы которой равны суммам cответствующих элементов данной
матрицы.
2.Разработка
схемы алгоритма и её описание
По результатам анализа
задания можно составить укрупненную схему алгоритма последовательной структуры:

Проведём детализацию блоков.
1) Подпрограмма ввода матриц.
Имя подпрограммы : inputm.
2) Подпрограмма вывода матриц.
Имя подпрограммы : outputmat.

3) Подпрограмма
транспонирования матриц
 Имя подпрограммы transpm. Имя подпрограммы transpm.
4) Подпрограмма умножения
матриц
Имя подпрограммы : multm.
5) Подпрограмма умножения
матрицы на число
Имя подпрограммы : multconstm.
 6) Подпрограмма сложения матриц 6) Подпрограмма сложения матриц
Имя подпрограммы : sum_m.
7) Подпрограмма формирования
вектора из средних арифметических значений элементов столбцов.
Имя подпрограммы : sred_arifm.
Полный алгоритм решения
задачи.

3. Инструкция
по использованию разработанной программы
Определим исходные
данные.
Матрица А: Матрица В: Матрица
С:
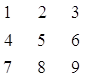 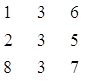 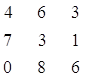
Описание переменных и
массивов:
| Исходные сведения |
Описание в программе |
| Обозначение |
Назначение |
Идентификатор,
размерность
|
Атрибуты |
| i, j, k |
Индексные переменные |
i, j, k |
Integer |
| n |
Размерность
матриц
|
n |
Word |
|
A, B, C,
U, Vect
|
Матрицы
исходных данных и результата
|
a(10,10),
b(10,10), c(10,10), u(10,10),
vect(10)
|
Array of real |
| a, b, c, z |
Матрицы, используемые в подпрограммах |
a(10,10), b(10,10),
c(10,10), z(10)
|
Array of real |
| R,S |
Переменная, используемая в подпрограмме |
r |
Real |
| m |
Переменная, используемая в подпрограмме |
m |
Char |
|
|
|
|
|
4. Проверка
правильности функционирования программы.
Введём исходные данные.
Программа выводит для
контроля входные данные:
Матрица А: Матрица В: Матрица
С:
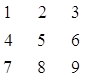 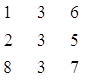 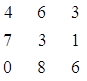
Вывод результирующей
матрицы:
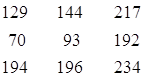
Вывод матрицы
Vect:
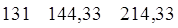
5.Текст
программы и её описание.
В процессе получения
результирующей матрицы реализованы следующие действия с массивами:
-транспонирование
квадратных матриц произвольной размерности;
-умножение квадратных
матриц произвольной размерности;
-сложение квадратных
матриц произвольной размерности;
-умножение на число
квадратных матриц произвольной размерности;
Все указанные действия
реализованы с помощью подпрограмм. Ввод и вывод матриц также реализован в подпрограммах.
Окончательный
вариант программы:
Модуль
KursUn,содержащий описанные
подпрограммы.
Unit KursUn;
{*** Начало модуля KursUn
***}
interface
{*** Интерфейсная секция ***}
uses
crt;
type
matrix= array [1..10,1..10] of real;
vector= array [1..10] of real;
var
i,j,k:integer;
n:word;
procedure outputmat (n:word; a:matrix; m:char);
procedure inputm (n:word; var a:matrix;m:char);
procedure sred_arifm (n:word; a:matrix;var
z:vector);
procedure transpm (n:word; a:matrix; var c:matrix);
procedure sum_m (n:word; a,b:matrix; var c:matrix);
procedure multm (n:word; a,b:matrix; var c:matrix);
procedure multconstm (n:word; r:real; a:matrix;var
c:matrix);
implementation {*** ИСПОЛНЯЕМАЯ
ЧАСТЬ
***}
{***************************************************************************}
{*** процедура
ввода
матриц
***}
procedure inputm;
begin
clrscr;
writeln;
writeln(' Введите матрицу ',m,'
размером ',n,'*',n);
for
i:=1 to n do
for j:=1 to n do
begin
write(' ',m,'[',i,',',j,']=');
readln(a[i,j]);
end;
end;
{***************************************************************************}
{*** процедура
вывода
матриц
***}
procedure outputmat;
begin
writeln;
writeln(' Матрица
',m,'.');
writeln;
for i:=1 to n do
begin
write(' ');
for j:=1 to n do
write(' ',a[i,j]:3:1);
writeln;
end;
end;
{***************************************************************************}
{***
процедура транспонирования матрицы ***}
procedure
transpm;
begin
for i:=1 to n do
for j:=1 to n do
c[j,i]:=a[i,j];
end;
{***************************************************************************}
{***
процедура умножения матрицы на число ***}
procedure
multconstm;
begin
for i:=1 to n do
for j:=1 to n do
c[i,j]:=a[i,j]*r
end;
{***************************************************************************}
{***
процедура суммирования матриц ***}
procedure
sum_m;
begin
for i:=1 to n do
for j:=1 to n do
c[i,j]:=a[i,j]+b[i,j];
end;
{***************************************************************************}
{*** процедура
умножения
матриц
***}
procedure multm;
begin
for i:=1 to n do
for j:=1 to n do
begin
c[i,j]:=0;
for k:=1 to n do
c[i,j]:=c[i,j]+a[i,k]*b[k,j];
end;
end;
{***************************************************************************}
{***
процедура формирования вектора из средних ***}
{***
арифметических значений элементов столбцов ***}
procedure
sred_arifm;
var
S:real;
begin
S:=0;
for i:=1 to n do
begin
for j:=1 to n do
S:=S+a[j,i];
z[i]:=S/n;
S:=0;
end;
end;
{***************************************************************************}
end.
{*** Конец модуля KursUn
***}
Основная
программа.
Program Kursach1;
Uses KursUn , Crt;
Var
a,b,c,u : matrix;
vect : vector;
begin
ClrScr; textcolor(LightCyan);
writeln;
writeln(' ╔═══════════════════════════════════════════════════════════════╗');
writeln(' ║ Эта
программа
вычисляет
матричное
выражение
║');
writeln(' ║ ║');
writeln(' ║ T ║');
writeln(' ║ U=C*( A+2*B ) ║');
writeln(' ║ ║');
writeln(' ╚═══════════════════════════════════════════════════════════════╝');
writeln;
write('
Введите размерности матриц: '); readln(n);
if
n=0 then {*** проверка размерности матрицы ***}
begin
ClrScr; textcolor(red);
writeln;
writeln(' Такая размерность не
допустима!!!');
readkey;
exit;
end;
ClrScr;
inputm(n,a,'A'); {*** ввод
матрицы
A ***}
ClrScr;
inputm(n,b,'B'); {*** ввод
матрицы
B ***}
ClrScr;
inputm(n,c,'C'); {*** ввод
матрицы
C ***}
transpm(n,b,u); {*** транспонирование
матрицы B. ***}
multconstm(n,2,u,u);
{*** умножения матрицы на 2. ***}
sum_m(n,a,u,u);
{*** суммирование матриц A+2*BT. ***} multm(n,c,u,u); {*** умножение матриц С и
(A+2*BT). ***}
ClrScr;
writeln;
writeln('
****************** Исходные значения ********************');
outputmat(n,
a, 'A');
{*** вывод матрицы A
***}
outputmat(n,
b, 'B');
{*** вывод матрицы B
***}
outputmat(n,
c, 'C');
{*** вывод матрицы C
***}
writeln;
writeln('
***** Для продолжения нажмите любую клавишу *****');
readkey;
outputmat(n,
u, 'U'); {*** вывод результата: матрицы U ***}
writeln;
writeln('
***** Для продолжения нажмите любую клавишу *****');
readkey;
ClrScr;
writeln;
writeln(' *******************************************************');
writeln(' * Вектор из средних
арифметических значений элементов *');
writeln('
* столбцов результирующей матрицы. *');
writeln(' *******************************************************');
sred_arifm(n, u, vect);
writeln; write(' ');
for i:=1 to n do
write(' ',vect[i]:5:2);
writeln;
readkey;
end.
Задание 2
1.
Анализ задания и
математическая постановка задачи
При решении поставленной
задачи необходимо выполнить следующие действия:
1.
Ввод исходных
данных.
2.
Нахождение
значения определённого интеграла с использованием метода прямоугольников.
3.
Вывод
результатов.
При численном
интегрировании вместо кривой подынтегральной функции используют заменяющие
(аппроксимирующие) её кривые или ломаные линии, для которых вычисление
ограниченной ими площади производится в соответствии с достаточно несложными
формулами.
Принцип метода
прямоугольников состоит в том, что исходный отрезок разбивается на достаточно
малые части:
a= x1< x2<
x3<…< xn-1< xn=b; h= xk-xk-1;
площадь каждой такой
части (прямоугольника): Sk=h*f(xk);
соответственно площадь
всей фигуры, образованной из n-1
таких прямоугольников: S= S1+S2+…+ Sn-2+ Sn-1.Величина S является приближённым значением определённого интеграла, она
приближается к истинному значению при увеличении числа n.
Погрешность данного
метода определяется абсолютным значением разности приближённых значений
определённого интеграла при различных n. Если эта разность меньше требуемой погрешности, то необходимая точность
достигнута, и дальнейшее увеличение n не требуется.
2. Разработка
схемы алгоритма и её описание
По результатам анализа
задания можно составить укрупненную схему алгоритма последовательной структуры:
Полный алгоритм:
|
|
|
h:= (b-a)/n; y1:=y2;
y2:=0; x:=a+h;
|
|
 Нет Нет
|




Инструкция по
использованию разработанной программы
Определим исходные
данные.
a=1;
b=2; e=0.0001;
c= 1,9; 2,05; 2,1; 2,2.
d= 3; 3,05; 3,1.
| Исходные сведения |
Описание в программе |
| Обозначение |
Назначение |
Идентификатор |
Атрибуты |
| A, B |
Пределы интегрирования |
a, b |
Real |
| C,D |
Параметры |
c, d |
Real |
| e |
Погрешность |
eps |
Real |
| y1, y2 |
Значения определённого интеграла при числах разбиений n и 2*n |
y1, y2 |
Real |
| h |
Шаг интегрирования (определяется по формуле h=(b-a)/n) |
h |
Real |
| x |
Текущее значение аргумента |
x |
Real |
| n |
Количество разбиений отрезка [a;b] |
n |
Longint |
Описание переменных и
массивов:
4. Проверка
правильности функционирования программы.
Введём определённые ранее
исходные данные.
a=1; b=2; e=0.0001;
c=1,9; d=3;
При c=1,90 и d=3,00 значение определённого интеграла
0,113 с точностью до 0,00010
Количество разбиений отрезка
[1,00;2,00]: 4000
c=2,05; d=3,05
При c=2,05 и d=3,05 значение определённого интеграла
0,110 с точностью до 0,00010
Количество разбиений отрезка
[1,00;2,00]: 4000
c=2,2; d=3,1
При c=2,20 и d=3,10 значение определённого интеграла
0,108 с точностью до 0,00010
Количество разбиений отрезка
[0,00;2,00]: 4000
Для проверки программы
интегрирования вычислим определённый интеграл 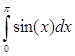 с
заданной точностью. с
заданной точностью.
a=0; b=3.14;
eps=0.0001.
Определённый интеграл 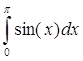 =2. =2.
5.Текст программы
Program kursach2;
uses crt;
var
a,b,c,d,e,y1,y2,h,x:real;
n:longint;
begin
clrscr; textcolor(11);
writeln(' ╔═══════════════════════════════════════════════════════════════╗');
writeln(' ║ Эта
программа
вычисляет
определённый
интеграл
от
функции
║');
writeln(' ║ ║');
writeln(' ║ x ║');
writeln(' ║ f(x)= ------------- ║');
writeln(' ║ (x^4+d*x^2+c) ║');
writeln(' ║ ║');
writeln(' ║ на
отрезке
[a,b] с
погрешностью
e. ║');
writeln(' ╚═══════════════════════════════════════════════════════════════╝');
writeln;
write(' Введите
левую
границу
интервала:
'); readln(a);
write(' Введите правую границу интервала:
'); readln(b);
write('
Введите погрешность вычислений: '); readln(e);
clrscr;
writeln('
*****************************************');
write('
Введите значения c: '); read(c);
write('
Введите значения d: '); read(d);
n:=2000;
y2:=0;
repeat
h:=(b-a)/n; y1:=y2;
y2:=0; x:=a+h;
repeat
y2:=y2+h*x/(x*x*x*x+d*x*x+c);
{y2:=y2+h*sin(x);}
x:=x+h;
until x>b;
n:=2*n;
if n>255000 then
begin
ClrScr; textcolor(red); writeln;
writeln(' **** Сработала защита от
зацикливания ****');
readkey;
exit;
end;
until abs(y1-y2)<e;
ClrScr;
writeln;
writeln('*******************************************************************');
writeln('При с=',c:3:2,'и
d=',d:3:2,'значение определённого интеграла',y2:5:3);
writeln('
с точностью до ',e:6:5 );
writeln;
writeln('
Количество разбиений отрезка [',a:3:2,';',b:3:2,']: ',n div 2 );
writeln('*******************************************************************');
readkey;
end.
Список литературы
1. Методические указания по выполнению курсовой работы «Алгоритмические
языки и программирование»
№1525, Рязань: РРТИ, 1988.
2. Методические указания «Модульное программирование на Турбо
Паскале» №3037,В.С.Новичков, Н. И. Парфилова, А. Н. Пылькин, Рязань: РГРТА,
2000.
3. «Программирование на языке ПАСКАЛЬ», Г. Л. Семашко, А. И.
Салтыков, Москва «Наука», 1988.
4. «Программирование на языке
ПАСКАЛЬ», О. Н. Перминов, «Радио и связь», 1988.
|