Курсовая работа: Рішення систем нелінійних рівнянь. Метод ітерацій. Метод Ньютона–Канторовича
Курсовая работа: Рішення систем нелінійних рівнянь. Метод ітерацій. Метод Ньютона–Канторовича
ОБЛАСНИЙ КОМУНАЛЬНИЙ
ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД "ІНСТИТУТ ПІДПРИЄМНИЦТВА "СТРАТЕГІЯ"
КАФЕДРА ЕКОНОМІЧНОЇ
КІБЕРНЕТИКИ
Курсова робота
З дисципліни: "Обчислювальні
методи"
На тему: "Рішення
систем нелінійних рівнянь. Метод ітерацій. Метод Ньютона - Канторовича."
Студента Іощенка І.Г.
группа С-05-51
Керівник Андрейшина Н.Б.
Філімоненко М.І.
м. Жовті Води 2007
Зміст
Вступ
1. Рішення систем
нелінійних рівнянь
1.1 Метод ітерацій
1.1.1 Приклад рішення
системи нелінійних рівнянь методом ітерацій
1.2 Метод найшвидшого
спуску
1.2.1 Приклад рішення
системи нелінійних рівнянь методом спуска
1.3 Метод
Ньютона-Канторовича
При рішенні систем нелінійних і трансцендентних рівнянь дуже складно
знайти точне рішення, тому точним рішення рівняння не є. Задача пошуку кореня
системи рівняння може вважатися практично вирішеною, якщо ми зуміємо визначити
корінь з потрібним ступенем точності і вказати межі можливої погрішності. Умови
збіжності метода Ньютона для системи досліджувалися Виллерсом, Стениним,
Канторовичем.
У наш час рішення систем нелінійних рівнянь досить актуальна тема, адже
її можна застосовувати на практиці для рішення кола задач. Прикладом цього є
задачі, які виникають у геодезії.
Цілю моєї курсової роботи є опис методів рішення систем нелінійних
рівнянь, а також продемонструвати на практиці рішення системи рівнянь методом
Ньютона - Канторовича та написання програми до цього методу.
Задачі, які виникають при математичній обробці результатів вимірювання,
як правило, зводяться до рішення нелінійних систем алгебраїчних або
трансцендентних рівнянь:
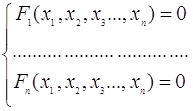
або у векторній формі
F (X) = 0.
Як і у випадку одного рівняння, рішення нелінійних систем рівнянь
поділяється на два етапи:
знаходження приблизного рішення системи;
уточнення приблизного рішення.
Для знаходження приблизного значення коренів системи рівнянь не існує
загальних методів. Завжди кожна нелінійна система повинна розглядатися як спеціальна
задача.
Для уточнення коренів розробленні загальні методи. Найбільш
розповсюдженні в нинішній час є метод ітерацій, метод спуска, метод Ньютона та
деякі їх модифікації.
Нехай дана система нелінійних рівнянь спеціального виду
 (1) (1)
де функції  , , 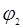 ,... ., ,... ., 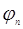 дійсно визначенні та непереривні
на деякій області дійсно визначенні та непереривні
на деякій області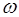 ізольованого
рішення ізольованого
рішення 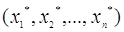 цієї системи. цієї системи.
Розглядаючи вектори 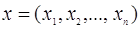 і і 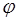 (x) = ( (x) = (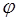 1 (x), 1 (x),  2 (x), …. ., 2 (x), …. .,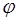 n (x)), систему
(1) можна записати у виді: n (x)), систему
(1) можна записати у виді:
x = 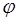 (x) (2) (x) (2)
Наприклад, для рішення системи двох нелінійних рівнянь з двома
невідомими
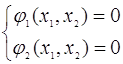
потрібно перейти до рівностей:
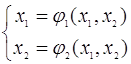
Нехай вибрано початкове приближення (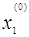 , ,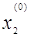 ), тоді ), тоді
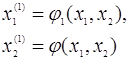
і k+1 приближення буде розраховуватися за формулами
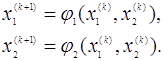
Відомо, що процес ітерації зводиться до рішення системи, якщо усі числа
матриці
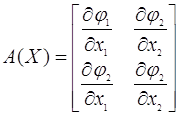
по модулю менше одиниці. Більш простою вимогою, використовуваною на
практиці, є наступне: сума модулів частних похідних по кожному стовбці матриці
повинна бути менша одиниці
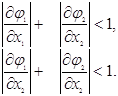
У випадку використання методу ітерацій до системи n рівнянь, k+1
ітерація буде будуватися по формулам
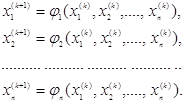
Тоді вимога сходження матиме вигляд:

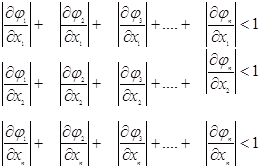
Слід відмітити, що ця вимога виповняється для дуже малого числа
функцій, і тому метод ітерації дуже рідко використовується на практиці, не
дивлячись на його простоту.
Рішить систему рівнянь
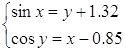
Ця система еквівалентна системі рівнянь:
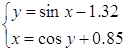
Виберемо початкові приближення 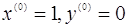 та
провіримо умови та
провіримо умови
сходження процесу. Часні похідні мають вигляд
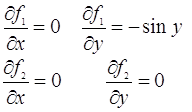
Маємо
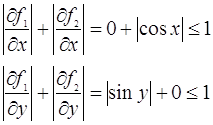
Звідси слідує, що процес сходиться. Розрахунки на правому приближенні
дають:
x (1) =1+0.85=1.85
y (1) =0.842-1.32=-0.478
x (2) =0.888+0.85=1.738
y (2) =0.961-1.32=0.359
x (3) =0.936+0.85=1.786
y (3) =0.986-1.32=0.334
x (4) =0.945+0.85=1.795
y (4) =0.977-1.32=0.343
x (5) =0.9408+0.85=1.7908
y (5) =0.9750-1.32=
- 0.3450
x (6) =0.9411+0.85=1.7911
y (6) =0.9759-1.32=0.3441
x (7) =0.9414+0.85=1.7914
y (7) =0.9758-1.32=-0.3442.
Нехай маємо систему рівнянь:
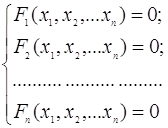
або в матричному вигляді:
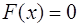
де
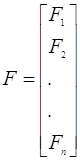
Допустимо, що функція  дійсно непереривна
та непреривно диференційована в загальній області визначення. Розглянемо
функцію дійсно непереривна
та непреривно диференційована в загальній області визначення. Розглянемо
функцію
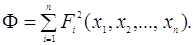
Тоді рішення даної системи зводиться до мінімізації цієї функції.
Для мінімізації по методу спуску вибирається початковий вектор Х0,
а потім шукається напрямлення спуска до рішення 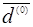 ,
таке щоб ,
таке щоб
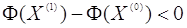
для векторів Х (1) виду 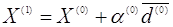 .
Тут .
Тут 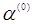 - скалярна величина, постійна
для даної ітерації і знаходить величину шагу за напрямом - скалярна величина, постійна
для даної ітерації і знаходить величину шагу за напрямом 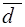 . .
Методи спуску розрізняються в залежності від вибору напрямлення спуска.
Одним із найкращих направлень є напрямлення градієнта
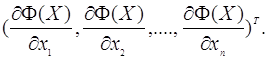
Функція Ф (Х (і)) задається в n-мірному просторі сімейства
гіперповерхонь і градієнт вирішує напрям найшвидшого спуска. Тому саме воно
використовується у методі найшвидшого спуска для мінімізації функції.
Другою проблемою в методах найшвидшого спуску є вибір величини шагу 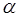 , на який потрібно про
двинутися вздовж напряму зменшення функції. , на який потрібно про
двинутися вздовж напряму зменшення функції.
Спробуємо вибрати оптимальний шаг 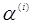 для для
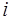 - ітерації методу
найшвидшого спуска і побудувати вектор - ітерації методу
найшвидшого спуска і побудувати вектор
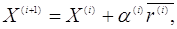
для якого функція 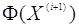 приймає
менше значення, чим приймає
менше значення, чим 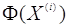 . Розкладемо
функцію . Розкладемо
функцію
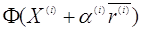
в ряд Тейлора та обмежившись членами другого порядку меншості получимо
 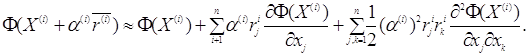 (3) (3)
 Тоді значення Тоді значення
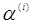 , для якого функція , для якого функція 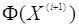 прийме мінімальне значення,
визначається із умови прийме мінімальне значення,
визначається із умови 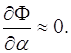 Про
диференціювавши рівняння (3) по Про
диференціювавши рівняння (3) по 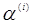 і
враховуючи, що і
враховуючи, що 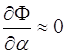 получимо получимо
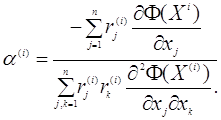 (4) (4)
Оскільки в методі найшвидшого спуску компоненти градієнта мають вигляд
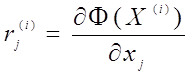
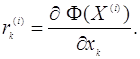
то формула (4) після підстановки цих рівнянь перейде до вигляду
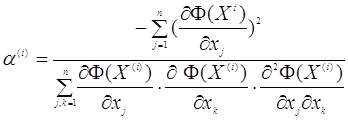 (5) (5)
Формула (5) дуже складна оскільки потребує рахування других часних похідних.
На практиці завжди використовується наступний варіант знаходження 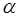 . .
Нехай значення Ф (Х) змінюється вздовж напрямку градієнта 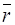 . Розглянемо точку
пересікання кривої . Розглянемо точку
пересікання кривої 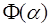 та касатільної в
точці та касатільної в
точці 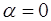 з осю з осю 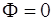 . .
Вона буде розраховуватися наступним чином:
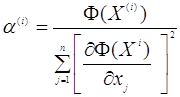 . (6) . (6)
Як бачимо, в цьому випадку 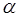 рахується
просто, але сходження метода може бути дуже повільно. Тому інколи на практиці
використовують наступну модифікацію. рахується
просто, але сходження метода може бути дуже повільно. Тому інколи на практиці
використовують наступну модифікацію.
Для кожної ітерації метода рахують значення функціонала при 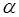 , а потім при , а потім при 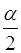 і будують квадратичне
наближення функціонала, який проходить через три точки і будують квадратичне
наближення функціонала, який проходить через три точки 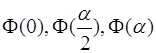 . Продиференціювавши отримане
рівняння по . Продиференціювавши отримане
рівняння по 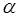 та прирівнявши похідну,
получимо наступне рівняння для та прирівнявши похідну,
получимо наступне рівняння для 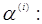
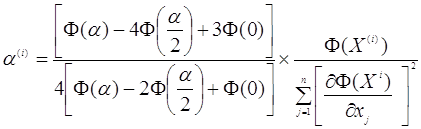 (7) (7)
Практика показує, що хоча цей варіант більш громіздкий, так як у
порівнянні з формулою (5) доводиться додатково рахувати два значення функції 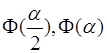 , але метод сходиться
набагато швидше. , але метод сходиться
набагато швидше.
Інколи характер Ф (Х) такий, що аналітичне рівняння для частних похідних
має надто складний вигляд і рахувати їх надто складно.
Також слід відмітити, що якщо в області шуканого рішення є локальні
мінімуми, то метод спуска може не привести до шукаємого рішення, а можуть
зійтися до одного з цих мінімумів. Практично часто спуск буває дуже повільним
навіть при відсутності локальних мінімумів.
Порядок рахування в методі найшвидшого спуска наступний:
знаходиться аналітичне рівняння для градієнта 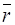 ; ;
вибирають початкове приближення вектора невідомих 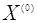 ; ;
вираховують координати градієнта 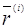 в
точці в
точці 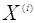 ; ;
вираховують шаг по градієнту 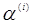 по
формулам (6) або (7); по
формулам (6) або (7);
вираховують уточнений вектор невідомих 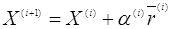 . .
Далі процес повторюється з пункту 3 до сходження.
Методом найшвидшого спуска приблизно розрахувати корені системи
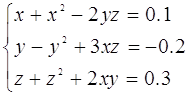
розміщенні в області початку координат.
Маємо:
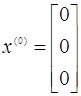 Тут Тут 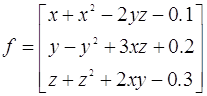 та та
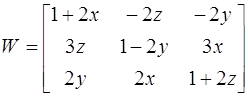
Підставляємо нульове приближення, будемо мати:
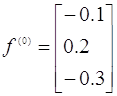 та та 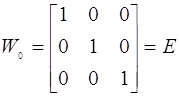
по формулам получимо перше приближення
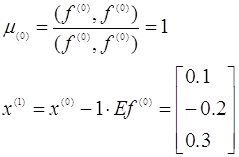
Аналогічно находимо друге приближення 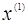 .
Маємо: .
Маємо:
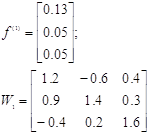
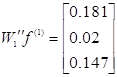
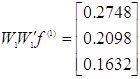 
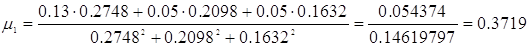
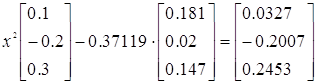
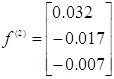 . .
Метод Ньютона-Канторовича, придатний для проведення розрахунків в Excel.
Як і в методі Ньтона для нелінійних рівнянь для знаходження кореня системи нелінійних
рівнянь необхідно спочатку якимсь чином знайти початкове наближення до цього кореня
(тобто вектор
 ), ),
а потім вже використовуються ітераційні формули методу проводиться його
уточнення до досягнення заданої точності. Виклад методу (і його використання) зручніше
проводити в матричній формі запису. При цьому, окрім векторів, 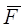 , , 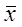 и и 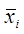 (. (i - номер ітерації,,
i ³ 0)
) використовується також матриця A (розмірності n ´ n), що складається з приватних
похідних по всіх компонентах вектора (. (i - номер ітерації,,
i ³ 0)
) використовується також матриця A (розмірності n ´ n), що складається з приватних
похідних по всіх компонентах вектора  : :
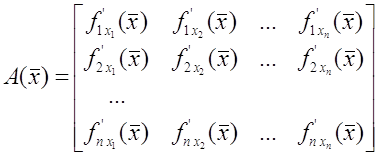 : :
Розглянемо ці методи для випадку n=2, тобто коли рівнянь в системі два і
невідомих теж дві. В цьому випадку
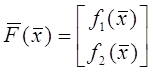 ,
та ,
та 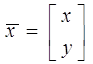 . .
Ідея методу полягає в розкладанні вектор-функції в ряд Тейлора в околиці
початкового наближення із збереженням тільки доданків першого ступеня. Позначимо
найдене (якимсь чином) початкове приближення до шуканого кореня через 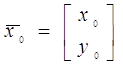 . Тоді можна приблизно записати . Тоді можна приблизно записати
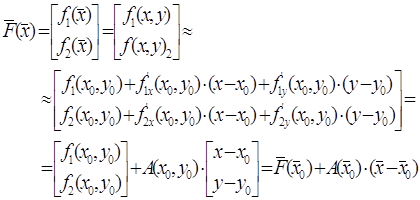 ,
(8) ,
(8)
На основі формула (8) будується ітараційна формула. А саме, 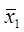 вибирається так, щоб вибирається так, щоб 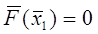 . .
Тоді (у загальному вигляді) ітераційна формула матиме вигляд
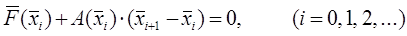 (9) (9)
В методі Ньютона цю ітераційну формулу перетворять до вигляду
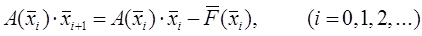 (10) (10)
У координатному вигляді формула (10) представляє систему з двох рівнянь
щодо двох невідомих xi+1 и yi+1.
У матричному вигляді рішення її матиме вигляд
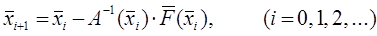
допоміжний вектор-стовпець z, що містить n елементів.
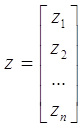 (11) (11)
Ітераційна формула методу в матричному записі має наступний вигляд
zj = - A-1 (xj) ×F
(xj)
xj +1 = xj + zj, (12)
тут j - номер ітерації,  - початкове
наближення шуканого кореня. Процес ітерацій завершується, якщо всі елементи останнього
вектора z по абсолютній величині стануть менше заданої точності (кажучи точніше,
коли норма вектора z стане менше заданої точності). - початкове
наближення шуканого кореня. Процес ітерацій завершується, якщо всі елементи останнього
вектора z по абсолютній величині стануть менше заданої точності (кажучи точніше,
коли норма вектора z стане менше заданої точності).
Обчислення даним методом зручно проводити в Excel з використанням функцій
матричної алгебри. Результати розрахунків представляються у вигляді таблиці.
Для випадку n=2 система рівнянь найчастіше має такий вигляд:
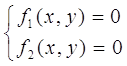
Як змінна х1 тут виступає змінна х,
а як змінна х2 - змінна y. Матриця А, вектори F і z в
цьому випадку приймуть вигляд:
А = 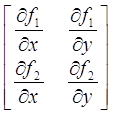 , F = , F = 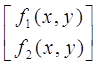 , z = , z = 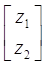 , ,
Порядок рішення системи нелінійних рівнянь методом Ньютона-Канторовича полягає
в послідовному виконанні наступних дій:
Знайти початкове (нульове) наближення х0 шуканого
кореня заданої системи рівнянь. Для випадку n=2 це можна зробити графічним методом,
побудувавши графіки кожної з функцій і приблизно визначивши координати точок перетинів
графіків. В цьому випадку вектор початкового наближення може мати вигляд 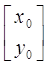 ; ;
Привести задану систему до вигляду (1), перенести все з правої частини рівняння
в ліву;
Записати в аналітичному вигляді матрицю А, використовуючи формулу (8);
Приймемо j=0;
Підставимо значення хj в аналітичні вирази для
матриці А і вектора F;
Знайдемо зворотну матрицю А-1;
По формулах (12) знайдемо вектор zj і вектор хj+1;;;
Знайдемо норму вектор zj;
Якщо норма вектора zj більше заданої точності обчислення
(норма більша за ε) - наростимо значення j на одиницю і повернемося до пункту
5 цього переліку;
За знайдене рішення приймемо останнього набутого значення вектора х.
|