Курсовая работа: Метод наближеного обчислення коренів. Програма
Курсовая работа: Метод наближеного обчислення коренів. Програма
Міністерство
освіти і науки України
ФАКУЛЬТЕТ
ІНФОРМАТИКИ
КАФЕДРА
ІНФОРМАЦІЙНИХ УПРАВЛЯЮЧИХ СИСТЕМ ТА ТЕХНОЛОГІЙ
Реєстраційний
№________
Дата
___________________
КУРСОВА
РОБОТА
Тема:
Метод
наближеного обчислення коренів. Програма.
Рекомендована
до захисту
“____”
__________ 2008р.
Робота
захищена
“____”
__________ 2008р.
з
оцінкою
_____________________
Підписи
членів комісії
Зміст
Вступ
Теоретична частина
1. Межі дійсних коренів
2. Число дійсних коренів
Практична частина
1. Опис програми
2. Текст програми
Контрольні приклади
Висновок
Література
Вступ
Не існує методу
для пошуку точних значень многочленів з числовими коефіцієнтами. Адже, деякі
проблеми механіки, фізики і інших галузей техніки зводиться до питання про
корені многочленів, іноді досить високим степенем. Ця обставина з’явилася
приводом для численних досліджень, що мали метою навчитися робити ті чи інші
висловлення про корені многочлена з числовими коефіцієнтами, не знаючи цих
коренів. Для многочленів з дійсними коефіцієнтами розроблялися методи
визначення числа їхніх дійсних коренів, шукалися границі, між якими ці корені
можуть знаходитися. Нарешті, багато досліджень було присвячено методам
наближеного обчислення коренів: у технічних додатках звичайно досить знати лише
наближені значення коренів з деякою заздалегідь точністю і якби, наприклад,
корені многочлена записувалися в раидикалах, ці радикали все рівно були б
замінені їх наближеними значеннями.
Теоретична
частина
1.
Межі дійсних коренів
Щоб знайти корені
рівняння з достатнім степенем точності, треба знати, як ці корені розміщені на
комплексній площині або на дійсній осі. Заважимо, що іноді навіть немає
потреби знаходити числові значення коренів, а досить лише з‘ясувати їх
розміщення на площині (число дійсних, зокрема, додатних від‘ємних коренів
тощо). Наприклад, одна з важливих проблем механіки – теорія стійкості –
потребує з‘ясування умов, при яких усі корені даного алгебраїчного рівняння
мають від‘ємні дійсні частини.
Зробимо два
зауваження щодо комплексних коренів многочленів.
Зауваження 1. Усі корені многочлена 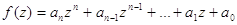 лежать у середині круга з
центром у точці 0 і радіусом лежать у середині круга з
центром у точці 0 і радіусом
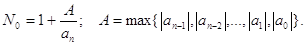 (1) (1)
Зауваження 2. Комплексні корені многочлена
з дійсними коефіцієнтами розміщені симетрично відносно дійсної осі.
Переходячи тепер
до розгляду дійсних коренів многочленів з дійсними коефіцієнтами, будемо знову
позначати змінне буквою x, а не z.
З наведеного
зауваження 1 дістаємо таке твердження:
Теорема. Усі дійсні корені рівняння 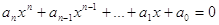 міститься в інтервалі міститься в інтервалі 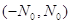 , де , де
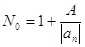 , , 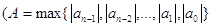 . .
Справді, всі
комплексні корені лежать у крузі 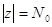 , а
тому, якщо серед них є дійсні корені, то вони повинні потрапити в зазначений
інтервал. , а
тому, якщо серед них є дійсні корені, то вони повинні потрапити в зазначений
інтервал.
Теорему 1 часто
називають теоремою про межі коренів рівняння. Є чимало способів, які дають
змогу з більшою точністю встановлювати межі дійних коренів алгебраїчних
рівнянь. Розглянемо один з них, так званий спосіб Ньютона.
Зробимо деякі
зауваження.
Число 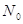 , визначене за теоремою 1,
дає одночасно верхню межу додатних коренів многочлена і нижню межу його від’ємних
коренів, бо вказує інтервал , визначене за теоремою 1,
дає одночасно верхню межу додатних коренів многочлена і нижню межу його від’ємних
коренів, бо вказує інтервал 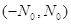 , в
якому лежать усі дійсні корені, якщо вони існують. Один з шляхів уточнення,
звуження меж, між якими слід шукати дійсні корені, полягає в тому, щоб окремо
знаходити нижню і верхню межі додатних коренів та нижню і верхню межі від’ємних
коренів даного многочлена, тобто такі чотири числа , в
якому лежать усі дійсні корені, якщо вони існують. Один з шляхів уточнення,
звуження меж, між якими слід шукати дійсні корені, полягає в тому, щоб окремо
знаходити нижню і верхню межі додатних коренів та нижню і верхню межі від’ємних
коренів даного многочлена, тобто такі чотири числа 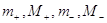 ,
що всі додатні корені многочлена лежать в інтервалі ,
що всі додатні корені многочлена лежать в інтервалі  ,
а всі від’ємні – ,
а всі від’ємні – 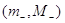 . Якщо многочлена
моє корінь нуль, досить розглянути многочлена, утворений з даного ділення на x. . Якщо многочлена
моє корінь нуль, досить розглянути многочлена, утворений з даного ділення на x.
Завдання
полегшується тим, що фактично досить знати спосіб знаходження лише одного з цих
чотирьох чисел, наприклад 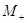 –
верхньої межі додатних коренів. Знаходження інших трьох меж дійсних коренів
рівняння –
верхньої межі додатних коренів. Знаходження інших трьох меж дійсних коренів
рівняння 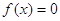 легко звести до
знаходження верхньої межі додатних коренів деяких допоміжних рівнянь. легко звести до
знаходження верхньої межі додатних коренів деяких допоміжних рівнянь.
Так, зробивши в
рівнянні 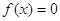 заміну змінного заміну змінного 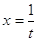 , дістанемо рівняння , дістанемо рівняння 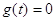 , корені якого , корені якого 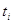 зв’язані з відповідними
коренями зв’язані з відповідними
коренями 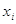 заданого рівняння
співвідношенням заданого рівняння
співвідношенням 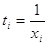 . Якщо . Якщо 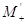 – верхняя межа додатних
коренів рівняння – верхняя межа додатних
коренів рівняння 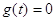 , тобто , тобто 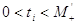 , то , то 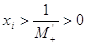 , звідки видно, щ за нижню
додатних коренів рівняння , звідки видно, щ за нижню
додатних коренів рівняння 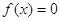 можна
взяти число можна
взяти число 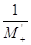 : : 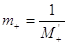 . .
Аналогічно,
заміна 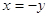 переводить рівняння переводить рівняння 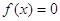 в рівняння в рівняння 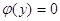 , корені якого , корені якого 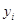 зв’язані з відповідними
коренями зв’язані з відповідними
коренями 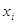 рівняння рівняння 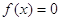 рівністю рівністю 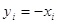 . Якщо . Якщо 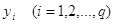 – всі додатні корені
рівняння – всі додатні корені
рівняння 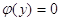 , то , то 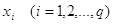 – всі від’ємні корені
рівняння – всі від’ємні корені
рівняння 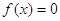 . З нерівності . З нерівності 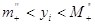 видно, що видно, що 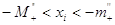 , тобто верхня і нижня межі
від’ємних коренів рівняння , тобто верхня і нижня межі
від’ємних коренів рівняння 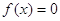 виражаються
через межі додатних коренів рівняння виражаються
через межі додатних коренів рівняння 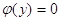 : : 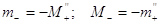 . .
Отже досить мати
правило для знаходження верхньої межі додатних коренів многочлена.
2.
Число дійсних коренів
Знання числа і
розміщення дійсних коренів многочленів є важливою передумовою застосування
багатьох методів чисельного розв’язування рівнянь. В окремих випадках деякі
відомості про число дійсних коренів можна дістати за допомогою досить
поверхневого аналізу. Іноді при знаходженні меж коренів виявляється, що
многочлена не має додатних або від’ємних коренів. Однак для повної відповіді
на питання про число дійсних коренів многочлена з дійсними коефіцієнтами (або
навіть про число таких коренів на довільному, наперед заданому інтервалі
дійсної осі) потрібні більш глибокі дослідження.
У багатьох
випадках число дійсних коренів рівняння з дійсними коефіцієнтами можна
визначити за простим правилом, яке дав Декарт. Перш ніж формулювати це правило,
зробимо деякі зауваження.
Зауваження 1. Розглядатимемо кількість змін
знаків у даній упорядкованій скінченій послідовності дійсних чисел 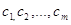 розуміючи під цим
кількість пар сусідніх чисел цієї послідовності, які мають протилежні знаки. Наприклад,
у послідовності –1,-2,6,3,-1,4 є 3 зміни знаків, а в послідовності
–1,-2,-6,-3,-1,-4 є 0 змін знаків. Якщо які-небудь з чисел розуміючи під цим
кількість пар сусідніх чисел цієї послідовності, які мають протилежні знаки. Наприклад,
у послідовності –1,-2,6,3,-1,4 є 3 зміни знаків, а в послідовності
–1,-2,-6,-3,-1,-4 є 0 змін знаків. Якщо які-небудь з чисел 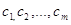 дорівнюють нулю, то при
підрахунку числа змін знаків їх до уваги не беруть. Зауважимо, що коли перше й
останнє числа дорівнюють нулю, то при
підрахунку числа змін знаків їх до уваги не беруть. Зауважимо, що коли перше й
останнє числа 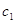 і і 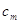 даної послідовності мають
однакові знаки, то кількість змін знаків у послідовності парна; якщо ж даної послідовності мають
однакові знаки, то кількість змін знаків у послідовності парна; якщо ж 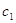 і і 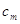 мають протилежні знаки, то
кількість змін знаків – непарна. Справді, члени послідовності, які
безпосередньо йдуть за кожною зміною знаків, мають знак, протилежний знаку тих
членів, які передували зміні знаків. Отже, якщо остання зміна знаків має
непарний номер, то числа послідовності, що йдуть за нею (і зокрема, мають протилежні знаки, то
кількість змін знаків – непарна. Справді, члени послідовності, які
безпосередньо йдуть за кожною зміною знаків, мають знак, протилежний знаку тих
членів, які передували зміні знаків. Отже, якщо остання зміна знаків має
непарний номер, то числа послідовності, що йдуть за нею (і зокрема, 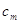 ) матимуть знак,
протилежний до ) матимуть знак,
протилежний до 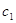 . .
Зауваження 2. Припускатимемо, що
розглядуваний многочлена не має кратних коренів, оскільки завжди можна
відокремити кратні множники.
Правило
Декарта. Число
додатних коренів многочлена з дійсними коефіцієнтами
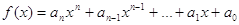
дорівнює числу
змін знаків у послідовності його коефіцієнтів або на парне число менше.
Зауваження 1. Правило Декарта можна
застосувати і для оцінки числа від’ємних коренів з дійсними коефіцієнтами. Для
цього в рівнянні
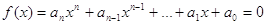
треба зробити
заміну змінного 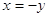 . Зрозуміло, що
число від’ємних коренів даного рівняння дорівнює числу додатних коренів
рівняння . Зрозуміло, що
число від’ємних коренів даного рівняння дорівнює числу додатних коренів
рівняння 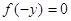 , яке можна оцінити за
правилом Декарта. , яке можна оцінити за
правилом Декарта.
Якщо дане
рівняння повне, тобто жодний коефіцієнт не дорівнює нулю, то число від’ємних
коренів можна визначити і не виконуючи заміни 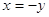 .
Справді, в цьому випадку число .
Справді, в цьому випадку число 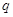 змін
збережень знаків у ряді коефіцієнтів многочлена змін
збережень знаків у ряді коефіцієнтів многочлена 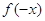 дорівнює
числу дорівнює
числу  збережень знаків у ряді
коефіцієнтів многочлена збережень знаків у ряді
коефіцієнтів многочлена 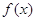 . Отже,
число . Отже,
число 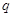 від’ємних коренів повного
рівняння дорівнює числу від’ємних коренів повного
рівняння дорівнює числу 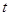 збережень знаків
у ряді його коефіцієнтів або на парне число менше. збережень знаків
у ряді його коефіцієнтів або на парне число менше.
Зауваження 2. Коли наперед відомо, що всі
корені даного рівняння 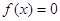 дійсні,
то правило Декарта дає точну відповідь на питання про число дійсних коренів, а
саме: число додатних коренів дорівнює числу змін знаків у ряді коефіцієнтів
многочлена дійсні,
то правило Декарта дає точну відповідь на питання про число дійсних коренів, а
саме: число додатних коренів дорівнює числу змін знаків у ряді коефіцієнтів
многочлена 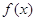 , а число від’ємних коренів
– числу змін знаків у ряді коефіцієнтів многочлена , а число від’ємних коренів
– числу змін знаків у ряді коефіцієнтів многочлена 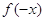 . .
Справді, нехай,
як і вище, 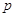 і і 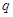 – число додатних і
від’ємних коренів даного многочлена – число додатних і
від’ємних коренів даного многочлена 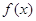 , ,  -го степеня; -го степеня; 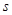 і і 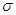 – число змін знаків у ряді
коефіцієнтів многочлена – число змін знаків у ряді
коефіцієнтів многочлена 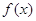 і
многочлена і
многочлена 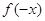 відповідно. З умови, що
всі корені дійсні, випливає: відповідно. З умови, що
всі корені дійсні, випливає: 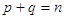 . Якби
рівняння були повними, то мали б також . Якби
рівняння були повними, то мали б також 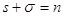 .
Якщо ж деякі з коефіцієнтів многочлена .
Якщо ж деякі з коефіцієнтів многочлена 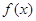 (а
тому й многочлена (а
тому й многочлена 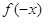 ) перетворюється
в нуль, то числа ) перетворюється
в нуль, то числа 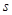 і і 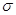 можуть тільки зменшитися.
Тому в загальному випадку можуть тільки зменшитися.
Тому в загальному випадку 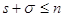 , звідки , звідки
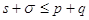 , або , або 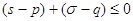 . Але з правила Декарта
знаємо, що . Але з правила Декарта
знаємо, що 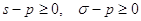 . Тому насправді . Тому насправді 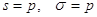 . .
На жаль, у
більшості випадків наперед невідомо, чи всі корені рівняння дійсні. У зв’язку з
цим правило Декарта, хоч і зручне з точки зору простоти застосування, не дає
повної відповіді на питання про число дійсних коренів рівнянь з дійсними
коефіцієнтами та їх розподіл між додатною і від’ємною півосями.
Практична
частина
1.
Опис програми
Програма
складається з двох файлів – polinom.pas і polinom.dat. У файлі polinom.dat
записується степень многочлена та його коефіціенти.
Описаняя процедур
та функцій:
procedure znach –
шукає межі додатніх та ві’ємних коренів;
function
znachenie – знаходить значення многочлена в точці;
procedure delenie
– відокремлює корені многочлена;
procedure korni –
уточнює корені многочлена методом поділу відрізка навпіл;
2.
Текст програми
Uses crt;
type
ff=array[0..10] of real;
var
f0,f1,f2,f3:ff;
prom,kpol:array[0..100] of real;
fil:text;
i,nf,k,iprom:integer;
n0,n1,n2,n3,b:real;
procedure
znach(a100:ff ;var a1:ff); {ищет промижутки}
var i1:byte;
begin
if
a100[0]<0 then
for i1:=0 to
nf-1 do a100[i1]:=-1*a100[i1];
k:=0;
for i1:=0 to
nf-1 do
if
a100[i1]<0 then begin k:=i1;break end;
b:=0;
for i1:=0 to
nf-1 do
if
a100[i1]<0 then if b<abs(a100[i1]) then b:=abs(a100[i1]);
a1:=a100;
end;
procedure
gran(k1:integer;b1,a5:real;var nk:real);{границы}
begin
if
(k1<>0)and(b1<>0) then nk:=1+exp(1/k1*ln(b1/a5))
else nk:=0;
end;
function
znachenie(a100:ff;xx:real):real; {значение в тч ХХ}
var y:real;
i100:integer;
begin
y:=a100[0];
for i100:=1 to
nf-1 do
y:=y*xx+a100[i100];
znachenie:=y;
end;
procedure
delenie(a,b:real);
const dx=0.1;
var z,z1,c:real;
begin
iprom:=0;
prom[0]:=a;
While b>a
do begin
z:=znachenie(f0,a);
c:=a;
repeat
a:=a+dx;
z1:=znachenie(f0,a);
until
(z*z1<0)or(b<a);
if z*z1<0
then begin iprom:=iprom+1;
prom[iprom-1]:=c;
prom[iprom]:=a;
end;
end;
end;
procedure
korni(a8,b8:real);
const eps=0.0001;
var x0:real;
begin
x0:=(a8+b8)/2;
while
abs(b8-a8)>eps do begin
if
znachenie(f0,a8)*znachenie(f0,X0)<0 then begin b8:=x0;end;
if
znachenie(f0,x0)*znachenie(f0,b8)<0 then begin a8:=x0;end;
x0:=(a8+b8)/2 end;
kpol[i]:=x0;
end;
begin clrscr;
assign(fil,
‘polinom.dat’);
reset(fil);
write(‘f=’);
readln(fil,nf);
{****************************************}
for i:=0 to
nf-1 do {begin }
read(fil,f0[i]);write(f0[i],’ ‘)end;
writeln;
znach(f0,f0);
gran(k,b,f0[0],n0);
{*****************************************}
for i:=0 to
nf-1 do f1[i]:=f0[nf-1-i];
znach(f1,f1);
gran(k,b,f1[0],n1);
{******************************************}
for i:=0 to
nf-1 do
if
odd(nf-1-i)=true then f2[i]:=-1*f0[i]
else
f2[i]:=f0[i];
znach(f2,f2);
gran(k,b,f2[0],n2);
{************************************************}
for i:=0 to
nf-1 do
if
odd(nf-1-i)=true then f3[i]:=-1*f0[nf-1-i]
else
f3[i]:=f0[nf-1-i];
znach(f3,f3);
gran(k,b,f3[0],n3);
if n0<>0
then begin
writeln(‘відрізок додатних коренів [‘,1/n1:1:3,’ ; ‘,n0:1:3,’]’);
delenie(1/n1,n0);
for
i:=0 to iprom-1 do begin
korni(prom[i],prom[i+1]);
writeln(kpol[i]:1:2{,’ ‘,znachenie(f0,kpol[i]):1:2}); end; end
else
writeln('немає додатніх коренів');
if
n3<>0 then begin
writeln('Відрізок від’ємних коренів [',-1*n2:1:3,' ; ',-1/n3:1:3,']');
delenie(-1*n2,-1/n3);
for
i:=0 to iprom-1 do begin
korni(prom[i],prom[i+1]);
writeln(kpol[i]:1:2,’ ‘,znachenie(f0,kpol[i]):1:2); end; end
else
writeln('немає від’ємних коренів');
readkey;
end.
3.
Контрольні приклади
x3-4x2-7x+10=0
відрізок додатних
коренів [0,588;8,000]
1,00
5,00
відрізок
від’ємних коренів [-4,162;-0,163]
-2,00
x5+2x4-5x3+8x2-7x-3=0
відрізок додатних
коренів [0,380;3,646]
1,31
відрізок
від’ємних коренів [-9,000;-0,273]
-3,91
-0,30
3x5+7x4-8x3+5x2-2x-1=0
відрізок додатних
коренів [0,274;2,633]
0,77
відрізок
від’ємних коренів [-3,667;-0,111]
-3,31
-0,26
x3-2,8x2-0,35x+3,45-0
відрізок додатних
коренів [0,552;3,800]
1,50
2,30
відрізок
від’ємних коренів [-9,000;-0,273]
-1,00
Висновок
В курсовій роботі
були розглянуті методи наближеного пошуку меж та самих коренів многочлена з
дійсними коренями. Можна знайти багато інших методів наближеного знаходження
коренів. Один з них найбільш вдосконалим є метод Лобачевського. Цей метод
дозволяє знаходити наближення значення всіх коренів відразу, у тому числі і
комплексних, причому не потребує відділення коренів; однако він зв’язан з
великими обчисленнями.
Література
1. А. Г. Курош «Курс высшей алгебры», «Наука», Москва
1975
2. С. Т. Завало, В. М. Костарчук, Б. И. Хацет «Алгебра
и теория чисел», Том 1,«Высшая школа», Киев 1974
3. С. Т. Завало, В. М. Костарчук, Б. И. Хацет «Алгебра
и теория чисел», Том 2,«Высшая школа», Киев 1976
|