Курсовая работа: MathML (Mathematical Markup Language)
Курсовая работа: MathML (Mathematical Markup Language)
Содержание
1. MathML (Mathematical Markup Language)
1.1 Математика и ее система обозначений
1.2 Истоки и цели
1.2.1 История MathML
1.2.2 Ограниченность HTML
1.2.3 Требования к математической разметке
1.2.4 Цели проекта MathML
1.3 Роль MathML в Сети
1.3.1 Существующие языки математической разметки
1.3.2 Механизм расширения HTML
1.3.3 Механизм расширения браузера
1.4 Обзор MathML
1.4.1 Таксономия элементов MathML
1.4.2 Разметка представления
1.4.3 Разметка содержания
1.4.4 Объединение представления и содержания
1.5 MathML в документах
1.6 Примеры MathML
1.6.1 Примеры разметки представления
1.6.2 Примеры разметки содержания
1.6.3 Примеры смешанной разметки
1.7 Синтаксис и грамматика MathML
1.7.1 Синтаксис и грамматика MathML
1.7.2 Пример синтаксиса XML
1.7.3 Дочерние элементы против аргументов
1.7.4 Значения атрибутов MathML
1.7.4.1 Синтаксические нотации, используемые в спецификации
MathML
1.7.4.2 Атрибуты с единицами измерения
1.7.4.3 CSS-совместимые атрибуты
1.7.4.4 Значения атрибутов по умолчанию
1.7.4.5 Значения атрибутов в MathML DTD
1.7.5 Атрибуты, общие для всех элементов MathML
1.7.6 Свертывание пробелов во вводе
2. Возможности современных браузеров
при работе с MathML
2.1 Mozilla & Firefox
2.2 Microsoft Internet Explorer
2.3 Opera
Список использованной литературы
MathML (Mathematical Markup Language) представляет собой язык
разметки математических приложений, основанный на XML. Он был разработан
Консорциумом WWW (W3C) и принят в качестве Рекомендации. Текущей версией
является Mathematical Markup Language (MathML) Version 2.0 (Second Edition),
утвержденной 21 октября 2003 года.
MathML реализует две "точки зрения" на
математическую разметку. Один из ее видов - это разметка представления (Presentation
Markup), которая описывает визуальную форму представления математической
формулы. Второй - разметка содержания (Content Markup), выражающая
семантическое содержание.
MathML рассматривает не только представление, но и смысл
элементов формулы. Также разрабатывается система разметки математической
семантики, призванная дополнить MathML. Она называется OpenMath.
Характерной чертой математической информации является
использование сложной и высокоразвитой двумерной символьной системы обозначений.
Однако, как писал J. R. Pierce в своей книге по теории коммуникации, математика
и ее нотация не должны рассматриваться как одно и то же. Математические идеи
существуют независимо от способа их представления. Тем не менее, взаимосвязь
между значением и обозначением весьма тонка, и в возможности представлять и
манипулировать идеями в символьной форме кроется значительная мощь
математического аппарата, как инструмента описания и анализа. Основная
трудность при внедрении математики в World Wide Web состоит в том, чтобы зафиксировать
как представление, так и содержание (то есть значение) таким образом, чтобы в
документах максимально использовать высокоразвитую систему математической
нотации и потенциал взаимодействия в электронных средствах информации.
Математическая система обозначений постоянно развивается,
так как люди постоянно совершенствуют способы представления идей. Даже
стандартная система обозначения арифметических действий прошла через
удивительное многообразие стилей, включая множество ныне несуществующих,
поддерживающих математические обозначения своего времени. Современная
математическая система обозначений является продуктом вековых
усовершенствований, и принятые обозначения для высококачественной печати
достаточно сложны. Например, переменные и буквы, обозначающие числа, сейчас
обычно печатаются специальным математическим курсивом чуть отличным от обычного
текстового курсива. Пробелы, окружающие символы операций такие как +, - ,×
и /, немного отличаются от таковых в тексте, отражая соглашения о старшинстве
оператора. Целые книги посвящены правилам набора математических текстов, от
выравнивания верхних и нижних индексов до правил для выбора размеров круглых
скобок и специальных нотационных соглашений для различных областей математики.
Принятая система обозначений в математике, и в печатном
тексте вообще, направлена на то, чтобы зрительно выделить и сделать напечатанные
выражения более легкими для чтения и понимания. Хотя это и кажется очевидным,
но мы полагаемся на сотни соглашений таких как параграфы, заглавные буквы,
семейства шрифтов, и даже механизм десятичной нумерации разделов, подобный
тому, что мы используем в этом документе (заслуга G. Peano, который вероятно
более известен своими аксиомами для натуральных чисел). Таким образом,
нотационные соглашения, наверное, даже более важны для электронных медиа, где
требуется бороться с трудностями чтения с экрана.
Однако, внедрение математики в Сеть это не просто поиск
способов отображения математической информации в окне браузера. Сеть
представляет фундаментально новый подход к хранению знаний, в котором
взаимосвязь играет центральную роль. Становится все более и более важно найти
способы взаимосвязи математических документов, которые облегчат автоматическую
обработку, индексацию и повторное использование в других математических
приложениях и контекстах. Подобные усовершенствования в технологии коммуникации
позволяют расширить наши возможности в представлении и кодировании
математического материала. Мы надеемся, что MathML является важным шагом в этом
направлении.
Задача представления математической информации для
компьютерной обработки и электронных средств коммуникации возникла задолго до
появления Интернета. Раньше общей практикой для ученых была запись статей в
неком виде, основанном на ASCII-символах и дальнейшая пересылка их друг другу
по электронной почте. Несколько языков математической разметки, в частности TEX,
уже широко использовались в 1992 году, еще до того, как Сеть заняла столь
значимое положение.
С самого начала Сеть зарекомендовала себя, как весьма
эффективный способ сделать информацию доступной большому количеству людей. Однако,
даже при том, что World Wide Web была изначально задумана и реализована учеными
для ученых, возможности для включения математических выражений в HTML были
крайне ограничены. В настоящее время, большая часть математической информации в
Сети представлена в виде текста с графическими изображениями научных выражений
(в формате GIF или JPEG) или в виде
целых документов в формате PDF.
Консорциум World Wide Web (W3C) понимал, что отсутствие
основ для научной коммуникации является серьезной проблемой. Уже в 1994 году
Dave Raggett внес предложение о включении HTML Math в прототип HTML 3.0. На
конференции в Дармштадте в апреле 1995 года был проведен круглый стол по
математической разметке. В ноябре того же года представители Wolfram Research
выдвинули предложение команде W3C о реализации поддержки математики в рамках
HTML. Важную роль в объединении многих заинтересованных сторон сыграла
проведенная в мае 1996 года встреча Digital Library Initiative в
Champaign-Urbana. Результатом этой встречи стало формирование редакционного
наблюдательного совета по HTML Math. Впоследствии эта рабочая группа
разрослась, и в марте 1997 года была формально повторно сформирована как первая
W3C Math Working Group. Вторая W3C Math Working Group была сформирована в июле
1998 года.
Проект MathML отражает интересы и мнения различных групп
специалистов. Многое в развитии MathML заслуживает специального упоминания. Например,
это касается вопроса общедоступности, где были особенно ощутимые затруднения. В
этом направлении много работы проделал T. V. Raman. Neil Soiffer и Bruce Smith
из Wolfram Research поделились своим опытом в решении проблем представления
математического материала, накопленным при работе над проектом Mathematica 3.0.
Их идеи оказали важное влияние на структуру элементов представления. Paul
Topping из Design Science также внес свой вклад в математическое форматирование
и редактирование. Много пользы извлек MathML из партнерства с рядом членов
рабочих групп, связанных с другими работами по кодированию математической
информации в SGML и в сообществах компьютерной алгебры. В
их числе Stephen Buswell из Stilo Technologies, Nico Poppelier из Elsevier Science Stéphane Dalmas из INRIA (Sophia Antipolis), Stan Devitt из Waterloo Maple, Angel Diaz и Robert S. Sutor из IBM, и Stephen M. Watt из University of Western Ontario.
Также, на MathML повлиял проект OpenMath, работа рабочей группы ISO 12083 и
работа Stilo Technologies над фрагментом DTD для 'семантической' математики. Американское
математическое общество играло ключевую роль в развитии MathML. Помимо прочего,
председателями обеих W3C Math Working Group стали представители этой
организации. С мая 1996 по март 1997 года группу вел Ron Whitney. Patrick Ion
был сопредседателем группы с марта 1997 по июнь 1998 вместе с Robert Miner из
The Geometry Center, а с июля 1998 вместе с Angel Diaz из IBM.
Спрос на эффективные средства обмена научной информацией
остается по-прежнему высоким. Все больше и больше исследователей, ученых,
инженеров, учителей, студентов, работая в различных местах земного шара,
полагаются на электронные средства коммуникации. В тоже время, методы
распространения научной нотации, основанные на графическом представлении,
преобладающие сейчас в Сети, примитивны и неадекватны. Качество документов
оставляет желать лучшего, создание - сложно, а математическая информация,
содержащаяся в картинках, не доступна для поиска, индексации и повторного
использования в других приложениях.
Существует две основных проблемы с использованием HTML.
Проблема отображения. Рассмотрим уравнение 22x=10. Размеры
изображения подобраны так, чтобы соответствовать окружающему тексту размера 14 pt
в системе, где оно было создано. Естественно, что в других системах или при
другом размере текста уравнение будет выглядеть не так, как задумывал автор. Кроме
того, изображение с этим уравнением создавалось в предположении, что у
документа будет белый фон. Таким образом, если читатель или браузер установит
другой цвет страницы, то в результате вокруг текста возникнет белый "ореол".
Далее рассмотрим уравнение
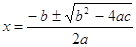 , ,
которое служит примером выравнивания горизонтальной оси
изображения по верху строчных букв в окружающем тексте. В этом уравнении
присутствует знаменатель, и базисная линия располагается на расстоянии около
одной трети от низа изображения. Это уравнение, например, можно разместить так:
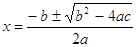 , ,
то есть так, чтобы горизонтальная ось изображения и базисная
линия уравнения совпадали, но это приведет к проблемам с межстрочными
интервалами. В результате этого текст станет тяжело читаемым. Кроме того,
вертикальное выравнивание по центру отличается в различных браузерах, делая
невозможным гарантировать правильное расположение формул для различных
пользователей.
Уравнения, оформленные в виде изображений, обычно труднее
воспринимать, чем окружающий текст. Более того, эти проблемы только
увеличиваются, если документ напечатать. Разрешение изображений около 70 точек
на дюйм, тогда как окружающий текст обычно имеет 300, 600 или более точек. Такая
разница в качестве неприемлема для большинства людей.
Проблемы кодирования. Попытаемся найти в этом документе
фрагмент, например, '=10' первого уравнения выше. Или попробуем скопировать и
вставить уравнение в другое приложение; более того, попробуем скопировать и
вставить только фрагмент уравнения. При использовании методов, основанных на
графическом представлении, ни одна из этих задач не может быть решена. И хотя
использование атрибута alt в документе может немного помочь, ясно, что
интерактивные web - документы должны предоставлять
более продвинутый интерфейс между браузерами и математической информацией.
Другая проблема использования изображений для математических
объектов - необходимость высокой пропускной способности канала связи. Представление
уравнения разметкой обычно меньше по объему и лучше сжимаемо по сравнению с
представлением в виде изображения. Кроме того, при использовании разметки для
записи уравнений большая часть работы по отображению перекладывается на
клиентскую машину.
Некоторые проблемы, связанные с включением математических
выражений в HTML-документ в виде изображений, могут быть решены с помощью
улучшения обработки последних браузерами. Хотя, даже если такое и произойдет,
останется проблема доступа к информации, содержащейся в математических
выражениях из других приложений. Поэтому, в будущем, улучшение методов,
основанных на графическом представлении неперспективно. Для полной интеграции
математического материала в web-документ необходимо представление математической
нотации с помощью языка разметки.
При создании любого языка разметки необходимо тщательно
учесть потребности его потенциальных пользователей. В случае с MathML область
применения простирается от сферы образования до сферы исследований и даже
бизнеса.
Сфера образования является большой и важной областью, в
которой должна быть обеспечена возможность размещения в Сети научных материалов
для занятий. В тоже время, преподаватели ограничены во времени и оборудовании,
и обычно останавливаются перед сложностью создания технических web-документов. Студенты и преподаватели должны иметь
возможность быстро и легко создавать математические документы, используя
интуитивно понятные, легкие для изучения и "дешевые" инструменты.
Электронные учебники - другой способ использования Сети,
который потенциально очень важен для образования. Известный специалист по
управлению Peter Drucker прогнозировал конец эпохи построения системы высшего
образования вокруг больших университетских городков и начало ее распространения
через Сеть. Электронные учебники должны быть более интерактивными и позволять
связывать текст с научным программным обеспечением.
Академические и коммерческие исследовательские группы
постоянно выпускают большое количество научного материала. Все больше и больше
научных публикаций размещается в базах данных, таких как довольно известный
архив препринтов по физике и математике Национальной Лаборатории в Лос-Аламосе
(Los Alamos). В особенности это относится к некоторым областям физики и
математики, где цены на академические журналы весьма высоки. К тому же, базы
данных с информацией о математических исследованиях, такие как Mathematical
Reviews и Zentralblatt für Mathematik, предлагают огромное количество
ссылок на содержащиеся в Сети математические документы.
Для соответствия требованиям исследовательского сообщества,
язык математической разметки должен упростить обслуживание и работу с большими
объемами документов, где крайне важны автоматический поиск и индексация. Из-за
большого количества уже существующих математических документов, особенно в
формате TEX, также немаловажно иметь возможность конвертации между
существующими форматами и любым новым. И наконец, для научных исследований
жизненно необходима возможность хранить информацию в архивах.
Многие ученые и инженеры используют в своей работе
технические документы для обмена и записи результатов экспериментов, а также
для компьютерного моделирования и проверки проведенных вычислений. Для такого
рода использования методы размещения математической информации в Сети должны
предоставлять стандартный способ совместного ее использования так, чтобы можно
было легко ее прочитать, обработать и создавать с использованием доступных и
простых инструментов.
Другое общее требование заключается в возможности
отображения математического материала в других информационных средах, таких как
речь или шрифт Брайля, которые крайне важны для людей с нарушением зрения.
Коммерческие издательства также заинтересованы в продвижении
методов представления математической информации в Сети в различном виде от
электронных версий обычных книг до интерактивных учебников и академических
журналов. Издательствам требуется такой способ размещения математических
документов в Сети, который бы имел возможность для высококачественного вывода,
был применим для крупномасштабного коммерческого использования и, по
возможности, совместим со старыми системами, в частности, на основе SGML.
Для соответствия различным требованиям научного сообщества
MathML разрабатывался с учетом следующих условий.
MathML должен:
Представлять математический материал так, чтобы он подходил
для обучения и научной коммуникации любого типа.
Представлять как математическую нотацию, так и
математическое содержание.
Обеспечивать возможность преобразования между ним и другими
математическим форматами, как презентационными, так и семантическими. Форматы
вывода должны включать:
графическое отображение
синтезаторы речи
форматы систем компьютерной алгебры
форматы других языков, таких как TEX
отображение в виде простого текста, например, эмуляторы
VT100
печатные устройства, включая работающие со шрифтом Брайля
Понятно, что такие преобразования могут привести к некоторой
потере информации.
Иметь возможность включения информации, необходимой для
определенных средств отображения и других приложений.
Поддерживать корректный просмотр длинных выражений.
Обеспечивать расширяемость.
Поддерживать шаблоны и другие средства редактирования
математической информации.
Быть понятным человеку и простым для программной обработки.
В независимости от того, насколько удачен MathML как язык
разметки, он будет полезен только в случае грамотного его применения. W3C Math
Working Group определила короткий список дополнительных целей его реализации. В
нем кратко описана минимальная функциональность, которую должны обеспечивать
программы отображения и обработки MathML.
Выражения MathML внутри страниц HTML (и XHTML) должны
корректно отображаться в наиболее распространенных браузерах в соответствии с
установками читателя и автора, при этом должно обеспечиваться качество,
максимально достижимое на данной платформе.
Документы HTML (и XHTML), содержащие выражения MathML,
должны корректно выводиться на печать с высоким разрешением.
Выражения MathML, включенные в web-страницы, должны
реагировать на действия пользователя, такие как работа с мышью, и осуществлять
взаимодействие с другими приложениями через браузер.
Редакторы и конвертеры математических выражений должны
разрабатываться с учетом возможности создавать web-страницы, содержащих
выражения MathML.
В ближайшее время для решения проблемы отображения
планируется использовать встраиваемые элементы, такие как Java-апплеты, плагины
и элементы управления ActiveX. Однако объем, в котором будет это реализовано,
зависит от сотрудничества и поддержки производителей браузеров и другого
програмного обеспечения. W3C Math Working Group продолжает работу с рабочими
группами по Document Object Model (DOM) и Extensible Style Language (XSL),
чтобы гарантировать, что нужды научного сообщества будут удовлетворены в
будущем. Ясно, что MathML 2.0 является значительным шагом вперед по сравнению с
MathML 1.0 Recommendation (Апрель 1998).
Цели разработки MathML требуют гибкой и расширяемой системы
записи математического материала, позволяющей взаимодействовать с внешними
программами и осуществлять высококачественное отображение в различных
информационных средах. Но любой язык разметки, удовлетворяющий всем этим
требованиям, достаточно сложен.
В то же время, для многих групп пользователей, например,
студентов, важно иметь простой путь для включения математических выражений в web-страницы. Аналогично, для других групп, например, для
пользователей системы TEX, лучшим решением была бы система,
позволяющая непосредственное включение в web-страницы
разметки при помощи языка, подобного TEX. В общем, различным группам
пользователей требуются различные формы ввода и вывода информации, наиболее соответствующие
их потребностям. Следовательно, в идеале система для размещения математических
документов в Сети должна предоставлять как специализированные сервисы для ввода
и вывода, так и общие сервисы для обмена информацией и отображения в различных
информационных средах.
На практике, обзор того, что должен обеспечивать
математический стандарт в сети для специализированных и общих нужд, приводит к
идее многоуровневой архитектуры. Первый уровень включает стандартные мощные
средства обмена, обработки и отображения математических данных. Второй уровень
включает специализированные инструменты, предназначенные для конкретных групп
пользователей, с помощью которых можно легко кодировать математическую
информацию для ее распространения среди ограниченного круга пользователей.
MathML создан для разметки математической информации на
нижнем более общем уровнем двухуровневой архитектуры. Это предполагает разметку
сложной нотационной и семантической структуры в строгой, регулярной форме,
простой для обработки средствами отображения, поиска и индексации, а также
другими математическими приложениями.
Вследствие этого, разметка MathML не предполагает
непосредственного использования авторами. MathML понятен для человека, что
сильно помогает при отладке, но во всех случаях, за исключением простейших, он
слишком сложен для ручного кодирования. Вместо этого авторы должны будут
использовать специальные редакторы формул, конвертеры и другие
специализированные программные средства для создания документов MathML. В
качестве альтернативы, некоторые программы отображения и системы поддержки
математических документов могут преобразовывать другие входные форматы в MathML
"на лету".
В некотором смысле MathML аналогичен другим низкоуровневым
коммуникативным форматам, таким как язык PostScript, разработанный Adobe. Вы
можете создавать PostScript-файлы различными способами, в зависимости от ваших
потребностей: эксперты создают и правят их вручную, авторы создают их с помощью
текстовых процессоров, дизайнеры - программами-иллюстраторами и так далее. Если
у вас есть PostScript-файл, вы можете распространить его среди очень большой
аудитории, так как устройства отображения PostScript, такие как принтеры и
программы для просмотра на экране, широко доступны.
Одной из причин разработки MathML как языка разметки общего
коммуникативного уровня является стимулирование разработки математического
программного обеспечения Сети верхнего уровня. MathML представляет способ
координирования усилий разработчиков модулей программ для создания и
отображения математического материала. Упрощая разработку функциональных частей
большой системы, MathML может стимулировать разработку программ, которые будут
очень полезны потенциальным пользователям.
Авторы могут создавать MathML-документы, используя
инструменты, лучше подходящие для их нужд. Студенты могут предпочитать
визуальные редакторы формул, с возможностью сохранять блоки разметки MathML в
XHTML-файле. Исследователи могут использовать пакеты компьютерной алгебры,
автоматически кодирующие математическую информацию так, чтобы коллеги могли ее
взять из web-страницы и обработать. Издатели
академических журналов могут использовать программу, которая конвертирует
разметку TEX в HTML и MathML. Независимо от метода создания web-страницы,
содержащей MathML, становятся доступны все преимущества общего коммуникативного
слоя. Различные программы, работающие с MathML, могут быть использованы для
одного и того же документа, чтобы вывести его в систему воспроизведения речи и
на печать, а также для ввода в систему компьютерной алгебры и для управления им
как частью большого архива web-документов. Для высококачественной печати
математических документов в формате MathML часто проводится обратная
конвертация в стандартные системы верстки, включая TEX, который
специально создан для этих целей. Наконец, можно ожидать, что в конечном счете
MathML будет интегрирован в другие области, где встречаются математические
формулы, такие как электронные таблицы, пакеты статистической обработки данных
и средства инженерной разработки.
W3C Math Working Group сотрудничает с различными софтверными
компаниями для гарантии того, что скоро появятся различные программы для работы
с MathML, включая как средства создания документов, так и их отображения. Текущий
список программ, работающих с MathML расположен на странице Math World Wide Web
Consortium.
Первоначальная концепция HTML Math состояла
в том, чтобы просто расширить набор тэгов HTML и таким образом обеспечить
непосредственную интерпретацию в браузере. Однако еще до этого лавинообразный
рост сети сделал понятным, что требуется глобальный механизм расширений, а математическая
информация является только одним из типов структурированных данных, которые
могут быть интегрированы в Сеть с помощью такого механизма.
При условии, что MathML должен интегрироваться в Сеть в
качестве расширения, очень важно, чтобы MathML и использующие его программы
могли хорошо взаимодействовать с существующей web-средой.
В частности, MathML должен разрабатываться с учетом трех типов взаимодействия. Во-первых,
для создания математического контента важно, чтобы существующие языки
математической разметки могли быть преобразованы в MathML, и чтобы в
существующие редакторы была добавлена возможность создания документов MathML. Во-вторых,
должно обеспечиваться возможность вставлять разметку MathML в разметку HTML,
как ее дополнение, в этом случае, в будущем, она будет доступна для браузеров,
поисковых систем и всех типов web-приложений, которые
сейчас работают с HTML. И, наконец, должна обеспечиваться возможность
отображения MathML, встроенного в HTML, современными браузерами, даже если
результат будет далек от идеала. С переходом от HTML к XHTML все
вышеперечисленные требования станут еще более необходимыми.
World Wide Web полностью интернационален. Математика - язык,
использующийся во всем мире. Математическая нотация в науке и технике тесно
связана с национальными языками. W3C стремится быть конструктивной силой в
распространении коммуникативных возможностей в мире. Поэтому разработчики MathML
столкнулись с проблемой интернационализации. Неизвестно о несовместимости этой
версии MathML с языками с написанием слева направо. Запись слева направо
является стандартной в MathML 2, и понятно, что потребность в записи
математических формул в текстах на некоторых национальных языках еще не
возникала. Так называемая "двунаправленная технология" только
разрабатывается, и лучшая поддержка формул в этом контексте - задача будущих
разработок.
Возможно, наиболее значимое влияние на языки математической
разметки последних двух десятилетий оказала система верстки TEX,
разработанная Дональдом Кнутом (Donald Knuth). TEX является
стандартом de facto в математическом сообществе, и вообще широко распространен
среди ученых. TEX устанавливает стандарт качества для визуализации
документов, и много усилий было приложено, чтобы MathML мог обеспечить такое же
качество. Более того, так как существует множество документов в формате TEX,
и много людей, работающих с ней, основной при создании MathML была возможность
конвертации документов из формата TEX в формат MathML. Возможность
такой конвертации была продемонстрирована экспериментальными программами.
Обширная работа по кодированию математического материала
была также выполнена в сообществе SGML, и основанные на SGML схемы кодирования
широко используются коммерческими издателями. ISO 12083 - важный язык разметки,
содержащий фрагмент DTD первоначально предназначенный для описания визуального
представления математической нотации. Так как математическая нотация ISO 12083
и ее производные имеют много общего с TEX, и так как SGML более
регулярен и структурирован, чем TEX, многое из того, что сделано для
совместимости MathML с TEX, также хорошо применимо к ISO 12083.
MathML также уделяет большое внимание совместимости с
другими математическими программами и, в частности, с системами компьютерной
алгебры. Много элементов представления MathML частично основаны на механизме
печатных боксов (typesetting boxes). Элементы содержания MathML во многом
заимствованы из проекта OpenMath и работы Stilo Technologies по созданию
математического DTD. Проект OpenMath был тесно связан с сообществами SGML и
компьютерной алгебры. В этом проекте были предложены SGML и XML-основанные
способы взаимодействия между пакетами математических программ. Возможность
создания и интерпретации MathML в системах компьютерной алгебры была
продемонстрирована экспериментальными программами.
Как отмечено выше, успех HTML привел к попыткам интеграции в
Сеть различных типов данных и приложений. Каждый новый формат или приложение
потенциально накладывал новые требования на HTML и производителей браузеров. Через
некоторое время стало понятно, что необходим общий механизм для интеграции
новых расширений в HTML. Изначально, рабочая группа начала работу с идеей о
простом расширении HTML в духе первых попыток реализации поддержки математики в
HTML 3.2 Но при ближайшем рассмотрении, это оказалось не такой уж и хорошей
идеей. К моменту начала работ над MathML, XML стал доминирующим механизмом
общих расширений.
XML расшифровывается как eXtensible Markup Language. Он создан как упрощенная
версия SGML, метаязыка, используемого для определения грамматики и синтаксиса
HTML. Одна из целей XML - возможность применения в Сети, и в данном случае он
может быть рассмотрен как общий механизм расширений HTML. Как следует из его
названия, расширяемость - основная черта XML. Авторы получили возможность
объявлять и использовать новые элементы и атрибуты. В то же время, правила
грамматики и синтаксиса XML требуют обеспечения регулярной структуры документа
для реализации автоматической обработки и сопровождения больших объемов
документов. Строго говоря, XML является удобным способом описания древовидных
структур и, таким образом, может использоваться в качестве языка разметки.
К моменту образования первой W3C Math Working Group XML уже
имел широкую поддержку среди фирм-разработчиков, включая основных производителей
браузеров. Глобальный переход от HTML к XML важен для W3C. Промежуточным
результатом работы в этом направлении стало появление рекомендации XHTML,
которая определяет новую модульную форму HTML. MathML может рассматриваться как
один из модулей, который очень хорошо соответствует новому формату XHTML.
Кроме того, другие XML-приложения для всех видов публикации
и обработки документов обещают стать все более и более распространенными. Следовательно,
как с теоретической так и с практической точки зрения, было бы логично
определить MathML как XML-приложение.
К настоящему времени детали общей модели для отображения и
обработки XML-расширений в HTML в основном ясны, в отличие от ситуации, когда
была принята MathML 1.0 Recommendation. Предполагается, что свойства
форматирования (Formatting Properties), разработанные Cascading Style Sheets и
Formatting Properties Working Group для CSS и доступные через Document Object
Model (DOM), будут применяться для элементов MathML, чтобы получить
стилистический контроль над представлением MathML. Дальнейшая разработка
свойств форматирования проводится внутри рабочих групп CSS&FP и XSL.
На данный момент механизмы таблиц стилей не способны
обеспечить непосредственное отображение MathML браузером, поэтому необходимо
расширить возможности браузеров, используя встроенные объекты (embedded
elements) для отображения MathML. Уже возможно использовать в браузере
встроенный ограниченный механизм отображения для обработки встроенной
XML-разметки, такой как MathML, и обеспечивать взаимодействие ее с окружающей web-страницей,
однако, результаты пока не полностью соответствуют пожеланиям.
Для специализированной обработки, такой как связь с
системами компьютерной алгебры, возможность внешнего вызова других программ
останется особенно необходимой. Для того чтобы сложное взаимодействие между
браузерами и встроенными объектами было удовлетворительным, необходимо
определить достаточно богатую объектную модель документа. По этой причине W3C Math Working Group тесно сотрудничает с
Document Object Model (DOM) Working Group.
Для обработки встроенных элементов и для многосторонней
связи между научным программным обеспечением модель таблиц стилей в некоторых
случаях далека от идеала. Это может наложить дополнительные сложности
реализации в системе, когда можно получить некоторые преимущества, и это
накладывает требования к реализации взаимодействия между браузерами и
встроенными механизмами отображения, что, вероятно, будет недоступно в
ближайшем будущем.
По этим причинам спецификация MathML определяет
атрибут-ориентированную модель, которая показала себя в нескольких независимых
приложениях, как очень эффективная для высококачественного отображения сложных
математических выражений. Атрибуты представления MathML, где это возможно,
используют свойства форматирования W3C. Также, элементы MathML допускают
атрибуты class, style и id
для обеспечения совместимости с традиционными таблицами стилей CSS. Однако, в
настоящее время, имеется немного реализаций, где технология CSS используется
при отображении MathML.
Использование механизма стилевых таблиц CSS уже упоминалось
выше. Механизмы XSL также недавно стали доступны для преобразования
XML-документов в формат отображения. Действительно, альтернативные варианты
этой рекомендации, включая определяющую HTML-версию, были получены из
XML-источника, используя средства языка трансформаций XSL. Поскольку разработки
в этом направлении доступны для MathML, ожидается, что их использование станет
доминирующим методом стилистического контроля представлением MathML, который
предлагается для использования в отображающих средах, поддерживающих эти
механизмы.
Главной проблемой создания математического языка разметки
для применения в Сети является необходимость задавать одновременно
представление математической нотации и содержание представляемых математических
идеи или объекта.
Отношение математической нотации и математической идеи - тонкая
вещь. Формально, математическая логика поднимает вопросы о соответствии между
системами символьной логики и явлениями, которые они моделируют. На интуитивном
уровне, каждый, кто использовал математическую нотацию, знает как важен
правильный выбор нотации; символическая структура нотации предлагает структуру
логическую. Например, нотация Лейбница для производных предлагает цепь правил
вычисления через символические дроби.
Математики и учителя очень хорошо интуитивно чувствуют это; часть
их работы как раз и состоит в выборе нотации, которая подчеркивает ключевые
аспекты проблемы и скрывает или уменьшает несущественные. В математике очень
часто пишут что-либо, хотя строгое значение этого является совсем другим,
потому что опыт показывает, что это значительно лучше передает идею на высоком
уровне, чем строгие детали.
В других случаях, математическая нотация используется для
записи полного, точного значения свойств математического объекта. Математическая
нотация может быть потрясающе строгой и при аккуратном использовании полностью
свободной от неоднозначности. Более того, это отсутствие неоднозначности делает
возможным описать математические объекты так, что они могут быть использованы в
компьютерных приложениях, таких как системы компьютерной алгебры и системы
воспроизведения речи. В ситуации, когда главным является взаимодействие между
приложениями, детали визуального представления играют минимальную роль.
MathML позволяет авторам записывать как нотацию,
представляющую математический объект, и саму математическую структуру объекта. Более
того, авторы могут смешивать оба типа записи для определения представления и
содержания математической идеи. Оставшаяся часть этого раздела дает основное
представление о том, как MathML может быть использован для каждой из этих целей.
Все элементы MathML делятся на три группы: элементы
представления, элементы содержания и интерфейсные элементы.
Элементы представления описывают визуально ориентированную
двухмерную структуру математической нотации. Типичным примером является элемент
mrow, который обычно применяется для обозначения
горизонтального ряда частей выражения, и элемент msup,
который отмечает верхний индекс. Как правило, каждый элемент представления
соответствует одному типу нотационной схемы, такой как ряд, верхний индекс, нижний
индекс и так далее. Любая формула состоит из частей, которые могут состоять из
простейших элементов таких как цифры, буквы или другие символы.
Хотя предыдущий абзац связан с аспектом отображения
математической нотации, и, следовательно, разметкой представления, те же самые
рассуждения о декомпозиции применимы к абстрактным математическим объектам, а
значит и разметке содержания. Например, в контексте разметки содержания верхний
индекс обычно обозначает операцию потенцирования, требующую двух операндов: 'основания'
и 'показателя'. Это ни коим образом не является совпадением, так как обычно
математическая нотация тесно связана с логической структурой рассматриваемых
математических объектов.
Рекурсивная природа математических объектов и нотации
отражена в разметке MathML. Большинство элементов представления и содержания
содержат в себе другие элементы MathML, отвечающие за части, из которых
рекурсивно построен исходный объект. Первоначальная схема обычно называется
родительской, а части - дочерними. В общем, выражения MathML можно представить
в виде деревьев, где каждый узел соответствует элементу MathML, ветвь под
'родительским' узлом соответствует 'дочерним' узлам, и листья дерева
соответствуют атомарным элементам нотации или содержания, таким как числа,
символы и т.д.
Большинство элементов-листьев в дереве выражения MathML или
канонические пустые элементы без тела, или токены. Канонические пустые элементы
отображают символы в MathML, например, это делает элемент содержания <plus/>.
Токены - единственные элементы MathML, которые могут содержать текстовые данные.
Текстовые данные в MathML содержат символы Unicode и специальные символьные
конструкции, сделанные с помощью элемента mglyph. Третьим
типом элементов-листьев в MathML являются комментарии,
используемые для хранения данных, формат которых отличен от формата MathML.
Наиболее важными токенами представления являются mi,
mn и mo, используемые для
представления идентификаторов, чисел и операторов соответственно. Обычно эти
элементы отображаются разными стилями: числа - прямым шрифтом, идентификаторы -
наклонным, вокруг операторов оставляется дополнительное свободное пространство.
В разметке содержания содержится только три токена, ci,
cn и csymbol, для
идентификаторов, чисел и новых введенных в документ символов соответственно. В
разметке содержания существуют различные элементы для часто используемых
функций и операторов. Элемент apply применяется для
пользовательского расширения стандартного набора.
В терминах разметки, большинство элементов MathML
определяются открывающим и закрывающим тегами, которые ограничивают содержание
элемента. В случае токенов содержимое является текстовыми данными, в
большинстве остальных случаев - разметкой дочерних элементов. Элементы третьей
категории, называемые каноническими пустыми элементами, не требуют никакого
содержания и определяются одиночным тегом вида <name/>.
Примером может служить элемент <plus/> в разметке
содержания.
Давайте возьмем для примера выражение (a + b) 2
и рассмотрим на практике описанные выше принципы. Одним из вариантов разметки
представления для этого выражения будет такой:
<mrow>
<msup>
<mfenced>
<mrow>
<mi>a</mi>
<mo>+</mo>
<mi>b</mi>
</mrow>
</mfenced>
<mn>2</mn>
</msup>
</mrow>
Этот пример демонстрирует использование различных элементов
представления. Первый элемент, очень широко используемый, это элемент mrow.
Он используется для обозначения ряда данных с выравниванием по горизонтали. Данные,
содержащиеся между тегами <mrow> и </mrow>
рассматриваются как аргумент элемента mrow. Таким
образом, в элементе mrow содержится целое выражение. Как было замечено
ранее, большинство математических выражений состоят из подвыражений. Эти
подвыражения, в свою очередь, также содержатся в элементе mrow.
Например, a + b также содержится в mrow.
Элемент mfenced используется для
ограничения формул различными типами скобок. По умолчанию используются круглые
скобки.
Обратите внимание на использование элемента mi
для отображения переменных a и b и элемента mo для
выделения оператора +.
Элемент msup применяется в
выражениях с верхними индексами и имеет два аргумента: основание (в нашем
случае (a+b)) и показатель (в нашем случае 2).
Разметка содержания для того же примера будет иметь вид:
<mrow>
<apply>
<power/>
<apply>
<plus/>
<ci>a</ci>
<ci>b</ci>
</apply>
<cn>2</cn>
</apply>
</mrow>
Элемент apply обозначает
применение операции к выражению. В нашем примере применяются пустой
элемент power (для возведения в степень) и аналогичный
элемент plus (для сложения). Обратите внимание, что оба
оператора имеют два аргумента. Но если в случае возведения в степень их порядок
важен лишь отчасти, то в случае применения apply он имеет
ключевое значение, так как первый дочерний элемент является оператором,
принимающим остальные в качестве аргумента.
Обратите внимание на использование элемента ci
для выделения переменных a и b, и элемента cn для
выделения числа 2.
Разметка представления MathML состоит из приблизительно 30
элементов, которые имеют более 50 атрибутов. Большинство элементов представляют
из себя схемы форматирования, которые содержат в себе другие элементы
представления. Каждая схема соответствует двумерному фрагменту нотации, такому
как верхний или нижний индекс, дробь или таблица. Кроме того, в разметке
представления есть описанные выше токены mi, mo
и mn и несколько других, которые используются не так
часто. Несколько оставшихся элементов представления - это пустые элементы,
связанные, в основном, с выравниванием.
Все схемы форматирования делятся на несколько классов. Одна
группа элементов отвечает за индексы и содержит такие элементы, как msub
munder, и mmultiscripts.
Другая отвечает за более общее форматирование и включает элементы mrow,
mstyle и mfrac. Третья
группа реализует работу с таблицами. Элемент maction
образует еще одну категорию и позволяет кодировать различные типы действий над
нотацией, встречающиеся в выражениях, которые toggles between two pieces of
notation.
Схемы форматирования обладают важным свойством: важен
порядок их дочерних элементов. Например, первый дочерний элемент схемы mfrac
является числителем дроби, а второй - знаменателем. Так как порядок дочерних
элементов не задается на уровне XML с помощью MathML DTD, информация о порядке
доступна только препроцессору MathML, в отличие от общего препроцессора XML. Когда
мы хотим подчеркнуть, что элементы MathML, такие как mfrac,
требуют указания дочерних элементов в определенном порядке, мы рассматриваем их
как аргументы, а mfrac - как 'конструктор' нотации.
Разметка содержания содержит около 120 элементов,
принимающих около дюжины атрибутов. Большинство этих элементов - пустые,
соответствующие различным математическим операторам, зависимостям и функциям. В
качестве примера можно привести partialdiff, leq
и tan. Другие, такие как matrix и set,
используются для представления различных типов математических данных. Третья
важная категория элементов разметки содержания, такая как apply,
используется для применения к выражениям операций и создания новых
математических объектов.
Возможно, одним из наиболее важных элементов содержания
является apply. Он используется для применения функции или
операции к набору аргументов. Здесь также важно положение дочерних элементов: первый
дочерний элемент указывает применяемую функцию, остальные - аргументы в
соответствующем порядке. Надо отметить, что конструкция apply
всегда использует префиксную нотацию, как язык программирования LISP. В
частности, даже бинарные операторы, такие как вычитание, описываются
применением префиксного оператора вычитания к двум аргументам. Например, a - b будет описано так:
<mrow>
<apply>
<minus/>
<ci>a</ci>
<ci>b</ci>
</apply>
</mrow>
Многие функции и операции, для того чтобы четко
определенными, требуют одного или нескольких кванторов. Например, кроме подинтегрального
выражения у определенного интеграла должны быть заданы пределы интегрирования и
переменная, по которой происходит интегрирование. По этой причине существует
несколько схем-спецификаторов вроде bvar и lowlimit.
Они используются с операторами diff и int.
Конструкция declare особенно важна для
разметки содержания, которая может обрабатываться системами компьютерной
алгебры. Элемент declare реализует основной механизм присваивания,
когда может быть объявлена переменная определенного типа с определенным
значением.
И в примерах разметки представления, и в примерах разметки
содержания математические выражения рекурсивно разлагаются на вложенные, более
простые элементы MathML, определяющие стадию декомпозиции. В следующем разделе
это проиллюстрировано на более сложных примерах.
Для разных типов задач различные типы разметки могут быть
наиболее подходящими. Документы, созданные до широкого распространения Сети,
очень часто предназначены только для визуального обмена информацией и наилучшим
образом преобразуются в чистую разметку представления, так как семантическая
информация, которую подразумевал автор, может быть восстановлена только
эвристически. Наоборот, некоторые математические приложения и средства обучения
основаны на содержании. Большинство же приложений находятся посредине между
этими крайностями. Для них наиболее подходящим вариантом является объединение
разметки представления и содержания.
Правила объединения разметки представления и содержания
следуют из общего принципа, что смешанная разметка может быть только в тех
местах, где она действительно необходима. Для разметки содержания, встроенной в
разметку представления, это означает, что любые фрагменты содержания должны
быть семантически значимыми и не требовать дополнительных аргументов или
кванторов для того, чтобы быть четко определенными. Для разметки представления,
встроенной в разметку содержания, это означает, что разметка представления
должна содержаться в токене разметки содержания как неделимый элемент,
используемый в качестве имени переменной или функции.
Другой способ заключается в использовании элемента semantics.
Он используется для связывания выражений MathML и различных типов примечаний. Чаще
всего элемент semantics используется для того, чтобы присоединить
фрагмент разметки содержания к разметке представления как семантическое
примечание. Таким образом, автор может определить нестандартную нотацию,
которая будет использоваться при отображении конкретного выражения. Другим
применением элемента semantics является включение других семантических
спецификаций, таких как OpenMath выражения, в выражения MathML. В этом случае,
элемент semantics может быть использован для расширения
разметки содержания MathML.
Все вышесказанное относится к отдельным формулам вне
контекста документа. Давайте подробно рассмотрим пример, соответствующий
примеру "Hello, World!", разбираемому при изучении языков
программирования. Мы представим полный код документа XHTML 1.0, содержащего
рассмотренный выше квадрат суммы двух переменных:
<html xmlns="http://www.w3.org/1999/xhtml"
lang="en" xml: lang="en">
<head>
<title>MathML's Hello
Square</title>
</head>
<body>
<p> This is a perfect square: </p>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mrow>
<msup>
<mfenced>
<mrow>
<mi>a</mi>
<mo>+</mo>
<mi>b</mi>
</mrow>
</mfenced>
<mn>2</mn>
</msup>
</mrow>
</math>
</body>
</html>
Это стандартная структура документа XHTML. Он начинается
открывающим тегом <html>, содержащим декларацию пространства
имен XML и объявление языка. Элемент head содержит, как обычно, заголовок. Открывающий тег <body> beginning also has a
namespace declaration of an abbreviative prefix letter m
to be used for the standard MathML namespace. Затем идет обычный
параграф. И, наконец, идет элемент math, который также
имеет декларацию пространства имен. Внутри элемента math
находится разметка MathML.
1.6 Примеры MathML
Далее мы будем приводить примеры в форме фрагментов разметки
MathML, которые в реальном документе расположены в элементе math.
Нотация: x2 + 4x + 4 = 0.
Разметка:
<mrow>
<mrow>
<msup>
<mi>x</mi>
<mn>2</mn>
</msup>
<mo>+</mo>
<mrow>
<mn>4</mn>
<mo>⁢ </mo>
<mi>x</mi>
</mrow>
<mo>+</mo>
<mn>4</mn>
</mrow>
<mo>=</mo>
<mn>0</mn>
</mrow>
Обратите внимание на использование вложенных элементов mrow
для обозначения термов. Например, левая часть уравнения является операндом для
'='. Выделение термов значительно улучшает структуру для визуального
отображения, воспроизведения с помощью голоса и переноса строк. Символ MathML InvisibleTimes
применяется для того, чтобы сообщить программе отображения, что между 4 и x
запрещен перенос строки. На самом деле, такое использование данного элемента,
введенного еще в MathML 1.0, не рекомендуется. Все обычные текстовые данные
задаются кодами Unicode. Тем не менее, хотя символ для замены ⁢
ожидается в Unicode 3.2, и рассматриваются предложения по
улучшению Unicode, в текущей версии Unicode 3.0 такого символа не используется.
Мы можем использовать ожидаемую цифровую ссылку ࠎ но для понятности
будем продолжать использовать в примерах элемент InvisibleTimes.
Разметка:
<mrow>
<mi>x</mi>
<mo>=</mo>
<mfrac>
<mrow>
<mrow>
<mo>-</mo>
<mi>b</mi>
</mrow>
<mo>± </mo>
<msqrt>
<mrow>
<msup>
<mi>b</mi>
<mn>2</mn>
</msup>
<mo>-</mo>
<mrow>
<mn>4</mn>
<mo>⁢ </mo>
<mi>a</mi>
<mo>⁢ </mo>
<mi>c</mi>
</mrow>
</mrow>
</msqrt>
</mrow>
<mrow>
<mn>2</mn>
<mo>⁢ </mo>
<mi>a</mi>
</mrow>
</mfrac>
</mrow>
Элементы mfrac и msqrt
используются для создания дроби и квадратного корня соответственно.
Обратите внимание, что знак 'плюс-минус' задается
специальной сущностью ±, хотя в данном случае существует
такой символ Unicode, как �B1;. MathML предоставляет обширный список
имен элементов, задающих математические символы. В дополнение к математическим
символам для вывода документа на экран и на печать, MathML предоставляет
символы для воспроизведения документа с помощью речи. Для воспроизведения с
помощью речи важно автоматически определять, как должен быть прочитан фрагмент
<mrow>
<mi>z</mi>
<mfenced>
<mrow>
<mi>x</mi>
<mo>+</mo>
<mi>y</mi>
</mrow>
</mfenced>
</mrow>
Как 'z умножить на величину x плюс y'
or 'z умножить на x плюс y'. Символы ⁢
(U+2062) и ⁡ (U+2061) предоставляют авторам
способ напрямую кодировать такие различия для программ речевого воспроизведения.
Например, в первом случае, символ ⁢ (U+2062)
должен быть вставлен после строки, содержащей z. MathML также содержит
такие сущности как ⅆ (U+2146), представляющая дифференциал. При
печати она отображается с отличными от обычного символа 'd' интервалами, а
произноситься может как 'd' или 'with respect to'. Пока для исключения
двусмысленности используются теги содержания или любой другой механизм, авторы
всегда должны использовать описанные выше символы как сущности для того, чтобы
сделать документы более доступными.
Разметка:
<mrow>
<mi>A</mi>
<mo>=</mo>
<mfenced open=" [" close="]
">
<mtable>
<mtr>
<mtd><mi>x</mi></mtd>
<mtd><mi>y</mi></mtd>
</mtr>
<mtr>
<mtd><mi>z</mi></mtd>
<mtd><mi>w</mi></mtd>
</mtr>
</mtable>
</mfenced>
</mrow>
Элемент mtable указывает на начало
таблицы в MathML. Элемент mtr определяет строку таблицы и элемент mtd
содержит данные для элемента строки (ячейки). Большая часть элементов имеет
атрибуты, определяющие свойства отображения на экране и на печати. Например, у
элемента mfenced есть атрибуты, определяющие, какие символы
должны использоваться в начале и в конце группируемого выражения. Атрибуты
элементов-операторов устанавливаются в определенное справочником значение по
умолчанию при помощи элемента <mo>.
Нотация: x2 + 4x + 4 = 0.
<mrow>
<apply>
<eq/>
<apply>
<plus/>
<apply>
<power/>
<ci>x</ci>
<cn>2</cn>
</apply>
<apply>
<times/>
<cn>4</cn>
<ci>x</ci>
</apply>
<cn>4</cn>
</apply>
<cn>0</cn>
</apply>
</mrow>
Обратите внимание, что элемент apply
используется для уравнений, операторов и функций.
Разметка содержания MathML не содержит элемента для
отображения операции 'плюс-минус'. Поэтому мы используем элемент mo
для объявления, что мы хотим применить разметку представления для этого
оператора в качестве оператора содержания. Это простой пример того, как
разметки представления и содержания могут быть объединены для расширения
разметки содержания.
Нотация:
Разметка:
<mrow>
<apply>
<eq/>
<ci>A</ci>
<matrix>
<matrixrow>
<ci>x</ci>
<ci>y</ci>
</matrixrow>
<matrixrow>
<ci>z</ci>
<ci>w</ci>
</matrixrow>
</matrix>
</apply>
</mrow>
Здесь мы используем элементы matrix и matrixrow
для помещения содержания в строку матрицы. Заметьте, что по умолчанию
отображение элемента содержания matrix включает в себя
ограничивающие круглые скобки, а, значит, нет необходимости кодировать их
вручную. В этом состоит отличие от элемента представления mtable,
который может и не относиться к матрице, и, следовательно, требует отдельного
указания, что надо использовать скобки.
1.6.3 Примеры смешанной
разметки
Нотация: 
Разметка:
<mrow>
<semantics>
<mrow>
<msubsup>
<mo>∫ </mo>
<mn>1</mn>
<mi>t</mi>
</msubsup>
<mfrac>
<mrow>
<mo>ⅆ </mo>
<mi>x</mi>
</mrow>
<mi>x</mi>
</mfrac>
</mrow>
<annotation-xml encoding="MathML-Content">
<apply>
<int/>
<bvar><ci>x</ci></bvar>
<lowlimit><cn>1</cn></lowlimit>
<uplimit><ci>t</ci></uplimit>
<apply>
<divide/>
<cn>1</cn>
<ci>x</ci>
</apply>
</apply>
</annotation-xml>
</semantics>
</mrow>
В этом примере мы используем элемент semantics
для того, чтобы представить выражение разметки содержания MathML как
семантическое примечание к выражению разметки представления. В представленной
разметке элемент msubsup применяется для задания нижних и верхних
индексов в выражении, в данном случае - пределов интегрирования в определенном
интеграле. Также для описания символов интеграла и дифференциала используются
сущности ∫ и ⅆ.
Элемент semantics содержит в
качестве первого дочернего элемента комментируемое выражение, а в качестве
второго - сам комментарий. На тип нотации, задаваемой элементом semantics,
ограничений не существует. Например, можно задавать разметку TEX или
компьютерной алгебры в качестве примечания. Тип аннотации задается атрибутом encoding
и элементами annotation, annotation-xml.
Элемент semantics также часто
применяется, когда надо задать предложения по представлению разметки содержания
документа. В этом случае, в применении к вышеописанной формуле мы получим такую
разметку:
<semantics>
<apply>
<int/>
<bvar><ci>x</ci></bvar>
<lowlimit><cn>1</cn></lowlimit>
<uplimit><ci>t</ci></uplimit>
<apply>
<divide/>
<cn>1</cn>
<ci>x</ci>
</apply>
</apply>
<annotation-xml encoding="MathML-Presentation">
<mrow>
<msubsup>
<mo>∫ </mo>
<mn>1</mn>
<mi>t</mi>
</msubsup>
<mfrac>
<mrow>
<mo>ⅆ </mo>
<mi>x</mi>
</mrow>
<mi>x</mi>
</mfrac>
</mrow>
</annotation-xml>
</semantics>
Этот тип комментариев полезен, если требуется отображение
разметки содержания, отличное от заданного по умолчанию. Например, по
умолчанию, некоторые программы отображения могут выводить подинтегральное
выражение в виде ' (1/x) dx'. С помощью комментария
MathML-Presentation можно задать отображение в виде 'dx/x'. Будьте
внимательны, так как программы отображения не обязаны принимать во внимание
расположенную в комментариях информацию. Ее использование зависит от программы.
MathML основан на [XML] (Extensible Markup Language), а
значит его синтаксис подчиняется правилам сиснтаксиса XML, и грамматика
определяется DTD (Document Type Definition). Другими словами, детали
использования тегов, атрибутов, сущностей и всего остального определены в
спецификации языка XML, а детали, касающиеся элементов и атрибутов MathML,
вложенности элементов и так далее, определены в MathML DTD.
W3C, стараясь увеличить легкость и гибкость использования
XML в Сети и поддержать создание модульных XML-приложений, обнаружил, что
основная форма DTD не является достаточно гибкой. Поэтому, была создана рабочая
группа W3C для разработки XML Schemas, которые являются документами
спецификации и должны заменить DTD. MathML 2.0 разработан так, что математики
могли использовать все преимущества развивающихся Web-технологий. Таким
образом, существует схема для MathML.
Также MathML определяет синтаксические и грамматические
правила в дополнение к общим правилам, которые он наследует как приложение XML.
Эти правила позволяют MathML представлять значительно больше информации, чем
возможно представить с помощью чистого XML, без введения большого числа новых
элементов и использовать значительно более сложные DTD или схемы. Конечно,
недостатком введения специфических правил MathML является то, что созданные
документы не могут обрабатываться процессорами и валидаторами XML.
Существует два основных типа дополнительных грамматических и
синтаксических правил MathML. Первый тип включает в себя установку
дополнительных критериев на значения атрибутов. Например, в чистом XML
невозможно потребовать, чтобы значение атрибута было положительным целым числом.
Второй тип правил определяет более детальные ограничения на дочерние элементы (например,
на их порядок), чем даны в DTD или даже схемах. Например, в XML нельзя указать,
что первый дочерний элемент должен обрабатываться иначе, чем остальные.
1.7.2 Пример
синтаксиса XML
Так как MathML основан на XML, спецификация MathML использует
терминологию XML. Данные XML состоят из символов Unicodes (которые включают в
себя обычные ASCII-символы), ссылки на сущности (неформально называемые
сущностями), такие как <, которые обычно представляют расширенные
символы, и элементы, такие как <mi fontstyle="normal">
x </mi>.
Элементы часто содержат в себе другие XML-данные, называемые
их 'содержанием' или 'телом', между 'открывающим' и 'закрывающим' тегами, также
как в HTML. Существуют также 'пустые элементы', такие как <plus/>,
у которых открывающий тег заканчивается символом />,
чтобы показать, что элемент не имеет содержания или закрывающего тега. Открывающий
тег должен содержать именованные параметры, называемые атрибутами, например, fontstyle="normal"
в приведенном выше примере.
Так как большие и маленькие буквы различаются в XML, то и
имена элементов и атрибутов MathML являются чувствительными к регистру. Для
удобочитаемости в спецификации MathML большинство из них определены в нижнем
регистре.
В формальном обсуждении разметки XML делается различие между
элементом, таким как mrow и задающими его тегами <mrow>
и </mrow>. То, что находится между тегами <mrow>
и </mrow>, называется содержанием или телом
элемента mrow. 'Пустой элемент', например none,
не имеет тела и определяется одним тегом вида <none/>.
В этой спецификации не будет делаться упора на это различие между тегами и
элементами. Например, мы иногда будем ссылаться на элементы <mrow>
и <none/>, подразумевая элемент, которому
принадлежат эти теги. Это делается для того, чтобы ссылки на элементы
отличались от ссылок на атрибуты. Тем не менее, термины 'элемент' and 'тег'
будут использоваться в строгом соответствии с терминологией XML.
Многие элементы MathML требуют определенного числа дочерних
элементов или присваивают дополнительный смысл дочерним элементам, стоящим в
определенной позиции. Как было отмечено выше, этот тип ограничений является
специфическим для MathML и не может быть задан при помощи синтаксиса и
грамматики XML. Когда дочерний элемент данного элемента MathML удовлетворяет
этим дополнительным условиям, мы будем говорить о нем как об аргументе,
а не о дочернем элементе, чтобы подчеркнуть специфичность его использования. Заметьте,
что термин 'аргумент' применяется именно в этом техническом смысле, если не
указано обратное.
Некоторые элементы имеют другие требования на число или тип
аргументов. Эти дополнительные требования описываются для каждого конкретного
элемента.
В соответствии со спецификацией языка XML, атрибуты
элементов должны быть заданы в одной из следующих форм:
attribute-name = "value"
or
attribute-name = 'value'
где пробелы вокруг знака '=' необязательны.
Имена атрибутов выделены в тексте спецификации моноширинным
шрифтом, так же как и примеры.
Значения атрибутов, которые в MathML могут быть строкой
произвольных символов, должны быть заключены в двойные (")
или одинарные (') кавычки. Значение атрибута может содержать тот
тип кавычек, который не используется для заключения всего значения.
MathML использует более сложный синтаксис для значений
атрибутов, чем общий синтаксис XML, задаваемый MathML DTD. Эти дополнительные
правила предназначены для приложений MathML, и их нарушение является ошибкой
MathML, однако они не могут быть отслежены процессорами XML. Синтаксис значений
элементов MathML определен в таблице атрибутов и сопровожден описанием каждого
элемента, используя описанную ниже нотацию. Когда приложение MathML
обрабатывает значения атрибутов, все пробелы, за исключением разделяющих
отдельные слова или числа, игнорируются. Символьные данные могут быть включены
в значения атрибутов напрямую или с использованием ссылочных сущностей.
В частности, символы ", ', &
и < могут быть включены в значения атрибутов MathML
(когда это разрешено синтаксисом) с использованием сущностей ",
', & и <,
соответственно.
MathML DTD, объявляет типы большинства значений атрибутов
как строку CDATA. Это позволяет увеличить совместимость с
существующим программным обеспечением на основе SGML и XML и расширять список
предопределенных значений. Подобные же рассуждения применимы к схемам XML.
Для описания MathML-специфического синтаксиса допустимых
значений атрибутов, в этом документе используются следующие соглашения и
нотации.
| Нотация |
Что означает |
| number |
десятичное целое или рациональное число (строка цифр с одной
десятичной точкой), возможно, начинающееся со знака '-' |
| unsigned-number |
десятичное целое или вещественное число, без знака |
| integer |
десятичное целое число, возможно, начинающееся со знака '-' |
| positive-integer |
десятичное целое число, без знака, не 0 |
| string |
произвольная строка (всегда полное значение атрибута) |
| character |
одиночный непробельный символ или ссылочая сущность MathML; возможно
разделение пробелами |
| #rrggbb |
цвет в формате RGB; три пары шестнадцатиричных цифр в примере
#5599dd определяют пропорцию красного, зеленого и синего по шкале от x00 до
xFF, которая дает яркий голубой цвет. |
| h-unit |
единица измерения горизонтальной длины (допустимые единицы
измерения перечислены ниже) |
| v-unit |
единица измерения вертикальной длины (допустимые единицы измерения
перечислены ниже) |
| css-fontfamily |
объясняется ниже, в подразделе о CSS |
| css-color-name |
объясняется ниже, в подразделе о CSS |
| остальные слова, выделенные курсивом |
объясняются в тексте, отдельно для каждого атрибута |
| form + |
один или более экземпляров 'form' |
| form * |
нуль или более экземпляров 'form' |
| f1 f2... fn |
один экземпляр каждой формы, последовательно, возможно
разделенные пробельными символами |
| f1 | f2 |... | fn |
любая из указаных форм |
| [form] |
необязательный экземпляр 'form' |
| (form) |
то же самое, что и просто form |
| невыделенные слова |
слова, включеные в значени атрибута дословно (есди это не часть
объясняющей фразы) |
| символы в кавычках |
символы, дословно включенные в значение атрибута (например,
"+" or '+') |
Приоритет операция, от наивысшего к наинизшему:
form + или form *
f1 f2... fn (последовательность форм)
f1 | f2 |... | fn (одна из форм)
Тип string может содержать произвольные символы,
которые определены в значениях атрибута XML CDATA. В
MathML нет синтаксических правил, по которым string может быть частью
значения атрибута, а не всем значением.
Соседние ключевые слова и числа в значениях атрибутов должны
разделяться пробельными символами, за исключением следующих за числами
идентификаторов единиц измерения (что указано в синтаксисе символов h-unit
и v-unit). Пробельные символы не требуются, но
разрешены между любыми перечисленными выше токенами, за исключением (для
совместимости с CSS) непосредственно перед идентификаторами единиц измерения,
между знаком '-' и числами, между # и rrggbb
или rgb.
Значения числовых атрибутов, которые задают размеры и должны
зависеть от текущего шрифта, могут задаваться в связанных со шрифтом единицах
измерения или в указанных абсолютных единицах (описанных ниже). Горизонтальные
размеры обычно задаются в em, а вертикальные - в ex. Идентификаторы
em или ex следуют
непосредственно за числом. Например, горизонтальные отступы от оператора '+'
обычно задаются в em, хотя могут использоваться и другие единицы
измерения. Использование связанных со шрифтом единиц измерения
предпочтительнее, чем абсолютных, так как они позволяют увеличивать или
уменьшать размер отображаемого элемента в зависимости от текущего размера
шрифта.
Для большинства числовых атрибутов возможные значения
ограничены некоторым подмножеством, другие значения ошибкой не являются (если
не указано противное), а округляются программой отображения вверх или вниз до
ближайшего допустимого. Множество допустимых значений может зависеть от
программы отображения и не определяется MathML.
Если числовое значение в соответствии с синтаксисом атрибута
может содержать знак минус ('-'), например number или integer,
то его использование в случае, когда отрицательные значения не существенны,
ошибкой не является. Вместо этого, значение должно обрабатываться приложением
так, как описано в предыдущем параграфе. Явное указание знака плюс ('+') как
части числового значения запрещено за исключением тех случаев, когда это
специально указано в синтаксисе (в виде '+' или "+"), и его
присутствие может изменить смысл значения атрибута (как описано в каждом из
таких атрибутов).
Символы h-unit, v-unit,
css-fontfamily, и css-color-name
рассматриваются в следующих подразделах.
Некоторые атрибуты принимают горизонтальные и вертикальные
размеры как числа, за которыми следует 'идентификатор единицы измерения' (часто
называемый 'единицей измерения'). Синтаксические символы h-unit
и v-unit относятся к горизонтальным и вертикальным
размерам соответственно. Возможные единицы измерения и размеры, к которым они
относятся, перечислены в таблице, расположенной далее; они совпадают для
горизонтальных и вертикальных размеров, но синтаксические символы отличаются (как
напоминание используемого в них направления).
Идентификаторы единиц измерения и их смысловое значение
взяты из. Тем не менее, синтаксис числа с последующим идентификатором в MathML
не идентичен синтаксису в CSS, так как числа в CSS не могут заканчиваться
десятичной точкой и могут начинаться со знака '+'.
Допустимые горизонтальные и вертикальные единицы измерения в
MathML:
| Идентификатор |
Описание |
| em |
em (единица измерения, зависящая от размера шрифта и обычно
применяемая для горизонтальных размеров) |
| ex |
ex (единица измерения, зависящая от размера шрифта и обычно
применяемая для вертикальных размеров) |
| px |
пиксель |
| in |
дюйм (1 дюйм = 2.54 сантиметра) |
| cm |
сантиметр |
| mm |
миллиметр |
| pt |
пункт (1 пункт = 1/72 дюйма) |
| pc |
picas (1 pica = 12 пунктов) |
| % |
процент от величины |
Типографские единицы измерения em и ex
обсуждаются далее в пункте 'Дополнительные замечания'.
% является 'относительной единицей измерения'; когда
значение атрибута задано в виде n% (для любого числового
значения n), значение определяется как значение по умолчанию,
умноженное на n и поделенное на 100. Значение по умолчанию (или
способ, которым его можно получить, если оно не является константой) описано в
таблице атрибутов для каждого элемента, а его смысл описан в последующей
документации по атрибуту. (Элемент mpadded имеет
свой синтаксис для% и не позволяет использовать его как идентификатор единицы
измерения)
Для согласованности с CSS, единицы измерения длины в MathML
могут быть необязательными. Когда это так, символ единицы измерения в
синтаксисе атрибута заключается в квадратные скобки, например, число
[h-unit]. Смысл значения атрибута без единиц измерения описан в
документации для каждого атрибута; обычно указанное число умножается на
значение по умолчанию. (В этом случае число nnn без
единицы измерения эквивалентно числу nnn умноженному
на 100 и со знаком %. Например, <mo maxsize="2"> (</mo>
эквивалентно <mo maxsize="200 %"> (</mo>)
Как исключение (тоже для совместимости с CSS), числовые
значения равные нулю не требуют указания идентификатора единицы измерения даже
если этого требует синтаксис. В этом случае наличие или отсутствие
идентификатора единицы измерения не играет роли, так как любое число умноженное
на 0 есть 0.
Для большинства атрибутов в данной спецификации в качестве
стандартных единиц измерения выбраны единицы, используемые в типографском
наборе; когда не указано конкретное значение величины, то стандартные единицы
измерения обычно указаны в таблице или в описании атрибута. Чаще всего
используются такие единицы измерения как em или ex.
Однако, могут использоваться любые единицы, если в описании конкретного
атрибута не указано обратное.
Отметим, что некоторые атрибуты, например framespacing
в <mtable>, могут содержать более одного
числового значения, после каждого из которых следует своя единица измерения.
Принято использовать единицы измерения ex
в основном для задания вертикальных размеров, а em - для горизонтальных,
хотя это не является обязательным требованием. Эти единицы измерения зависят от
шрифта, используемого для отображения элемента, в атрибутах которого они применяются,
и его размера. А значит, они должны интерпретироваться после таких
атрибутов, как fontfamily и fontsize, если
они встречаются в одном элементе, так как изменение текущего шрифта или его
размера может привести к изменению размера единиц измерения.
Определение длины каждой единицы измерения (но не синтаксис
MathML для значений длины) такое же как в CSS, за исключением тех случаев,
когда шрифт устанавливает специальные значения для em
и ex, отличающиеся от значений, определенных в CSS (font
size и 'x'-height соответственно).
Некоторые атрибуты MathML, перечисленные ниже, соответствуют
свойствам отображения текста, определенным в CSS1. Это сделано для того, чтобы
программы отображения могли запросить CSS-окружение о соответствующих свойствах
при определении значений атрибутов по умолчанию.
Возможность определения стилевых свойств через атрибуты MathML
и CSS имеет и недостатки. Как минимум, это запутывает, а в худшем случае, это
приводит к непреднамеренному изменению смысла уравнений при изменении CSS для
всего документа. Поэтому, эти атрибуты осуждаются. В свою очередь, MathML 2.0
вводит четыре новых математических стилевых атрибута. Эти атрибуты используют
логические значения для того, чтобы лучше передать абстрактные категории
используемых в математике символов, и предоставляют четкое разделение между
MathML и CSS.
Следующая таблица показывает соответствие осуждаемых
стилевых атрибутов MathML 1.01 и их CSS-аналогов:
| Атрибут MathML |
Свойство CSS |
синтаксический символ |
Элемент MathML |
| fontsize |
font-size |
- |
токены представления; mstyle
|
| fontweight |
font-weight |
- |
токены представления; mstyle
|
| fontstyle |
font-style |
- |
токены представления; mstyle
|
| fontfamily |
font-family |
css-fontfamily |
токены представления; mstyle
|
| color |
color |
css-color-name |
токены представления; mstyle
|
| background |
background |
css-color-name |
mstyle
|
Порядок обработки атрибутов и стилевых таблиц.
CSS или аналогичные стилевые таблицы могут задавать
изменения свойств отображения элементов MathML. Так как свойства отображения
могут изменяться как атрибутами элемента, так и программой отображения,
необходимо определить порядок, в котором происходят изменения из разных
источников. Примером автоматического согласования является ситуация с fontsize.
В случае 'абсолютных' изменений, например, установки нового
значения свойства, независимого от старого значения (в отличие от
'относительных' изменений, таких как инкремент или умножение на число),
действуют только последние абсолютные изменения, поэтому источник изменений с
наивысшим приоритетом должен обрабатываться последним.
В случае CSS, порядок обработки изменений, действующих на
свойства отображения элемента MathML, из различных источников должен быть
следующим: (изменяется первым; самый низкий приоритет)
Автоматические изменения свойств или атрибутов, основанных
на типе родительского элемента и положении элемента в родительском (как
упоминается выше об изменениях fontsize в соответствии с scriptlevel;
такие изменения обычно применяются самим родительским элементом перед передачей
свойств отображения текущему элементу
Из стилевых таблиц читателя: стили, которые не
объявлены 'важными'
Явно заданные атрибуты текущего элемента MathML
Из стилевых таблиц автора: стили, которые не
объявлены 'важными'
Из стилевых таблиц автора: стили, которые объявлены
'важными'
Из стилевых таблиц читателя: стили, которые объявлены
'важными' (изменяется последним; самый высокий приоритет).
Отметим, что порядок изменений, производимых стилевыми
таблицами CSS, определен в самих CSS (это порядок, определяемый CSS2). Следующее
объяснение относится только к случаю, когда в этом порядке происходят
изменения, вызванные точным заданием атрибутов MathML.
Объяснение: Атрибуты отображения в MathML аналогичны
атрибутам отображения в HTML (таким как align),
которые, согласно определенному в CSS порядку, должны обрабатываться с
одинаковым приоритетом. Более того, такой выбор очередности позволяет читателям
решить, определяя стили CSS 'важными', какие из их установок должны
переопределять явные установки MathML. Так как выражения MathML, состоящие из
элементов содержания или представления, в первую очередь предназначены для
передачи смысла, а 'графическое представление' (если таковое имеется) должно
помогать этому (но не является важным само по себе), вероятно, что читатели
захотят, чтобы их стилевые предпочтения имели приоритеты. Основным исключением
является ситуация, когда атрибуты отображения предполагают изменение смысла
выражения.
Значения по умолчанию для атрибутов MathML как правило
даются вместе с подробным описанием соответствующего элемента. Значения по
умолчанию, указанные в таблицах атрибутов обычным шрифтом, являются точными (если
они не являются очевидными объяснениями), выделенные курсивом фрагменты
описывают, как значения по умолчанию могут быть вычислены.
Значения по умолчанию, описанные как inherited, берутся из
среды отображения, как описано для mstyle, или, в
некоторых отдельно описанных случаях, из значений других атрибутов окружающих
элементов, или из определенной части этих значений. Всегда используется
значение, которое может быть задано точно, если оно известно; оно никогда не
зависит от содержания или атрибутов данного элемента, только от его окружения.
(Его смысл при использовании может, тем не менее, зависеть от этих атрибутов
или содержания)
Значения по умолчанию, описанные как automatic, должны
вычисляться программой отображения таким образом, чтобы получить
высококачественное изображение. Способ, как этого добиться, обычно не указан в
спецификации MathML. Всегда используется значение, которое может быть задано
точно, если оно известно; но оно обычно зависит от содержания элемента и,
возможно, от среды отображения.
Другие выделенные курсивом описания значений по умолчанию,
которые встречаются в таблицах атрибутов, объясняются отдельно для каждого
атрибута.
Одинарные или двойные кавычки, в которые должны быть
заключены значения атрибута, расположенного в открывающем теге XML, не показаны
в синтаксисе значений в таблице атрибутов, но показаны в тексте примеров.
Отметим, что, как правило, не существует значений, которые
точно могут быть присвоены атрибутам MathML и имитируют эффект их отсутствия
для атрибутов, являющихся inherited или automatic. Указание 'inherited' или
'automatic' точно не будет работать, и вообще запрещено. Более того, даже для
атрибутов представления (для которых здесь приведены конкретные значения по
умолчанию), должен использоваться элемент mstyle для
изменения содержащихся в нем элементов. Поэтому, MathML DTD определяет
большинство значений по умолчанию для атрибутов представления как #IMPLIED,
что не позволяет обработчикам XML добавлять к этим атрибутам любые специальные
значения по умолчанию. MathML schema работает по тем же правилам.
В XML DTD, разрешенные значения атрибутов могут быть
определены как общие строки, или могут быть различными способами ограничены (перечислением
возможных значений, или указанием определенного типа данных). Выбор типа
атрибута XML влияет на объем, в котором могут быть проведены проверки
корректности с использованием DTD.
MathML DTD определяет формальные типы атрибутов XML для всех
атрибутов MathML, включая в некоторых случаях перечисления допустимых значений.
В общем, тем не менее, MathML DTD является относительно нестрогим, часто
определяя значения атрибутов как строки; это сделано для совместимости с
парсерами SGML, которые допускают, чтобы несколько атрибутов одного элемента
MathML принимали одинаковые значения (такие как true и false),
и для того, чтобы позволить расширять список предопределенных значений.
В то же время, даже если значение атрибута может быть
определено как строка в DTD, только определенные значения являются допустимыми
в MathML, как описано выше и в оставшейся части этой спецификации. Например,
многие атрибуты требуют числовых значений. В следующем разделе описаны
допустимые значения атрибутов для каждого элемента. Тем не менее, недостаток
жесткости требований в DTD не подразумевает, что эти требования не являются
частью MathML, или что они не могут быть усилены конкретной программой
отображения MathML.
Более того, MathML DTD предоставляется для удобства; хотя и
подразумевается полная совместимость с текстом спецификации, текст должен быть
определяющим в случае возникновения противоречий.
Для того чтобы облегчить использование таких стилевых
механизмов, как XSLT и CSS2, все элементы MathML имеют атрибуты class,
style, и id в
дополнение к атрибутам, описанным для каждого элемента. Программы отображения
MathML, не поддерживающие CSS, могут игнорировать эти атрибуты. MathML
определяет значения этих атрибутов как общие строки, даже если стилевые
механизмы имеют для них более строгий синтаксис. Поэтому, любое значение для
них является допустимым в MathML.
Для того чтобы обеспечить совместимость с механизмами
связывания, все элементы MathML имеют атрибут xlink: href.
Все элементы MathML также имеют атрибут xref
для использования в параллельной разметке. id также используется
в этом контексте.
Каждый эдемент MathML, как наследство от MathML 1.0, также
принимает осужденный атрибут other, который
предполагался для передачи нестандартных атрибутов без нарушения MathML DTD. От
программ отображения MathML требуется обработка этого атрибута только в том
случае, если они реагируютя на все нестандартные атрибуты MathML. Тем не менн,
использование атрибута other сильно осуждается, так как в MathML существуют
другие способы передать специфическую информацию.
MathML игнорирует пробельные символы, встречающиеся вне
токенов. Непробельные символы здесь запрещены. Пробельные символы,
встречающиеся в содержании токенов, удаляются на концах, то есть удаляются все
пробельные символы в начале и конце содержания. Пробельные символы,
расположенные внутри содержания элементов MathML свертываются кононически, то
есть каждая последовательность из 1 или более таких символов заменяется на 1 (иногда
называемый пустым символом).
В MathML, как и в XML, под пробельными символами
подразумеваются простой пробел, табуляция, новая строка или перевод строки, то
есть символы с кодами Unicode U+0020, U+0009,
U+000A, U+000D
соответственно.
Например,
<mo> (</mo> эквивалентно <mo>
(</mo>, и
<mtext>
Теорема
1:
</mtext>
эквивалентно <mtext>Теорема 1: </mtext>.
Авторы, желающие поместить пробельные символы в начале или
конце содержания токена, или последовательность более чем из одного пробельного
символа так, чтобы они не были проигнорированы, должны использовать
или другие неотображаемые пробельные символы. Например, сравните
<mtext>
Теорема
1:
</mtext>
с
<mtext>
Теорема 1:
</mtext>
Когда отображается первый пример, перед словом 'Теорема' нет
пробельных символов, один - между 'Теорема' и '1: ', и нет после '1: '. Во
втором примере одиночный пробел будет отображен перед словом 'Теорема', два - перед
'1: ', и ни одного после '1: '.
Отметим, что атрибут xml: space в
данной ситуации неприменим, так как процессоры XML передают пробельные символы
в токенах процессору MathML; удаление происходит по правилам обработки MathML.
Для пробельных символов, встречающихся вне содержания
токенов mi, mn, mo,
ms, mtext, ci,
cn и annotation, должен
использоваться элемент mspace, в противоположность элементу mtext
содержащий только пробельные символы
В качестве тестового примера для демонстрации возможностей
браузеров была создана простая XHTML-страница, содержащая примеры обоих
разметок. Опишем основные требования к ней. Во-первых, это должны быть
корректным XHTML-документом, то есть:
быть корректным xml-документом;
корневым элементом должен быть элемент html в пространстве
имен XHTML, например:
<html xmlns="http://www.w3.org/1999/xhtml">
должен содержать декларацию типа документа. В нашем случае
это:
<! DOCTYPE html PUBLIC
"- // W3C // DTD XHTML 1.1 plus MathML 2.0 // EN"
"http://www.w3.org/TR/MathML2/dtd/xhtml-math11-f. dtd">
MathML-фрагменты должны принадлежать пространству имен
MathML, например:
<math xmlns="http://www.w3.org/1998/Math/MathML">...
</math>
Тестовый пример, который используется ниже: test. xhtml.
Используемая версия: Mozilla/5.0 (Windows; U; Windows NT 5.0;
en-US; rv: 1.7 5) Gecko/20041107 Firefox/1.0.
Mozilla и построенный на том же ядре Firefox имеют
встроенные возможности отображения разметки MathML. Правда, до сих пор они
ограничены лишь поддержкой разметки представления. Так в нашем тестовом примере
фрагмент разметки представления отобразился правильно, чего нельзя сказать о
разметке содержания.
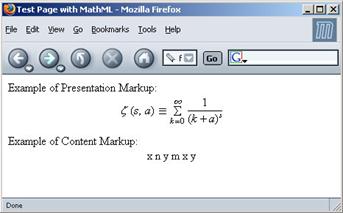
Решением этой проблемы может служить использование
специальных XSLT-стилей "XSLT stylesheets for MathML". Такой подход
возможен, так как поддержка XSLT-трансформаций встроена в браузер. Для этого
надо скачать набор XSLT-стилей и в первой строчке нашей страницы указать ссылку
на заглавный файл mathml. xsl:
<? xml-stylesheet type="text/xsl"
href="mathml. xsl"? >
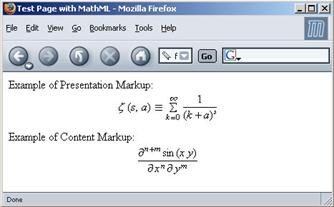
По соображениям безопасности Mozilla позволяет использовать
XSLT-стили расположенные в другом домене просмотра исходного кода MathML с
подсветкой выделенного фрагмента. Правда, при использовании разметки содержания
и XSLT-стилей мы увидим не исходный код, а результат преобразования.
Из других возможностей следует отметить интеграцию с
поисковыми системами. При выделенном фрагменте формулы контекстное меню
позволяет отправить запрос к поисковой системе.
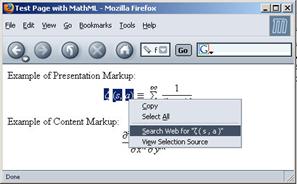
Но пока это задел на будущее, так как пока подобный поиск
результатов не дает.
2.2 Microsoft Internet Explorer
Используемая версия: 6.0.2800.1106 (SP1;
Q867801; Q823353; Q833989)
Браузер от Microsoft не имеет встроенной поддержки MathML. Для
корректного отображения математических формул можно использовать свободно
распространяемый плагин MathPlayer.
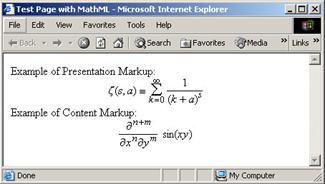
Помимо собственно отображения математической разметки он
позволяет быстро копировать MathML-нотацию. Также можно при желании увеличить
формулу для лучшей наглядности:
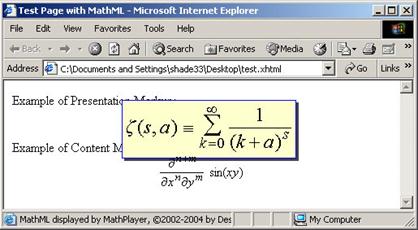
Из недостатков следует отметить отсутствие возможности
выделить или скопировать фрагмент математического выражения. Также нет
возможности (как и в Mozilla) корректно скопировать формулу с окружающим
текстом.
Используемая версия: 7.54u1 (Build 3918; Platform
Win32; System Windows 2000; Java not installed).
Этот браузер на данном своего развития этапе не имеет
возможностей для корректного отображения разметки MathML.
1.
Дорофеев А.В., Федотов А.М. Электронные публикации в среде Internet и
множественность кодировок русского языка // Вычислительные технологии, 1997, т.2,
N 3, c.31-44.
2. Олейник
О.В., Толкачева Е.М., Федотов А.М. Электронные издания и представление
математических текстов на WWW // Вычислительные технологии, 1997, т.2, N 3, c.60-67.
3. Шокин
Ю.И., Федотов А.М., Знаменский С.В. Электронные публикации и проблемы
множественности кодировок русского языка // Информационные технологии и
вычислительные системы, 1997, N 2, c.90-101.
4. Знаменский
С.В. Стандартизация русского TeX: утопия или неизбежность // Вычислительные
технологии, 1997, т.2, N 3, c.51 - 59.
5.
Галактионов В.В. Расширяемый язык разметки XML (Extensible Mark-up
Language): промышленный стандарт, определяющий архитектуру программных средств
Интернет следующего поколения. Сообщение ОИЯИ, Р10-2000-44, Дубна, 2000.
6.
Митюнин В.А. Обзор средств публикации и просмотра математических
документов в сети Интернет - http://mathmag. spbu.ru/article/4/
7. Math on the Web: A Status Report - http://www.dessci.com/ webmath
/status/
8. Including Math Notation in Web Pages - http://mathforum.org/typeseting/
9. MathML 1.01 - http://www.w3.org/TR/REC-MathML/
10. MathML
2.0 - http://www.w3.org/TR/MathML2/
|