Курсовая работа: Анализ и синтез электрических фильтров
Курсовая работа: Анализ и синтез электрических фильтров
Московский Государственный Технический Университет
им. Н.Э. Баумана
Курсовая работа
«Анализ и синтез электрических фильтров»
Калуга
Содержание
1. Задание
2. Разложение периодического сигнала на
гармоники
3. Расчет фильтра
для полосы частот с согласованием его на выходе с сопротивлением нагрузки Rн.
4. Расчет
передаточной функции по напряжению Ku(p), графики АЧХ и
ФЧХ фильтра.
5. Вычислить и
построить график выходного напряжения фильтра при полученном в пункте 2
периодическом входном сигнале.
6. Выполнить расчет переходной
характеристики фильтра и интеграла от нее с учетом
сопротивления нагрузки.
7.Считая, что на входе фильтра действует
одиночный импульс той же формы, что и в пункте 2, вычислить его воздействие и построить график этого отклика.
Сравнить его с выходным сигналом полученным в пункте 5.
8. Вывод
9. Список использованной литературы.
Приложение.
1. Задание
2.
Получить
от преподавателя вариант задания, состоящего из типа фильтра и типа испытательного
сигнала.
3.
Испытательный
сигнал разложить в тригонометрический ряд Фурье, используя пакет MATLAB 6.5(7.0) и m-file: Fourier.m .
4.
Для
заданного варианта рассчитать фильтр, обеспечив его согласование на выходе с сопротивлением нагрузки 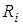 . .
5.
Для полученного
фильтра составить выражение для передаточной функции по
напряжению 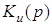 и по ней с помощью пакета MATLAB 6.5(7.0) и m-file: afchx.m вычислить и построить графики АЧХ и ФЧХ. и по ней с помощью пакета MATLAB 6.5(7.0) и m-file: afchx.m вычислить и построить графики АЧХ и ФЧХ.
6.
Вычислить
и построить график выходного напряжения фильтра при полученном в пункте 2 периодическом входном сигнале. При
этом необходимо использовать значения АЧХ и ФЧХ, найденные в пункте 4.
7.
Выполнить
расчет переходной характеристики фильтра и интеграла от нее с учетом сопротивления
нагрузки.
8.
Считая,
что на входе фильтра действует одиночный импульс той же формы, что и в пункте 2, вычислить с помощью интеграла
Дюамеля отклик на его воздействие и построить
график этого отклика. Сравнить его с выходным сигналом, полученным в пункте
5.
9.
Оформить
пояснительную записку в соответствии с установленными требованиями.
Задание:
Таблица 1.1
| № |
Тип
фильтра |
Граничные
частоты |
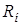 , Ом , Ом
|
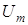 , В , В
|
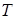 , мс , мс
|
| 0 |
ЗФ типа К,
Г - обр.
с
П-обр.входом
|
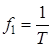 ; ;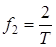
|
1000 |
100 |
80 |
Тип
испытательного сигнала № 8 (рис 1.1)
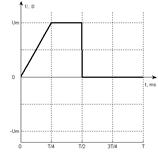
Рис 1.1 Испытательный сигнал
2. Разложение периодического сигнала на гармоники
В
данном случае необходимо разложить периодический сигнал (напряжения) в тригонометрический
ряд Фурье.
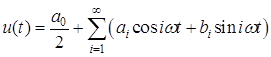 , ,
где
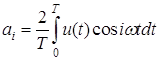 , ,
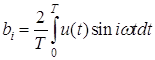 , ,
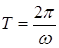 - период, - период,
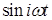 , ,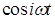 - функции, составляющие
ортогональный базис. - функции, составляющие
ортогональный базис.
Разложение
справедливо для периодических функций (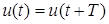 ),
заданных на всей числовой оси ),
заданных на всей числовой оси 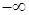 до до 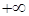 . .
Данную
функцию нельзя разложить в тригонометрический ряд Фурье, так как она не
периодическая. Доопределим данную функцию на всю числовую ось (рис. 2.1). В
данном случае функция не является ни чётной, ни нечётной. Для такого сигнала
справедливо общее разложение, содержащее постоянную составляющую, косинусы и
синусы.
Кроме
периодичности полученная функция удовлетворяет всем условиям теоремы Дирихле:
1.
она непрерывна на отрезке 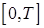 и имеет конечное число
точек разрыва первого рода; и имеет конечное число
точек разрыва первого рода;
2.
она имеет конечное число
экстремумов на этом отрезке.
Следовательно,
к полученной функции можно применить разложение в тригонометрический ряд Фурье.
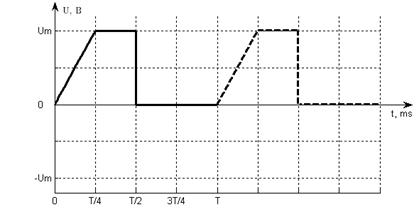
Рис. 2.1
Запишем
аналитическое выражение для данной функции:
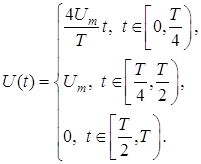
Вычислим
с помощью пакета MATLAB 6.5(7.0) и m-file: Fourier.m коэффициенты Фурье 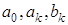 для двадцати гармоник. для двадцати гармоник.
Таблица 2.1
Результатов вычислений:
|
Коэффициенты
Фурье для данной функции
F(x),
заданной графически на отрезке [0,T].
|
|
Коэффициенты
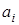
|
Коэффициенты
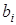
|
|
A(0)= 75.000
A(1)= -20.264
A(2)= -10.132
A(3)= -2.252
A(4)= -0.000
A(5)= -0.811
A(6)= -1.126
A(7)= -0.414
A(8)= -0.000
A(9)= -0.250
A(10)= -0.405
A(11)= -0.167
A(12)= -0.000
A(13)= -0.120
A(14)= -0.207
A(15)= -0.090
A(16)= -0.000
A(17)= -0.070
A(18)= -0.125
A(19)= -0.056
A(20)= -0.000
|
B(1)= 52.095
B(2)= -15.915
B(3)= 8.359
B(4)= -7.958
B(5)= 7.177
B(6)= -5.305
B(7)= 4.134
B(8)= -3.979
B(9)= 3.787
B(10)= -3.183
B(11)= 2.726
B(12)= -2.653
B(13)= 2.568
B(14)= -2.274
B(15)= 2.032
B(16)= -1.989
B(17)= 1.943
B(18)= -1.768
B(19)= 1.619
B(20)= -1.592
|
Частота
первой гармоники: 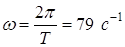 . .
Таким
образом мы получили разложение:
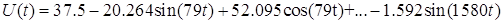 . .
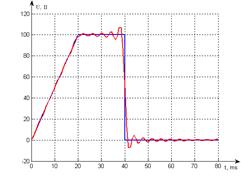
Рис 2.2 График напряжения на
входе
3. Расчет фильтра для полосы частот с
согласованием его на выходе с сопротивлением нагрузки Rн.
Под
электрическим фильтром будем понимать пассивный четырёхполюсник, пропускающий
некоторую определённую полосу частот с малым затуханием и подавляющий все
остальные частоты.
Полоса
частот, для которых затухание мало, называется полосой пропускания или полосой
прозрачности. Остальные частоты составляют полосу подавления или полосу
непрозрачности.
Заградительный
фильтр (ЗФ) - пропускают сигналы в диапазоне частот от 0 до w1 и от w2 до ¥.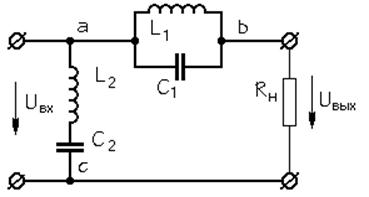
Рис. 3.1 Схема ЗФ
Рассчитаем
параметры элементов фильтра с учётом поставленной задачи:
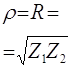 т.е. т.е.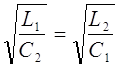
Частота
среза:
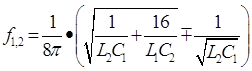 ; ;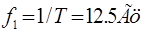 ; ;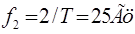 . .
Формулы
для расчета и полученные значения элементов фильтра.
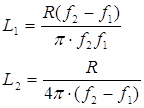 ; ; 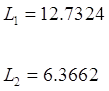 ; ; 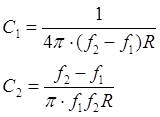 ; ;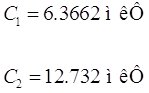 . .
Уточним
полученные параметры по следующим формулам :
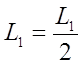 ; ;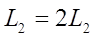 ; ;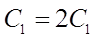 ; ;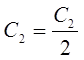 . .
Таким
образом получаем:
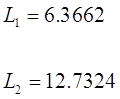 ; ;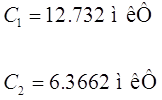
4. Расчет передаточной функции по напряжению Ku(p), графики АЧХ и ФЧХ
фильтра.
Составим
для полученного фильтра выражение для передаточной функции по напряжению K(p).
Для этого нагрузим полученный фильтр со стороны выхода нагрузкой 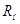 , предполагая что на вход
подается напряжение , предполагая что на вход
подается напряжение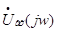 , а на выходе при
этом получается , а на выходе при
этом получается 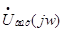 : :
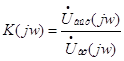 ; ; 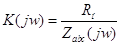
Для
определения передаточной функции найдем комплексные сопротивления:
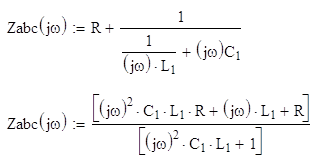
Передаточная
функция приобретает следующий вид:
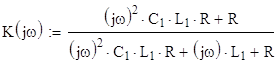
Запишем
передаточную функцию в численном виде(с учетом замены jw на p) :
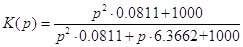
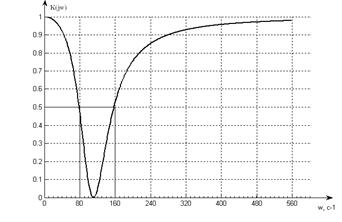
Рис 4.1 График АЧХ.
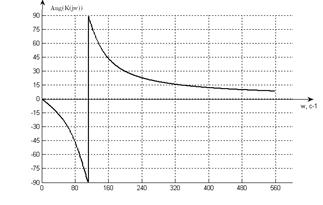
Рис 4.2 График ФЧХ.
Таблица 4.1
Таблица
значений АЧХ и ФЧХ
|
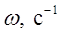
|
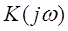
|
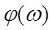
|
|
0.000
10.000
20.000
30.000
40.000
50.000
60.000
70.000
80.000
90.000
100.000
110.000
120.000
130.000
140.000
150.000
160.000
170.000
180.000
190.000
200.000
210.000
220.000
230.000
240.000
250.000
260.000
270.000
280.000
290.000
300.000
310.000
320.000
330.000
340.000
350.000
360.000
370.000
380.000
390.000
400.000
410.000
420.000
430.000
440.000
450.000
460.000
470.000
480.000
490.000
500.000
510.000
520.000
530.000
540.000
550.000
560.000
|
1.000
0.996
0.983
0.959
0.921
0.863
0.775
0.646
0.471
0.264
0.081
0.001
0.046
0.167
0.304
0.427
0.527
0.607
0.669
0.718
0.756
0.788
0.814
0.835
0.852
0.867
0.880
0.891
0.900
0.909
0.916
0.922
0.928
0.933
0.937
0.941
0.945
0.948
0.951
0.954
0.957
0.959
0.961
0.963
0.965
0.967
0.968
0.970
0.971
0.972
0.973
0.975
0.976
0.977
0.977
0.978
0.979
|
0.000
-3.672
-7.497
-11.641
-16.310
-21.765
-28.346
-36.483
-46.639
-59.087
-73.465
-88.471
77.609
65.878
56.516
49.184
43.426
38.847
35.147
32.107
29.570
27.424
25.584
23.990
22.595
21.364
20.268
19.286
18.401
17.598
16.867
16.198
15.583
15.016
14.491
14.003
13.549
13.124
12.727
12.355
12.004
11.674
11.362
11.067
10.788
10.523
10.271
10.031
9.803
9.585
9.377
9.178
8.988
8.806
8.631
8.463
8.302
|
5. Вычислить и построить график выходного напряжения фильтра при
полученном в пункте 2 периодическом входном сигнале.
Для
построения графика выходного напряжения необходимо взять разложение входного
сигнала в ряд Фурье, найти отклики на каждую гармонику входного сигнала, а
затем их сложить.
Отклик
цепи на постоянную составляющую:
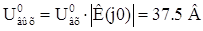
Напряжение
на входе:
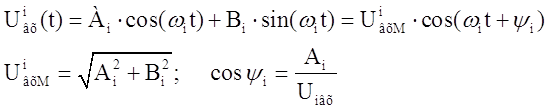
Напряжение
на выходе:
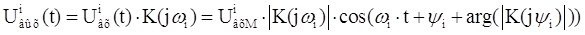
Таким
образом:
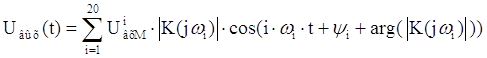
Графики
первых 3-х гармоник напряжения на входе и на выходе показаны на рис 5.1 и 5.2
соответственно.
График
напряжения на входе показан на рис 2.2.
График
напряжения на выходе показан на рис 5.3.
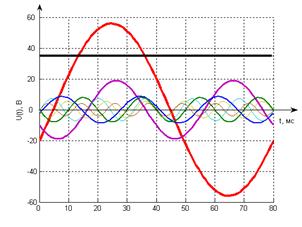
Рис 5.1 7 первых гармоники
напряжения на входе.
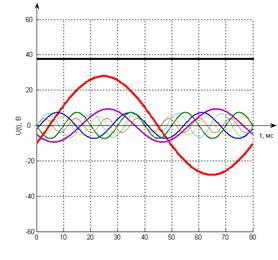
Рис 5.2 7 первых гармоники
напряжения на выходе.
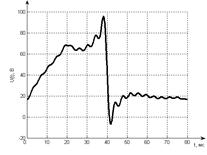
Рис 5.3 Напряжение на выходе
фильтра
6. Выполнить расчет переходной характеристики фильтра и интеграла от нее
с учетом сопротивления нагрузки.
Запишем
выражение для передаточной функции:
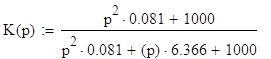
Переходная
функция h(t) имеет своим изображением h(p)=Ku(p)/p при
подаче
на вход единичного ступенчатого воздействия s(t), и нулевых
начальных условиях.
Перейдем
к оригиналу, применим вторую теорему разложения. Подставляя значения корней
характеристического уравнения находим преобразование Лапласа для переходной
характеристики.

h(t)=1-0.7562057.*exp(-39.2962963.*t).*sin(103.93016939.*t)
Построим
график переходной характеристики (рис. 6.1.).
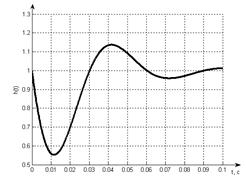
Рис. 6.1 График переходной
характеристики h(t)
Находим
интеграл от переходной характеристики.
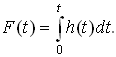
проводя
простое интегрирование(нахождение неопределенного интеграла)
получаем
значение интеграла от переходной характеристики.
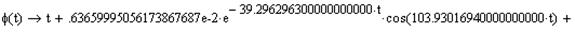
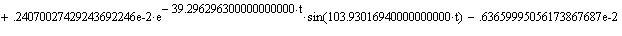
Построим
график интеграла (F(t))от переходной характеристики (h(t))(рис. 6.2.).
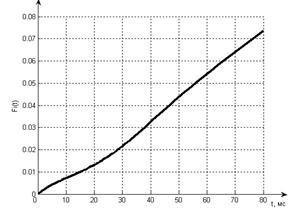
Рис. 6.2 График интеграла (Fi(t))
от переходной характеристики (h(t))
7.Считая, что на входе фильтра действует одиночный импульс той же формы,
что и в пункте 2, вычислить его воздействие и построить график этого отклика.
Сравнить его с выходным сигналом полученным в пункте 5.
Вычислим отклик на
входное воздействие и построим график этого отклика.
График входного
воздействия показан на рис 7.1.
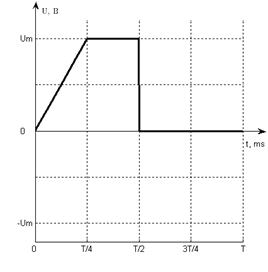
Рис 7.1 Испытательный сигнал.
Выделим в этом сигнале
типовые сигналы:
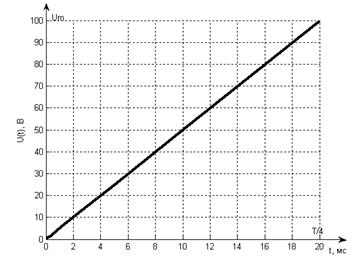
Рис 7.2 Первый типовой сигнал (луч).
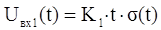 , тогда , тогда 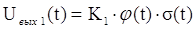 , где , где 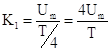 . .
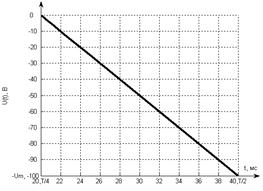
Рис 7.3 Второй типовой сигнал (луч).
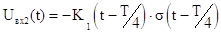 ; тогда ; тогда 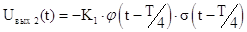 ;
где ;
где 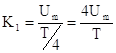 . .
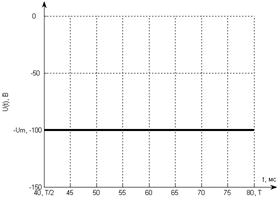
Рис 7.4 Третий типовой сигнал (ступень).
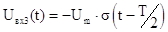 ; тогда ; тогда 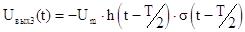 . .
Выходное напряжение будет
вычисляться по формуле:
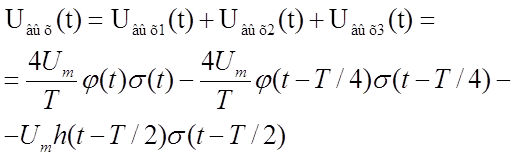
График выходного
напряжения показан на рис 7.7.
Сравнение результатов
разных методов анализа показан на рис 7.8.
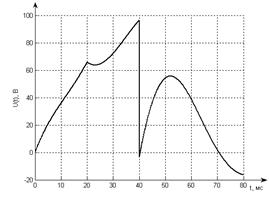
Рис 7.7 График напряжения на
выходе фильтра.
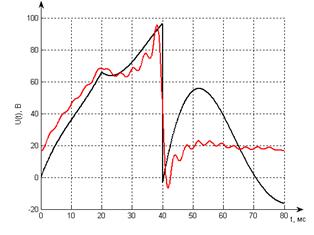
|
Решение, полученное при помощи переходной характеристики
и интеграла Дюамеля.
Решение, полученное при помощи комплексной передаточной
функции по напряжению и разложения входного сигнал в тригонометрический ряд
Фурье
|
|
  Рис 7.8 Сравнение
результатов разных методов анализа Рис 7.8 Сравнение
результатов разных методов анализа
8. Вывод
В
данной курсовой работе синтезирован полосовой фильтр типа “К” Г-обказный с
Т-образным входом.
Так
как это фильтр типа “К” , то ему свойственны все недостатки фильтров этого
типа
а)
Недостаточная крутизна АЧХ в районе граничных частот , что не обеспечивает избирательных
свойств фильтра.
б)
В зоне полосы прозрачности характеристические сопротивления являются
переменными , особенно это проявляется ближе к граничным частотам. По этому
согласование даже в зоне полосы прозрачности 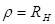 выполняется
на небольшом участке. выполняется
на небольшом участке.
Из
достоинств этого фильтра можно отметить простоту его реализации. Таким образом
синтез качественных фильтров представляет из себя трудоемкий процесс.
При
анализе фильтра была получена переходная характеристика цепи, из нее можно
определить быстродействие, колебательность цепи, время переходного процесса,
т.е. она отражает основные свойства системы и цепи.
9. Список
использованной литературы.
1 Атабеков Г. И. Линейные
электрические цепи: Учебник для вузов.-5-е изд., испр. и доп.— М.: Энергия,
1978.— 592 с. ил.
2.Атабеков Г. И.
Теоретические основы электротехники. —М.: Энергия, 1979. —592с.
3. Бессонов Л. А. Теоретические
основы электротехники. Электрические цепи. —М.: Высшая школа, 1978. —528с.
4. Шаров В. К., Широков Г.
И., Червяков В. И. Алгоритмическое и програмное обеспечение для расчета
электрических цепей с помощью ПЭВМ. —Калуга: КФ МГТУ им Н. Э. Баумана, 1997. —54с.
Приложение.
При
выполнение работы был использован математический пакет Matlab 7.0.
Листинг программы:
%T=80мс
w=78,5398
%график
h(t)
fplot(@h,[0 T])
grid on
box off
figure
%график Fi(t)
fplot(@fi,[0 T])
grid on
box off
figure
%ост графики
w=2*pi/0.08;
s=1;
T_=0;
T=0.080;
for t=0:0.0001:0.08
Uf(s)=A(1)/2;
Uv(s)=Uf(s)*Kjw(0);
Uout(s)=A(1)/2;
T_(s)=t*1000;
for i=1:20
Uf(s)=Uf(s)+A(i+1).*cos(i*w*t)+B(i).*sin(i*w*t);
Uv(s)=Uv(s)+A(i+1)*abs(Kjw(i*w))*cos(i*w*t+arg(Kjw(i*w)))+...
B(i)*abs(Kjw(i*w))*sin(i*w*t+arg(Kjw(i*w)));
gin(i,s)=A(i+1).*cos(i*w*t)+B(i).*sin(i*w*t);
gout(i,s)=A(i+1)*abs(Kjw(i*w))*cos(i*w*t+arg(Kjw(i*w)))+...
B(i)*abs(Kjw(i*w))*sin(i*w*t+arg(Kjw(i*w)));
end;
Uout(s)=(4*Um/T*fi(t)*g(t)-4*Um/T*fi(t-T/4)*g(t-T/4)-Um*h(t-T/2)*g(t-T/2));
s=s+1;
end
plot(T_,Uf)
grid on
box off;
figure
plot(T_,Uv)
grid on
box off;
figure
plot(T_,gin(1,:),'r',T_,gin(2,:),'b',T_,gin(3,:),'b',T_,gin(4,:),'g'...
,T_,gin(5,:),'b',T_,gin(6,:),'b',T_,gin(7,:),'b')
grid on
box off;
figure
plot(T_,gout(1,:),'r',T_,gout(2,:),'b',T_,gout(3,:),'b',T_,gout(4,:),'g'...
,T_,gout(5,:),'b',T_,gout(6,:),'b',T_,gout(7,:),'b')
grid on
box off;
figure
plot(T_,Uout)
grid on
box off;
figure
plot(T_,Uout,'b',T_,Uv,'r')
grid on
box off;
hold off;
%================================
function f=h(t)
f=1-0.7562057.*exp(-39.2962963.*t).*sin(103.93016939.*t);
%================================
function f=g(t)
if (t>=0) f=1;
else f=0;
end;
%----------------------%
function f=fi(t)
f=quad(@h,0,t);
%----------------------%
function f=arg(K)
f=atand(imag(K)/real(K));
%----------------------%
function f = Kjw(W)
p=j*W;
ff=((p^2)*0.0811+1000)/((p^2)*0.0811+p*6.3662+1000);
f=real(ff);
%----------------------%
|