Курсовая работа: Алгоритмы сортировки, поиска длиннейшего пути во взвешенном графе и поиска покрытия, близкого к кратчайшему
Курсовая работа: Алгоритмы сортировки, поиска длиннейшего пути во взвешенном графе и поиска покрытия, близкого к кратчайшему
Введение
Теория
алгоритмов и практика их построения и анализа является концептуальной основой
разнообразных процессов обработки информации. В настоящее время теория
алгоритмов образует теоретический фундамент вычислительных наук. Применение
теории алгоритмов осуществляется как в использовании самих результатов
(особенно это касается использования разработанных алгоритмов), так и в обнаружении
новых понятий и уточнении старых. С ее помощью проясняются такие понятия как
доказуемость, эффективность, разрешимость, перечислимость и другие.
Фактически,
алгоритм – это точно определенная (однозначная) последовательность простых
(элементарных) действий, обеспечивающих решение любой задачи из некоторого
класса, т.е. такой набор инструкций, который можно реализовать чисто
механически, вне зависимости от умственных способностей и возможностей
исполнителя.
Как заметил
Кнут: «Алгоритм должен быть определен настолько четко, чтобы его указаниям мог
следовать даже компьютер».
Эффективность
алгоритма определяется анализом, который должен дать четкое представление,
во-первых, о емкостной и, во-вторых, о временной сложности процесса.
Речь идет о
размерах памяти, в которой предстоит размещать все данные, участвующие в
вычислительном процессе (естественно, к ним относятся входные наборы,
промежуточная и выходная информация), а также физических ресурсах, затраченных
исполнителем.
В курсовой
работе представлены различные подходы и методы использования алгоритмов,
приведены оценки сложностей алгоритмов, реализации математических задач с
помощью алгоритмов. Проведена краткая характеристика используемых структур
данных, эффективность их применения в данной задаче
1. Выбор
варианта задания
В основе выбора индивидуального варианта задания лежит процедура
определения целочисленного остатка от деления выражения Y, образованного суммой
номера студента по журнальному списку и числом Х, полученным умножением
последней цифры номера группы на 100. После определения значения выражения Y находится остаток от
деления для соответствующего списка алгоритмов:
Y mod 4 + 1 – алгоритмы покрытия;
Y mod 6 + 1 – алгоритмы на графах;
Y mod 5 + 1 – алгоритмы сортировки.
Мой номер по
журнальному списку равен 5, группа АЕ-035. Поэтому имеем Y=5+5*100=505. Получаем
такие варианты:
А = 505 mod 4
+1 = 2;
B
= 505 mod 6 +1 = 2;
C
= 505 mod 5 +1 = 1.
Таким
образом, имеем следующие алгоритмы: покрытия – по методу «построение одного
кратчайшего покрытия», на графах – нахождение самого длинного пути, сортировки –
простыми включениями.
Постановка
задачи. Необходимо ввести таблицу покрытия. Алгоритм должен найти покрытие,
близкое к кратчайшему.
2.
Алгоритм сортировки
2.1
Математическое описание задачи и методов её решения
В общем
смысле сортировку следует понимать как процесс перегруппировки заданного
множества объектов в некотором определенном порядке. Её цель – облегчить
последующий поиск элементов в таком отсортированном множестве.
Если у нас
есть элементы а1, …, аn, то сортировка есть перестановка этих элементов
в массив ак1, …, акn, где при некоторой
упорядочивающей функции f выполняются отношения f(ak1)≤f(ak2)≤…≤f(akn).
Метод
сортировки называется устойчивым, если в её процессе относительное расположение
элементов с равными ключами не изменяется.
Существуют
такие алгоритмы сортировок массива: сортировка с помощью прямого включения,
прямого выбора, прямого обмена, включений с уменьшающимися расстояниями,
дерева, разделения и другие.
2.2
Словесное описание алгоритма и его работы
В силу
простоты алгоритм сортировки простыми включениями не требует разделения на
подпрограммы.
Элементы
мысленно делятся на уже «готовую» последовательность а1…а2
и исходную последовательность а1…аn. При каждом шаге, начиная
с i=2 и увеличивая i каждый раз на единицу,
из исходной последовательности извлекается i-й элемент и
перекладывается в готовую последовательность, при этом он вставляется в нужное
место.
Словесное
описание алгоритма сортировки простыми включениями:
0. В готовую
подпоследовательность записывается а1, во входную – а2,….аn.
1. i = 2.
2 Переносим элемент х = а
из входной подпоследовательности в готовую так, чтобы готовая
подпоследовательность осталась под сортированной. Для этого:
а) расширяем готовую
подпоследовательность слева: а0 = х – барьер;
б) просматривая элементы
готовой подпоследовательности слева направо, находим такой номер j что и ai <=x < ai+1;
в) если j=j-1, то переходим к пункту
г), иначе расширяем готовую
подпоследовательность справа, сдвигая ее элементы, начиная с ai вправо;
г) ai+1 = x
д) i = i + 1. Если i <=n, то переходим к п. 2,
иначе сортировка заканчивается.
Процесс может
закончиться при двух различных условиях: 1) найден элемент с ключом, меньшим,
чем ключ x;
2) достигнут конец готовой последовательности. Получается цикл с двумя
условиями. Поэтому для некоторого улучшения быстродействия применяется барьер –
a[0] присваивается
значение ключа x.
Проанализируем
этот алгоритм. Число сравнений (Сi) при i-м просеивании самое большее равно i-1, самое меньшее – 1;
если предположить, что все перестановки из n ключей равновероятны, то
среднее число сравнения – i/2. Число же пересылок (присваиваний элементов) Mi равно Сi+2 (включая барьер).
Поэтому общее число сравнений и число пересылок таковы:
Сmin=n-1, Mmin=3*(n-1)
Cave=(n2+n-2)/4, Mave=(n2+*n-10)/4,
Cmax=(n2+n-4)/4, Mmax=(n2+3n-4)/2.
Минимальные
оценки в случае уже упорядоченной исходной последовательности элементов,
наихудшие же оценки – когда они первоначально расположены в обратном порядке.
Очевидно, что приведенный алгоритм описывает метод устойчивой сортировки (см.
[1]).
Этот алгоритм
можно легко улучшить, поскольку готовая последовательность сама уже
упорядочена. Поэтому при поиске подходящей позиции для i-го ключа целесообразно
использовать двоичный поиск. При этом такой модифицированный алгоритм носит
название метода с двоичным включением.
Словесное описание
алгоритма сортировки с двоичным включением:
0. В готовую
подпоследовательность записывается а1, во входную а2,….аn.
1. i = 2
2 Переносим элемент
х=аi из входной подпоследовательности в готовую так, чтобы последняя
осталась под сортированной. Для этого:
а) организуем бинарный
поиск места включения х в готовую подпоследовательность: находим срединный
элемент готовой подпоследовательности – am, где m =] i/2 (, и сравниваем
его с х. Если am > х то ведем далее поиск в левой половине готовой
подпоследовательности, т.е. опять находим срединный элемент и сравниваем
его с х и т.д., пока не найдем номер j такой, что ai <=x < ai+1, иначе аналогично ведем
поиск в правой половине готовой подпоследовательности;
б) если j=j-1, то переходим к пункту
в), иначе расширяем готовую подпоследовательность справа, сдвигая ее элементы,
начиная с ai вправо;
в) ai+1 = х
3. i=i+1. Если i <= n, то переходим к п. 2,
иначе сортировка заканчивается.
Деление
пополам производится i*log2i. Число сравнений практически не зависит от начального
порядка элементов. В нижней части последовательности место включения
отыскивается несколько быстрее, чем в верхней, поэтому предпочтительна
ситуация, когда элементы немного упорядочены. Фактически, если элементы в
обратном порядке, потребуется минимальное число сравнений, если уже упорядочены
– максимальное:
C≈n*log2(log2-log2e±0,5).
Однако число
пересылок так и остается порядка n2. И на самом деле сортировка уже упорядоченного
массива потребует больше времени, чем метод с прямыми включениями (см. [1]).
2.3 Выбор
структур данных
Алгоритмы
сортировки очень сильно зависят от структуры данных, так что выделяют два
класса: сортировку массивов и сортировку последовательностей (файлов). В данной
работе рассматривается сортировка массивов. Тип данных «массив» удобен тем, что
хранится во внутренней памяти и имеет случайный доступ к элементам, то есть
более быстрый, чем у последовательности. Поэтому массивы целесообразно
использовать для хранения небольших, часто используемых множеств.
Обычно
упорядочивающая функция не вычисляется по какому-либо правилу, а хранится как
явная компонента (поле) каждого элемента. Её значение называется ключом элемента.
Поэтому для представления элемента хорошо подходит тип «запись», что на языке «Pascal» выглядит следующим
образом:
TYPE
item = RECORD key: INTEGER;
{здесь
описаны другие компоненты}
END;
Поскольку в
алгоритме сортировки используется только ключ элемента, то остальную информацию
об элементе можно опустить – считаем, что тип элемента определен как INTEGER. Можно выбрать и другой
тип, на котором определено общее отношение порядка.
Из выше
сказанного следует, что в процессе работы потребуются следующие переменные:
n – количество элементов
массива;
A – сортируемый массив;
i – переменная цикла (по
исходной последовательности);
j – переменная внутреннего
цикла (по готовой последовательности);
x – i-й ключ (переносимый
элемент).
Все
переменные целого типа.
2.4
Описание схемы алгоритма
Блок-схема
данного алгоритма изображена на рис. 2 в Приложении.
Алгоритм
работает следующим образом. Сначала вводятся исходные данные: длина массива и
его элементы (блоки 1, 2), затем организуется цикл по всей длине массива, во
время которого ставится «барьер» (блок 3) и проводится сравнение i-го ключа с элементами
готовой последовательности (стоящими раньше него). При этом все элементы,
большие этого ключа (это условие проверяется в блоке 4), сдвигаются вправо
(блок 5). Это происходит до тех пор, пока не встретится элемент меньший либо
равный данному ключу (по крайней мере барьеру). Тогда i-й ключ вставляется в эту
позицию (блок 6).
2.5 Контрольные примеры решения задачи с помощью алгоритма
сортировки простыми включениями
Пример сортировки массива, отсортированного случайным образом.
Пусть задан такой массив из восьми элементов:
(32,43,2,30,82,8,5,52) (см. Таб. 1).
| Начальные
ключи |
32 |
43 |
02 |
30 |
82 |
08 |
05 |
52 |
| i = 2 |
32 |
43 |
02 |
30 |
82 |
08 |
05 |
52 |
| i = 3 |
02 |
32 |
43 |
30 |
82 |
08 |
05 |
52 |
| i = 4 |
02 |
30 |
32 |
43 |
82 |
08 |
05 |
52 |
| i = 5 |
02 |
30 |
32 |
43 |
82 |
08 |
05 |
52 |
| i = 6 |
02 |
08 |
30 |
32 |
43 |
82 |
05 |
52 |
| i = 7 |
02 |
05 |
08 |
30 |
32 |
43 |
82 |
52 |
| i = 8 |
02 |
05 |
08 |
30 |
32 |
43 |
52 |
82 |
Пошаговое
решение:
Шаг 1:
1)
i=2;
2)
x=43; a[0]=43; j=1;
3)
x > a[j]=32;
3.2) a[2]= 43;
4)
i=3; i ≤ n=8 → п. 2;
Шаг 2:
2) x=2; a[0]=2;
j=2;
3)
x < a[j]=43;
3.1)
a[3]=43; j=1; → п. 3;
3)
x < a[j]=32;
3.1)
a[2]=32; j=0; → п. 3;
3)
x = a[j];
3.2)
a[1]=2;
4)
i=4; i<n → п. 2;
Шаг 3:
2)
x=30; a[0]=30; j=3;
3)
x < a[j]=43;
3.1)
a[4]=43; j=2; → п. 3;
3)
x < a[j]=32;
3.1)
a[3]=32; j=1; → п. 3;
3)
x > a[1]=2
3.2)
a[2]=30;
4)
i=5; i<n → п. 2;
Шаг 4:
2)
x=82; a[0]=82; j=4;
3)
x > a[j];
3.2)
a[5] = 82;
4)
i=6; i<n → п. 2;
Шаг 5:
2)
x=8; a[0]=8; j=5;
3)
x < a[j]=82;
3.1)
a[6]=82; j=4; → п. 3;
3)
x < a[j]=43;
3.1)
a[5]=43; j=3; → п. 3;
3)
x < a[j]=32;
3.1)
a[4]=32; j=2; → п. 3;
3)
x < a[j]=30;
3.1)
a[3]=30; j=1; → п. 3;
3)
x > a[j]=2;
3.2)
a[2]=8;
4)
i=7; i<n → п. 2;
Шаг 6:
2)
x=5; a[0]=5; j=6;
3)
x < a[j]=82;
3.1)
a[7]=82; j=5; → п. 3;
3)
x < a[j];
3.1)
a[6]=43; j=4; → п. 3;
3)
x < a[j]=32;
3.1)
a[5]=32; j=3; → п. 3;
3)
x < a[j]=30;
3.1)
a[4]=30; j=2; → п. 3;
3)
x < a[j]=8;
3.1)
a[3]=8; j=1; → п. 3;
3)
x > a[j]=2;
3.2)
a[2]=5;
4)
i=8; i≤n → п. 2;
Шаг 7:
2)
x=52; a[0]=52; j=7;
3)
x < a[j]=82;
3.1)
a[8]=82; j=6; → п. 3;
3)
x > a[j]=43;
3.2)
a[7]=52;
4) i=9; i>n → конец алгоритма.
Таким
образом, имеем 21 пересылку элементов и 20 сравнений.
Пример
сортировки уже отсортированного массива.
Пусть задан такой массив из восьми элементов:
(2,5,8,30,32,43,52,82).
Пошаговое
решение:
Шаг 1:
1) i=2;
2) x=5; a[0]=2; j=1;
3)
x > a[j]=2;
3.2)
a[2]=5;
4)
i=3; i<n → п. 3;
Шаг 2:
2)
x=8; a[0]=8; j=2;
3)
x > a[j]=5;
3.2)
a[3]=8;
4)
i=4; i<n → п. 3;
Шаг 3:
2)
x=30; a[0]=30; j=3;
3)
x > a[j]=8;
3.2)
a[4]=30;
4)
i=5; i<n → п. 3;
Шаг 4:
2)
x=32; a[0]=32; j=4;
3)
x > a[j]=30;
3.2)
a[5]=32;
4)
i=6; i<n → п. 3;
Шаг 5:
2)
x=43; a[0]=43; j=5;
3)
x > a[j]=32;
3.2)
a[6]=43;
4)
i=7; i<n → п. 3;
Шаг 6:
2)
x=52; a[0]=52; j=6;
3)
x > a[j]=43;
3.2)
a[7]=52;
4)
i=8; i≤n → п. 3;
Шаг 7
2)
x=82; a[0]=82; j=7;
3)
x > a[j]=52;
3.2)
a[8]=82;
4)
i=9; i>n →конец алгоритма.
Таким образом
получили 7 пересылок и 7 сравнений.
Пример
сортировки массива, отсортированного в обратном порядке.
Пусть задан такой массив из восьми элементов:
(82,52,43,32,30,8,5,2).
Пошаговое
решение:
Шаг 1:
1) i=2;
2) x=52; a[0]=52; j=1;
3)
x< a[j]=52;
3.1)
a[2]=82; j=0; → п. 3;
3)
x=a[j];
3.2)
a[1]=52;
4)
i=3; i<n → п. 2;
Шаг 2:
2)
x=43; a[0]=43; j=2;
3)
x < a[j]=82;
3.1)
a[3]=82; j=1; → п. 3;
3)
x < a[j]=52;
3.1)
a[2]=52; j=0; → п. 3;
3)
x = a[j];
3.2)
a[1]=43;
4)
i=4; i<n → п. 2;
Шаг 3:
2)
x=32; a[0]=32; j=3;
3)
x < a[j]=82;
3.1)
a[4]=82; j=2; → п. 3;
3)
x < a[j]=52;
3.1)
a[3]=52; j=1; → п. 3;
3)
x < a[j]=43;
3.1)
a[2]=43; j=0; → п. 3;
3)
x=a[j];
3.2)
a[1]=32;
4)
i=5; i<n → п. 2;
Шаг 4:
2)
x=30; a[0]=30; j=4;
3)
x < a[j]=82;
3.1)
a[5]=82; j=3; → п. 3;
3)
x < a[j]=52;
3.1)
a[4]=52; j=2; → п. 3;
3)
x < a[j]=43;
3.1)
a[3]=43; j=1; → п. 3;
3)
x < a[j]=32;
3.1)
a[2]=32; j=0; → п. 3;
3)
x=a[j];
3.2)
a[1]=30;
4)
i=6; i<n → п. 2;
Шаг 5:
2)
x=8; a[0]=8; j=5;
3)
x < a[j]=82;
3.1)
a[6]=82; j=4; → п. 3;
3)
x < a[j]=52;
3.1)
a[5]=52; j=3; → п. 3;
3)
x < a[j]=43;
3.1)
a[4]=43; j=2; → п. 3;
3)
x < a[j]=32;
3.1)
a[3]=32; j=1; → п. 3;
3)
x < a[j]=30;
3.1)
a[2]=30; j=0; → п. 3;
3)
x=a[j];
3.2)
a[1]=8;
4)
i=7; i<n → п. 2;
Шаг 6:
2)
x=5; a[0]=5; j=6;
3)
x < a[j]=82;
3.1)
a[7]=82; j=5; → п. 3;
3)
x < a[j]=52;
3.1)
a[6]=52; j=4; → п. 3;
3)
x < a[j]=43;
3.1)
a[5]=43; j=3; → п. 3;
3)
x < a[j]=32;
3.1)
a[4]=32; j=2; → п. 3;
3)
x < a[j]=30;
3.1)
a[3]=30; j=1; → п. 3;
3)
x < a[j]=8;
3.1)
a[2]=8; j=0; → п. 3;
3)
x=a[j];
3.2)
a[1]=5;
4)
i=8; i<n → п. 2;
Шаг 7:
2)
x=2; a[0]=2; j=7;
3)
x < a[j]=82;
3.1)
a[8]=82; j=6; → п. 3;
3)
x < a[j]=52;
3.1)
a[7]=52; j=5; → п. 3;
3)
x < a[j]=43;
3.1)
a[6]=43; j=4; → п. 3;
3)
x < a[j]=32;
3.1)
a[5]=32; j=3; → п. 3;
3)
x < a[j]=30;
3.1)
a[4]=30; j=2; → п. 3;
3)
x < a[j]=8;
3.1)
a[3]=8; j=1; → п. 3;
3)
x < a[j]=5;
3.1)
a[2]=5; j=0; → п. 3;
3)
x=a[j];
3.2)
a[1]=2;
4)
i=9; i>n → конец алгоритма.
Таким
образом, имеем 35 сравнений и 35 пересылок.
3. Алгоритм
покрытия по методу «Построение одного кратчайшего покрытия»
3.1
Математическое описание задачи и методов её решения
Пусть 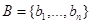 -опорное множество. Имеется
множество -опорное множество. Имеется
множество
подмножеств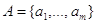 множества B ( множества B (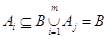 ). Каждому подмножеству ). Каждому подмножеству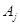 сопоставлено число сопоставлено число 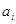 , называемой ценой.
Множество , называемой ценой.
Множество 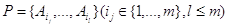 называется решением задачи
о покрытии, или просто покрытием, если выполняется условие называется решением задачи
о покрытии, или просто покрытием, если выполняется условие 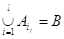 , при этом цена , при этом цена 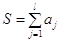 . Термин «покрытие»
означает, что совокупность множеств . Термин «покрытие»
означает, что совокупность множеств 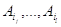 содержит
все элементы множества В, т.е. «покрывает» множество B содержит
все элементы множества В, т.е. «покрывает» множество B
Безизбыточным
называется покрытие, если при удалении из него хотя бы одного элемента оно
перестает быть покрытием. Иначе – покрытие избыточно.
Покрытие Р
называется минимальным, если его цене 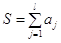 -
наименьшая среди всех покрытий данной задачи. -
наименьшая среди всех покрытий данной задачи.
Покрытие Р
называется кратчайшим, если l – наименьшее среди всех покрытий данной задачи.
Удобным и наглядным
представлением исходных данных и их преобразований в задаче о покрытии является
таблица покрытий. Таблица покрытий – это матрица Т отношения принадлежности
элементов множеств 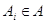 опорному
множеству В. Столбцы матрицы сопоставлены элементам множества В, строки – элементам
множества опорному
множеству В. Столбцы матрицы сопоставлены элементам множества В, строки – элементам
множества
А: 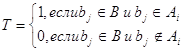
Нули в матрице T не проставляются.
Имеются следующие
варианты формулировки задачи о покрытии:
1. Требуется найти все
покрытия. Для решения задачи необходимо выполнить полный перебор всех
подмножеств множества А.
2. Требуется найти только
безубыточные покрытия. Не существует простого и эффективного алгоритма, не
требующего построения всех избыточных покрытий: хорошо, если уменьшается их
количество. (Используется граничный перебор либо разложение по столбцу в ТП).
Требуется найти одно
безизбыточное покрытие. Решение задачи основано на сокращении таблицы.
Задачи о покрытии могут
быть решены точно (при небольшой размерности) либо приближенно (см. [2]).
Для нахождения точного
решения используются такие алгоритмы.
1) Алгоритм полного
перебора. (Основан на методе упорядочения перебора подмножеств множества А).
2) Алгоритм граничного
перебора по вогнутому множеству. (Основан на одноименном методе сокращения
перебора).
3) Алгоритм разложения по
столбцу таблицы покрытия. Основан на методе сокращения перебора, который
состоит в рассмотрении только тех строк таблицы покрытия, в которых имеется «1»
в выбранном для разложения столбце.
4) Алгоритм сокращения
таблицы покрытия. Основан на методе построения циклического остатка таблицы
покрытия, для которого далее покрытие строится методами граничного перебора
либо разложения по столбцу.
Приближенное решение
задачи о покрытии основано на следующем соображении. Если даже сокращенный
перебор приводит к очень трудоемкому процессу решения, то для получения ответа
приходится отказываться от гарантий построения оптимального решения
(минимального либо кратчайшего); однако целесообразно получить не самый худший
результат – хотя бы безызбыточное покрытие, удовлетворяющее необходимому
условию. При этом в ущерб качеству можно значительно упростить процесс решения.
Для случая построения
одного кратчайшего покрытия используется алгоритм построения циклического
остатка таблицы покрытий и множества ядерных строк.
3.2 Словесное описание
алгоритма и его работы
0) Считаем исходную
таблицу покрытий текущей, а множество ядерных строк – пустым.
1) Находим ядерные
строки, запоминаем множество ядерных строк. Текущую таблицу покрытий сокращаем,
вычеркивая ядерные строки и все столбцы, покрытые ими.
2) Вычеркиваем
антиядерные строки.
3) Вычеркиваем
поглощающие столбцы.
4) Вычеркиваем
поглощаемые строки.
5) Если в результате
выполнения пунктов с 1 по 4 текущая таблица покрытий изменилась, снова
выполняем пункт 1, иначе преобразование заканчиваем.
Поэтому алгоритм работы
следующий:
1) ввод числа строк и
столбцов таблицы покрытия;
2) ввод таблицы покрытия;
3) поиск ядерных строк.
Если их нет, то п. 4. Иначе, запоминаем эти ядерные строки. Ищем столбцы,
покрытые ядерными строками. Вычеркиваем все ядерные строки и столбцы, покрытые
ими.
4) вычеркивание
антиядерных строк. Переход в п. 5.
6) вычеркивание
поглощающих столбцов.
7) вычеркивание
поглощаемых строк.
8) если в результате
преобразований таблица покрытий изменилась, выполняем пункт 3. Иначе – вывод
множества покрытия, конец алгоритма.
3.3 Выбор структур данных
Из анализа задачи и ее данных видно, что алгоритм должен работать
с таблицей покрытия и с некоторыми переменными, которые представлены ниже (все
переменные целого типа):
m – количество строк таблицы покрытия;
n – количество столбцов таблицы покрытия;
i, j – переменные цикла по строкам и столбцам соответственно;
Sprev – предыдущая сумма столбца либо строки;
Scurr – текущая сумма столбца либо строки.
Таблица покрытия – это двумерная матрица. Ее целесообразно
представить в виде двумерного массива A (m, n).
P – одномерный массив для хранения номеров строк, покрывающих
матрицу. Для хранения номеров выбран массив, поскольку количество строк, хотя и
неизвестно заранее, ограничено количеством строк матрицы покрытия (m).
3.4 Описание схемы алгоритма
Блок-схема данного алгоритма изображена на рис. 3 в
Приложении.
Сначала вводятся исходные данные: размерность таблицы m и n и сама таблица покрытия
(блок 1). Далее происходит поиск пустого столбца (блок 2): это целесообразно,
поскольку, если хотя бы один столбец не покрыт, то и не существует покрытия
данной таблицы, и, следовательно, конец алгоритма. Далее, если не найдено
пустого столбца (проверка в блоке 3), – поиск ядерных строк (блок 4), после – столбцов,
покрытых ими (блок 5). После этого вычеркиваются все столбцы и строки,
найденные в блоках 4,5 (блок 6).Вычеркиваются антиядерные строки (блок 7).
Вычеркиваются поглощающие столбцы (блок 8). Вычеркиваются поглощаемые строки
(блок 9). Если в результате выполнения блоков 6–9 текущая таблица покрытий
изменилась, то выполняется блок 4; иначе следует вывод найденного кратчайшего
покрытия в виде номеров строк, покрывающих таблицу. Затем конец алгоритма.
3.5 Подпрограммы основного алгоритма
Функция MOJNO_LI(A) ведет поиск пустых столбцов, то есть не покрываемых ни
одной строкой. Блок-схема этой функции представлена на рис. 3.1
Приложения. Организуется цикл по всем столбцам (блоки 1–6). В каждом столбце
идет счет нулей (счетчик i инициализируется в каждом проходе – блок 2; счет ведется в
блоке 5), то есть если встречается хотя бы одна единица (проверка в блоке 3),
то происходит переход в следующий столбец. Алгоритм работает до тех пор, пока
не будет достигнут конец таблицы (то есть конец цикла по j, блок6) либо пока не
будет сосчитано m нулей в одном столбце (проверка условия в блоке 4), то есть i=m. Функция возвращает 0,
если найдено m
нулей, и 1, если достигнут конец таблицы.
Функция YAD-STROKA(A) ведет поиск ядерных строк. В блоке 1 S инициализируется
значением 0. Далее организуется цикл по всем столбцам (блок 2). Обнуляем
текущую сумму (блок 4) и считаем сумму в j-м столбце (цикл в блоках
5–7 и собственно суммирование элементов в блоке 6). Далее сравниваем полученную
сумму S
с 1 (блок 8). Если текущая сумма равна 1, запоминаем её и номеру этого столбца присваиваем
0 (блок 9), иначе переходим к следующему столбцу. Таким образом, по окончании
цикла по j
в переменной yad stroka(A)
будет храниться массив ядерных строк. Блок-схема данного алгоритма изображена
на рис. 3.2 в Приложении.
Функция ANTI_STROK(A) ведет поиск антиядерных
строк. Переменной S2 присваивается значение 0. Организовывается цикл по строкам.
Ищется сумма каждой строки и если она равна 0, то строка вычеркивается. Если нет,
то переходим к следующей строке. Блок-схема данного алгоритма изображена на
рис. 3.3 в Приложении.
Процедура VICHEK(A) реализует вычеркивание
столбцов, покрытых ядерными строками. Аналогично данная процедура работает и
для самих ядерных строк, и для антиядерных строк, поглощающих столбцов,
поглощаемых строк. Чтобы данный столбец (строку) «вычеркнуть», необходимо поставить
1 на его (ее) пересечении с нулевой строкой (столбцом). Блок-схема данного
алгоритма изображена на рис. 3.4 в Приложении.
Процедура VIVOD(P) реализует вывод
полученного множества строк из массива P. Для этого организуется
цикл по элементам массива Р (блоки 1–4), в котором проверяется отмечен ли номер
строки i
единицей (блок 2). Если да, то выводится номер строки i (блок 3). Блок-схема данного
алгоритма изображена на рис. 3.5 в Приложении.
3.6 Пример
работы алгоритма
Пусть задана
таблица покрытий (см. Таб. 3). Рассмотрим пример работы алгоритма.
1. Множество
ядерных строк пустое.
| B |
B1 |
B2 |
B3 |
B4 |
B5 |
B6 |
| А1 |
1 |
|
1 |
|
|
1 |
| А2 |
1 |
|
|
1 |
1 |
|
| A3 |
1 |
|
|
1 |
1 |
|
| А4 |
|
1 |
1 |
|
|
1 |
2. Множество
антиядерных строк пустое.
3.
Вычеркиваем столбцы В1, В3, В5, В6 как поглощающие
4.
Вычеркиваем строку А2 как поглощенную.
Теперь
таблица покрытий будет иметь вид (см. Таб. 4)
Таб. 4.
1.
Множество
ядерных строк Р={A3, A4}.
2.
Множество
антиядерных строк А={А1}.
3.
Множество
поглощающих столбцов пустое.
4.
Множество
поглощаемых строк пустое.
Теперь таблица покрытий
примет вид (см. Таб 5)
Таб. 5.
Таким образом кратчайшее
покрытие {A3,
A4}.
4. Алгоритм нахождения
длиннейшего пути в графе
4.1 Математическое описание
задачи и методов её решения
Графом (G, X) называется
совокупность двух конечных множеств: множества точек, которые называются
вершинами (X = {Х1,…, Хn}), и множества связей в
парах вершин, которые называются дугами, или ребрами ((Хi, Хj) Î G) в зависимости от
наличия или отсутствия направленности связи.
Ребром называются две
встречные дуги (Хi, Хj) и (Хj, Хi). На графе они изображаются одной
линией без стрелки. Ребро, или дуга, концевые вершины которого совпадают,
называется петлей.
Если на каждом ребре
задается направление, то граф (G, Х) называется ориентированным. В противном случае граф
называется неориентированным.
Две вершины, являющиеся
концевыми для некоторого ребра или некоторой дуги, называются смежными.
Соответственно этот граф может быть представлен матрицей смежности либо
матрицей инцидентности.
Матрицей инцидентности
называется прямоугольная матрица с числом строк, равным числу вершин графа, и с
числом столбцов, равным количеству ребер (дуг) графа. Элементы матрицы а задаются
следующим образом: «1» ставится в случае если вершина vi, инцидентна ребру uj; «0» – в противном
случае.
Вершина и ребро (дуга)
называются инцидентными друг другу, если вершина является для этого ребра
(дуги) концевой точкой.
Путь из начальной вершины
хн к кончиной вершине хк – последовательность дуг,
начинающаяся в вершине хн Î Х, заканчивающаяся в
вершине хк Î Х, и такая, что конец очередной дуги является началом следующей:
(хн, хi1) (хi1, хi2) (хi2… хik) (хik, xk) = (xн, хк).
Элементарный путь – путь,
в котором вершины не повторяются.
Простой путь – путь, в
котором дуги не повторяются.
Маршрут – последовательность
ребер, составляющих, как и путь, цепочку.
Длина пути взвешенного
графа определяется как сумма весов – его дуг. Если граф не взвешен, то можно
считать веса дуг равными 1.
Кратчайшим путем между
выделенной парой вершин хн и хк называется путь, имеющий
наименьшую длину среди всех возможных путей между этими вершинами.
При построении
длиннейшего пути рассматриваются элементарные или простые длиннейшие пути,
длиннейшие пути с заданным числом выполненных циклов. Длиннейший путь между хн
и хк – путь, имеющий наибольшую длину среди всех возможных путей
между этими вершинами.
Таким образом, нахождение
длиннейшего пути – это поиск множества вершин, составляющих этот путь.
Волновой алгоритм получил
свое название из-за того, что сам принцип его функционирования основан на «испускании
волны,» какого-либо гипотетического возмущения по результатам которого имеется
возможность судить о количестве смежных с выделенной вершин, а так же о
расстоянии (длине дуги) до каждой из них.
Очевидно, что к каждой
вершине могут идти от вершины X н несколько путей, суммы длин дуг по
разным путям различны. При поиске длиннейшего пути следует выбирать
максимальную сумму. Волны распространения веса по разным путям доходят до
каждой вершины последовательно, при очередной волне необходимо оставить либо
старый вес вершины, либо заменить его на новый (больший). Поэтому при расчете
веса вершины X i за счет волны, подошедшей к ней по дуге (X j,
X i), производится вычисление веса V i по формуле V i
=max (V i, V j + l ji).
Веса вершин в процессе распространения
волны могут меняться неоднократно. При каждом изменении веса V i
вершины это увеличение веса необходимо передать вершинам исхода X i,
т.е. необходимы специальные средства, отражающие факты получения вершиной
нового веса и передачу его другим вершинам. В качестве такого средства
используется массив номеров вершин, получивших новый вес (при каждом изменении
веса номер вершины включается в этот массив, если его там не было, при передачи
веса исключается).
4.2 Словесное описание
алгоритма и его работы
1. Все вершины графа
получают веса V i =0, номер вершины X н
заносится в массив М номеров вершин, изменивших вес. Остальные вершины X i
не попадают в массив М.
2. Если массив М пуст,
выполняется п. 3, иначе выбирается с исключением из его очередная вершина
X i и пересчитываются веса вершин, принадлежащих исходу G (X i)
вершины X i:
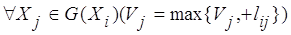
Если вес V j изменяется,
то номер j включается с приведением подобных в М. Снова выполняется п. 2.
3. Если вес 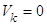 , то делается вывод, что
пути из вершины X н к вершине X k не существует, иначе
выполняется процедура выделения дуг, двигаясь в обратном порядке проверяем
выполняется ли условие X i – X j = l ij, для
входов , то делается вывод, что
пути из вершины X н к вершине X k не существует, иначе
выполняется процедура выделения дуг, двигаясь в обратном порядке проверяем
выполняется ли условие X i – X j = l ij, для
входов 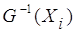 вершины X i,
если оно выполняется, то вершина X j и дуга l ij выделяются. вершины X i,
если оно выполняется, то вершина X j и дуга l ij выделяются.
4. После выделения дуг
строятся длиннейшие пути, длины которых равны V k.
При построении длиннейших
путей рассматриваются элементарные или простые длиннейшие пути,
длиннейшие пути с заданным числом выполнения циклов.
4.3 Структуры данных
Из самой структуры
алгоритма очевидно, что для его функционирования необходимы:
1. Массив В-массив
дуг-связностей в ячейках с номерами i, j которого будет находиться вес соответствующей дуги l ij.
2.
Массив
М – массив изменивших свой вес вершин.
3.
Массив
Е – массив содержащий значения весов и состояний вершин.
4.
Массив
Р – массив содержащий выделенные дуги.
5.
Ряд
индексных переменных необходимых для перемещения по массивам В, Е, Р, а также
содержащие индекс текущей вершины, и ряд буферных переменных необходимых для
текущих арифметических и циклических операций (все индексы должны быть
целочисленного типа).
4.4 Контрольный пример
Для подробного описания
действия волнового алгоритма поиска длиннейшего пути воспользуемся графом
задаваемым таблице связностей:
|
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
| X1 |
|
1 |
4 |
|
|
|
| X2 |
|
|
2 |
5 |
|
|
| X3 |
|
|
|
2 |
4 |
|
| X4 |
|
|
|
|
1 |
4 |
| X5 |
|
|
|
|
|
2 |
| X6 |
|
|
|
|
|
|
Таким образом, зная
таблицу связностей можно построить граф для более наглядной иллюстрации
примера:
Итак, на первом проходе волнового
алгоритма выполняется пункт 1, т.е. устанавливаются значения весов всех вершин
в нуль, и помещает в массив М индекс начальной вершины, математически это можно
записать так:
Шаг №1:
П. 1: 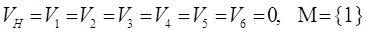
На втором проходе, т. к.
М<>0, выполняется пункт 2, из массива М забирается первый элемент, этот
индекс присваивается индексной переменной i составляется множество исходов для
вершины Х i, а затем вычисляются веса смежных вершин:
Шаг №2:
П. 2: 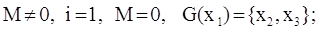
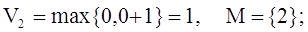
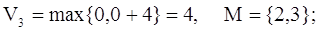
Как видно из приведенных
записей, в результате этого прохода две вершины: вторая и третья получили новые
веса, и соответственно в массив М попали их индексы, так как до этого они в нем
не содержались. (В дальнейшем для краткости изложения будут приводиться
преимущественно математические записи работы алгоритма).
Шаг №3:
П. 2: 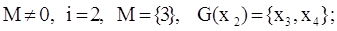
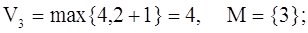
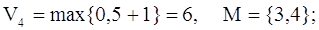
Следует отметить, что в
результате этого прохода вершина Х 3 не поменяла своего веса, так
как уже имела максимально возможный.
Шаг №4:
П. 2: 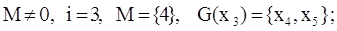
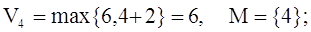
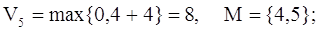
Шаг №5:
П. 2: 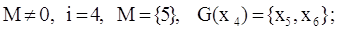
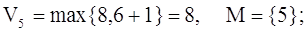
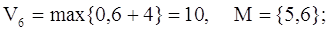
Шаг №6:
П. 2: 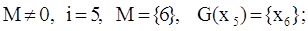
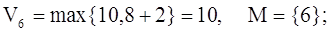
Шаг №7:
П. 2: 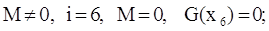
Шаг №8:
П. 2: М=0,
выполняется п. 3.
Итак, на данный момент
получен граф, все вершины которого приобрели максимально возможные значения. А
так как массив изменивших вес вершин пуст, то управление передается третьему
пункту алгоритма, который отмечает длиннейший путь. Следует особо отметить, что,
как видно из предыдущих вычислений, максимальные веса вершин могут быть
достигнуты при продвижению по разным дугам. Для большей наглядности примера
ниже приведен вид графа на данном этапе:
На этапе выполнения
третьего пункта алгоритма критерием для выделения дуги, как и для алгоритма
нахождения кратчайшего пути, является совпадение разности весов соответствующих
вершин с весом самой дуги. Таким образом, начиная с вершины Х6 получим:
Шаг №9: Для выделенной
вершины 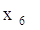
П. 3: 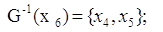
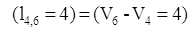 , поэтому дуга , поэтому дуга 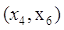 выделяется. выделяется.
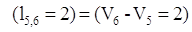 , и дуга , и дуга 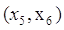 выделяется, одновременно выделяются
вершины выделяется, одновременно выделяются
вершины 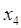 и и 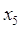 . .
Шаг №10: Для выделенной
вершины 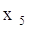
П. 3: 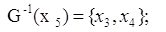
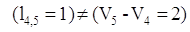 , поэтому дуга , поэтому дуга 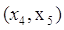 не выделяется. не выделяется.
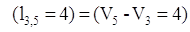 , и дуга , и дуга 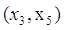 выделяется, одновременно выделяется, одновременно
выделяется вершина 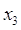 . .
Шаг №11: Для выделенной
вершины 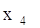
П. 3: 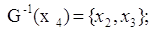
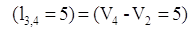 , поэтому дуга , поэтому дуга 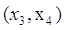 выделяется. выделяется.
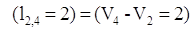 , и дуга , и дуга 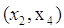 выделяется, одновременно выделяется
вершина выделяется, одновременно выделяется
вершина 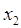 , следует отметить, что
вершина , следует отметить, что
вершина 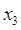 не выделяется, так как уже
выделена. не выделяется, так как уже
выделена.
Шаг №12: Для выделенной
вершины 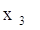
П. 3: 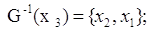
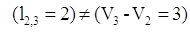 , поэтому дуга , поэтому дуга 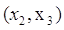 не выделяется. не выделяется.
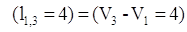 , и дуга , и дуга 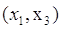 выделяется, одновременно выделяется
вершина выделяется, одновременно выделяется
вершина 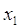 . .
Шаг №13: Для выделенной
вершины 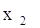
П. 3: 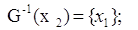
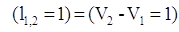 , и дуга , и дуга 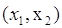 выделяется, следует отметить,
что вершина выделяется, следует отметить,
что вершина 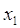 не выделяется, так как уже
выделена. не выделяется, так как уже
выделена.
Шаг №14: Для выделенной
вершины 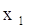
П. 3: 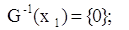
Так как в данную вершину
не входит не оной дуги и больше нет отмеченных вершин, переходим к этапу
составления длиннейшего пути.
Итак соединяя дуги по принципу:
конечный индекс предыдущей – начальный последующий, получаем три длиннейших
путей 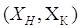 длиной 10: длиной 10:
1.
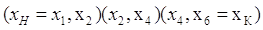
2.
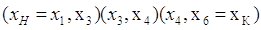
3.
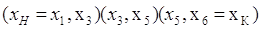
Для большей наглядности
изобразим граф в своем конечном состоянии, нанеся на него значения весов
вершин, веса дуг, а так же выделив длиннейшие пути и вычисление длин дуг этих
путей:
Приведем табличный метод
записи процесса:
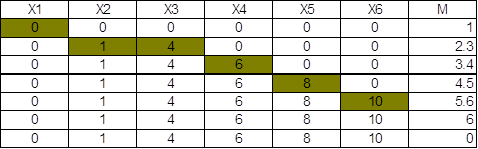
Заключение
В данной
работе разработаны алгоритмы сортировки, поиска длиннейшего пути во взвешенном графе
и поиска покрытия, близкого к кратчайшему. Алгоритмы исполнены с нужной
степенью детализации, необходимой для понимания их работы. Рассмотрены пути
улучшения эффективности каждого алгоритма учитывая требования конкретной
задачи.
Большое
внимание уделено сравнению возможного использования нескольких структур данных,
проведён анализ эффективности работы алгоритма в зависимости от используемой
структуры.
Рассмотрена
сложность каждого алгоритма, её зависимость от условий данной задачи, методы
упрощения и облегчения понимания алгоритма.
|