Курсовая работа: Абстрактный синтез конечного автомата
Курсовая работа: Абстрактный синтез конечного автомата
СОДЕРЖАНИЕ
Введение
1.
Абстрактный синтез конечного автомата
1.1
Формирование алфавитного оператора
1.2
Приведение оператора к автоматному виду
1.3
Построение графа переходов абстрактного автомата
1.4
Минимизация абстрактного автомата
2. Структурный
синтез конечного автомата
2.1
Кодирование состояний, входных и выходных сигналов
2.2
Формирование функций возбуждения и выходных сигналов структурного автомата
Заключение
Список
литературы
ВВЕДЕНИЕ
Теория автоматов – это
теория, на которой основаны экспериментальные методы исследования в
кибернетике. При подходе к теории автоматов, как к части теории алгоритмов,
центральной проблемой является изучение возможностей автоматов в терминах
множеств слов, с которыми работают автоматы.
Можно выделить два
основных аспекта работы автомата.
1.
Автоматы-распознаватели,
которые распознают входные слова, т.е. отвечают на вопрос, принадлежит ли
поданное на вход слово данному множеству.
2.
Автоматы-преобразователи,
которые преобразуют входные слова в выходные, т.е. реализуют автоматные
отображения.
Одной из задач теории
автоматов является задача описания автомата и его реализации, т.е.
представления автомата как структуры, состоящей из объектов фиксированной
сложности. В этом отношении теория автоматов оказалось наиболее развитой ветвью
теории алгоритмов.
Общая теория автоматов
подразделяется на абстрактную теорию и структурную теорию автоматов.
Абстрактная теория автоматов занимает промежуточное положение между алгеброй и
логикой. С точки зрения приложений значение абстрактной теории автоматов отнюдь
не сводится к удовлетворению запросов одной лишь вычислительной техники.
Современная теория автоматов представляет собой математический аппарат для
решения широкого класса комбинаторных проблем.
Структурная теория
автоматов позволяет реализовать абстрактный автомат на элементах, принадлежащих
к заранее заданному классу.
Для
преобразования дискретной информации в различных областях техники используются
цифровые автоматы. К цифровым автоматам относятся отдельные узлы и блоки
специализированных и универсальных ЦВМ и ЦВМ в целом. Цифровыми автоматами
могут быть названы также устройства, в автоматике, телемеханике, радиолокации и
других областях техники, в которых требуется выполнять преобразование над
сигналами, представленные в дискретной (цифровой) форме.
Первое
правило функционирования автоматов заключается в следующем. Автомат
необязательно должен запоминать входные истории. Вполне достаточно, чтобы
автомат запомнил класс эквивалентностей, к которому приходится данная история.
Второе
правило функционирования автоматов состоит в том, что на один и тот же входной
сигнал конечный автомат может реагировать по-разному, в зависимости от того, в
каком состоянии он находится в настоящий момент.
Конечный
автомат - это устройство, работающее в дискретные моменты времени, или такты.
На вход конечного автомата в каждом такте поступает один из возможных
входных сигналов, а на его выходе появляется выходной сигнал, являющийся
функцией его текущего состояния и поступившего входного сигнала.
Внутренние
состояния автомата также меняются. Моменты срабатывания (такты), определяются
либо принудительно тактирующими синхросигналами, либо асинхронно, наступлением
внешнего события, то есть приходом сигнала.
Существует
два вида реализации конечного автомата - аппаратная и программная. В первую
очередь, реализация конечного автомата требует построения устройства памяти для
запоминания текущего состояния автомата. Обычно используются двоичные элементы
памяти, или триггеры, запоминающие значение одного двоичного разряда.
1.
АБСТРАКТНЫЙ СИНТЕЗ КОНЕЧНОГО АВТОМАТА
1.1
Формирование алфавитного оператора
Для определения
параметров задания необходимо ввести первичную информацию:
- порядковый номер в
журнале;
- год поступления;
- номер группы;
Для данного задания это
соответственно:
21,
08, 02.
Из этих цифр необходимо
составить правильную десятичную дробь, в которой эти цифры следуют сразу после
запятой:
Y1=
0,210802
Вторичная информация Y,Y3
,Y4
получаются путем возведения 1
в степени 2, 3, 4 и удалением в дроби всех нулей между запятой и первой
значимой цифрой.
Y2
= 0,444374
Y3
= 0,93675
Y4
= 0,19747
Для получения значений входных
и выходных сигналов автомата необходимо полученные десятичные дроби
преобразовать в двоичный код до шестнадцатого знака.
В результате
преобразований получены следующие значения заданных сигналов.
Y1
= 0011010111110111
Y2
= 0111000111000010
Y3 =
1110111111001110
Y4
= 0011001010001101
Полученные значения
записываются в столбцах: первые 8 значений в левой части, вторые 8 – в правой
части. Алфавитный оператор соответствия представлен в таблице 1.
Таблица 1. Алфавитный
оператор соответствия
| Входные сигналы |
Выходные сигналы |
| 0010 |
1111 |
| 0110 |
1110 |
| 1111 |
1000 |
| 1101 |
1000 |
| 0010 |
0011 |
| 1010 |
1011 |
| 0011 |
1110 |
| 1110 |
1001 |
1.2 Приведение оператора к автоматному виду
Для того чтобы оператор
преобразовался к автоматному виду, необходимо выполнение трех условий:
1. Любым двум
одинаковым начальным отрезкам входных слов должны соответствовать одинаковые
начальные отрезки выходных слов;
2. Длина входного слова
должна равняться длине выходного слова;
3. Последний символ
должен возвращать автомат в начальное состояние.
Данный оператор уже
выровнен, так как длина каждого из входных слов равна длине соответствующего
выходного слова. Каждому входному слову здесь сопоставляются не более одного
выходного слова, поэтому оператор однозначен. Однако он не удовлетворяет
условию полноты.
Таким образом,
автоматный вид оператора примет, следующий вид:
Таблица 2. Автоматный
вид
| Входные сигналы |
Выходные сигналы |
| 0010 |
1111 |
| 0110 |
1110 |
| 1111 |
1000 |
| 1101 |
1000 |
| 00100000 |
11110011 |
| 1010 |
1011 |
| 0011 |
1110 |
| 1110 |
1001 |
1.3 Построение графа переходов абстрактного автомата
Построим по таблице 2
граф переходов автомата. При этом предполагается, что последний символ каждого
входного слова должен переводит автомат в начальное состояние.
Граф переходов
абстрактного автомата представлен в приложении 1.
1.4 Минимизация абстрактного автомата
По графу переходов
построим таблицу переходов-выходов заданного автомата (таблица 3).
Таблица 3. Таблица
переходов-выходов автомата
| a(t-1) |
0 |
1 |
|
a0
|
a1/1
|
a2/1
|
|
a1
|
a3/1
|
a4/1
|
|
a2
|
a10/0
|
a11/0
|
|
a3
|
- |
a5/1
|
|
a4
|
- |
a6/1
|
|
a5
|
a8/1
|
a9/0
|
|
a6
|
a8/0
|
- |
|
a7
|
a0/-
|
a0/-
|
|
a8
|
a0/-
|
a0/-
|
|
a9
|
a0/-
|
a0/-
|
|
a10
|
- |
a12/1
|
|
a11
|
a14/0
|
a15/0
|
|
a12
|
a13/1
|
- |
|
a13
|
a0/-
|
a0/-
|
|
a14
|
- |
a16/0
|
|
a15
|
a17/1
|
a18/0
|
|
a16
|
a0/-
|
a0/-
|
|
a17
|
a0/-
|
a0/-
|
|
a18
|
a0/-
|
a0/-
|
Один из алгоритмов
минимизации полностью определенных автоматов заключается в следующем. Множество
состояний исходного абстрактного автомата разбивается на попарно пересекающиеся
классы эквивалентных состояний, далее каждый класс эквивалентности заменяется
одним состоянием. В результате получается минимальный автомат, имеющий столько
же состояний, на сколько классов эквивалентности разбиваются исходные состояния
автомата.
0 класс
эквивалентности:
|
a0, a1
|
b0
|
|
a2, a11
|
b1
|
|
a14
|
b2
|
|
a3, a4,
a10
|
b3
|
|
a5, a15
|
b4
|
|
a6
|
b5
|
|
a7, a8,
a9, a13, a16, a17, a18
|
b6
|
|
a12
|
b7
|
1
класс
эквивалентности:
|
a0
|
c0
|
|
a1
|
c1
|
|
a2
|
c2
|
|
a3
|
c3
|
|
a4
|
c4
|
|
a5, a15
|
c5
|
|
a6
|
c6
|
|
a10
|
c7
|
|
a11
|
c8
|
|
a12
|
c9
|
|
a14
|
c10
|
|
a7, a8,
a9, a13, a16, a17, a18
|
c11
|
2 класс
эквивалентности:
|
a0
|
d0
|
|
a1
|
d1
|
|
a2
|
d2
|
|
a3
|
d3
|
|
a4
|
d4
|
|
a5, a15
|
d5
|
|
a6
|
d6
|
|
a10
|
d7
|
|
a11
|
d8
|
|
a12
|
d9
|
|
a14
|
d10
|
|
a7, a8,
a9, a13, a16, a17, a18
|
d11
|
Из разбиения видно, что
классы 1 и 2 совпадают, значит, продолжать не имеет смысла.
Таблица
переходов-выходов минимизированного автомата представлена в таблице 4:
Таблица 4. Таблица
переходов-выходов минимизированного автомата
| d(t-1) |
0 |
1 |
|
d0
|
d1/1
|
d2/1
|
|
d1
|
d3/1
|
d4/1
|
|
d2
|
d7/0
|
d8/0
|
|
d3
|
- |
d5/1
|
|
d4
|
- |
d6/1
|
|
d5
|
d11/1
|
d11/0
|
|
d6
|
d11/0
|
- |
|
d7
|
- |
d9/1
|
|
d8
|
d10/0
|
d5/0
|
|
d9
|
d11/1
|
- |
|
d10
|
- |
d11/0
|
|
d11
|
d0/-
|
d0/-
|
Граф переходов
минимизированного автомата представлен в приложении 2.
2.
СТРУКТУРНЫЙ
СИНТЕЗ КОНЕЧНОГО АВТОМАТА
2.1
Кодирование состояний, входных и выходных сигналов
Для кодирования
состояний, входных и выходных сигналов конечного автомата, необходимо вычислить
число элементов памяти:
а)
рассчитаем число элементов памяти: Н = ] log2h [, где h - число
состояний после минимизации D = {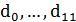 } }
H = ] log2 12 [ = 4
б) рассчитаем
число входных (L) и выходных
(М) шин:
L = ] log2n[
М
=] log2m [,
где
n, m - число букв
входного и выходного алфавитов
Z = {0, 1} L = ] log2 2 [ = 1
W = {0, 1} M = ] log2 2 [ = 1
Из приведённого выше
следует, что для кодирования состояний необходимо 4 элемента памяти, обозначим
их Q0, …, Q3.
Закодируем состояния (таблица 5) случайными кодами.
Таблица 5. Таблица кодированных состояний
| d(t-1) |
Q0
|
Q1
|
Q2
|
Q3
|
|
d0
|
0 |
0 |
0 |
0 |
|
d1
|
0 |
0 |
0 |
1 |
|
d2
|
0 |
0 |
1 |
0 |
|
d3
|
0 |
0 |
1 |
1 |
|
d4
|
0 |
1 |
0 |
0 |
|
d5
|
0 |
1 |
0 |
1 |
|
d6
|
0 |
1 |
1 |
0 |
|
d7
|
0 |
1 |
1 |
1 |
|
d8
|
1 |
0 |
0 |
0 |
|
d9
|
1 |
0 |
0 |
1 |
|
d10
|
1 |
0 |
1 |
0 |
|
d11
|
1 |
0 |
1 |
1 |
2.2 Формирование функций
возбуждения и выходных сигналов структурного автомата
По минимизированному
графу переходов
абстрактного автомата (Приложение 2) можно составить таблицу
переходов, выходных сигналов и сигналов возбуждения D-триггеров автомата
Мили (таблица
6), Т-триггеров автомата Мили (таблица
7), RS-триггеров
(таблица 8), JK-триггеров
(таблица 9).
D-триггер
– элемент задержки – имеет один информационный вход D
и один выход Q и осуществляет
задержку поступившего на его вход сигнала на один такт. Состояние, в которое
переходит триггер, совпадает с поступившим на его вход сигналом D(t).
Таблица 6. Таблица
переходов, выходных сигналов и сигналов возбуждения D-триггеров
| Номер перехода |
Исходное состояние |
Код исходного состояния |
Следующее состояние |
Код следующего состояния |
Входной набор |
Выходные сигналы |
Сигналы возбуждения |
| 0 |
1 |
D3
|
D2
|
D1
|
D0
|
| 1 |
d0
|
0000 |
d1
d2
|
0001
0010
|
0
1
|
|
d00
d01
|
|
|
d01
|
d00
|
| 2 |
d1
|
0001 |
d3
d4
|
0011
0100
|
0
1
|
|
d10
d11
|
|
d11
|
d10
|
d10
|
| 3 |
d2
|
0010 |
d7
d8
|
0111
1000
|
0
1
|
d20
d21
|
|
d21
|
d20
|
d20
|
d20
|
| 4 |
d3
|
0011 |
d5
|
0101 |
1 |
|
d31
|
|
d31
|
|
d31
|
| 5 |
d4
|
0100 |
d6
|
0110 |
1 |
|
d41
|
|
d41
|
d41
|
|
| 6 |
d5
|
0101 |
d11
|
1011 |
0Ú1 |
d50
|
d51
|
d50Ú
d51
|
|
d50
Ú
d51
|
d50
Ú
d51
|
| 7 |
d6
|
0110 |
d11
|
1011 |
0 |
d60
|
|
d60
|
|
d60
|
d60
|
| 8 |
d7
|
0111 |
d9
|
1001 |
1 |
|
d71
|
d71
|
|
|
d71
|
| 9 |
d8
|
1000 |
d10
d5
|
1010
0101
|
0
1
|
d80
d81
|
|
d80
|
d81
|
d80
|
d81
|
| 10 |
d9
|
1001 |
d11
|
1011 |
0 |
|
d90
|
d90
|
|
d90
|
d90
|
| 11 |
d10
|
1010 |
d11
|
1011 |
1 |
d101
|
|
d101
|
|
d101
|
d101
|
| 12 |
d11
|
1011 |
d0
|
0000 |
- |
- |
- |
- |
- |
- |
- |
Из таблицы следует, что
выходные сигналы автомата Мили описываются следующими выражениями:
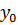 = d20
Úd21
Úd50
Úd60
Úd80
Úd81
Úd101=
d2 Úd50
Úd60
Úd8
Úd101 = d20
Úd21
Úd50
Úd60
Úd80
Úd81
Úd101=
d2 Úd50
Úd60
Úd8
Úd101
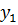 = d00
Úd01
Úd10
Úd11
Úd31
Úd41
Úd51
Úd71
Úd90=
d0 Úd1
Úd31
Úd41
Úd51
Úd71
Úd90 = d00
Úd01
Úd10
Úd11
Úd31
Úd41
Úd51
Úd71
Úd90=
d0 Úd1
Úd31
Úd41
Úd51
Úd71
Úd90
Также следует, что
сигналы возбуждения D-триггеров
автомата Мили описываются следующими выражениями:
D3
= d21
Úd50
Úd51
Úd60
Úd71
Úd80
Úd90
Úd101=
d21
Úd5
Úd60
Úd71
Úd80
Úd90
Úd101
D2
= d11 Úd20 Úd31
Úd41
Úd81
D1
= d01
Úd10
Úd20
Úd41
Úd50
Úd51
Úd60
Úd80
Úd90
Úd101=
=d01
Úd10
Úd20
Úd41
Ú
d5Ú d60
Úd80
Úd90
Úd101
D0
= d00
Úd10
Úd20
Úd31
Úd50
Úd51
Úd60
Úd71
Úd81
Úd90
Úd101=
=d00
Úd10
Úd20
Úd31
Úd5
Úd60
Úd71
Úd81
Úd90
Úd101
Функциональная схема
автомата Мили на D-триггерах,
построенная по выражениям, описывающим выходные сигналы, приведена в Приложении
3.
Таблица 7. Таблица
переходов, выходных сигналов и сигналов возбуждения T-триггеров
| Номер перехода |
Исходное состояние |
Код исходного состояния |
Следующее состояние |
Код следующего состояния |
Входной набор |
Выходные сигналы |
Сигналы возбуждения |
| 0 |
1 |
T3
|
T2
|
T1
|
T0
|
| 1 |
d0
|
0000 |
d1
d2
|
0001
0010
|
0
1
|
|
d00
d01
|
|
|
d01
|
d00
|
| 2 |
d1
|
0001 |
d3
d4
|
0011
0100
|
0
1
|
|
d10
d11
|
|
d11
|
d10
|
d11
|
| 3 |
d2
|
0010 |
d7
d8
|
0111
1000
|
0
1
|
d20
d21
|
|
d21
|
d20
|
d21
|
d20
|
| 4 |
d3
|
0011 |
d5
|
0101 |
1 |
|
d31
|
|
d31
|
d31
|
|
| 5 |
d4
|
0100 |
d6
|
0110 |
1 |
|
d41
|
|
|
d41
|
|
| 6 |
d5
|
0101 |
d11
|
1011 |
0Ú1 |
d50
|
d51
|
d50
Ú
d51
|
d50
Ú
d51
|
d50
Ú
d51
|
|
| 7 |
d6
|
0110 |
d11
|
1011 |
0 |
d60
|
|
d60
|
d60
|
|
d60
|
| 8 |
d7
|
0111 |
d9
|
1001 |
1 |
|
d71
|
d71
|
d71
|
d71
|
|
| 9 |
d8
|
1000 |
d10
d5
|
1010
0101
|
0
1
|
d80
d81
|
|
d81
|
d81
|
d80
|
d81
|
| 10 |
d9
|
1001 |
d11
|
1011 |
0 |
|
d90
|
|
|
d90
|
|
| 11 |
d10
|
1010 |
d11
|
1011 |
1 |
d101
|
|
|
|
|
d101
|
| 12 |
d11
|
1011 |
d0
|
0000 |
- |
- |
- |
- |
- |
- |
- |
Из таблицы следует, что
сигналы возбуждения T-триггеров
автомата Мили описываются следующими выражениями:
T3
= d21 Úd50 Úd51
Úd60
Úd71
Úd81=
d21 Ú d5 Úd60
Úd71
Úd81
T2
= d11 Úd20 Úd31
Úd50
Úd51
Úd60
Úd71
Úd81=
d11 Úd20 Úd31
Úd5
Úd60
Úd71
Úd81
T1
= d01 Úd10 Úd21
Úd31
Úd41
Úd50
Úd51
Úd71
Úd80
Úd90=
d01 Úd10 Úd21
Úd31
Úd41
Úd5
Úd71
Úd80
Úd90
T0
=
d00
Úd20
Úd60
Úd81
Úd101
Функциональная схема
автомата Мили на T-триггерах,
построенная по выражениям, описывающим выходные сигналы, приведена в Приложении
4.
Таблица 8. Таблица
переходов и сигналов возбуждения RS-триггеров
| Номер перехода |
Сигналы возбуждения |
|
R3
|
S3
|
R2
|
S2
|
R1
|
S1
|
R0
|
S0
|
| 1 |
|
|
|
|
|
d01
|
|
d00
|
| 2 |
|
|
|
d11
|
|
d10
|
d11
|
|
| 3 |
|
d21
|
|
d20
|
d21
|
|
|
d20
|
| 4 |
|
|
|
d31
|
d31
|
|
|
|
| 5 |
|
|
|
|
|
d41
|
|
|
| 6 |
|
d50
Ú
d51
|
d50
Ú
d51
|
|
|
d50
Ú
d51
|
|
|
| 7 |
|
d60
|
d60
|
|
|
|
|
d60
|
| 8 |
|
d71
|
d71
|
|
d71
|
|
|
|
| 9 |
d81
|
|
|
d81
|
|
d80
|
|
d81
|
| 10 |
|
d90
|
|
|
|
|
|
|
| 11 |
|
|
|
|
|
|
|
d101
|
| 12 |
- |
- |
- |
- |
- |
- |
-
|
- |
Из таблицы следует, что
сигналы возбуждения RS-триггеров
автомата Мили описываются следующими выражениями:
R3
= d81
S3
= d21 Úd50 Úd51
Úd60
Úd71
Úd90=
d21 Úd5 Úd60
Úd71
Úd90
R2
= d50 Úd51 Úd60
Úd71=
d5 Úd60
Úd71
S2
= d11 Úd20 Úd31
Úd81
R1
=
d21
Úd31
Úd71
S1
= d01 Úd10 Úd41
Úd50
Úd51
Úd80=
d01 Úd10 Úd41
Úd5
Úd80
R0
=
d11
S0
=
d00
Úd20
Úd60
Úd81
Úd101
Функциональная
схема автомата Мили на RS-триггерах,
построенная по выражениям, описывающим выходные сигналы, приведена в Приложении
5.
Таблица 9. Таблица
переходов и сигналов возбуждения JK-триггеров
| Номер перехода |
Сигналы возбуждения |
|
J3
|
K3
|
J2
|
K2
|
J1
|
K1
|
J0
|
K0
|
| 1 |
|
|
|
|
d01
|
|
d00
|
|
| 2 |
|
|
d11
|
|
d10
|
|
|
d11
|
| 3 |
d21
|
|
d20
|
|
|
d21
|
d20
|
|
| 4 |
|
|
d31
|
|
|
d31
|
|
|
| 5 |
|
|
|
|
d41
|
|
|
|
| 6 |
d50
Ú
d51
|
|
|
d50
Ú
d51
|
d50
Ú
d51
|
|
|
|
| 7 |
d60
|
|
|
d60
|
|
|
d60
|
|
| 8 |
d71
|
|
|
d71
|
|
d71
|
|
|
| 9 |
|
d81
|
d81
|
|
d80
|
|
d81
|
|
| 10 |
d90
|
|
|
|
|
|
|
|
| 11 |
|
|
|
|
|
|
d101
|
|
| 12 |
- |
- |
- |
- |
- |
- |
- |
-
|
Из таблицы следует, что
сигналы возбуждения RS-триггеров
автомата Мили описываются следующими выражениями:
J3
= d21 Úd50 Úd51
Úd60
Úd71
Úd90=
d21 Úd5 Úd60
Úd71
Úd90
K3
= d81
J2
= d11 Úd20 Úd31
Úd81
K2
= d50 Úd51 Úd60
Úd71=
d5 Úd60 Úd71
J1
= d01 Úd10 Úd41
Úd50
Úd51
Úd80=
d01 Úd10 Úd41
Úd5
Úd80
K1
= d21 d31 d71
J0
= d00
Úd20
Úd60
Úd81
Úd101
K0
=
d11
Функциональная схема
автомата Мили на JK-триггерах,
построенная по выражениям, описывающим выходные сигналы, приведена в Приложении
6.
ЗАКЛЮЧЕНИЕ
В процессе выполнения
работы мной были закреплены знания о синтезе конечных автоматов и получена
практика в построении комбинационных схем.
В данной работе мной было
выполнено проектирование конечного автомата по алфавитному отображению с
использованием канонического метода структурного синтеза автоматов. Построены
граф переходов абстрактного автомата с 17 состояниями и таблицы
переходов-выходов. Минимизация состояний автомата выполнена путем разбиения на
группы эквивалентных между собой состояний. После чего был построен минимальный
граф Мили с 11 состояниями. Выполнен структурный синтез конечного автомата.
Построены функциональные схемы автомата Мили на D, T, RS и JK-триггерах.
СПИСОК
ЛИТЕРАТУРЫ
1.
Баранов С.И. Синтез микропрограммных автоматов (граф-схемы и автоматы).
– 2-е изд., перераб. и доп. – Л.: Энергия, 1979. – 232 с., ил.
2.
Дегтярев
В.М., Ерош И.Л., Михайлов В.В. Проектирование цифровых автоматов.-Л.:ЛИАП,
1974г.
3.
Козин И.В.,
Иванов Н.М., Лупал А.М. Проектирование управляющих автоматов по алфавитному
отображению. Учебное пособие по курсовому проектированию/ЛИАП. – Л., 1991. – 82
с., ил.
4.
Лупал А.М. Теория
автоматов. Учебное пособие/СПбГУАП. – СПб., 2000. – 120 с., ил.
5.
Лысиков Б.Г.
Арифметические и логические основы цифровых автоматов. Учебник для вузов по
спец. «Электронные вычислительные машины». – 2-е изд., перераб. и доп. – Мн.:
Выш. школа, 1980. – 336 с., ил.
6.
Конспект лекций
по дисциплине «Теория автоматов», преподаватель Глебов Е.А., 2005-2006 уч.г.
|