Контрольная работа: Вычисление наибольшей прибыли предприятия
Контрольная работа: Вычисление наибольшей прибыли предприятия
Содержание
Задача 1. 2
Задача 2. 4
Задача 3. 6
Задача
1
Пусть х (млн. шт.) –
объем производства, С(х)=2х3-7х и D(x)=2х2+9х+15
– соответственно функция издержек и доход некоторой фирмы. При каком значении х
фирма получит наибольшую прибыль π(х)? какова эта прибыль?
Решение
Прибыль фирмы является
разницей между доходом и издержками фирмы:
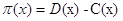 , ,
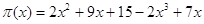 , ,
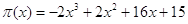 . .
Найдем наибольшее
значение прибыли путем нахождения максимума функции 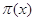 . .
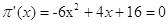
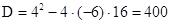
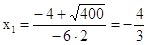 - не
удовлетворяет условию задачи, - не
удовлетворяет условию задачи,
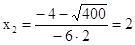 . .
График функции прибыли представлен
на рисунке 1.
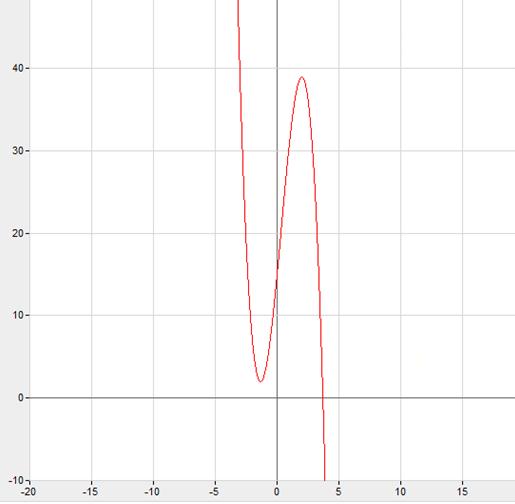
Рисунок 1 - График
функции прибыли 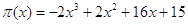
Как видно из рисунка 1,
функция прибыли 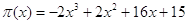 в точке х=2 достигает
максимального значения. Следовательно, фирма получает наибольшую прибыль при
объеме производства 2 млн. шт. и эта прибыль составляет: в точке х=2 достигает
максимального значения. Следовательно, фирма получает наибольшую прибыль при
объеме производства 2 млн. шт. и эта прибыль составляет:
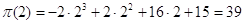 млн.
у.е. млн.
у.е.
Ответ: наибольшую
прибыль фирма получит при объеме производства 2 млн. шт. и эта прибыль составит
39 млн. у.е.
Задача
2
Заданы: функция прибыли
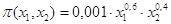 , где х1 и х2
– объемы некоторых ресурсов; цены р1=1 и р2=1 за единицу
каждого ресурса соответственно (в некоторых у.е.); бюджетное ограничение I=150
на затраты по приобретению указанных ресурсов (в тех же у.е.). При каких
значениях объемов используемых ресурсов фирма–производитель получит наибольшую
прибыль? , где х1 и х2
– объемы некоторых ресурсов; цены р1=1 и р2=1 за единицу
каждого ресурса соответственно (в некоторых у.е.); бюджетное ограничение I=150
на затраты по приобретению указанных ресурсов (в тех же у.е.). При каких
значениях объемов используемых ресурсов фирма–производитель получит наибольшую
прибыль?
Решение
Задача сводится к
поиску максимума функции 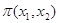 при
существовании ограничения при
существовании ограничения 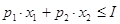 : :
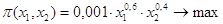
при 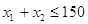 . .
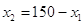 , ,
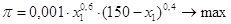 . .
Найдем максимум функции
графически.
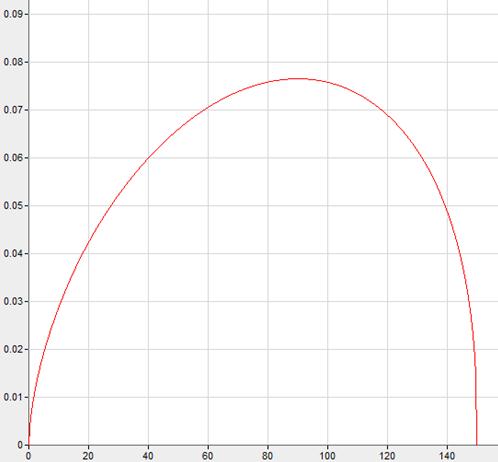
Рисунок 2 – График
функции 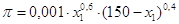
Как видно, функция
достигает максимального значения при х1=90.
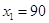 , ,
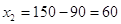 . .
Ответ:
фирма–производитель получит наибольшую прибыль при объемах ресурсов х1=90
и х2=60.
Задача
3
Задана парная выборка
из 10 пар значений случайных велbчин
X и Y
(таблица 1).
Таблица 1 – Исходные
данные
|
|
х |
у |
| 1 |
5 |
70 |
| 2 |
11 |
65 |
| 3 |
15 |
55 |
| 4 |
17 |
60 |
| 5 |
2 |
50 |
| 6 |
22 |
35 |
| 7 |
25 |
40 |
| 8 |
27 |
30 |
| 9 |
30 |
25 |
| 10 |
35 |
32 |
1)
Изобразите
корреляционное поле случайных величин X
и Y.
2)
Вычислите
основные числовые характеристики случайных величин X
и Y: их математические ожидания и
дисперсии, средние квадратические отклонения и размах вариации.
3)
Найдите
их совместные числовые характеристики: ковариацию, коэффициент корреляции.
4)
С
помощью найденных характеристик составьте уравнение линейной регрессии Y
на X.
5)
Составьте
уравнение линейной регрессии X
на Y.
6)
Нанесите
найденные уравнения на корреляционное поле; найдите точку пересечения полученных
линий регрессии.
7)
Вычислите
стандартные ошибки коэффициентов регрессии b0
и b1.
8)
Проверьте
гипотезы о статистической значимости коэффициентов регрессии b0
и b1.
9)
Вычислите
с надежностью 0,95 интервальные оценки коэффициентов b0
и b1
регрессии Y на X.
10)
Найдите
коэффициент детерминации R2
и поясните смысл полученного результата.
Решение.
1)
Корреляционное
поле случайных величин X
и Y
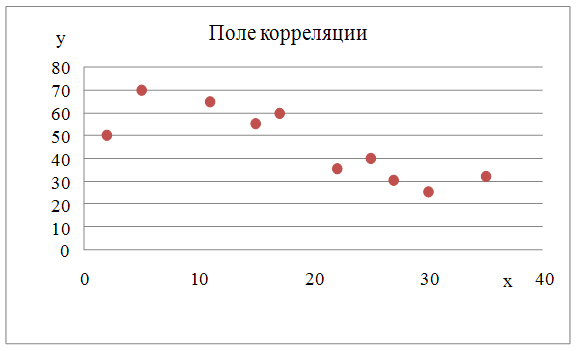
2)
Основные
числовые характеристики случайных величин X
и Y: их математические ожидания и
дисперсии, средние квадратические отклонения и размах вариации
Таблица 2 –
Вспомогательные расчеты
|
|
х |
у |
х2
|
y2
|
xy |
| 1 |
5 |
70 |
25 |
4900 |
350 |
| 2 |
11 |
65 |
121 |
4225 |
715 |
| 3 |
15 |
55 |
225 |
3025 |
825 |
| 4 |
17 |
60 |
289 |
3600 |
1020 |
| 5 |
2 |
50 |
4 |
2500 |
100 |
| 6 |
22 |
35 |
484 |
1225 |
770 |
| 7 |
25 |
40 |
625 |
1600 |
1000 |
| 8 |
27 |
30 |
729 |
900 |
810 |
| 9 |
30 |
25 |
900 |
625 |
750 |
| 10 |
35 |
32 |
1225 |
1024 |
1120 |
| сумма |
189 |
462 |
4627 |
23624 |
7460 |
| средн |
18,9 |
46,2 |
462,7 |
2362,4 |
746 |
Математическое
ожидание:
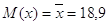 , ,
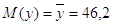 . .
Дисперсия:
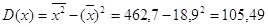 , ,
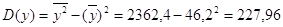 . .
Среднеквадратическое
отклонение:
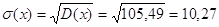 , ,
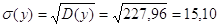 . .
Размах вариации:
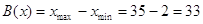 , ,
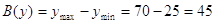 . .
3)
Совместные
числовые характеристики: ковариацию, коэффициент корреляции
Ковариация:
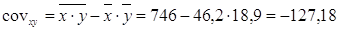 . .
Коэффициент корреляции:
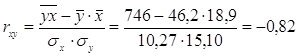 . .
4)
Уравнение
линейной регрессии Y на X
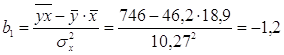 , ,
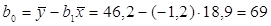 , ,
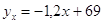 . .
5)
Уравнение
линейной регрессии X на Y
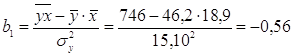 , ,
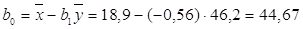 , ,
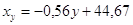 . .
6)
Нанесите
найденные уравнения на корреляционное поле; найдите точку пересечения
полученных линий регрессии
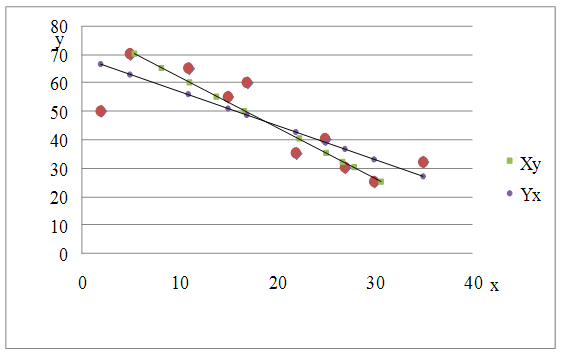
Точка пересечения (18,4;46,9).
7)
Стандартные
ошибки коэффициентов регрессии b0
и b1
Таблица 3 –
Вспомогательные расчеты
|
|
х |
у |
x' |
y' |
x-xcp
|
y-ycp
|
(x-xcp)2
|
(y-ycp)2
|
| 1 |
5 |
70 |
5,572 |
62,975 |
-13,028 |
16,775 |
169,7288 |
281,4006 |
| 2 |
11 |
65 |
8,3645 |
55,745 |
-10,2355 |
9,545 |
104,7655 |
91,10702 |
| 3 |
15 |
55 |
13,9495 |
50,925 |
-4,6505 |
4,725 |
21,62715 |
22,32562 |
| 4 |
17 |
60 |
11,157 |
48,515 |
-7,443 |
2,315 |
55,39825 |
5,359225 |
| 5 |
2 |
50 |
16,742 |
66,59 |
-1,858 |
20,39 |
3,452164 |
415,7521 |
| 6 |
22 |
35 |
25,1195 |
42,49 |
6,5195 |
-3,71 |
42,50388 |
13,7641 |
| 7 |
25 |
40 |
22,327 |
38,875 |
3,727 |
-7,325 |
13,89053 |
53,65563 |
| 8 |
27 |
30 |
27,912 |
36,465 |
9,312 |
-9,735 |
86,71334 |
94,77023 |
| 9 |
30 |
25 |
30,7045 |
32,85 |
12,1045 |
-13,35 |
146,5189 |
178,2225 |
| 10 |
35 |
32 |
26,795 |
26,825 |
8,195 |
-19,375 |
67,15803 |
375,3906 |
| сумма |
189 |
462 |
188,643 |
462,255 |
2,643 |
0,255 |
711,7565 |
1531,748 |
| средн |
18,9 |
46,2 |
18,8643 |
46,2255 |
0,2643 |
0,0255 |
71,17565 |
153,1748 |
Для линии регрессии Y
на X:
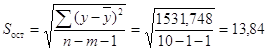 , ,
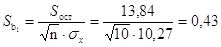 , ,
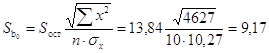 . .
Для линии регрессии X
на Y:
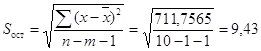 , ,
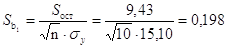 , ,
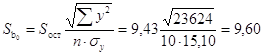 . .
8)
Проверка
гипотезы о статистической значимости коэффициентов регрессии b0
и b1
Для α=0,05
и k=n-1-1=8
значение критерия Стьюдента t=2,31
Для линии регрессии Y
на X:
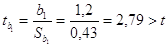 , коэффициент
значим, , коэффициент
значим,
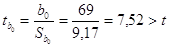 , коэффициент
значим. , коэффициент
значим.
Для линии регрессии X
на Y:
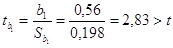 , коэффициент
значим, , коэффициент
значим,
 , коэффициент
значим. , коэффициент
значим.
9)
Вычисляем
с надежностью 0,95 интервальные оценки коэффициентов b0
и b1
регрессии Y на X
Доверительный интервал
для b0:
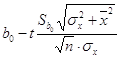 <a0< <a0<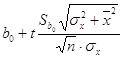 , ,
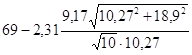 <a0< <a0<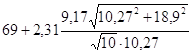 , ,
54,97<a0<83,03.
Доверительный интервал
для b1:
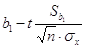 <a1< <a1<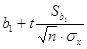 , ,
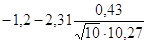 <a1< <a1<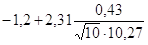 , ,
-1,23<a1<-1,17.
10)
Коэффициент
детерминации R2
:
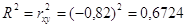 . .
Коэффициент
детерминации R2=0,6724
показывает, что вариация параметра Y
на 67,24% объясняется фактором Х. Доля влияния неучтенных факторов – 32,76%.
|