Дипломная работа: Решения задачи планирования производства симплекс методом
Дипломная работа: Решения задачи планирования производства симплекс методом
Федеральное агентство по образованию
Санкт-Петербургский Государственный Политехнический Университет
Факультет технической кибернетики
Кафедра «Системный анализ и управление»
Работа допущена к защите
Заведующий кафедрой
____________ В.Н. Козлов
«___» __________ 2010 г.
ДИПЛОМНАЯ РАБОТА
Тема: Решения задачи планирования производства симплекс методом.
Специальность:230201 – Информационные системы и технологии
Выполнил студент гр. 6082/2
Дегтярёв И.В.
Руководитель, к.т.н.,
доцент Болотин И.В.
Санкт-Петербург
2010
Санкт-Петербургский государственный политехнический университет
Факультет технической кибернетики
Кафедра «Системный анализ и управление»
УТВЕРЖДАЮ
«___» ____________2010 г.
Зав. кафедрой _______________
ЗАДАНИЕ
по дипломному проектированию
студенту Дегтярёву И.В.
группа 6082/2
1. Тема проекта (работы)______________________________________
_________________________________________________________________________________________________________________________________
2. Срок сдачи студентом
законченного проекта (работы)___________________________________________________________
3. Исходные данные к
проекту (работе)_________________________
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Содержание
расчетно-пояснительной записки (перечень подлежащих разработке вопросов)___________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
5. Перечень графического
материала (с точным указанием обязательных чертежей)________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6. Консультанты по проекту
(с указанием относящихся к ним разделов проекта, работы)___________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7. Дата выдачи задания________________________________________
Руководитель_________________________________________________
Задание принял к
исполнению___________________________________
Реферат
Дипломная работа представлена
на 94 страницах машинописного текста, содержит 15 рисунков, 9 таблиц, 11
наименований использованных источников.
В данной дипломной работе
решается задача планирования производства, являющаяся общей задачей линейного
программирования (ЛП). Для решения поставленной задачи использовался
симплекс-метод, т.к. он является наиболее известным, достаточно эффективным и
широко применяемым на практике для решения прикладных задач линейного
программирования. Во вспомогательных целях была использована надстройка MS
Excel «Поиск решения».
Так же в среде объектно-ориентированного
программирования С++ была реализована программа для решения задач линейного
программирования симплекс-методом (в частности поставленной задачи планирования
производства).
Перечень используемых
сокращений
ЛП – Линейное
программирование;
ЦЛП – Целочисленное
линейное программирование;
ЗЛП – Задача линейного
программирования;
ОДР – Область допустимых
решений;
MS Excel – Microsoft
Excel;
ОС – Операционная система
Содержание
Введение
1. Обзор
научно-технической литературы
1.1 История
развития экономико-математического планирования
1.2
Необходимость решения задач линейного
программирования
1.3 Линейное
программирование
1.4 Математическая формулировка задачи линейного
программирования
1.5
Постановка задачи целочисленного программирования
2. Обзор
основных алгоритмов решения задач ЛП
2.1
Целочисленное линейное программирование - метод отсечений Гомори
2.1.1
Отсечения
2.1.2
Описание алгоритма
2.2
Целочисленное линейное программирование - метод ветвей и границ
2.2.1 Общее
описание
2.2.2
Применение
2.2.3
Алгоритм решения
2.3 Симплекс
метод
2.3.1
Описание
2.3.2
Алгоритм симплекс-метода
2.3.2.1
Усиленная постановка задачи
2.3.2.2
Алгоритм
2.4 Решение
задач оптимизации при помощи средства «Поиск решения» в
Microsoft Excel
2.4.1
Описание
2.4.2
Процедура поиска решения
2.4.3
Параметры средства «Поиск решения»
3. Задача
планирования производства
3.1
Постановка задачи планирования производства в общем случае
3.2 Математическое описание поставленной задачи планирования симплекс
методом
3.3 Решение
поставленной задачи планирования производства
3.3.4
Проверка признака допустимости и оптимальности базиса
3.3.5
Нахождение разрешающего элемента в симплекс-таблице. Формирование нового базиса
3.3.6 Пересчет симплекс-таблицы
3.4
Результат решения задачи планирования производства
4. Программа
для решения задач ЛП симплекс методом
4.1 Описание
4.2
Графическое представление программы
4.3 Работа с
программой
4.4 Схема
программы
Заключение
Список
литературы
Введение
В процессе хозяйственной
деятельности сырьевая база предприятия занимает одно из центральных мест,
поэтому вопрос об оптимизации сырья на предприятии при планировании выпускаемой
продукции актуален в настоящее время.
Актуальность данной темы
также заключается в том, что в процессе производственной деятельности все
предприятия сталкиваются с проблемой нехватки сырья, а также с тем, что выпускаемая
продукция должна быть адекватна с экономической точки зрения, другими словами,
чтобы её можно было выгодно продать, и чтобы она соответствовала запросам
покупателя.
Учитывая всевозрастающую
ограниченность ресурсов, очень важно добиваться их максимально эффективного
использования. План должен быть разработан настолько умело, чтобы использование
ограниченных ресурсов было оптимальным.
Существует много причин,
заставляющих промышленные предприятия заниматься оптимизацией структуры сырья:
улучшение финансовых
показателей;
повышение уровня
производства;
наращивание объемов
производства.
Планирование выпуска
продукции также имеет огромное значение для предприятия, оно тесно
взаимосвязано с сырьевой базой предприятия.
Сущность планирования
продукции состоит в обосновании целей и способов их достижения на основе
выявления комплекса задач и работ, а также определения эффективных методов и
способов, ресурсов всех видов, необходимых для выполнения этих задач и
установления их взаимодействия.
Оптимизация структуры сырья
при планировании выпуска продукции является существенным источником резервов
увеличения суммы прибыли. Логично предположить, что предприятию выгодно
увеличивать доли тех изделий, которые приносят максимальную прибыль. Но всегда
следует помнить о ряде ограничений, не позволяющих отказаться от менее
рентабельной продукции:
1) Потенциальный спрос на
продукцию достаточно динамичен и дифференцирован во времени и пространстве. Те
изделия и торговые марки, которые востребованы в данный момент времени, могут потерять
свою потребительскую привлекательность через некоторые промежутки времени;
2) Основные
производственные фонды нуждаются в постоянной эксплуатации, наладке и
обслуживании. Простои оборудования – это всегда неблагоприятный фактор для
производства.
Планом выпуска продукции
определяются:
Количественные показатели
производства;
Объем реализации,
ожидаемый в планируемом периоде. Этот показатель определяется на основе объема
выпуска продукции и ожидаемой средней цены реализации 1 учетной единицы
продукции. Ожидаемая средняя цена реализации определяется на основе
ретроспективного анализа данных за предыдущие несколько лет с учетом ожидаемых
и текущих темпов инфляции.
Для каждого периода,
охватываемого планом, необходимо определить две переменные: объём производства
в данный период; количество ресурсов, используемых в данный период.
План выпуска продукции
отражает номенклатуру и ассортимент производства продукции в соответствии с
планом реализации, обязательствами предприятия и экономическими условиями.
Планирование выпускаемой
продукции включает решение ряда задач. Прежде всего, планируется номенклатура,
ассортимент и объем выпуска продукции. Номенклатура производства представляет
собой перечень изделий (готовых изделий, полуфабрикатов и т. п.), подлежащих изготовлению
на предприятии в плановом периоде. Ассортимент продукции характеризует
соотношение удельных весов отдельных видов изделий в общем, выпуске продукции.
Номенклатура, ассортимент и объем изготовляемой предприятием продукции
устанавливаются на основе централизованного задания по поставкам важнейших
видов продукции и портфеля заказов предприятия с учетом его специализации. При
этом учитываются и договоры по кооперированным поставкам, заключенные
предприятием.
Целесообразно
совершенствовать структуру выпуска только той продукции, удельный вес которой в
общем объеме выпуска достаточно высок.
Необходимым условием
увеличения количества производства определенных изделий является
универсальность оборудования для их производства.
План выпуска продукции
может повлиять на величину целого ряда издержек, в том числе: издержки хранения
готовой продукции; издержки ведения портфеля отложенных заказав; издержки,
связанные с внеурочной работой или простоем работников; издержки, связанные с
передачей части работ субподрядчикам; издержки, связанные с наймом и
увольнением работников.
Задача оптимизации
структуры сырья при планировании выпуска продукции должна решаться на каждом
промышленном предприятии, которое заинтересовано в максимизации прибыли от
продажи выпускаемой продукции. Такая задача является задачей линейного
программирования.
Данная дипломная работа
состоит из теоретической и практической частей. В теоретической части
рассматривается алгоритм решения оптимизационной задачи линейного
программирования. В практической части рассматривается задача планирования
производства выпускающего несколько видов продукции из ограниченного количества
ресурсов для достижения максимальной прибыли. Так же реализуется программный
интерфейс в среде объектно-ориентированного программирования С++, для решения
поставленной задачи симплекс методом.
1.
Обзор научно-технической литературы
1.1
История развития экономико-математического планирования
В 1938-1939 гг.
ленинградский математик (впоследствии академик, лауреат Ленинской,
Государственных и Нобелевской премий) Л.В. Канторович в результате анализа ряда
проблем организации и планирования производства сформулировал новый класс
условно-экстремальных задач и предложил методы их решения. Так было положено
начало новой отрасли прикладной математики линейному программированию. В более
поздних работах Л. В. Канторович расширил область применения линейного
программирования в социалистической экономике, сформулировав задачи отраслевого
и народнохозяйственного оптимального планирования. А через два десятилетия
после своего возникновения линейное программирование стало основным
инструментом плановоэкономических решений на всех уровнях социалистического
народного хозяйства.
В том же 1939 г. ленинградский экономист В. В. Новожилов, рассматривая эффективность плановых и проектных
решений, сформулировал важные теоретические положения, ставшие потом
органической частью теории оптимального планирования социалистической экономики.
Далее методы планирования
продолжали совершенствоваться, но только развитие вычислительной техники в
конце 50-х гг. позволило сделать плановые многовариантные расчеты достаточно
распространенными. Важную роль в организации и пропаганде экономико-математических
исследований в этот период сыграл академик В. С. Немчинов. Именно в эти годы
получают развитие некоторые разделы прикладной математики, связанные с решением
оптимизационных задач: линейное и нелинейное программирование, теория
оптимального управления и др. В 60-е гг. основное внимание исследователей
сосредоточивается на разработке оптимизационных моделей различных типов и их
практическом применении к решению задач планирования. Было построено большое
количество экономико-математических моделей, на основе которых проведены
расчеты по составлению реальных оптимальных планов (оптимальные планы
перевозок, эксплуатации подвижного состава транспорта, использования топлива,
загрузки оборудования предприятий; оптимальное размещение отдельных отраслей промышленности
и предприятий отрасли; оптимальное планирование и распределение
капиталовложений и т. д.), что дало большой народнохозяйственный эффект. Наряду
с расширением сферы применения математических моделей в экономике и
планировании осуществляется процесс усовершенствования моделей и использования
более адекватного математического аппарата: переход от статических моделей к
динамическим, от жестко детерминированных к стохастическим моделям, учитывающим
случайность и неопределенность экономических процессов, применение дискретного
программирования, методов статистического моделирования, создание новых
алгоритмов, позволяющих решать задачи большой размерности.
1.2
Необходимость решения задач линейного программирования
Применение
экономико-математических методов и моделей позволяет существенно улучшить
качество планирования и получить дополнительный экономический эффект без
вовлечения в общественное производство дополнительных ресурсов, что чрезвычайно
важно в условиях перехода экономики на преимущественно интенсивный путь
развития.
В настоящее время область
возможного применения экономико-математических методов в планировании
чрезвычайно велика и с каждым годом она расширяется. Однако область
фактического их применения в практике плановых расчетов намного скромнее. Это
объясняется трудностями широкого внедрения экономико-математических методов.
К числу их следует
отнести: сложность определения критерия оптимальности в ряде экономических
задач; трудности при решении проблемы «встраивания» математических моделей в
существующую систему планирования и управления, приводящие к необходимости
создания новой технологии планирования, базирующегося на системном
использовании экономико-математических методов и ЭВМ; стохастический и
динамический характер экономических процессов, требующий усложнения
используемого математического аппарата и программного обеспечения ЭВМ,
увеличения объема вычислений; трудность измерений многих экономических явлений
и получения массовой достоверной информации для наполнения разработанных
моделей; трудность проверки правильности (верификации) экономикоматематических
моделей, ориентированных не столько на подтверждение действительности, сколько
на решение новых социально-экономических задач (это в первую очередь относится
к моделям планирования и прогнозирования), и т. д.
Но главная трудность
заключается в сложности моделируемых экономических процессов и явлений.
Большинство объектов, изучаемых экономической наукой, может быть
охарактеризовано кибернетическим понятием «сложная система». При изучении
систем недостаточно (а иногда и невозможно) пользоваться методом расчленения на
элементы с последующим изучением этих элементов в отдельности.
Кроме того, моделирование
существенно усложняется тем, что экономика охватывает не только
производственные процессы, но и производственные отношения. Моделировать производственные
отношения невозможно, не учитывая поведение людей, их интересы и индивидуально
принятые решения.
В результате
производственно-хозяйственная или социально-экономическая ситуация, в которой
приходится принимать плановые решения, часто оказывается намного богаче и
сложнее тех моделей, которые используются в планировании в этой ситуации.
В настоящее время линейное
программирование является одним из наиболее употребительных аппаратов
математической теории оптимального принятия решений, в том числе и в финансовой
математике. Для решения задач линейного программирования разработано сложное
программное обеспечение, дающее возможность эффективно и надежно решать практические
задачи больших объемов. Эти программы и системы снабжены развитыми системами
подготовки исходных данных, средствами их анализа и представления полученных
результатов. В развитие и совершенствование этих систем вложен труд и талант
многих математиков, аккумулирован опыт решения тысяч задач. Владение аппаратом
линейного программирования необходимо каждому специалисту в области прикладной
математики.
Линейное программирование
представляет собой наиболее часто используемый метод оптимизации. К числу задач
линейного программирования можно отнести задачи:
рационального
использования сырья и материалов; задачи оптимального раскроя;
оптимизации
производственной программы предприятий;
оптимального размещения и
концентрации производства;
составления оптимального
плана перевозок, работы транспорта;
управления
производственными запасами;
и многие другие,
принадлежащие сфере оптимального планирования.
Для большого количества
практически интересных задач целевая функция выражается линейно – через
характеристики плана, причем допустимые значения параметров подчинены линейным
равенствам или неравенствам. Нахождение при данных условиях абсолютного
экстремума целевой функции носит название линейного программирования.
Первым исследованием по
линейному программированию является работа Л. В. Канторовича “Математические
методы организации и планирования производства”, опубликованная в 1939 г. В нем дана постановка задач линейного программирования, разработан метод разрешающих
множителей решения задач линейного программирования и дано его теоретическое
обоснование.
Прямая задача линейного
программирования является математической формулировкой проблемы составления
такого плана использования различных способов производства, который позволяет
получить максимальное количество однородного продукта при имеющихся в наличии
ресурсах.
Математическое
программирование – это прикладная отрасль математики, которая является
теоретической основой решения задач оптимального планирования.
Существуют следующие
разделы математического программирования: линейное, параметрическое, нелинейное
и динамическое программирование. Наиболее разработанным и широко применяемым
разделом математического программирования является линейное программирование,
целью которого служит отыскивание оптимума (max, min) заданной линейной функции
при наличии ограничений в виде линейных уравнений или неравенств.
1.3
Линейное программирование
Линейное программирование
— математическая дисциплина, посвященная теории и методам решения задач об
экстремумах линейных функций на множествах n-мерного векторного пространства,
задаваемых системами линейных уравнений и неравенств.
Линейное программирование
является частным случаем выпуклого программирования, которое в свою очередь является
частным случаем математического программирования. Одновременно оно — основа
нескольких методов решения задач целочисленного и нелинейного программирования.
Одним из обобщений линейного программирования является дробно-линейное
программирование.
Многие свойства задач
линейного программирования можно интерпретировать также как свойства
многогранников и таким образом геометрически формулировать и доказывать их.
Термин «программирование»
нужно понимать в смысле «планирования». Он был предложен в середине 1940-х
годов Джорджем Данцигом, одним из основателей линейного программирования, еще
до того, как компьютеры были использованы для решения линейных задач
оптимизации.
1.4
Математическая формулировка задачи линейного программирования
Нужно определить максимум
линейной целевой функции (линейной формы)
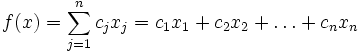
при условиях
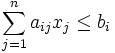 при при 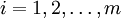 . .
Иногда на xi также
накладывается некоторый набор ограничений в виде равенств, но от них можно
избавиться, последовательно выражая одну переменную через другие и подставляя
ее во всех остальных равенствах и неравенствах (а также в функции f).
Такую задачу называют
"основной" или "стандартной" в линейном программировании.
1.5
Постановка задачи целочисленного программирования
По смыслу значительной
части экономических задач, относятся к задачам линейного программирования,
компоненты решения должны выражаться в целых числах, т.е. быть целочисленными.
К ним относятся, например, задачи, в которых переменные означают количество
единиц неделимой продукции, число станков при загрузке оборудования, число
судов при распределениях по линиям, число турбин в энергосистеме, число
вычислительных машин в управляющем комплексе и многие другие.
Задача линейного
целочисленного программирования формируется следующим образом: найти такое
решение (план) X = (x1,x2,...,xn), при котором линейная функция
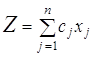 (1) (1)
принимает максимальное или
минимальное значение при ограничениях
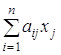 =bi, i=1, 2…,m. (2) =bi, i=1, 2…,m. (2)
хj ³ 0, j=1, 2,...,n.(3)
xj — целые числа (4)
2.
Обзор основных алгоритмов решения задач ЛП
2.1
Целочисленное линейное программирование - метод отсечений Гомори
Целочисленное линейное
программирование (сокращенно ЦЛП) занимается задачами линейного
программирования с целочисленными переменными, общая задача формулируется
следующим образом: найти maxАх ≤ b; х - целочисленный. ЦЛП может
рассматриваться так же, как поиск точки решетки, принадлежащей многограннику
или как решение системы линейных уравнений с целыми неотрицательными
переменными. Иными словами, в ЦЛП рассматриваются совместные ограничения
неотрицательность и целочисленность.
2.1.1
Отсечения
С помощью отсечений
выделяют целочисленные части полиэдров. Метод отсечений был разработан в конце
1950-х годов Гомори для решения целочисленных линейных программ с помощью
симплекс-метода. Метод отсечений оказался полезным и с теоретической точки
зрения он дает возможность описать целочисленную оболочку полиэдра.
Далее описывается метод
отсечений Гомори, дающий алгоритм решения задач целочисленного линейного
программирования. Данный метод, который также носит название метода отсекающих
плоскостей, предназначен для решения ЦЗЛП (целочисленной задачи линейного
программирования) в канонической форме.
Описываемая ниже версия
алгоритма предназначена для решения полностью целочисленных задач, т.е. таких,
у которых все параметры aij, cj, bi – целые.
2.1.2
Описание алгоритма
Приведем обобщенную схему
алгоритма Гомори. Структурно он делится на так называемые большие итерации. Каждая
большая итерация содержит этапы:
1.Сначала задача решается
методами линейного программирования (малые итерации), обычно симплекс-методом,
и анализируется результат, если результатом являются целые числа, то на этом
решение заканчивается, а если дробные, то производят следующие операции:
2. В оптимальном плане
(симплекс-таблице) выбирают строку, в которой целая часть дробного(!)
свободного члена (P0) принимает наибольшее значение.
3.Построение для найденной
компоненты условия отсечения.
Исходя из уравнения по
данной строке xr=P0r - ar,1*x1 - … - ar,n*xn в систему ограничений добавляем
неравенство, в котором коэффициенты будут дробными частями коэффициентов
данного уравнения:
{P0r} –{ar,1}*x1 - … -{ar,n}*xn
≤ 0.
Переводим к каноническому
виду добавляя новую переменную xn+1, получим:
{P0r} –{ ar,1}*x1 - … -
{ar,n}*xn+xn+1= 0
И соответственно добавляем
в симплекс-таблицу новый базисный вектор по новой переменной xn+1.
4.Переход на начало
следующей большой итерации.
Замечание:
При добавлении в симплекс-таблицу
нового базисного вектора по новой переменной xn+1 мы получаем недопустимое
(отрицательное) решение. Для того, чтобы избавиться от недопустимого решения
выбираем столбец замещения так, чтобы строкой замещения стала новая добавленная
строка по переменной xn+1. Продолжаем пересчет симплекс-таблицы. Если снова
получаем дробное решение, то еще вводим дополнительный базисный вектор, и так
до получения целочисленного решения. Но следует заметить, что если область
допустимых решений очень мала, то она может и не содержать целых значений, это
необходимо проверить графически. Если область допустимых решений не содержит
целочисленного решения, то в применении метода Гомори нет необходимости, целого
решения не будет!
2.2
Целочисленное линейное программирование - метод ветвей и границ
Метод ветвей и границ —
общий алгоритмический метод для нахождения оптимальных решений различных задач
оптимизации, особенно дискретной и комбинаторной оптимизации. По существу,
метод является комбинаторным (алгоритм перебора) с отсевом подмножеств
множества допустимых решений, не содержащих оптимальных решений. Его суть
заключается в упорядоченном переборе вариантов и рассмотрении лишь тех из них,
которые оказываются по определенным признакам перспективными, и отбрасывании
бесперспективных вариантов.
Метод ветвей и границ
состоит в следующем: множество допустимых решений (планов) некоторым способом
разбивается на подмножества, каждое из которых этим же способом снова
разбивается на подмножества. Процесс продолжается до тех пор, пока не получено
оптимальное целочисленное решение исходной задачи.
Метод был впервые
предложен Ленд и Дойг в 1960 г. для решения задач целочисленного линейного
программирования.
2.2.1
Общее описание
Общая идея метода может
быть описана на примере поиска минимума и максимума функции f(x) на множестве
допустимых значений x. Функция f и x могут быть произвольной природы. Для
метода ветвей и границ необходимы две процедуры: ветвление и нахождение оценок
(границ).
Процедура ветвления
состоит в разбиении области допустимых решений на подобласти меньших размеров.
Процедуру можно рекурсивно применять к подобластям. Полученные подобласти
образуют дерево, называемое деревом поиска или деревом ветвей и границ. Узлами
этого дерева являются построенные подобласти.
Процедура нахождения
оценок заключается в поиске верхних и нижних границ для оптимального значения
на подобласти допустимых решений.
В основе метода ветвей и
границ лежит следующая идея (для задачи минимизации): если нижняя граница для
подобласти A дерева поиска больше, чем верхняя граница какой-либо ранее
просмотренной подобласти B, то A может быть исключена из дальнейшего
рассмотрения (правило отсева). Обычно, минимальную из полученных верхних оценок
записывают в глобальную переменную m; любой узел дерева поиска, нижняя граница
которого больше значения m, может быть исключен из дальнейшего рассмотрения.
Если нижняя граница для
узла дерева совпадает с верхней границей, то это значение является минимумом
функции и достигается на соответствующей подобласти.
2.2.2
Применение
Метод используется для
решения некоторых NP-трудных задач, такие как:
Задача коммивояжера
Задача о ранце
2.2.3
Алгоритм решения
Первоначально находим
симплексным методом или методом искусственного базиса оптимальный план задачи
без учета целочисленности переменных. Пусть им является план X0. Если среди
компонент этого плана нет дробных чисел, то тем самым найдено искомое решение
данной задачи и Fmax = F(Xo).
Если же среди компонент
плана X0 имеются дробные числа, то X0 не удовлетворяет условию целочисленности
и необходимо осуществить упорядоченный переход к новым планам, пока не будет
найдено решение задачи. Покажем, как это можно сделать, предварительно отметив,
что F(X0) ³ F(X)
для всякого последующего плана X.
Предполагая, что найденный
оптимальный план X0 не удовлетворяет условию целочисленности переменных, тем
самым считаем, что среди его компонент есть дробные числа. Пусть, например,
переменная 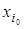 приняла
в плане X0 дробное значение. Тогда в оптимальном целочисленном плане ее
значение будет по крайней мере либо меньше или равно ближайшему меньшему целому
числу приняла
в плане X0 дробное значение. Тогда в оптимальном целочисленном плане ее
значение будет по крайней мере либо меньше или равно ближайшему меньшему целому
числу 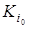 ,
либо больше или равно ближайшему большему целому числу ,
либо больше или равно ближайшему большему целому числу 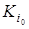 +1. Определяя эти числа, находим
симплексным методом решение двух задач линейного программирования: +1. Определяя эти числа, находим
симплексным методом решение двух задач линейного программирования:
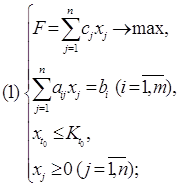
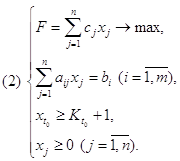
Найдем решение задач
линейного программирования (I) и (II). Очевидно, здесь возможен один из
следующих четырех случаев:
1. Одна из задач неразрешима,
а другая имеет целочисленный оптимальный план. Тогда этот план и значение
целевой функции на нем и дают решение исходной задачи.
2. Одна из задач
неразрешима, а другая имеет оптимальный план, среди компонент которого есть
дробные числа. Тогда рассматриваем вторую задачу и в ее оптимальном плане
выбираем одну из компонент, значение которой равно дробному числу, и строим две
задачи, аналогичные задачам (I) и (II).
3. Обе задачи разрешимы.
Одна из задач имеет оптимальный целочисленный план, а в оптимальном плане
другой задачи есть дробные числа. Тогда вычисляем значения целевой функции на
этих планах и сравниваем их между собой. Если на целочисленном оптимальном
плане значение целевой функции больше или равно ее значению на плане, среди
компонент которого есть дробные числа, то данный целочисленный план является
оптимальным для исходной задачи и он вместе со значением целевой функции на нем
дает искомое решение.
Если же значение целевой
функции больше на плане, среди компонент которого есть дробные числа, то
следует взять одно из таких чисел и для задачи, план которой рассматривается,
необходимо построить две задачи, аналогичные (I) и (II).
4. Обе задачи разрешимы, и
среди оптимальных планов обеих задач есть дробные числа. Тогда вычисляем
значение целевой функции на данных оптимальных планах и рассматриваем ту из
задач, для которой значение целевой функции является наибольшим. В оптимальном
плане этой задачи выбираем одну из компонент, значение которой является дробным
числом, и строим две задачи, аналогичные (I) и (II).
Таким образом, описанный
выше итерационный процесс может быть представлен в виде некоторого дерева, на
котором исходная вершина отвечает оптимальному плану Х0 задачи (1)-(3), а
каждая соединенная с ней ветвью вершина отвечает оптимальным планам задач (I) и
(II). Каждая из этих вершин имеет свои ветвления. При этом на каждом шаге
выбирается та вершина, для которой значение функции является наибольшим. Если
на некотором шаге будет получен план, имеющий целочисленные компоненты, и
значение функции на нем окажется больше или равно, чем значение функции в
других возможных для ветвления вершинах, то данный план является оптимальным
планом исходной задачи целочисленного программирования и значение целевой
функции на нем является максимальным.
Итак, процесс нахождения
решения задачи целочисленного программирования (1)-(4) методом ветвей и границ
включает следующие основные этапы:
1). Находят решение задачи
линейного программирования (1)-(3).
2). Составляют
дополнительные ограничения для одной из переменных, значение которой в
оптимальном плане задачи (1)-(3) является дробным числом.
3). Находят решение задач
(I) и (II), которые получаются из задачи (1)-(3) в результате присоединения
дополнительных ограничений.
4). В случае необходимости
составляют дополнительные ограничения для переменной, значение которой является
дробным, формулируют задачи, аналогичные задачам (I) и (II), и находят их
решение.
Итерационный процесс
продолжают до тех пор, пока не будет найдена вершина, соответствующая
целочисленному плану задачи (1)-(3) и такая, что значение функции в этой
вершине больше или равно значению функции в других возможных для ветвления
вершинах.
Описанный выше метод
ветвей и границ имеет более простую логическую схему расчетов, чем метод
Гомори.
В узлах метода ветвей и
границ используется симплекс-метод.
Главный недостаток
алгоритма метода ветвей и границ заключается в необходимости полностью решать
задачи линейного программирования, ассоциированные с каждой из вершин
многогранника допустимых решений. Для задач большой размерности это требует
значительных и, в известной степени, неоправданных с практической точки зрения
затрат времени.
2.3
Симплекс метод
Задачи линейного
программирования в канонической форме широко распространены в инженерной
практике, и для их решения разработана большая группа методов, основной из
которых — симплекс-метод. Рассмотрим постановку и решение задачи линейного
программирования в канонической форме.
2.3.1
Описание
Задача будет
рассматриваться в форме, которая называется канонической. Известно, что путем
введения дополнительных ограничений и переменных можно свести к канонической
форме задачу линейного программирования, представленную в любой форме, в
частности в естественной форме.
2.3.2
Алгоритм симплекс-метода
2.3.2.1
Усиленная постановка задачи
Задачи линейного
программирования имеет следующий вид:
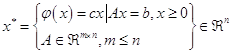
с помощью
конечно-сходящейся вычислительной процедуры симплекс-метода, заданной
оператором
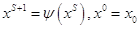
В операторе векторы 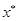 и и 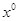 — оптимальное
решение задачи и начальное приближение для симплекс-метода, которые в
симплекс-методе являются базисными решениями, определяемыми ниже. Векторы — оптимальное
решение задачи и начальное приближение для симплекс-метода, которые в
симплекс-методе являются базисными решениями, определяемыми ниже. Векторы 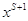 и и 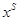 представляют
собой последующее и предыдущее решения в симплекс-методе. представляют
собой последующее и предыдущее решения в симплекс-методе.
2.3.2.2
Алгоритм
Алгоритм симплекс-метода
формулируется для задачи линейного программирования следующим образом:
Шаг 1. Формулировка задачи
линейного программирования в канонической форме на основе метода искусственного
базиса, так чтобы в матрице ограничений существовала единичная базисная
матрица. Для этого необходимо дополнить матрицу ограничений единичными
столбцами, которые должны в совокупности с исходными столбцами матрицы
ограничений обеспечивать существование единичной базисной матрицы. При этом
естественным образом должны быть введены соответствующие искусственные
переменные, которые включаются в целевую функцию с большими положительными
весовыми коэффициентами для задачи на минимум. В результате запишем исходную
матрицу ограничений 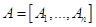 . в симплекс-таблицу(*), а
коэффициенты целевой функции . в симплекс-таблицу(*), а
коэффициенты целевой функции 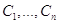 запишем в строку этой таблицы. В
таблицу(*) также включим компоненты исходного базисного решения, определяемого
вектором запишем в строку этой таблицы. В
таблицу(*) также включим компоненты исходного базисного решения, определяемого
вектором 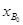
Таблица (*)
| #№ |
Базисные столбцы |
Bs |
Базисное решение Xs |
C1 |
C2 |
… |
Cm |
Cm+1 |
… |
Ck |
… |
Cn |
| A1 |
A2 |
… |
Am |
Am+1 |
… |
Ak |
… |
An |
| 1 |
A1 |
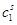
|
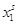
|
1 |
0 |
… |
0 |
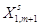
|
… |
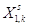
|
… |
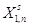
|
| 2 |
A2 |
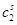
|
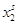
|
0 |
1 |
… |
0 |
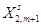
|
… |
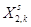
|
… |
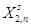
|
| … |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
| l |
Al |
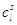
|
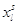
|
0 |
0 |
… |
0 |
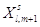
|
… |
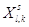
|
… |
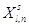
|
| … |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
| m |
Am |
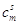
|
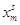
|
0 |
0 |
… |
1 |
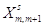
|
… |
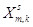
|
… |
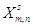
|
|
|
|
|
Оценки |
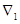
|
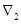
|
… |
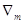
|
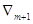
|
… |
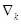
|
… |
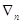
|
Шаг 2. Вычисление
характеристических разностей (оценок) по формулам и запись оценок в 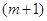 -ю строку
симплекс-таблицы. -ю строку
симплекс-таблицы.
Шаг 3. Вычисление оценки 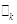 , удовлетворяющей
условию: , удовлетворяющей
условию:
Если все 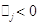 , то в соответствии с
выполнением критерия оптимальности вектор , то в соответствии с
выполнением критерия оптимальности вектор 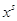 — оптимальное решение, и далее
следует перейти к шагу 9, иначе — к шагу 4. — оптимальное решение, и далее
следует перейти к шагу 9, иначе — к шагу 4.
Шаг 4. Вычисление нового
базисного решения 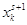 из условия: из условия:
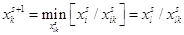
Шаг 5. Вычисление
компонент нового базисного решения 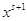 по формулам: по формулам:
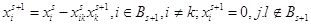
Шаг 6. Вычисление
элементов новой симплекс-таблицы для 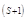 -й итерации метода по формулам: -й итерации метода по формулам:
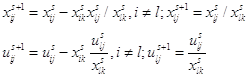
Шаг 7. Корректировка
симплекс-таблицы с учетом изменений коэффициентов целевой функции,
соответствующих новому базисному решению. Формируем таблицу (**).
Таблица (**)
| #№ |
Базисные столбцы |
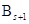
|
Базисное решение Xs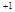
|
C1 |
C2 |
… |
Cm |
m+1 |
… |
Ck |
… |
Cn |
| A1 |
A2 |
… |
Am |
Am+1 |
… |
Ak |
… |
An |
| 1 |
A1 |
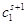
|
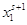
|
1 |
0 |
… |
0 |
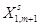
|
… |
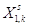
|
… |
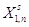
|
| 2 |
A2 |
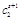
|
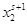
|
0 |
1 |
… |
0 |
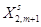
|
… |
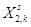
|
… |
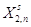
|
| … |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
| l |
Al |
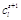
|
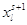
|
0 |
0 |
… |
0 |
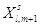
|
… |
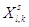
|
… |
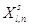
|
| … |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
| m |
Am |
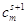
|
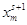
|
0 |
0 |
… |
1 |
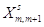
|
… |
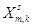
|
… |
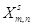
|
|
|
|
|
Оценки |
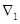
|
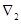
|
… |
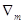
|
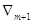
|
… |
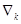
|
… |
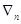
|
     Шаг
8. Переход к шагу 2. Шаг
8. Переход к шагу 2.
Шаг 9. Остановка,
регистрация оптимального решения.
Таким образом,
сформулированный алгоритм определяет конечную последовательность шагов, необходимых
для вычисления оптимального решения.
2.4
Решение задач оптимизации при помощи средства «Поиск решения» в Microsoft Excel
Мощным средством анализа
данных MS Excel является надстройка Solver (Поиск решения). С ее помощью можно
определить, при каких значениях указанных влияющих ячеек формула в целевой
ячейке принимает нужное значение (минимальное, максимальное или равное
какой-либо величине). Для процедуры поиска решения можно задать ограничения,
причем не обязательно, чтобы при этом использовались те же влияющие ячейки. Для
расчета заданного значения применяются различные математические методы поиска.
Вы можете установить режим, в котором полученные значения переменных
автоматически заносятся в таблицу. Кроме того, результаты работы программы
могут быть оформлены в виде отчета.
2.4.1
Описание
Программа «Поиск решений»
(в оригинале Excel Solver) – дополнительная надстройка табличного процессора MS
Excel, которая предназначена для решения определенных систем уравнений,
линейных и нелинейных задач оптимизации, используется с 1991 года.
Размер задачи, которую
можно решить с помощью базовой версии этой программы, ограничивается такими
предельными показателями:
количество неизвестных
(decision variable) – 200;
количество формульных
ограничений (explicit constraint) на неизвестные – 100;
количество предельных
условий (simple constraint) на неизвестные – 400.
Разработчик программы
Solver, компания Frontline System, уже давно специализируется на разработке
мощных и удобных способов оптимизации, встроенных в среду популярных табличных
процессоров разнообразных фирм-производителей (MS Excel Solver, Adobe Quattro
Pro, Lotus 1-2-3).
Высокая эффективность их
применения объясняется интеграцией программы оптимизации и табличного
бизнес-документа. Благодаря мировой популярности табличного процессора MS Excel
встроенная в его среду программа Solver является наиболее распространенным
инструментом для поиска оптимальных решений в сфере современного бизнеса.
Средство поиска решения
Microsoft Excel использует алгоритм нелинейной оптимизации Generalized Reduced
Gradient (GRG2), разработанный Леоном Ласдоном (Leon Lasdon, University of
Texas at Austin) и Аланом Уореном (Allan Waren, Cleveland State University),
алгоритмы симплексного метода и метода «branch-and-bound» для решения линейных
и целочисленных задач с ограничениями разработаны Джоном Уотсоном (John Watson)
и Деном Филстра (Dan Fylstra) из Frontline Systems, Inc.
2.4.2
Процедура поиска решения
В меню «Сервис» в разделе
«Надстройки» необходимо активизировать функцию «Поиск решения».
Создайте таблицу с
формулами, которые устанавливают связи между ячейками. (см. Рис.1)
Выделите целевую ячейку,
которая должна принять необходимое значение, и выберите команду «Поиск
решения». Поле Set Target Cell (Установить целевую ячейку) открывшегося
диалогового окна надстройки Solver (Поиск решения) будет содержать адрес
целевой ячейки.
Установите переключатели
Equal To (Равной), задающие значение целевой ячейки, — Мах (максимальному
значению), Min (минимальному значению) или Value of (значению). В последнем
случае введите значение в поле справа.
Укажите в поле By Changing
Cells (Изменяя ячейки), в каких ячейках программа должна изменять значения в
поисках оптимального результата.
Создайте ограничения в
списке Subject to the Constraints (Ограничения). Для этого щелкните на кнопке
Add (Добавить) и в диалоговом окне Add Constraint (Добавление ограничения)
определите ограничение.
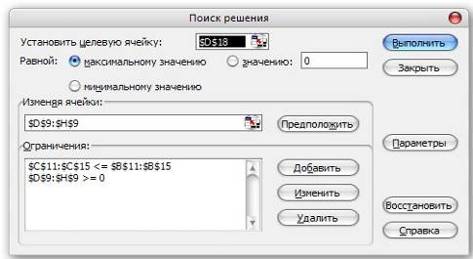
Рис.2 Диалоговое окно
надстройки «Поиск решения»
Щелкните на кнопке на
кнопке Options (Параметры), и в появившемся окне установите переключатель
Неотрицательные значения (если переменные должны быть позитивными числами),
Линейная модель (если задача, которую вы решаете, относится к линейным
моделям).
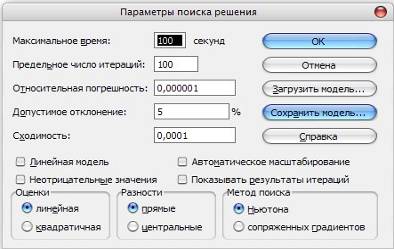
Рис.3 Окно параметров
надстройки «Поиск решения»
Щелкнув на кнопке Solver
(Выполнить), запустите процесс поиска решения.
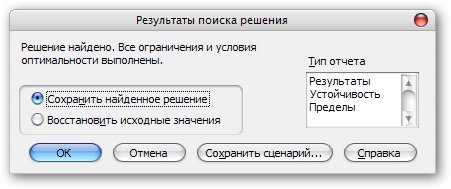
Рис.4 Результаты поиска
решения
2.4.3
Параметры средства «Поиск решения»
Максимальное время - служит
для ограничения времени, отпущенного на поиск решения задачи. В этом поле можно
ввести время в секундах, не превышающее 32 767 (примерно девять часов);
значение 100, используемое по умолчанию, вполне приемлемо для решения
большинства простых задач.
Предельное число итераций
- управляет временем решения задачи путем ограничения числа вычислительных
циклов (итераций).
Относительная погрешность
- определяет точность вычислений. Чем меньше значение этого параметра, тем выше
точность вычислений.
Допустимое отклонение -
предназначен для задания допуска на отклонение от оптимального решения, если
множество значений влияющей ячейки ограничено множеством целых чисел. Чем
больше значение допуска, тем меньше времени требуется на поиск решения.
Сходимость - применяется
только к нелинейным задачам. Когда относительное изменение значения в целевой
ячейке за последние пять итераций становится меньше числа, указанного в поле
Сходимость, поиск прекращается.
Линейная модель - служит
для ускорения поиска решения путем применения к задаче оптимизации линейной
модели. Нелинейные модели предполагают использование нелинейных функций, фактора
роста и экспоненциального сглаживания, что замедляет вычисления.
Неотрицательные значения -
позволяет установить нулевую нижнюю границу для тех влияющих ячеек, для которых
не было задано соответствующее ограничение в диалоговом окне Добавить ограничение.
Автоматическое
масштабирование - используется, когда числа в изменяемых ячейках и в целевой
ячейке существенно различаются.
Показывать результаты
итераций - приостанавливает поиск решения для просмотра результатов отдельных
итераций.
Загрузить модель - после
щелчка на этой кнопке отрывается одноименное диалоговое окно, в котором можно
ввести ссылку на диапазон ячеек, содержащих модель оптимизации.
Сохранить модель - служит
для отображения на экране одноименного диалогового окна, в котором можно ввести
ссылку на диапазон ячеек, предназначенный для хранения модели оптимизации.
Оценка линейная - выберите
этот переключатель для работы с линейной моделью.
Оценка квадратичная -
выберите этот переключатель для работы с нелинейной моделью.
Разности прямые - используется
в большинстве задач, где скорость изменения ограничений относительно невысока.
Увеличивает скорость работы средства Поиск решения.
Разности центральные -
используется для функций, имеющих разрывную производную. Данный способ требует
больше вычислений, однако его применение может быть оправданным, если выдано
сообщение о том, что получить более точное решение не удается.
Метод поиска Ньютона -
требует больше памяти, но выполняет меньше итераций, чем в методе сопряженных
градиентов.
Метод поиска сопряженных
градиентов - реализует метод сопряженных градиентов, для которого требуется
меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный
метод следует использовать, если задача достаточно большая и необходимо
экономить память или если итерации дают слишком малое отличие в
последовательных приближениях.
В результате исследования
основных алгоритмов решения задач ЛП, было принято решение поставленную задачу
планирования производства решать симплекс методом. Это обусловлено тем, что
симплекс метод является эффективным алгоритмом и наиболее универсальным методом,
которым можно решить любую задачу линейного программирования. В качестве
вспомогательного средства, для составления конкретной задачи планирования
производства (подбора таких значений, чтобы задача имела решение) было
использовано средство «Поиск решения» в MS Excel.
3.
Задача планирования производства
Задача планирования
производства относится к категории экономических проектов, к которым
предъявлены определенные требования. Проект - это ограниченное по времени
целенаправленное изменение отдельной системы с установленными требованиями к
качеству результатов, возможными рамками расхода средств и ресурсов и
специфической организацией.
3.1 Постановка задачи
планирования производства в общем случае
Некоторое предприятие
производит n типов продукции, затрачивая при этом m типов ресурсов. Известны
следующие параметры: aij – количество i-го ресурса, необходимое для
производства единичного количества j-й продукции; aij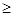 0 (i=1,…,m; j=1,…,n); 0 (i=1,…,m; j=1,…,n);
bi-запас i-го ресурса на
предприятии, bi>0;
cj-цена единичного
количества j-й продукции, cj>0.
Предполагается, что
затраты ресурсов растут прямо пропорционально объему производства. Пусть xj –
планируемый объем производства j-й продукции. Тогда допустимым является только
такой набор производимой продукции x=(x1,x2,…,xn), при котором суммарные
затраты каждого вида i-го ресурса не превосходят его запаса:
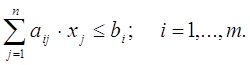 (1) (1)
Кроме того, имеем
следующее ограничение: xj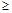 0; j=1,…,n. (2) 0; j=1,…,n. (2)
Стоимость набора продукции
x выражается величиной: 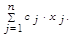 (3) (3)
Задача планирования
производства ставится следующим образом: среди всех векторов x, удовлетворяющим
ограничениям (1), (2), найти такой, при котором величина (3) принимает
наибольшее значение.
3.2 Математическое описание
поставленной задачи планирования симплекс методом
Пусть некоторое
предприятие производит 5 видов продукции A, B, C, D и E, затрачивая при этом 5
типов ресурсов. На производство продукции типа A требуется следующее количество
имеющихся на предприятии ресурсов (дается количество каждого ресурса,
необходимого для производства единицы продукции типа A): 1 – количество ресурса
1, 4 – количество ресурса 2, 2 – количество ресурса 3, 1 – количество ресурса
4, 3 – количество ресурса 5. На производство единицы продукции типа B требуется
(в условных единицах): 2 – количество ресурса 1, 2 – количество ресурса 2, 1 –
количество ресурса 3, 4 – количество ресурса 4, 2 – количество ресурса 5. На
производство единицы продукции типа C требуется (в условных единицах): 4 –
количество ресурса 1, 1 – количество ресурса 2, 3 – количество ресурса 3, 1 –
количество ресурса 4, 2 – количество ресурса 5. На производство единицы
продукции типа D требуется (в условных единицах): 3 – количество ресурса 1, 2 –
количество ресурса 2, 4 – количество ресурса 3, 2 – количество ресурса 4, 1 –
количество ресурса 5. На производство единицы продукции типа E требуется (в
условных единицах): 1 – количество ресурса 1, 2 – количество ресурса 2, 1 –
количество ресурса 3, 4 – количество ресурса 4, 4 – количество ресурса 5.
Допустим, что запас
ресурса 1 на предприятии составляет 600 условных единиц, запас ресурса 2 – 590
условных единиц, запас ресурса 3 – 750 условных единиц, запас ресурса 4 – 670
условных единиц и запас ресурса 5 – 495 условных единиц.
Цена единицы продукции
типа A равна 60 рублям, цена единицы продукции типа B равна 50 рублям, цена
единицы продукции типа C равна 37 рублям, цена единицы продукции типа D равна
45 рублям, а единица продукции типа E – 56 рублям.
Нужно спланировать такой
набор производимой продукции x=(x1, x2, x3, x4, x5), при котором суммарные
затраты каждого вида ресурса не превосходят его запаса, т.е.
x1+4x2+2x3+1x4+3x5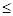 600; 600;
2x1+2x2+x3+4x4+2x5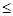 590; 590;
4x1+x2+3x3+x4+2x5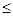 750; 750;
3x1+2x2+4x3+2x4+x5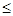 670; 670;
x1+2x2+x3+4x4+4x5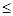 495; 495;
и при этом должны
выполняться следующие ограничения: x1, x2, x3, x4, x5 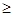 0. Спланированный набор
производимой продукции x=(x1, x2, x3, x4, x5) должен обеспечить максимум
стоимости данного набора 0. Спланированный набор
производимой продукции x=(x1, x2, x3, x4, x5) должен обеспечить максимум
стоимости данного набора
{60x1+50x2+37x3+45x4+56x5} max. max.
Таким образом, мы получим
однокритериальную задачу, которая является задачей линейного программирования
(ЗЛП). Она сводится к поиску экстремума линейной функции (данная функция
называется либо критерием, либо целевой функцией)
f(x)=60x1+50x2+37x3+45x4+56x5
при наличии системы
линейных неравенств, ограничивающих область изменения аргументов этой функции
x1+4x2+2x3+1x4+3x5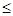 600; 600;
2x1+2x2+x3+4x4+2x5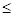 590; 590;
4x1+x2+3x3+x4+2x5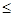 750; 750;
3x1+2x2+4x3+2x4+x5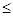 670; 670;
x1+2x2+x3+4x4+4x5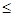 495; 495;
x1, x2, x3, x4, x5 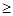 0. 0.
3.3
Решение поставленной задачи планирования производства
Описание метода решения
задачи.
Процедура решения ЗЛП
начинается с приведения ее к канонической форме, то есть к стандартной форме
задания, ориентированной на разработанный именно для этой формы метод решения.
Задача линейного программирования в канонической форме имеет смысл при условии
n>m. В этом случае полностью описывается область допустимых решений (ОДР)
ЗЛП, геометрически являющуюся выпуклым многогранником в евклидовом пространстве
Rn[1]. Выпуклая фигура, как известно, характеризуется тем свойством, что, если
две точки X1 и X2 принадлежат этой фигуре, то и весь отрезок X1X2 принадлежит
ей. Кроме того, доказано, что оптимальное решение ЗЛП всегда лежит на границе
ОДР. Поэтому справедлив вывод о том, что, по крайней мере, одна из угловых
(опорных) точек выпуклого многогранника ОДР является точкой оптимума. Для того,
чтобы определить координаты опорной точки, все множество переменных X={xj}, j=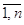 необходимо
разделить на два подмножества необходимо
разделить на два подмножества
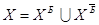 : :
подмножество базисных
переменных 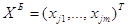 ,
при этом число m базисных переменных равно числу уравнений (ограничивается) при
условии, что уравнения являются линейно-независимыми; подмножество ,
при этом число m базисных переменных равно числу уравнений (ограничивается) при
условии, что уравнения являются линейно-независимыми; подмножество 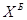 остальных n-m
свободных (внебазисных) переменных {xj}, j остальных n-m
свободных (внебазисных) переменных {xj}, j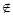 Б[1]. Б[1].
Количество возможных
вариантов разделения переменных на базисные и свободные (число базисов) равно 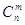 . .
Наиболее очевидный метод
решения ЗЛП состоит в том, чтобы для каждого из 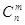 базисов найти координаты
соответствующих опорных точек, выделить из них точки, принадлежащие ОДР, а
затем из них, в свою очередь, выбрать ту, координаты которой максимизируют
целевую функцию. В отличие от этого метода, реализующего, по сути, идею полного
перебора опорных точек ОДР, известен более эффективный так называемый
симплекс-метод решения ЗЛП. базисов найти координаты
соответствующих опорных точек, выделить из них точки, принадлежащие ОДР, а
затем из них, в свою очередь, выбрать ту, координаты которой максимизируют
целевую функцию. В отличие от этого метода, реализующего, по сути, идею полного
перебора опорных точек ОДР, известен более эффективный так называемый
симплекс-метод решения ЗЛП.
В основе симплекс-метода
лежит подход, включающий:
выбор опорной точки,
принадлежащей ОДР (выбор начального допустимого базиса);
проверку опорной точки на
оптимальность;
выбор нового базиса,
позволяющего минимизировать число опорных точек на траектории в случае
невыполнения условий оптимальности.
Приведение исходной задачи
к каноническому виду.
Имеем исходную ЗЛП:
{60x1+50x2+37x3+45x4+56x5} max. max.
x1+4x2+2x3+x4+3x5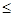 600; 600;
2x1+2x2+x3+4x4+2x5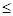 590; 590;
4x1+x2+3x3+x4+2x5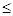 750;(4) 750;(4)
3x1+2x2+4x3+2x4+x5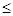 670; 670;
x1+2x2+x3+4x4+4x5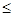 495; 495;
x1, x2, x3, x4, x5 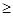 0. 0.
Приведем ЗЛП к
канонической форме. Приведение системы ограничений, заданных в форме
неравенств, к канонической форме равенств осуществляется посредством
соответствующего увеличения размерности вектора X=(x1, x2, x3, x4, x5) с учетом
обязательной неотрицательности всех его составляющих.
Таким образом, ЗЛП в
канонической форме имеет вид:
max {60x1+50x2+37x3+45x4+56x5};
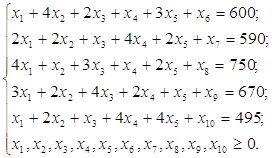 (5) (5)
Поиск допустимого базиса.
Заполнение
симплекс-таблицы.
ЗЛП в канонической форме
можно записать в матричном виде:
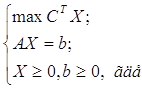 (6) (6)
b=(600, 590,
750, 670, 495)T,
X=(x1,
x2, x3, x4, x5, x6, x7, x8, x9, x10)T,
C=(60,50,37,45,56,0,0,0,0,0),
A=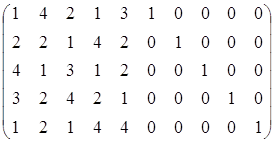 . .
Поиск допустимого базиса
начинается с анализа столбцов матрицы A=(A1, A2,…, A10), используемой в записи
ограничения (6) канонической формы ЗЛП. В качестве базисных следует выбирать
такие 5 переменных, которым соответствует набор столбцов, позволяющих составить
единичную матрицу P=(Aj1, Aj2, Aj3, Aj4, Aj5).
Если ОДР исходной ЗЛП
задана в форме неравенств типа 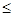 (как в нашем случае), то
начальный базис может быть сформирован из дополнительных переменных x6, x7, x8,
x9, x10, вводимых в систему ограничений с целью приведения ее к канонической
форме равенств. В этом случае матрица P будет единичной. (как в нашем случае), то
начальный базис может быть сформирован из дополнительных переменных x6, x7, x8,
x9, x10, вводимых в систему ограничений с целью приведения ее к канонической
форме равенств. В этом случае матрица P будет единичной.
Таким образом, выберем в
качестве начального базиса XБО=(x6, x7, x8, x9, x10)T, так как столбцы A6, A7,
A8, A9, A10 матрицы A образуют единичную матрицу.
Теперь перейдем к
заполнению симплекс-таблицы. Пусть ЗЛП сформулирована в канонической форме (5).
Мы выбрали базисные переменные x6, x7, x8, x9, x10. Разрешим систему неравенств
в (5) относительно базисных переменных.
Система ограничений в
форме Такера примет вид:
x6=600-(x1+4x2+2x3+x4+3x5);
x7=590-(2x1+2x2+x3+4x4+2x5);
x8=750-(4x1+x2+3x3+x4+2x5);(7)
x9=670-(3x1+2x2+4x3+2x4+x5);
x10=495-(x1+2x2+x3+4x4+4x5);
Целевую функцию можно
представить в виде:
f(x)=f0-(-60x1-50x2-37x3-45x4-56x5),
где f0=0.
Симплекс-таблица выглядит
следующим образом:
Таблица 1. Исходная симплекс
таблица в общем виде
|
|
b |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
x10 |
| x6 |
b6 |
a61 |
a62 |
a63 |
a64 |
a65 |
a66 |
a67 |
a68 |
a69 |
a610 |
| x7 |
b7 |
a71 |
a71 |
a71 |
a71 |
a71 |
a71 |
a71 |
a71 |
a71 |
a710 |
| x8 |
b8 |
a81 |
a82 |
a83 |
a84 |
a85 |
a86 |
a87 |
a88 |
a89 |
a810 |
| x9 |
b9 |
a91 |
a92 |
a93 |
a94 |
a95 |
a96 |
a97 |
a98 |
a99 |
a910 |
| x10 |
b10 |
a101 |
a102 |
a103 |
a104 |
a105 |
a106 |
a107 |
a108 |
a109 |
a1010 |
| f(x) |
f0 |
c1 |
c2 |
c3 |
c4 |
c5 |
c6 |
c7 |
c8 |
c9 |
c10 |
В нашем случае:
Таблица 2. Исходная симплекс
таблица поставленной задачи
| БП |
СЧ |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
X10 |
| X6 |
600 |
1 |
4 |
2 |
1 |
3 |
1 |
0 |
0 |
0 |
0 |
| X7 |
590 |
2 |
2 |
1 |
4 |
2 |
0 |
1 |
0 |
0 |
0 |
| X8 |
750 |
4 |
1 |
3 |
1 |
2 |
0 |
0 |
1 |
0 |
0 |
| X9 |
670 |
3 |
2 |
4 |
2 |
1 |
0 |
0 |
0 |
1 |
0 |
| X10 |
495 |
1 |
2 |
1 |
4 |
4 |
0 |
0 |
0 |
0 |
1 |
| Y |
0 |
-60 |
-50 |
-37 |
-45 |
-56 |
0 |
0 |
0 |
0 |
0 |
Составленная
симплекс-таблица соответствует начальному базису и начальной опорной точке ОДР.
Переход к очередной опорной точке в процессе поиска оптимального решения
сопровождается составлением новой симплекс-таблицы.
Каждая симплекс-таблица
анализируется по критериям допустимости и оптимальности базиса.
3.3.4
Проверка признака допустимости и оптимальности базиса
Признак допустимости
базиса:
в опорной точке в
соответствии с (7) xj=bi, i=6,…,10; j=6,…,10, поэтому признак допустимости
базиса формулируется как условие bi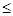 0, i=6,…,10. 0, i=6,…,10.
Признак оптимальности
базиса:
Если для 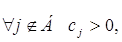 то найденное решение
оптимально и единственно. то найденное решение
оптимально и единственно.
Если для 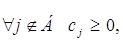 то найденное решение
оптимально, но не единственно. то найденное решение
оптимально, но не единственно.
Если 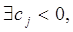 то решение
неоптимально. В этом случае поиск оптимального решения продолжается и
необходимо перейти к новой опорной точке. то решение
неоптимально. В этом случае поиск оптимального решения продолжается и
необходимо перейти к новой опорной точке.
Перейдем к конкретному случаю.
В нашем случае выполняется условие допустимости базиса, так как b=(600, 590,
750, 670, 495)T<0 и bi<0 (i=6,…,10).
Выбранный нами начальный
базис XБО=(x6, x7, x8, x9, x10)T не является оптимальным, так как c1=-60<0,
c2=-50<0, c3=-37<0, c4=-45<0 и c6=56<0. Таким образом, необходимо
осуществить переход к новой опорной точке (новому базису).
3.3.5
Нахождение разрешающего элемента в симплекс-таблице. Формирование нового базиса
В соответствии с
симплекс-методом новая опорная точка выбирается только среди соседних, то есть
новый базис лишь одной переменной отличается от прежнего. Таким образом,
формирование нового базиса осуществляется на базе прежнего посредством
выведения из него одной из базисных переменных xs и введения одной из свободных
переменных xr.
Выбор переменной xr. Выбор
переменной xr осуществляется по результатам анализа коэффициентов cj
симплекс-таблицы. Найдем cr=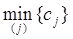 . .
В нашем случае min{c1, c2,
c3, c4, c5}=c1=-60 и xr=x1.
Столбец, который
соответствует переменной xr=x1 в симплекс-таблице, будем называть разрешающим.
Выбор переменной xs. Выбор
переменной xs проводится по результатам анализа коэффициентов air i=1,2,3,4,5
разрешающего столбца.
Если 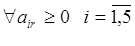 , это означает, что ОДР
такова, что неограниченное увеличение свободной переменной xr приводит к
неограниченному возрастанию целевой функции (ОДР не замкнута). , это означает, что ОДР
такова, что неограниченное увеличение свободной переменной xr приводит к
неограниченному возрастанию целевой функции (ОДР не замкнута).
Если 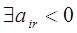 , то соответствующие
базисные переменные xi (i=6,7,8,9,10) получают отрицательные приращения при
увеличении xr=x1. Среди этих переменных xi необходимо отыскать xs, достигающую
нуля при минимальном значении приращения xr. Нужно найти , то соответствующие
базисные переменные xi (i=6,7,8,9,10) получают отрицательные приращения при
увеличении xr=x1. Среди этих переменных xi необходимо отыскать xs, достигающую
нуля при минимальном значении приращения xr. Нужно найти
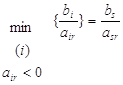 . .
В нашем случае min{600/1,
590/2, 750/4, 670/3, 495/1}=min{600,295,187.5,223.3,495}=187.5 и xs=x8. Строка,
которая соответствует переменной xs=x8 в симплекс-таблице, называется
разрешающей. Элемент asr=a81=4 называется разрешающим элементом
симплекс-таблицы.
Выбор разрешающего
элемента завершает формирование нового базиса XБ1, отличающегося от прежнего
базиса одной переменной xr=x1, то есть вместо переменной x8 в базис XБ1 будет
включена переменная x1: XБ1=(x6, x7, x1, x9, x10)T.
Для нового базиса (новой
опорной точки) снова заполняется симплекс-таблица, в которой новые базисные
переменные выражены через новые свободные.
3.3.6
Пересчет симплекс-таблицы
Правила пересчета:
Разрешающий элемент
заменяется на 1.
Элементы разрешающего
столбца за исключением asr переписываются без изменений.
Элементы разрешающей
строки за исключением asr изменяют знак на противоположный.
Оставшиеся элементы новой
симплекс-таблицы вычисляются согласно следующему правилу: произведение
соответствующего элемента прежней таблицы на разрешающий элемент asr минус произведение
элементов, находящихся на другой диагонали таблицы. В соответствии с этим
правилом имеем:
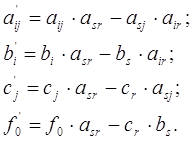
Все элементы полученной
таблицы необходимо разделить на разрешающий элемент asr:
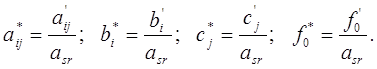
Таблица 3. Итерация №1
| БП |
СЧ |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
X10 |
| X6 |
825/2 |
0 |
15/4 |
5/4 |
3/4 |
5/2 |
1 |
0 |
-1/4 |
0 |
0 |
| X7 |
215 |
0 |
3/2 |
-1/2 |
7/2 |
1 |
0 |
1 |
-1/2 |
0 |
0 |
| X1 |
375/2 |
1 |
1/4 |
3/4 |
1/4 |
1/2 |
0 |
0 |
1/4 |
0 |
0 |
| X9 |
215/2 |
0 |
5/4 |
7/4 |
5/4 |
-1/2 |
0 |
0 |
-3/4 |
1 |
0 |
| X10 |
615/2 |
0 |
7/4 |
1/4 |
15/4 |
7/2 |
0 |
0 |
-1/4 |
0 |
1 |
| Y |
11250 |
0 |
-35 |
8 |
-30 |
-26 |
0 |
0 |
15 |
0 |
0 |
XБ1=(x6, x7, x1, x9, x10)T.
Базис XБ1=(x6, x7, x1, x9,
x10)T является допустимым, но не оптимальным. Разрешающий элемент таблицы a92=5/4
определяет необходимость перехода к базису XБ2=(x6, x7, x1, x2, x10)T. Приведем
результат пересчета симплекс-таблицы для базиса XБ2.
Таблица 4. Итерация №2.
| БП |
СЧ |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
X10 |
| X6 |
90 |
0 |
0 |
-4 |
-3 |
4 |
1 |
0 |
2 |
-3 |
0 |
| X7 |
86 |
0 |
0 |
-13/5 |
2 |
8/5 |
0 |
1 |
2/5 |
-6/5 |
0 |
| X1 |
166 |
1 |
0 |
2/5 |
0 |
3/5 |
0 |
0 |
2/5 |
-1/5 |
0 |
| X2 |
86 |
0 |
1 |
7/5 |
1 |
-2/5 |
0 |
0 |
-3/5 |
4/5 |
0 |
| X10 |
157 |
0 |
0 |
-11/5 |
2 |
21/5 |
0 |
0 |
4/5 |
-7/5 |
1 |
| Y |
14260 |
0 |
0 |
57 |
5 |
-40 |
0 |
0 |
-6 |
28 |
0 |
Базис XБ2=(x6, x7, x1, x2,
x10)T является допустимым, но не оптимальным. Разрешающий элемент таблицы a65=4
определяет необходимость перехода к базису XБ3=( x5, x7, x1, x2, x10)T.
Приведем результат пересчета симплекс-таблицы для базиса XБ3.
Таблица 5. Итерация №3
| БП |
СЧ |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
X10 |
| X5 |
45/2 |
0 |
0 |
-1 |
-3/4 |
1 |
1/4 |
0 |
1/2 |
-3/4 |
0 |
| X7 |
50 |
0 |
0 |
-1 |
16/5 |
0 |
-2/5 |
1 |
-2/5 |
0 |
0 |
| X1 |
305/2 |
1 |
0 |
1 |
9/20 |
0 |
-3/20 |
0 |
1/10 |
1/4 |
0 |
| X2 |
95 |
0 |
1 |
1 |
7/10 |
0 |
1/10 |
0 |
-2/5 |
1/2 |
0 |
| X10 |
125/2 |
0 |
0 |
2 |
103/20 |
0 |
-21/20 |
0 |
-13/10 |
7/4 |
1 |
| Y |
15160 |
0 |
0 |
17 |
-25 |
0 |
10 |
0 |
14 |
-2 |
0 |
Базис XБ3=(x5, x7, x1, x2,
x10)T является допустимым, но не оптимальным. Разрешающий элемент таблицы
a104=103/20 определяет необходимость перехода к базису XБ4=(x5, x7, x1, x2,
x4)T. Приведем результат пересчета симплекс-таблицы для базиса XБ4.
Таблица 6. Итерация №4
| БП |
СЧ |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
X10 |
| X5 |
3255/103 |
0 |
0 |
-73/103 |
0 |
1 |
10/103 |
0 |
32/103 |
-51/103 |
15/103 |
| X7 |
1150/103 |
0 |
0 |
-231/103 |
0 |
0 |
26/103 |
1 |
42/103 |
-112/103 |
-64/103 |
| X1 |
15145/103 |
1 |
0 |
85/103 |
0 |
0 |
-6/103 |
0 |
22/103 |
10/103 |
-9/103 |
| X2 |
8910/103 |
0 |
1 |
75/103 |
0 |
0 |
25/103 |
0 |
-23/103 |
27/103 |
-14/103 |
| X4 |
1250/103 |
0 |
0 |
40/103 |
1 |
0 |
-21/103 |
0 |
-26/103 |
35/103 |
20/103 |
| Y |
15463,4 |
0 |
0 |
2751/103 |
0 |
0 |
505/103 |
0 |
792/103 |
669/103 |
500/103 |
Анализ Таблицы 6 позволяет
сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T.
3.4
Результат решения задачи планирования производства
В результате решения
поставленной задачи симплекс-методом получили набор производимой продукции
x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который
удовлетворяет всем наложенным ограничениям и обеспечивает максимальную
стоимость данного набора (максимум целевой функции f(x)=
60x1+50x2+37x3+45x4+56x5=15463,4 рублей). Таким образом, можно оптимально
спланировать объем производства продукции при наличии заданного количества
ресурсов: продукции типа A нужно выпустить 147 единиц, продукции типа B – 86
единиц, продукции типа D – 12 единиц, продукции типа E – 31 единицу, а
продукцию типа D – для достижения максимальной прибыли в данных условиях
производить не выгодно.
При этом ресурсы типа 1,
3, 4, 5 будут использованы полностью, а 11 единиц ресурса типа 2 останутся
неизрасходованными.
4.
Программа для решения задач ЛП симплекс методом
4.1
Описание
В процессе выполнения
дипломной работы был реализован и отлажен программный интерфейс под ОС Windows
XP (также протестирован под Windows Vista), решающий задачи ЛП симплекс методом
(в частности поставленную задачу планирования производства).
Программа осуществляет: решение
задач ЛП симплекс методом; сохранение и загрузка исходных данных в файл/из
файла; вывод решения по шагам; экспорт решения в документ MS word; системный
код программы написан в среде объектно-ориентированного программирования С++.
4.2
Графическое представление программы
Главное окно программы
«Исходные данные»:
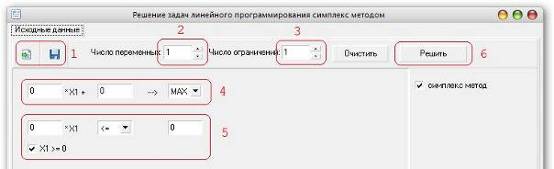
Рис.5 Главное окно
программы Simplex: 1 – Кнопки загрузка/сохранение исходных данных в файл. 2 –
Число переменных, в нашем случае количество производимой продукции. 3 – Число
ограничений, в нашем случае количество запасов ресурсов на складе. 4 – Целевая
функция, в нашем случае максимизация. 5 – Система ограничений в форме Такера. 6
– Кнопка для решения задачи и перехода к окну «Решение».
Окно программы «Решение»:
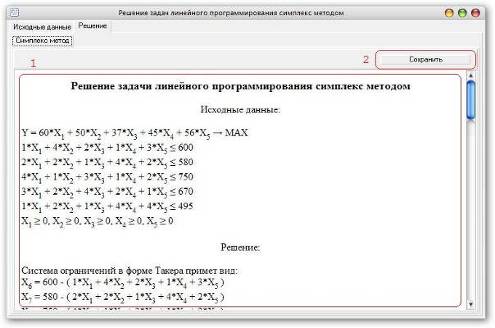
Рис.6 Окно программы
Simplex, для просмотра решения по шагам: 1 – Поле для вывода пошагового решения
задачи. 2 – Кнопка для экспорта результатов работы программы в документ MS
Word.
4.3
Работа с программой
1 – Определяем число
переменных; 2 – Определяем максимизируем или минимизируем целевую функцию; (см.
Рис.7)
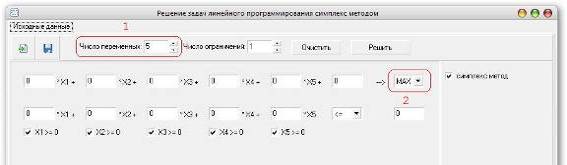
Рис.7 Работа с программой
3 – Определяем число
ограничений; 4 – Определяем знаки неравенств для системы ограничений; 5 –
Указываем дополнительные ограничения неотрицательности; (см. Рис.8)
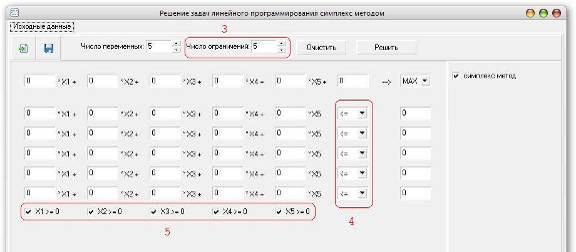
Рис.8 Работа с программой
Приступаем к вводу
исходных данных: 6 – поля для ввода коэффициентов целевой функции (в нашем
случае это цена единицы продукции типа A,…,E); 7 – поля для ввода запасов
каждого ресурса; 8 – поля для ввода набора производимой продукции. Заполнив все
поля, приступаем к решению задачи: 9 – нажимаем кнопку «Решить». (см. Рис.9)
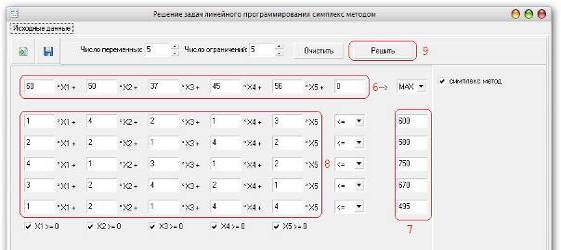
Рис.9 Работа с программой
После нажатия кнопки «Решения»
программа производит необходимые вычисления и автоматически переходит ко
второму окну, в котором отображается пошаговое решение поставленной задачи в
виде симплекс таблиц, с указанием необходимых дополнительных данных. А именно: 10
- исходные данные; 11 - система ограничений в форме Такера; 12 - целевая
функция; 13 – исходная симплекс таблица; (см. Рис.10)
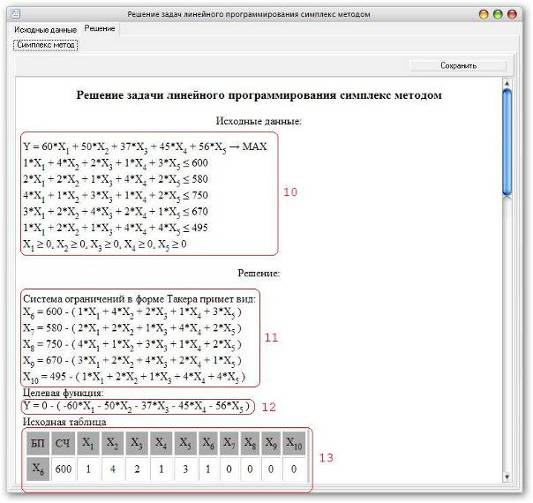
Рис.10 Работа с программой
14 - разрешающий элемент
каждой таблицы, 15 - переход от старого базиса к новому, 16 - количество
итераций, 17 - информация об оптимальности решения, 18 – Ответ, в нашем случае
максимум целевой функции (максимальная прибыль), 19 – оптимальный набор
производимой продукции (количество изделий A,…,E). (см. Рис.11)
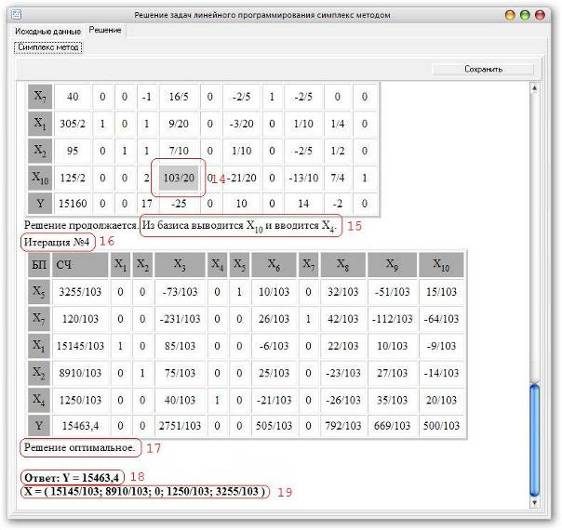
Рис.11 Работа с программой
4.4
Схема программы
Логическая структура
программы решающей задачи ЛП симплекс методом приведена на Рис.12, Рис.13,
Рис.14.
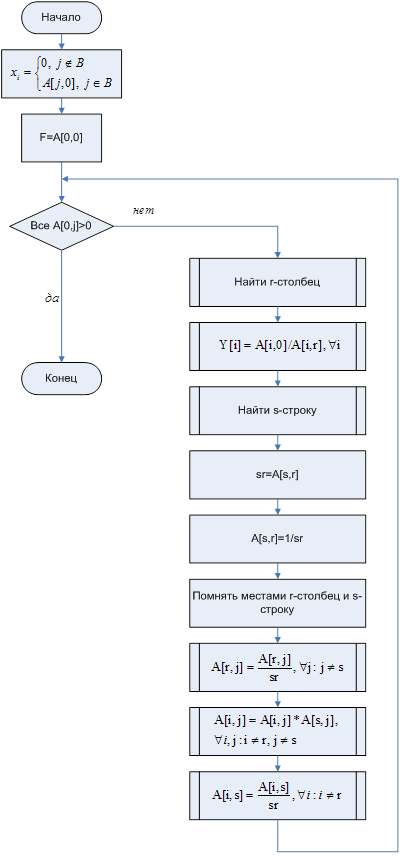
Рис.12 Симплекс метод
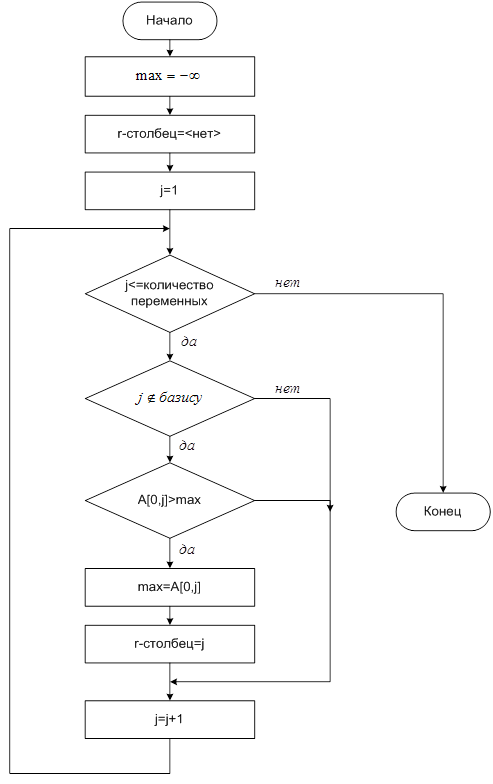
Рис.13 Поиск r-столбца
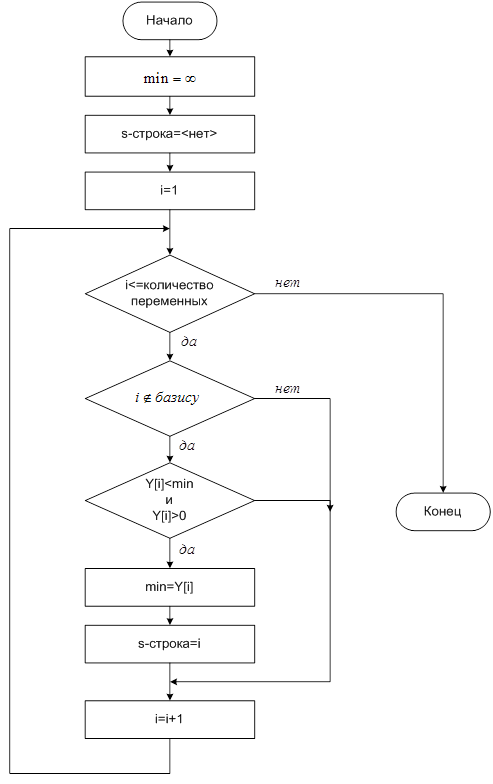
Рис.14 Поиск s-строки
Заключение
Развитие современного
общества характеризуется повышением технического уровня, усложнением
организационной структуры производства, углублением общественного разделения
труда, предъявлением высоких требований к методам планирования производственной
деятельности. В этих условиях только научный подход к экономике предприятий
позволит обеспечить высокие темпы развития промышленности. Научного подхода
требует и решение тактических и стратегических задач.
В настоящее время новейшие
достижения математики и современной вычислительной техники находят все более
широкое применение как в экономических исследованиях и планировании, так и в
других задачах. Этому способствует развитие таких разделов математики как
математическое программирование, теория игр, теория массового обслуживания, а
также бурное развитие быстродействующей электронно-вычислительной техники.
Уже накоплен большой опыт
постановки и решения экономических и тактических задач с помощью математических
методов. Особенно успешно развиваются методы оптимального управления. Экономика
и производство развивается быстро там, где широко используются математические
методы.
Список
литературы
1.
Схрейвер А. Теория линейного и целочисленного программирования: в 2-х т.
Т.2: Пер с англ. - М.: Мир, 1991. - 342с., ил. Раздел Целочисленное линейное
программирование
2.
Конюховский П.В. Математические методы исследования операций в
экономике. - СПб: Питер, 2002. - 208 с.: ил. - (Серия "Краткий
курс"). Раздел 4.2 Метод Гомори
3.
Хемди А. Таха Глава 3. Симплекс-метод // Введение в исследование операций
= Operations Research: An Introduction. — 7-е изд. — М.: «Вильямс», 2007. — С.
95-141. — ISBN 0-13-032374-8
4.
Томас Х. Кормен и др. Глава 29. Линейное программирование // Алгоритмы:
построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс»,
2006. — С. 1296. — ISBN 0-07-013151-1
5.
Ершов А.Т., Карандаев И.С., Шананин Н.А. Планирование производства и
линейное программирование. МИУ, М., 1981.
6.
Акулич И.Л., «Математическое программирование в примерах и задачах»,
Москва «Высшая школа» 1993г.
7.
Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. «Математическое
программирование», Москва «Высшая школа» 1980г.
8.
Вентцель Е.С. Исследование операций: задачи, принципы, методологии. М.:
Изд-во «Наука», 1980.
9.
Джерод Холлингворс, Дэн Баттерфилд, Боб Свот C++ Builder 5. Руководство
разработчика = C++ Builder 5 Developer's Guide. — М.: «Диалектика», 2001. — С.
884. — ISBN 0-672-31972-1
10.
Джаррод Холингворт, Боб Сворт, Марк Кэшмэн, Поль Густавсон
Borland C++ Builder 6. Руководство разработчика = Borland C++
Builder 6 Developer's Guide. — М.: «Вильямс», 2004. — С. 976. — ISBN 0-672-32480-6
11.
Леоненков А.В. Решение задач оптимизации в среде MS Excel
BHV-Санкт-Петербург ISBN: 5941575033 2005 г.
Приложение 1
Листинг программы
// Этот файл определяет
класс симплекс метода
#include
<vcl.h>
#include
<list>
#include
"CD.cpp"
#ifndef
CSM2_H
#define
CSM2_H
namespace
SM
{
//----------------Симплекс
метод------------------------------
class CSM
{
public:
CSM( int
n, int m );
void
SetBaz( int * baz );
int SetT(
CD ** T );
void
Show();
AnsiString
GetWord();
AnsiString
GetTacker();
AnsiString
Get_Rap();
int
operator<<=( CSM * csm );
CD
get_CF();
CD**
get_ogr(){ return T; }
int*
get_baz(){ return baz; }
int
get_rez(){ return rez; }
void
get_nm( int* nIn, int* mIn ){ *nIn = n; *mIn = m; }
void
get_ij( int* i, int* j ){ *i = a_i; *j = a_j; }
~CSM( );
private:
static int
iter; // Число итераций
int optim(); // проверка
решение (0 - оптимальное, 1 - не существует, 2 - не оптимальное)
int n; // Число переменных
int m; // Число
ограничений
int a_i;
int a_j; // Координаты
разрешающего элемента
int * baz; // Массив
базисных переменных
CD ** T; // Симплекс
таблица
int rez;
};
int CSM::iter = 0; //
Число итераций
CSM::CSM(
int nIn, int mIn )
{
n = nIn;
m = mIn;
baz = new
int [m];
T = new CD * [m + 1]; // m
+ 1 т.к. еще строка целевой функции
for( int
i = 0; i < m + 1; i++ )
T[i] = new CD [n + 1]; //
n + 1 т.к. еще свободный член
iter +=
1;
rez = 2;
}
CSM::~CSM(
)
{
delete
baz;
for( int
i = 0; i < m + 1; i++ )
delete
T[i];
delete T;
iter -=
1;
}
void
CSM::SetBaz( int * bazIn )
{
for( int
i = 0; i < m; i++ )
baz[i] = bazIn[i];
}
int CSM::SetT( CD ** TIn )
// Копирование входящей таблицы и проверка решения с поиском разрешающего
элемента
{
for( int
i = 0; i < m + 1; i++ )
for( int
j = 0; j < n + 1; j++ )
T[i][j] =
TIn[i][j];
return
optim();
}
int CSM::optim()
{
a_i = a_j = 0; //
Инициализация координат разрешающего элемента
// Проверка на
отрицательность среди свободных членов
for( int i = 1; i < m;
i++ ) // проверка свободного члена
if(
T[i][0].get_d() < T[a_i][0].get_d() ) // Ищем минимальный
a_i = i;
if( T[a_i][0].get_d() <
0 ) // Если минимальный элемент отрицательный (двойственный СМ)
{
for( int j = 1; j < n +
1; j++ ) // проверка на наличие отрицательных эл-тов в строке
if( T[a_i][j].get_d() <
0 ) // есть отрицательные элементы
{
a_j = j; // Первый
отрицательный элемент
break; // Выход из цикла
поиска
}
if( a_j == 0 ) return rez
= 1; // Нет оптимального решения // выход
for( int j = a_j + 1; j
< n + 1; j++ ) // Проходим по строке еще раз для нахождения минимального
отношения
if(
T[a_i][j].get_d() < 0 ) // Отрицательный
if( fabs(
(T[m][j]/T[a_i][j]).get_d() ) < fabs( (T[m][a_j]/T[a_i][a_j]).get_d() ) ) //
Наименьшее отношение
a_j = j;
return rez = 2; //
продолжение выполнений итераций // выход
}
// Проверка на
отрицательность среди элементов целевой функции
a_j = 1;
a_i = m;
for( int j = 2; j < n +
1; j++ ) // Проходим по строке целевой функции
if(
T[m][j].get_d() < T[m][a_j].get_d() ) // Ищем минимальный
a_j = j;
if( T[m][a_j].get_d() <
0 ) // Есть отрицательный элемент в целевой функции
{
for( int
i = 0; i < m; i++ ) // Проходим по столбцу
if(
T[i][a_j].get_d() > 0 )
{
a_i = i; // Первый
положительный элемент
break; // Выход из цикла
поиска
}
if( a_i == m ) return rez
= 1; // Нет оптимального решения // выход
for( int i = a_i + 1; i
< m; i++ ) // Проходим по столбцу еще раз для нахождения минимального
отношения
if(
T[i][a_j].get_d() > 0 ) // Положительный
if( fabs(
(T[i][0]/T[i][a_j]).get_d() ) < fabs( (T[a_i][0]/T[a_i][a_j]).get_d() ) ) //
Наименьшее отношение
a_i = i;
return rez = 2; //
продолжение выполнений итераций // выход
}
return rez = 0; //
оптимальное решение // выход
}
int
CSM::operator<<=( CSM * csmIn ) // Здесь из предыдущей таблицы получается
новая
{
a_i =
csmIn->a_i;
a_j =
csmIn->a_j;
// Делим на разрешающий
элемент разрешающую строку и меняем базисную переменную
for( int
j = 0; j < n + 1; j++ )
T[a_i][j]
= csmIn->T[a_i][j] / csmIn->T[a_i][a_j];
// Домножаем разрешающую
строку на эл-т в разрешающем столбце, соотв-щий данной строке, и складываем с
данной строкой
for( int
i = 0; i < m + 1; i++)
{
if( i ==
a_i) continue;
for( int
j = 0; j < n + 1; j++ )
T[i][j] =
csmIn->T[i][j] - T[a_i][j] * csmIn->T[i][a_j];
}
// Вводим новую переменную
в базис
for( int i = 0; i < m;
i++ )
baz[i] =
csmIn->baz[i];
baz[a_i]
= a_j;
return
optim();
}
CD
CSM::get_CF()
{
return
T[m][0];
}
void
CSM::Show( )
{
AnsiString
tab;
tab =
"БП\tСЧ";
for( int
j = 0; j < n; j++)// шапка
tab = tab
+ "\tX" + AnsiString( j + 1 );
for( int
i = 0; i < m + 1; i++ )
{
if( i ==
m ) tab = tab + "\nY";
else tab
= tab + "\n" + baz[i];
for( int
j = 0; j < n + 1; j++)
tab = tab
+ "\t" + T[i][j].get_a();
}
// ShowMessage(tab);
}
AnsiString
CSM::GetWord()
{
// Таблица
AnsiString
tab;
tab =
"\n<table border=3 cellpadding=5 ><tr
bgcolor=\"#aaaaaa\">";
tab +=
"<td align=\"center\">БП</td><td>СЧ</td>";
for( int
j = 0; j < n; j++)// шапка
{
tab +=
"<td align=\"center\">";
tab = tab
+ "X<sub>" + (j+1) + "</sub>";
tab +=
"</td>";
}
tab +=
"</tr>";
for( int
i = 0; i < m + 1; i++ )
{
tab +=
"<tr>";
tab +=
"<td bgcolor=\"#aaaaaa\"
align=\"center\">";
if( i ==
m ) tab += "F'";
else tab
= tab + "X<sub>" + baz[i] + "</sub>";
tab +=
"</td>";
for( int
j = 0; j < n + 1; j++)
{
if( i ==
a_i && j == a_j && rez == 2 ) tab += "<td
bgcolor=\"#cccccc\">";
else tab
+= "<td align=\"center\">";
tab +=
T[i][j].get_a();
tab +=
"</td>";
}
tab +=
"</tr>";
}
tab +=
"</table>";
return
tab;
/*
AnsiString
tab;
tab =
"БП;СЧ;";
for( int
j = 0; j < n; j++)// шапка
if( j ==
n - 1 ) tab = tab + "X" + AnsiString( j + 1 );
else tab
= tab + "X" + AnsiString( j + 1 ) + ";";
for( int
i = 0; i < m + 1; i++ )
{
if( i ==
m ) tab = tab + "\nF';";
else tab
= tab + "\nX" + baz[i] + ";";
for( int
j = 0; j < n + 1; j++)
if( j ==
n ) tab = tab + T[i][j].get_a();
else tab
= tab + T[i][j].get_a() + ";";
}
return
tab;
*/
}
AnsiString
CSM::GetTacker()
{
AnsiString
tab;
for( int
i = 0; i < m; i++ )
{
tab +=
AnsiString("X") + baz[i] + " = ";
tab +=
T[i][0].get_a() + " - ( " + T[i][1].get_a() + "*X1";
for( int
j = 2; j < n + 1; j++)
{
bool is_b
= false;
for( int
d = 0; d < m; d++ )
if( j ==
baz[d] )
{
is_b =
true;
break;
}
if( !is_b
)
tab +=
T[i][j].get_s() + "*X" + AnsiString( j );
}
tab +=
" )\n";
}
tab +=
"\nЦелевая функция:";
tab +=
"\nF' = " + T[m][0].get_a() + " - ( " + T[m][1].get_a() +
"*X1";
for( int
j = 2; j < n + 1; j++)
{
bool is_b
= false;
for( int
d = 0; d < m; d++ )
if( j ==
baz[d] )
{
is_b =
true;
break;
}
if( !is_b
)
tab +=
T[m][j].get_s() + "*X" + AnsiString( j );
}
tab +=
" )\n";
return
tab;
}
AnsiString
CSM::Get_Rap()
{
AnsiString
Rap;
if( rez
== 0 )
{
if(
T[m][0] == 0 )
Rap = "Решение
оптимальное. Искусственный базис получен. Далее подставляем новые бвазисные
пременные в целевую функцию.";
else Rap = "Решение
оптимальное, но целевая функция не равна 0. искусственного базиса нет.";
}
else if(
rez == 1 )
{
if( a_j
== 0 ) Rap = AnsiString( "Решения не существует. Целевая
функция неограничена, т.к. свободный член при X" ) + baz[a_i] + "
отрицательный, а другие элементы строки не отрицательные.";
else if(
a_i == m ) Rap = AnsiString( "Решения не существует. Целевая функция неограничена, т.к. элемент в строке целевой
функции при X" ) + a_j + " отрицательный, а другие элементы столбца
не положительные.";
}
else if(
rez == 2 )
{
Rap =
AnsiString( "Решение продолжается. Из
базиса выводится X") + baz[a_i] + " и вводится X" + a_j +
".";
}
return Rap;
}
}
#endif // CSM_H
// Этот файл определяет
класс дроби
#include
<vcl.h>
#include
<math.h>
#ifndef
CD_H
#define
CD_H
#define
PR_COUNT 5000
int
mas[PR_COUNT] = {0};
void
Generate_Prost();
class CD
// Класс дробь
{
public:
CD::CD(
int = 0, int = 1 );
bool Set(
int hi, int lo );
bool Set(
double d );
bool Set(
AnsiString d );
bool
SetInv( AnsiString d );
int hi(){
return m_hi; }; // числитель
int lo(){
return m_lo; }; // знаменатель
double get_d(); //
возвращает десятичное значение
AnsiString get_a(); //
возвращает строку обычной дроби
AnsiString get_s(); //
возвращает строку обычной дроби
CD
get_dr();
int
get_cel();
CD
get_abs();
CD
operator*(CD d);
CD
operator*(int num);
CD
operator/(CD d);
CD
operator/(int num);
CD
operator+(CD d);
CD
operator+(int num);
CD
operator-(CD d);
CD
operator-(int num);
CD
operator=(CD d);
CD
operator=(int num);
bool
operator==(CD d);
bool
operator==(int num);
bool
operator!=(CD d);
bool
operator!=(int num);
private:
int m_hi; // числитель
int m_lo; // знаменатель
double
m_d;
bool
overflow;
void
optim();
static
bool gen;
};
bool
CD::gen = false;
CD::CD(
int hi, int lo )
{
if( !gen
)
{
Generate_Prost();
gen =
true;
}
overflow
= false;
Set( hi,
lo );
}
bool
CD::Set( int hi, int lo )
{
overflow
= false;
if( lo ==
0 )
{
m_hi = 0;
m_lo = 1;
return
false;
}
m_hi =
hi;
if( m_hi
== 0 ) m_lo = 1;
else
{
m_lo =
lo;
optim();
}
return
true;
}
bool
CD::Set( double d )
{
overflow
= true;
m_d = d;
return
true;
}
bool
CD::Set( AnsiString d )
{
int pos =
0;
if( pos =
d.LastDelimiter("/") )
{
m_hi =
StrToIntDef( d.SubString( 1, pos - 1 ), 0 );
m_lo =
StrToIntDef( d.SubString( pos + 1, d.Length() ), 1 );
Set(
m_hi, m_lo );
}
else if(
pos = d.LastDelimiter(".,") )
{
Set(
StrToFloat( d ) );
}
else
{
m_hi =
StrToIntDef( d, 0 );
Set(
m_hi, 1 );
}
optim();
// ShowMessage(
"m_hi = " + AnsiString(m_hi) + "\nm_lo = " + m_lo );
return
true;
}
bool
CD::SetInv( AnsiString d )
{
int pos =
0;
if( pos =
d.LastDelimiter("/") )
{
m_hi =
-StrToIntDef( d.SubString( 1, pos - 1 ), 0 );
m_lo =
StrToIntDef( d.SubString( pos + 1, d.Length() ), 1 );
Set(
m_hi, m_lo );
}
else if(
pos = d.LastDelimiter(".,") )
{
Set(
-StrToFloat( d ) );
}
else
{
m_hi =
-StrToIntDef( d, 0 );
Set(
m_hi, 1 );
}
// ShowMessage(
"m_hi = " + AnsiString(m_hi) + "\nm_lo = " + m_lo );
return true;
}
double CD::get_d() //
возвращает десятичное значение
{
if(
overflow ) return m_d;
if ( m_hi
) return float(m_hi)/m_lo;
else
return 0;
}
AnsiString
CD::get_a()
{
if(
overflow ) return FloatToStrF( m_d, ffGeneral, 7, 0 );
if ( m_lo
== 1 ) return AnsiString(m_hi);
else
return AnsiString(m_hi) + "/" + AnsiString(m_lo);
}
AnsiString
CD::get_s()
{
if(
overflow )
{
if( m_d
>= 0 ) return AnsiString( " + " ) + FloatToStrF( m_d, ffGeneral,
7, 0 );
else
return AnsiString( " - " ) + FloatToStrF( -m_d, ffGeneral, 7, 0 );
}
if ( m_lo
== 1 ) return (m_hi < 0)?AnsiString(" - ") + abs(m_hi):" +
" + AnsiString(m_hi);
else
return ((m_hi < 0)?AnsiString(" - ") + abs(m_hi):" + " +
AnsiString(m_hi)) + "/" + AnsiString(m_lo);
}
CD
CD::get_dr()
{
CD cd;
if(
overflow )
{
cd.Set(
m_d - floor(m_d) );
return
cd;
}
ldiv_t r;
r = ldiv(
m_hi, m_lo );
if( r.rem
>= 0 )
{
cd.Set(
r.rem, m_lo );
}
else
{
cd.Set(
m_lo + r.rem, m_lo );
}
return
cd;
}
int
CD::get_cel()
{
int cd;
if(
overflow )
{
cd =
floor( m_d );
return
cd;
}
if( m_hi
>= 0 )
cd =
ldiv( m_hi, m_lo ).quot;
else
cd =
ldiv( m_hi, m_lo ).quot - 1;
return
cd;
}
CD
CD::get_abs()
{
CD cd;
if(
overflow )
{
if( m_d
>= 0 ) cd.Set( m_d );
else
cd.Set( -m_d );
return
cd;
}
if( m_hi
< 0 ) cd.Set( -m_hi, m_lo );
else
cd.Set( m_hi, m_lo );
return
cd;
}
CD
CD::operator+(CD d)
{
CD cd;
if(
overflow || d.overflow )
{
cd.Set(
get_d() + d.get_d() );
return
cd;
}
cd.Set(
m_hi*d.m_lo + d.m_hi*m_lo, m_lo*d.m_lo );
return
cd;
}
CD
CD::operator+(int num)
{
CD cd;
if(
overflow )
{
cd.Set(
get_d() + num );
return
cd;
}
cd.Set(
m_hi + num*m_lo, m_lo );
return
cd;
}
CD
CD::operator-(CD d)
{
CD cd;
if(
overflow || d.overflow )
{
cd.Set(
get_d() - d.get_d() );
return
cd;
}
cd.Set(m_hi*d.m_lo
- d.m_hi*m_lo, m_lo*d.m_lo );
return
cd;
}
CD
CD::operator-(int num)
{
CD cd;
if(
overflow )
{
cd.Set(
get_d() - num );
return
cd;
}
cd.Set(
m_hi - num*m_lo, m_lo );
return
cd;
}
CD
CD::operator*(CD d)
{
CD cd;
if(
overflow || d.overflow )
{
cd.Set(
get_d() * d.get_d() );
return
cd;
}
cd.Set(
m_hi*d.m_hi, m_lo*d.m_lo );
return
cd;
}
CD
CD::operator*(int num)
{
CD cd;
if(
overflow )
{
cd.Set(
get_d() * num );
return
cd;
}
cd.Set(
m_hi*num, m_lo );
return
cd;
}
CD
CD::operator/(CD d)
{
CD cd;
if(
overflow || d.overflow )
{
cd.Set(
get_d() / d.get_d() );
return
cd;
}
cd.Set(
m_hi*d.m_lo, m_lo*d.m_hi );
return
cd;
}
CD
CD::operator/(int num)
{
CD cd;
if( overflow
)
{
cd.Set(
get_d() / num );
return
cd;
}
cd.Set(
m_hi, m_lo*num );
return
cd;
}
CD
CD::operator=(CD d)
{
if(
d.overflow)
{
Set(
d.get_d() );
return
*this;
}
Set(
d.m_hi, d.m_lo );
return
*this;
}
CD
CD::operator=(int num)
{
Set( num,
1 );
return
*this;
}
bool
CD::operator==(CD d)
{
if(
overflow || d.overflow )
{
return
get_d() == d.get_d();
}
if( m_hi
== d.m_hi )
if( m_lo
== d.m_lo )
return
true;
return
false;
}
bool
CD::operator==(int num)
{
if(
overflow )
{
return
get_d() == num;
}
if( m_hi
== num )
if( m_lo
== 1 )
return
true;
return
false;
}
bool
CD::operator!=(CD d)
{
if(
overflow || d.overflow )
{
return
get_d() != d.get_d();
}
if( m_hi
== d.m_hi )
if( m_lo
== d.m_lo )
return
false;
return
true;
}
bool
CD::operator!=(int num)
{
if(
overflow )
{
return
get_d() != num;
}
if( m_hi
== num )
if( m_lo
== 1 )
return
false;
return
true;
}
void
CD::optim()
{
if(
overflow ) return;
m_hi *=
m_lo/abs(m_lo); // для знака
m_lo = abs(m_lo);
if( m_hi ) // далее
сокращение дроби
{
int i =
0;
while(1)
{
while(
ldiv( m_hi, mas[i] ).rem == 0 && ldiv( m_lo, mas[i] ).rem == 0 )
{
m_hi /=
mas[i];
m_lo /=
mas[i];
}
if(
(mas[i + 1] > abs(m_hi) && mas[i + 1] > m_lo) || i + 1 >
PR_COUNT - 1 ) break;
i++;
}
if(
abs(m_hi) > mas[PR_COUNT - 1] || m_lo > mas[PR_COUNT - 1] )
{
overflow
= true;
m_d =
double(m_hi)/m_lo;
return;
}
}
}
void
Generate_Prost()
{
bool
is_prost;
float
per;
int kol =
1;
mas[0] =
2;
int i =
3;
while(1)
{
is_prost
= true;
for( int
j = 0; j < kol; j++ )
if( ldiv(
i, mas[j] ).rem == 0 )
{
is_prost
= false;
break;
}
if(
is_prost )
{
mas[kol]
= i;
kol++;
}
if( kol
>= PR_COUNT ) return;
i++;
}
/*
AnsiString
p;
for( int
i = 0; i < kol; i++ )
p = p +
mas[i] + " ";
// ShowMessage(
p );
//*/
}
#endif // CD_H
Приложение 2
Леонид Витальевич
Канторович

Рис. 15 Портрет Л.В.
Канторович
Леонид Витальевич
Канторович вошел в плеяду крупнейших ученых двадцатого века благодаря своему
капитальному вкладу в математику и экономику. Исследования Л.В. Канторовича в области
функционального анализа, вычислительной математики, теории экстремальных задач,
дескриптивной теории функций и теории множеств оказали влияние на становление и
развитие указанных математических дисциплин, послужили основой для формирования
новых научных направлений.
Л.В. Канторович по праву
считается одним из основоположников современного экономико-математического
направления, ядро которого составляют теория и модели линейных экстремальных
задач. Это направление было затем переоткрыто и развито в трудах других ученых
(прежде всего Дж. Данцига) и получило название линейное программирование. Идеи
и методы этой дисциплины широко используются для постановки и решения
разнообразных экстремальных и вариационных задач не только в экономике, но и в
физике, химии, энергетике, геологии, биологии, механике и теории управления.
Линейное программирование оказывает существенное влияние также на развитие
вычислительной математики и вычислительной техники. Нам представляется, что
никто другой не сделал так много для использования линейного программирования в
экономической теории, как Л. В. Канторович.
В настоящее время
многочисленные ученики и последователи Л. В. Канторовича успешно работают в различных
областях современной математики и экономики, добиваясь значительных научных
результатов. Выдающиеся заслуги Л. В. Канторовича были отмечены государством.
Он награжден двумя орденами Ленина — в те годы наивысшими наградами страны,
тремя орденами Трудового Красного Знамени, орденами «Знак Почета» и Отечественной
войны II степени, многими медалями.
Л.В. Канторович являлся
членом ряда зарубежных академий и почетным доктором многих университетов,
участвовал в работе международных научных обществ. С момента основания
«Сибирского математического журнала» до своей кончины Леонид Витальевич
Канторович входил в состав редколлегии, определяя научное лицо журнала в области
прикладного функционального анализа и математической экономики.
До последних своих дней
Леонид Витальевич был полон творческих планов и активно работал над их
претворением в жизнь. Уже в последние месяцы своей жизни, находясь в больнице,
он продиктовал свои автобиографические заметки «Мой путь в науке»,
опубликованные в «Успехах математических наук», и работал над статьей
«Функциональный анализ (основные идеи)», опубликованной в СМЖ в 1987 г.
Леонид Витальевич всегда
мечтал о внедрении новых математических методов в хозяйственную практику своей
Родины и служил этой мечте до своей кончины 7 апреля 1986 г., невзирая на непонимание
и откровенное противодействие ретроградов от науки и политики, управлявших
страной. Л. В. Канторович похоронен в Москве на Новодевичьем кладбище. Эти
факты имеет смысл напомнить еще и потому, что после смерти Л. В. Канторовича в «Новом
мире» (№ 12 за 1996 г.) были опубликованы выдумки о борьбе Л. В. Канторовича с идеей
планирования в экономике и якобы имевшей место эмиграции в Америку еще в 70-е гг.
Клевета настигла его и после смерти …
Научная школа Л. В.
Канторовича, будь то в математике или в экономике, — это не только десятки
непосредственных его учеников. Это и огромное число последователей, для которых
работы Л. В. Канторовича и общение с ним определили характер научного мышления
и деятельности на всю жизнь.
Для своих учеников и последователей
Леонид Витальевич всегда был образцом честности, бескомпромиссности и твердости
в науке, объективности и трудолюбия. Подкупающими чертами его личности были
исключительная доброта, простота и легкость в общении, скромность и даже
застенчивость. Он всегда с удовольствием работал с молодежью, и молодежь
тянулась к нему.
Леонид Витальевич Канторович
указал нам один из путей в будущее. Мы не сомневаемся, что этот путь выберут
многие.
|