Дипломная работа: Классификация римских цифр на основе нейронных сетей
Дипломная работа: Классификация римских цифр на основе нейронных сетей
ЗАДАНИЕ
на курсовое проектирование
Тема курсового проекта
Классификация римских
цифр на основе нейронных сетей
Исходные данные к проекту
1.
NeuroShell2
русское издание
2.
NeuroShell
Classifier v2.0
3.
NeuroPro
Содержание пояснительной записки
1.
Назначение
проекта
2.
Требования
3.
Выбор
нейронной сети и нейропакета
4.
Обучение
5.
Блок-схема
алгоритма обучения
6.
Тестовый
пример
Рекомендуемая литература
1.
Стандарт
предприятия СТП 1–У–НГТУ–98
2.
Круглов В.В.,
Борисов В.В. Искусственные нейронные сети. Теория и практика. – М.: Горячая
линия – Телеком, 2001. – 382 с.:ил.
3.
Электронный
учебник по NeuroShell 2
4.
Каллан Р. Основные концепции нейронных сетей
Содержание
1
Анализ исходных
данных и разработка ТЗ
1.1
Основание и
назначение разработки
1.2
Классификация
решаемой задачи
1.3
Предварительный
выбор класса нейронной сети
1.4
Предварительный
выбор структуры нейронной сети
1.5
Выбор пакета
нейронной сети
1.6
Минимальные
требования к информационной и программной совместимости
1.7
Минимальные
требования к составу и параметрам технических средств
2
Обучение
нейронной сети
2.1
Формирование
исходных данных
2.2
Окончательный
выбор модели, структуры нейронной сети
2.3
Выбор параметров
обучения
2.4
Оптимальные
параметры обучения
2.5
Блок-схема
алгоритма обучения
3
Анализ качества
обучения
Вывод
Список использованных источников
1. Анализ исходных
данных и разработка технического задания
1.1 Основание и
назначение разработки
Данную разработку
технического задания можно отнести к применению нейронных сетей, выполняется
как курсовая работа в пределах дисциплины «Представление знаний в информационных
системах». Целью данной разработки является освоение моделирования нейронных
сетей. Назначением работы является необходимость решения задачи классификация
римских цифр на основе нейронной сети.
1.2 Классификация
решаемой задачи
Исходными данными в
работе является набор изображений некоторого размера.
Рассмотрим классификацию
решаемых задач искусственных нейронных сетей по книге [Терехов]. Вид исходных
данных может быть представлен в виде:
А — распознавание и классификация:
входные данные необходимо
отнести к какому-либо из известных классов при управляемом обучении
(классификации); при обучении без управления (кластеризации) сеть проводит
разделение входных образцов на группы самостоятельно, при этом все образцы
одного кластера должны иметь что-то общее — они будут оцениваться, как
подобные.
Исходными данными
является вектор признаков, выходные данные - вектор, значения всех координат
которого должны быть равными О, за исключением координаты, соответствующей
выходному элементу, представляющему искомый класс(значение этой координаты
должно быть равным 1).
К этому классу задач
также относится категоризация (кластеризация). Исходными данными является
вектор признаков, в котором отсутствуют метки классов.
В — аппроксимация функций :
предположим,
что имеется обучающая выборка ((xl yi), (х2, у2),
..., (xn, yw)), которая генерируется неизвестной
функцией, искаженной шумом. Задача аппроксимации состоит в нахождении оценки
этой функции.
Исходные данные – набор обучающих векторов. Выход сети –
рассчитанное сетью значение функции.
С --предсказание/прогноз :
пусть
заданы N дискретных отсчетов {(y(f1), y(f2), …, y(fN)} в последовательные моменты времени
t1, t2, …, tN . Задача
состоит в предсказании значения y(tN+1) в момент tN+1. Прогноз имеют значительное влияние
на принятие решений в бизнесе, науке и технике.
Исходные данные – вектора данных по M признакам за T периодов времени. Выход сети –
вектора данных по M
признакам за периоды времени T+L.
D — оптимизация:
многочисленные проблемы в математике, статистике, технике,
науке, медицине и экономике могут рассматриваться как проблемы оптимизации.
Задачей оптимизации является нахождение решения, которое удовлетворяет системе
ограничений и максимизирует или минимизирует целевую функцию.
E - Память, адресуемая по содержанию:
В модели
вычислений фон Неймана обращение к памяти доступно только посредством адреса,
который не зависит от содержания памяти. Более того, если допущена ошибка в
вычислении адреса, то может быть найдена совершенно иная информация. Память, адресуемая
по содержанию, или ассоциативная память, доступна по указанию заданного содержания.
Содержимое памяти может быть вызвано даже по частичному или искаженному
содержанию. Ассоциативная память чрезвычайно желательна при создании
перспективных информационно-вычислительных систем.
F- Управление:
Рассмотрим динамическую систему, заданную совокупностью {u(t), y(t)}, где u(t) является входным управляющим воздействием, a y(t) - выходом системы в момент времени t. В системах управления с эталонной
моделью целью управления является расчет такого входного воздействия u(t), при котором система следует по желаемой траектории,
диктуемой эталонной моделью.
Исходными данными для
данной задачи является вектора(из нулей и единиц) размерности 63, которые
описывают каждую из 9 римских цифр, выбранных для обучения. Исходные данные
предлагаются в прилагаемом файле “данные для нейросети”.
В этом же файле
содержатся и выходные вектора размерности 9, где единица в одном из 9 положений
означает принадлежность классифицируемого образца к той или иной букве.
Сеть, принимая входной
вектор, должна в соответствии с ним выдать соответствующий данной
последовательности выходной вектор.
Исходя из исходных
данных, данная задача относится к классу A- задача классификации.
1.3 Предварительный
выбор класса НС
Рассмотрим классификацию
искусственных нейронных сетей по Терехову (Управление на основе нейронных
сетей). В книге говорится о различиях вычислительных процессов в сетях,
частично обусловленных способом взаимосвязи нейронов, поэтому выделяют
следующие виды сетей , при помощи которых можно решить данную задачу:
·
сети прямого
распространения (feedforward);
·
сети с обратными
связями (feedforward /feedback);
·
гибридные сети (fuzzy).
·
некоторые модели
сетей, основанных на статических методах
Для решения нашей задачи
наиболее подходящими классами являются классы статических и динамических сетей,
так как первые позволяют довольно эффективно решать достаточно широкий диапазон
задач (наиболее известными и используемыми являются многослойные нейронные сети
, где искусственные нейроны расположены слоями. ), а вторые из-за обратных
связей состояние сети в каждый момент времени зависит от предшествующего
состояния, что позволяет эффективно обучать сеть и подстраивать весовые
коэффициенты (наиболее известны сети Хопфилда, т. к. в них происходит обучение
по обратному распространению ошибок). Также подходят сети, основанные на
статических методах (среди них можно выделить вероятностную нейронную сеть).
Сети, с помощью которых нельзя решить поставленную задачу: нечёткие структуры (fuzzy), среди которых можно выделить сети
(«самоорганизующихся карт») Кохонена, а так же сети с «радиальными базисными
функциями» активации.
Остановим свой выбор на следующих видах сетей:
·
многослойный
персептрон
·
сети Ворда
·
сети Кохонена
·
вероятностная
нейронная сеть
1.4 Предварительный
выбор структуры НС
Понятие структуры НС
включает в себя
·
Количество слоев,
·
Количество
нейронов в каждом слое,
·
Вид функции
активации,
·
Обратные связи
Входные данные для всех четырех
типов сетей одинаковые, и представляют собой вектора из 0 и 1, полученный в
результате деления растрового изображения сеткой 7х9.
Выходные данные для всех
сетей кроме сети Кохонена – вектор из нулей и единиц размерности 9, так как
число классов равно 9.
Многослойный персептрон,
как и сети Ворда, обладает тем большими интеллектуальными способностями, чем
больше число связей внутри сети.
Число скрытых нейронов
для этих классов сетей определим по формуле:
N скрытых нейронов =
1/2 (Nвходов + Nвыходов) + корень квадратный из количества тренировочных
примеров.
Число входных нейронов
63. Число выходных 9. По формуле число скрытых нейронов 48.
Определим число слоев:
Число связей при 1
скрытом слое равно (между слоями каждый нейрон соединен с каждым):
63*48+48*9=3456
при 2 скрытых слоях:
63*24+24*24+24*9=2304
при 3 слоях:
63*16+16*16+16*16+16*9=1664
Таким образом оптимальное
число скрытых слоев равно 2.
В вероятностной нейронной
сети и сети Кохонена выбор числа входных нейронов равен числу примеров (в нашем
случае 63), а выходных – числу категорий (в нашем случае 9).
Для ВНС число скрытых
нейронов должно быть не менее числа примеров (в нашем случае 10 – на 1 боле
числа примеров).
вид функций активации: зависит от окончательного выбора
модели и структуры (наиболее подходящими являются логистическая (сигмоидальная)
и линейная).
Скорость обучения выберем
исходя из того, что при очень большой скорости сеть может обучиться неверно, а
при очень маленькой процесс обучения может быть долгим.
1.5 Выбор пакета НС
Выбор пакета основывался
на следующих принципах:
• Доступность пакета;
• Полнота пакета (наличие
необходимых моделей сети, достаточного количества параметров для построения и
обучения нейронных сетей);
• Простота использования;
• Русифицированная
документация
• Работа с .bmp файлами
Опираясь
на [Круглов, Борисов] проведем сравнительный анализ нескольких пакетов:
1) NeuroPro
2) NeuroShell 2
3) NeuroShell Classifier v2.0
4) QwikNet32 v2.1
5) Neural Planner
Нейропакет NeuroPro
Возможности программы:
1) Работа (чтение, запись, редактирование) с файлами данных,
представленными в форматах *.dbf
(СУБД dBase, FoxPro, Clipper)
и *.db (СУБД Paradox).
Создание слоистых нейронных сетей для решения задач
прогнозирования:
• число слоев нейронов - до 10;
• число нейронов в слое - до 100;
• нейроны: с нелинейной сигмоидальной функцией активации f(A) = А/(|А| + с), крутизна сигмоиды
может задаваться отдельно т для каждого слоя нейронов.
Нейронная сеть может одновременно решать несколько задач
прогнозирования; для каждого из выходных сигналов могут быть установлены свои
требования к точности прогнозирования.
2) Обучение нейронной сети производится по принципу
двойственного функционирования с применением одного из следующих методов оптимизации:
• градиентного спуска;
• модифицированного ParTan - метода;
• метода сопряженных градиентов.
Работа с .bmp файлами: нет.
Руководство: есть.
Наличие пакета: есть.
Нейропакет NeuroShell 2
Для начинающего
пользователя непонятный интерфейс.
Обучающая выборка
формируется достаточно просто, поддерживает импорт таблиц с входными данными в
формате Excel или Lotus.
Работа с .bmp файлами: нет.
Наличие пакета: есть.
Руководство: есть
(русифицированное).
Кроме русскоязычного
руководства, есть учебник по NeuroShell 2.
Нейропакет реализует
широкий круг типов нейронных сетей.
Нейропакет NeuroShell Classifier v2.0
Этот пакет является
средством разработки нейронносетевых приложений, для решения проблем
классификации. Поддержка генетических алгоритмов.
Работа с .bmp файлами: нет.
Руководство: есть.
Пакет на английском
языке.
Наличие пакета: есть.
Нейропакет QwikNet32 v2.1
В QwikNet реализуется лишь один тип нейронной
сети - многослойная сеть прямого распространения с числом скрытых слоев до 5 и
с набором из 6 алгоритмов обучения (модификации алгоритма обратного
распространения ошибки).
Работа с .bmp файлами: нет.
Руководство: есть
(русифицированное).
Пакет на английском
языке.
Наличие пакета: нет.
Нейропакет Neural Planner
Предназначен для решения
различных задач классификации объектов, обработки значений случайных процессов,
решения некоторых математических задач, создания эффективных экспертных систем.
Работа с .bmp файлами: нет.
Руководство: есть
(русифицированное).
Пакет на английском
языке.
Наличие пакета: нет.
Таблица 1 Сравнение
пакетов
| Пакет |
Доступность |
Наличие необходимых
моделей НС |
Русификация /
руководство на русском |
Работа с .bmp |
| Neural Planner |
нет |
есть |
нет / есть |
нет |
| QwikNet32 v2.1 |
нет |
нет |
нет / есть |
нет |
| NeuroShell Classifier v2.0 |
есть |
есть |
нет / нет |
нет |
| NeuroShell 2 |
есть |
есть |
есть / есть |
нет |
| NeuroPro |
есть |
нет |
нет / есть |
нет |
Исходя из сравнительного
анализа нейропакетов останавливаем свой выбор на продукте NeuroShell 2.
1.6 Минимальные требования к
информационной и программной совместимости
Microsoft
Office 2000, XP
Пакет NeuroShell 2
Графический редактор (Paint)
1.7 Минимальные требования к составу
и параметрам технических средств
Операционная система Windows 95 или выше
32 Мб ОЗУ
500 Кб HDD
2. Обучение НС
2.1 Формирование исходных данных
В качестве исходных
данных в задаче выступает графическое изображение римских цифр с различными
вариациями. Поскольку в выбранном пакете нет графического редактора, изображение
преобразуют в последовательность нулей и единиц по определенным правилам.
Данный пакет позволяет
подавать на вход нейросети порядка 32000 значений для одной обучающей пары, но
необходимо ограничить размер входного изображения, т.к. MS Excel XP имеет максимальное число столбцов 256.
При создании входного
вектора мы руководствовались несколькими критериями:
· Макимальная различимость
· Минимальный размер
Изначально
рассматривались различные варианты размерности входного вектора.
Минимально для
различимости символов высота изображения цифры требуется 7 пикселей, т.к. 2
пиксела идет на изображение подчеркивания (это является особенностью написания
римских цифр), а оставшиеся 5 на сам символ. На сетке меньшей высоты теряется
различимость. Для определения второго параметра изображения мы брали в расчет
те цифры, для написания которых требуется максимальная ширина сетки: это цифры
7 и 8. При написании этих цифр минимальной оказалась ширина = 9 пикселам. Дело
в том что эти цифры состоят из нескольких символов: основной символ,
изображающий цифру 5 либо 10, а также дополнительные, которые показывают
сколько к основной цифре нужно добавить (либо отнять) единиц, чтобы получилась
искомая. А поскольку именно в эти цифры входит максимально для наших данных по
два дополнительных символа, два пиксела мы оставляем на промежуток между
символами и основной символ, нам потребовалось не менее 9 пикселей.
Таким образом для
моделирования был выбран размер изображения 7x9 пикселей.
Обучающая пара содержит 63+9=72
значения.
Представили 144 объекта
различной формы.
В Excel получили файл, таблицу с обучающими
параметрами.
Наш объект заносится в
таблицу при помощи нулей и единиц, т.е. формируется соответствующий массив,
записанный в одну строку, также в процессе обучения используются реальные
выходные значения, которые записаны как одно значения в конце строки
сформированного массива. Объекты, расположение которых должно быть выучено
сетью, представляются размерной сеткой (7x9), где темным пикселям (частям объекта) соответствуют 1, а
белым (пустое пространство) – 0.
 
изображение римской цифры
9.
изображение умышленно
перевернуто нами для достижения лучшей терпимости сети к подаваемому углу
изображения.
2.2 Окончательный выбор модели, структуры НС
По рекомендациям
разработчиков пакета критерием остановки обучения будет:
события после минимума
> 20000, так как с использованием встроенной калибровки этот критерий
позволяет избежать переучивания сети и запоминания тестовых примеров.
Рассмотрим наиболее
подходящие сети для решения данной задачи. Основные параметры, такие как виды
функций активации: скорость обучения (=0,1),веса (=0,3),момент равен (=0,1)
По умолчанию для
предсказания рекомендуется использовать сеть Ворда, содержащую два скрытых
блока с разными передаточными функциями.
Стандартные сети.
Попробуем провести
обучение с помощью модели 4-хслойной сети, в которой каждый слой
соединён только с предыдущим слоем.
Структура НС:
1.
количество слоев:
4
2.
количество
нейронов:
а) во входном слое: 63
б) в выходном слое: 9
3. вид функций активации:
а) входной слой –
линейная [0;1]
б) выходной слой –
логистическая
В таблице отражена
зависимость минимальной средней ошибки на тренировочном и тестовом наборах от
количества нейронов в скрытом слое.
Скорость обучения = 0,1;
момент = 0,1; скрытые слои – слой 1 – 24 нейрона, слой 2 – 24 нейрона.
Таблица данных
| Время обучения |
Функции активации |
Min средняя ошибка |
| 1слой |
2слой |
на тренировочном наборе |
на тестовом наборе |
| 03:18 |
логистическая |
логистическая |
0,0000036 |
0,0002548 |
| 08:03 |
Гауссова |
Гауссова |
0,0000006 |
0,0003652 |
| 00:05 |
линейная |
линейная |
0,5047548 |
0,7126971 |
| 01:01 |
компГауссова |
компГауссова |
0,0000059 |
0,0004709 |
Исходя из таблицы,
оптимальной структурой для данной сети являестся сесть с Гауссовыми
активационными функциями.
|
|
Вых1 |
Вых2 |
Вых3 |
Вых4 |
Вых5 |
Вых6 |
Вых7 |
Вых8 |
Вых9 |
| R квадрат |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
0,9995 |
1,0000 |
0,9999 |
| СКО |
0,002 |
0,002 |
0,001 |
0,001 |
0,001 |
0,002 |
0,007 |
0,001 |
0,004 |
| Относ СКО % |
0,155 |
0,195 |
0,073 |
0,057 |
0,082 |
0,166 |
0,722 |
0,084 |
0,351 |
НС после обучения показывает
не очень хорошие обобщающие данные. Неплохие обобщающие данные сеть в середине
интервала.
Скорость обучения и
начальный момент на качество обобщения не влияют.
Сеть Ворда с двумя
блоками в скрытом слое.
Структура НС:
1. количество слоев: 4
2. количество нейронов:
а) во входном слое: 63
б) в выходном слое: 9
В таблице отражена
зависимость минимальной средней ошибки на тренировочном и тестовом наборах и
времени обучения от вида функций активации.
Скорость обучения = 0,1;
момент = 0,1
Таблица данных
| 1 скрытый слой |
2 скрытый слой |
Min средняя ошибка |
Время обучения |
| Функция активации |
Кол-во нейронов |
Функция активации |
Кол-во нейронов |
на тренировочном наборе |
на тестовом наборе |
| Комп.Гауссова |
24 |
Комп. Гауссова |
24 |
0,0000016 |
0,0005358 |
04:42 |
| Гауссова |
24 |
Гауссова |
24 |
0,0000017 |
0,0019529 |
03:58 |
| логистическая |
24 |
логистическая |
24 |
0,0000058 |
0,0003688 |
02:18 |
| логистическая |
24 |
Комп.Гауссова |
24 |
0,0000043 |
0,0006007 |
01:35 |
Исходя из таблицы дла
данной сети оптимальными будут гауссовы функции активации.
|
|
Вых1 |
Вых2 |
Вых3 |
Вых4 |
Вых5 |
Вых6 |
Вых7 |
Вых8 |
Вых9 |
| R квадрат |
1.0000 |
0.9992 |
0.9999 |
1.0000 |
0.9999 |
1.0000 |
0.9995 |
1.0000 |
1.0000 |
| СКО |
0.002 |
0.009 |
0.003 |
0.001 |
0.003 |
0.001 |
0.021 |
0.001 |
0.002 |
| Относ СКО % |
0.152 |
0.910 |
0.275 |
0.107 |
0.320 |
0.133 |
2.112 |
0.128 |
0.153 |
Данная сеть после обучения
показывает хорошие обобщающие данные.
Скорость обучения и
начальный момент на качество обобщения не влияют.
Сеть Ворда с двумя
блоками в скрытом слое и с обходным соединением
Структура НС:
1.
количество слоев:
4
2.
количество
нейронов:
а) во входном слое: 63
б) в выходном слое: 9
3. активационная функция
а) во входном слое: линейная
б) в выходном:
логистическая
В таблице отражена
зависимость минимальной средней ошибки на тренировочном и тестовом наборах и
времени обучения от вида функций активации.
Скорость обучения = 0,1;
момент = 0,1
Таблица данных
| 1 скрытый слой |
2 скрытый слой |
Min средняя ошибка |
Время обучения |
| Функция активации |
Кол-во нейронов |
Функция активации |
Кол-во нейронов |
на тренировочном наборе |
на тестовом наборе |
| Гауссова |
24 |
компГауссова |
24 |
0,0000013 |
0,0034898 |
02:59 |
| Гауссова |
24 |
Гауссова |
24 |
0,0000005 |
0,0065507 |
05:21 |
| компГауссова |
24 |
компГауссова |
24 |
0,0000017 |
0,0037426 |
02:29 |
| логистческая |
24 |
логистическая |
24 |
0,0000147 |
0,0019549 |
00:38 |
Исходя из таблицы дла
данной сети оптимальными будут функции активации Гауссова для 1 слоя и Комплем.
Гауссова для 2 слоя.
|
|
Вых1 |
Вых2 |
Вых3 |
Вых4 |
Вых5 |
Вых6 |
Вых7 |
Вых8 |
Вых9 |
| R квадрат |
0,9995 |
0,9995 |
0,9986 |
0,9995 |
0,9983 |
0,9994 |
0,9996 |
0,9977 |
0,9979 |
| СКО |
0,007 |
0,008 |
0,013 |
0,007 |
0,012 |
0,007 |
0,006 |
0,014 |
0,015 |
| Относ СКО % |
0,690 |
0,760 |
1,258 |
0,692 |
1,230 |
0,746 |
0,620 |
1,429 |
1,512 |
Данная сеть после
обучения показывает не очень хорошие обобщающие данные.
Скорость обучения и
начальный момент на качество обобщения не влияют.
Сеть Кохонена
Структура НС:
1.
кол-во нейронов
a.
входной слой: 63
b. выходной слой: 9
2.
скорость
обучения: 0,5
3.
начальные веса:
0,5
4.
окрестность: 8
5.
эпохи: 500
в таблице отражена
зависимость средней количества неиспользованных категорий от пораметров выбора
примеров и метрик расстояния.
| Параметры выбора примеров |
Метрики расстояния |
Время обучения |
Кол-во неиспозльзованных категорий |
| поочередный |
евклидова |
00:02 |
1 |
| случайный |
евклидова |
00:02 |
1 |
| поочередный |
нормированная |
00:02 |
3 |
| случайный |
нормированная |
00:02 |
2 |
Данная сеть обладает
плохим обобщением.
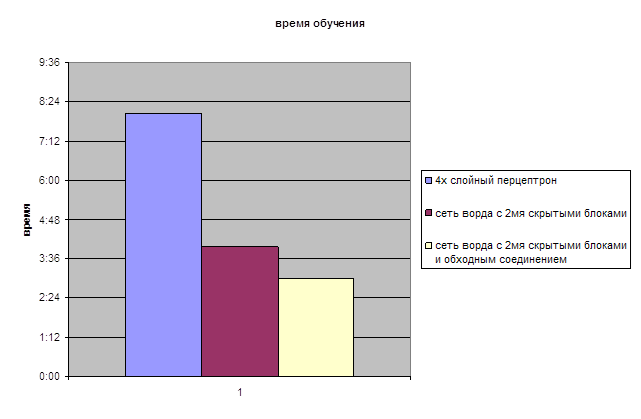
На данной диаграмме
показаны сравнительные данные по времени обучения рассмотренных сетей.
Т.к сеть Кохонена
обладает наихудшими обобщением, ее в диаграмму не включаем.
На данной диаграмме
показаны сравниваемые нами значения выходных данных обученных сетей.
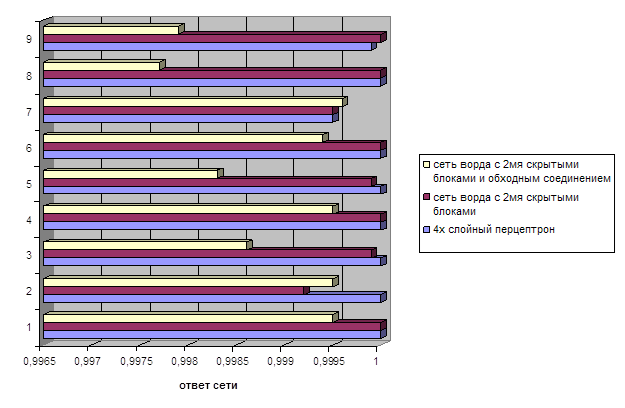
Исходя из представленных
диаграмм оптимальной для нас будет сеть Ворда с 2мя скрытыми блоками.
2.3 Выбор параметров
обучения
Находим оптимальные
параметры:
• скорость обучения в интервале от 0
до1
• момент в интервале от 0 до 1
• начальные веса от 0 до 1
1. Зависимость
качества обучения от скорости обучения
| Скорость обучения |
0,1 |
0,5 |
0,7 |
1 |
| Мин. ср. ошибка на тест. наборе |
0,0019529 |
0,0006956 |
0,0005016 |
0,0002641 |
2.Зависимость качества
обучения от момента
| Момент |
0,1 |
0,5 |
0,7 |
1 |
| Мин. ср. ошибка на тест. наборе |
0,0019529 |
0,0012411 |
0,0013824 |
0,5690943 |
3.Зависимость качества
обучения от начальных весов
| Начальный вес |
0,1 |
0,3 |
0,7 |
1 |
| Мин. ср. ошибка на тест. наборе |
0,0010359 |
0,0019529 |
0,0032182 |
0,0031102 |
2.4 Оптимальные
параметры обучения
Скорость обучения: 0,1
Начальный момент: 0,1
Начальные веса: 0,3
Модель - Сеть Ворда с
двумя блоками в скрытом слое.
Структура НС:
1.
количество слоев:
4
2.
количество
нейронов:
1)
блок 1: 63
2)
блок 2: 24
3)
блок 3: 24
4)
блок 4: 9
3. вид функций активации:
1)
блок 1 – линейная
[0;1]
2)
блок 2 –гауссова
3)
блок 3 –гауссова
4)
блок 5 –
логистическая.
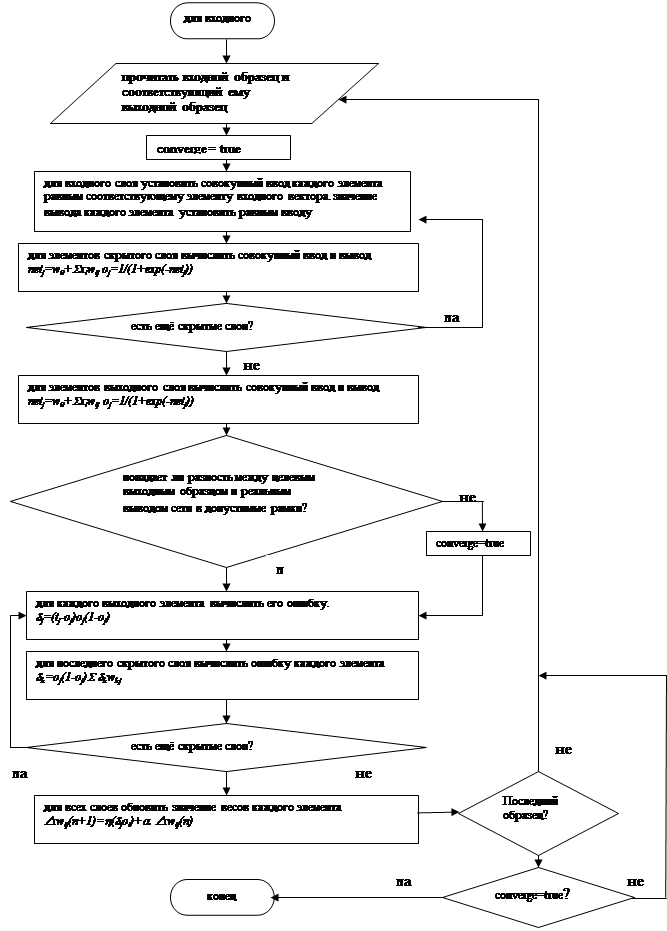
2.5
Блок-схема алгоритма обучения
3.
Анализ качества обучения
При данных оптимальных
параметрах результаты применения сети можно представить виде таблицы
|
|
Вых1 |
Вых2 |
Вых3 |
Вых4 |
Вых5 |
Вых6 |
Вых7 |
Вых8 |
Вых9 |
| R квадрат |
1.0000 |
0.9992 |
0.9999 |
1.0000 |
0.9999 |
1.0000 |
0.9995 |
1.0000 |
1.0000 |
| СКО |
0.002 |
0.009 |
0.003 |
0.001 |
0.003 |
0.001 |
0.021 |
0.001 |
0.002 |
| Относ СКО % |
0.152 |
0.910 |
0.275 |
0.107 |
0.320 |
0.133 |
2.112 |
0.128 |
0.153 |
| доля с ош <5% |
10.417 |
12.500 |
13.194 |
9.722 |
9.722 |
11.111 |
10.417 |
9.722 |
12.500 |
| доля с ош 5-10% |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| доля с ош 10-20% |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| доля с ош 20-30% |
0 |
0 |
0 |
0 |
0 |
0 |
0.694 |
0 |
0 |
| доля с ош >30% |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Для проверки способностей
к обобщению на вход сети подаются зашумленные последовательности входных
сигналов. Процент зашумления показывает, какое количество битов входного
вектора было инвертировано по отношению к размерности входного вектора.
Для зашумления 5% сеть
выдает такие результаты:
|
|
Вых1 |
Вых2 |
Вых3 |
Вых4 |
Вых5 |
Вых6 |
Вых7 |
Вых8 |
Вых9 |
| Rквадрат |
0,9868 |
0,9884 |
0,9800 |
0,9831 |
0,9843 |
0,9830 |
0,9814 |
0,9855 |
0,9838 |
| СКО |
0,036 |
0,034 |
0,044 |
0,041 |
0,039 |
0,041 |
0,043 |
0,038 |
0,040 |
| Относ СКО % |
3,616 |
3,385 |
4,448 |
4,089 |
3,942 |
4,096 |
4,289 |
3,781 |
3,998 |
| доля с ош<5% |
11,111 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| доля с ош5-10% |
0 |
11,111 |
11,111 |
0 |
0 |
11,111 |
0 |
11,111 |
11,111 |
| доля с ош 10-20% |
0 |
0 |
0 |
11,111 |
11,111 |
0 |
11,111 |
0 |
0 |
| доля с ош 20-30% |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| доля с ош>30% |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Далее мы подавали
различное количество инвертированных битов.
В таблице представлена
зависимость количества инвертированных битов от количества правильных ответов
на выходе
| Количество инвертированных битов |
Количество верных ответов на выходе |
| 50 |
0 |
| 25 |
2 |
| 13 |
9 |
| 19 |
6 |
| 16 |
7 |
| 15 |
8 |
| 14 |
8 |
Таким образом мы выявили
критическое количество зашумленных данных = 16 на каждый входной вектор.
Это соответствует 20%
зашумления. При большем зашумлении входных данных сеть не может отдать
предпочтение одной цифре, причем с увеличением зашумления количество таких букв
растет.
Результаты сети при
критическом зашумлении:
|
|
Вых1 |
Вых2 |
Вых3 |
Вых4 |
Вых5 |
Вых6 |
Вых7 |
Вых8 |
Вых9 |
| R квадрат |
0,7193 |
0,8274 |
0,6583 |
0,7303 |
0,7928 |
0,6981 |
0,9135 |
0,8702 |
0,7746 |
| СКО |
0,028 |
0,017 |
0,034 |
0,027 |
0,020 |
0,030 |
0,009 |
0,013 |
0,022 |
| Относ СКО % |
16,650 |
13,057 |
18,369 |
16,322 |
14,304 |
17,268 |
9,243 |
11,321 |
14,922 |
| доля с ош <5% |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| доля с ош 5-10% |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| доля с ош 10-20% |
0 |
11,111 |
0 |
0 |
11,111 |
0 |
0 |
0 |
0 |
| доля с ош 20-30% |
0 |
0 |
0 |
0 |
0 |
0 |
11,111 |
0 |
11,111 |
| доля с ош >30% |
11,111 |
0 |
11,111 |
11,111 |
0 |
11,111 |
0 |
11,111 |
0 |
Судя по анализу качества
обучения, сеть хорошо справляется при 20% зашумлении.
Это говорит о том что у
сети неплохой потенциал для обобщения.
Выводы
В ходе данной курсовой
работы были получены навыки моделирования нейронных сетей, а также была решена
частная задача моделирования нейронной сети для классификации римских цифр.
Исходными данными для сети являлись изображения римских цифр, представленные
виде матриц, размерностью 7х9.
Обученная нейронная сеть
хорошо себя показала при 20% уровне шума. Для увеличения этого показателя нужно
снизить риск возникновения критических шумов. Этого можно достигнуть путем
увеличения размерности сетки.
Список использованных источников
1
Стандарт
предприятия СТП 1–У–НГТУ–98
2
Круглов В.В.,
Борисов В.В. Искусственные нейронные сети. Теория и практика. – М.: Горячая
линия – Телеком, 2001. – 382 с.:ил.
3
Электронный
учебник по NeuroShell 2
4
Каллан Р.
Основные концепции нейронных сетей
5
Ресурсы сети
Интернет
|