Контрольная работа: Виды умозаключений
Контрольная работа: Виды умозаключений
УМОЗАКЛЮЧЕНИЕ
План
1.
Общее понятие об умозаключении
2.
Простой категорический силлогизм
3.
Общие правила силлогизма
4.
Фигуры категорического силлогизма
5.
Модусы категорического силлогизма
6.
Сокращенные и сложные силлогизмы
7.
Условные, разделительные и условно-разделительные силлогизмы
8. Индуктивные умозаключения
1. Общее понятие об умозаключении
В
процессе познания очевидные утверждения составляют лишь часть всех истин.
Обычно для установления истины приходится в каждом случае производить особое
исследование, т.е. четко поставить вопрос, принять во внимание ранее
установленные истины, собрать необходимые факты, поставить опыты, осмыслить их
результат, проверить на практике возникшие догадки и т.д.
Установление
истины возможно и логическим путем. Происходит это с помощью рассуждений.
Рассуждением называется ряд суждений, которые относятся к определенному
предмету или вопросу, идут одно за другим таким образом, что из предшествующих
суждений с необходимостью или высокой вероятностью следуют другие, а в
результате получается единственно правильный либо приемлемый ответ на
поставленный вопрос. Признавая истинным предшествующие суждения, мы должны
признавать истинным и вытекающие из них суждения. То логическое действие,
посредством которого обнаруживается истинность новых суждений, называется
умозаключением.
Умозаключение – это форма мышления, в которой из
одного или нескольких истинных суждений на основании определенных правил вывода
получается новое суждение, которое с непреложностью ил определенной степенью
вероятности следует из них.
Какова
структура умозаключения?
Элементами
любого умозаключения являются простые или сложные суждения. Суждения, из
которых можно получить новое знание и из которых, раз они признаны истинными, с
необходимостью следует какое-либо новое суждение, называются посылками
умозаключения. Суждение, которое признается истинным и получено путем
умозаключения, называется выводом, или заключением, или логическим следствием.
Например, из двух посылок: (1) «Студент Иванов – член сборной команды
университета по баскетболу» и (2) «Студент Краснов на всех соревнованиях по
баскетболу эффективно играет в паре со студентом Ивановым» следует вывод
(заключение, логическое следствие): (3) «Студент Краснов – член сборной команды
университета по баскетболу».
Формальная
логика специально занимается установлением правил, соблюдение которых
обеспечивало бы надежный истинный вывод.
Каковы же
условия истинности выводов?
Первое
условие: истинность выводов зависит от истинности посылок умозаключения. При
наличии хотя бы одного ложного (полностью или частично) суждения (посылки)
вывод истинным быть не может. Это потому, что вывод следует из посылок как
мысль, связанная с посылками необходимой логической связью.
Второе
условие: истинность выводов зависит от наличия правильной логической связи
между посылками, а также между посылками и выводом. Эти правильные логические
связи есть законы формальной логики. Но правила вывода обеспечивают лишь
формальную правильность умозаключения. Если все множество суждений, которое мы
берем в качестве посылок, представляет собой несомненные истины, то логически
неверное связывание их никогда не сможет дать обоснованного правильного вывода.
По степени
общности и посылок умозаключения делятся на три группы:
1) дедуктивные,
в которых мысль идет от большей к меньшей общности знания;
2) индуктивные,
когда мысль развивается от знания одной степени общности к новому знанию,
большей степени общности;
3) умозаключения
по аналогии, у которых посылки и выводы выражают знание одинаковой степени
общности.
В отдельных
дедуктивных заключениях можно идти от единичного к частному (единичное суждение
приравнивается к общему), но непременным остается ход мысли от общего к
частному или единичному. Для дедукции характерно подведение частного случая под
общее правило или выведение (deductio) из общего правила следствий относительно
частного случая. Поэтому выводы дедуктивного умозаключения обладают
достоверностью и носят принудительный характер.
Посылками
дедуктивного умозаключения могут быть суждения всех типов логических союзов –
категорические, разделительные, условные суждения или разнообразное их
сочетание, определяющее характер вывода. Соответственно этому дедуктивные
умозаключения бывают: категорические, разделительно-категорические и
условно-разделительные.
Рассмотрение
дедуктивных умозаключений принято начинать с категорических, с особой, наиболее
типичной для дедукции формы этих умозаключений, называемой силлогизмом (от
греч. syllogismos – сосчитывание).
2. Простой категорический силлогизм
Силлогизм –
это дедуктивное умозаключение, в котором из двух категорических суждений –
посылок, связанных общим термином, получается третье суждение – вывод.
На самом
простом примере проанализируем структуру силлогизма: «Все планеты светят
отраженным светом. Земля – планета. Следовательно, Земля светит отраженным
светом». Вывод этого силлогизма представляет собой простое категорическое
суждение А, в котором объем предиката (тела, способного отражать свет) шире
объема субъекта (Земля). В силу этого предикат вывода называется большим
термином, а субъект вывода – меньшим термином. Соответственно этому посылка, в
которую входит предикат вывода, т.е. большой термин, называется большой
посылкой, а посылка с меньшим термином, субъектом вывода, называется меньшей
посылкой силлогизма.
Третье
понятие «планета», посредством которого устанавливается связь между большим и
меньшим терминами, называется средним термином силлогизма и обозначается
символом М (medium – посредник). Средний термин входит в каждую посылку, но не входит
в заключение. Назначение среднего термина – быть связующим звеном между
крайними терминами, между субъектом и предикатом вывода.
Эта связь
осуществляется в посылках: в большей посылке средний термин связан с предикатом
(М – Р), в меньшей посылке – с субъектом вывода (S – М). В итоге мы получаем
следующую общую схему силлогизма:
| M – P |
|
S – M |
|
| S – M |
Или |
M – P |
(S – M – P) |
| S – P |
|
S – P |
|
При этом
нужно иметь в виду:
1)
наименования «большая» или «меньшая» посылка зависит не от местоположения в
схеме силлогизма, а только от наличия в ней большего или меньшего термина;
2) с
переменой места любого термина в посылке обозначение его не меняется – больший
термин (предикат вывода) всегда обозначается символом Р, меньший (субъект
вывода) – символом S, средний – символом М;
3) от
перемены порядка посылок в силлогизме вывод, то есть логическая связь между
крайними терминами, не зависит.
Таким
образом, логический анализ силлогизма нужно начинать с вывода, с уяснения его
субъекта и предиката, с установления отсюда меньшего и большего терминов
силлогизма. В зависимости от этого выделяется большая и меньшая посылка, а
также средний термин, повторяющийся в обеих посылках.
При
построении силлогизма нужно следить за подбором посылок, позволяющих по
содержанию сделать объективный вывод. При этом необходимо строго учитывать
логическое основание всякого силлогистического вывода, так называемую аксиому
силлогизма.
Аксиома
силлогизма выражается так: все, что утверждается относительно всего класса
предметов, распространяется на любой предмет этого класса. Что верно
относительно рода, то верно и относительно всех предметов или видов этого рода.
И наоборот – не присуще роду, то не присуще и видам, входящим в данный род.
Отражая
объективные свойства и отношения вещей, аксиома силлогизма выражает связь
понятий – терминов прежде всего по их содержанию. Но так как связь понятий по
содержанию определяет их отношение по объему, то аксиома выражает также
объемные отношения терминов силлогизма. Эти отношения можно выразить круговыми
схемами, показав несовместимость или совместимость объемов понятий, отражающих
признаки определенных классов предметов (Рис. 1 и 2).
Рис. 1 Рис. 2
Название
«аксиома» силлогизма означает, что правило не требует доказательства:
многократно подтвержденное опытом, оно стало очевидным.
3. Общие правила силлогизма
Структура
силлогизма подчинена определенным логическим правилам, без соблюдения которых
невозможно построить силлогизм. Эти правила можно разбить на две группы:
правила терминов и правила посылок.
а) Правила
терминов.
1. В каждом силлогизме должно
быть только три термина – большой, меньший и средний. Это правила требует не
только соответствующего построения силлогизма, но и однозначности среднего
термина в обеих посылках. Повторяясь в большей и меньшей посылках, он может
потерять свою однозначность, и тогда правильный вывод получить невозможно, ибо
не будет связующего звена между крайними терминами. Так получается в следующем
силлогизме: «Труд – основа жизни. Изучение логики – труд. Следовательно,
изучение логики – основа жизни». Понятие труд в каждой посылке взято не
однозначно: в первом случае оно означает деятельность как общую форму бытия
человека, во втором – как конкретный вид работы ума.
2. Средний термин должен
быть распределен, то есть взят в полном объеме, хотя бы в одной из посылок. Для
этого он должен быть или субъектом общего суждения, или предикатом
отрицательного суждения. Если же средний термин взят не в полном объеме в обеих
посылках, то выполнить свою роль связующего звена он не сможет, и точный вывод
получить невозможно. Например, в посылках «Некоторые студенты – мастера спорта»
и «Все старосты учебных групп – студенты» средний термин «студенты» не
распределен, поэтому сделать вывод, есть ли мастера спорта среди старост групп
не представляется возможным. (Рис. 3).
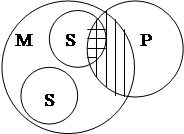
Рис. 3
Из рисунка
видно, что объем субъекта («все старосты учебных групп») может перекрещиваться
с объемом большего термина («мастера спорта»), но может находиться и вне его.
3. Термин, не распределенный
в посылках, не может быть распределен в заключении. Из общих суждений-посылок:
«Все птицы летают с помощью крыльев» и «Все птицы – теплокровные животные»
нельзя получить в качестве вывода общее суждение. Меньший термин «теплокровные
животные» стоит на месте предиката в утвердительной посылке и поэтому не
распределен. Следовательно, в выводе его нужно брать не в полном объеме. (Рис. 4).

Рис. 4
б)
Правила посылок.
4. Из двух
частных посылок невозможно сделать вывод. В этом случае нельзя установить
объемные отношения между терминами силлогизма, поэтому определенный вывод не
получается. Например, из посылок: «Некоторые члены Академии наук – химики» и
«Некоторые биологи – члены Академии наук» никакой определенный вывод не
следует. Объем субъекта («некоторые биологи») может перекрещиваться в какой-то
мере с объемом предиката («химики»), но может находиться и вне его, как
показано на рисунке 5.
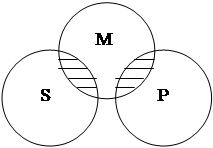
Рис. 5
Если одна
посылка частная, то вывод будет частным.
Из посылок:
«Все участники кросса – спортсмены» и «Некоторые студенты-отличники – участники
кросса» общий вывод невозможен. Нельзя утверждать, что все студенты-отличники –
спортсмены, так как речь идет только о части объема меньшего термина.
5. Из двух отрицательных
посылок нельзя сделать вывод.
В этом случае все термины исключают друг друга, устраняя
всякую объемную взаимосвязь между ними. Из посылок: «Ни одна планета не светит
собственным светом» и «Искусственный спутник не есть планета» – никакого вывода
не следует.
6. Если одна посылка
отрицательная, то вывод будет отрицательным. Например: «Всякое пребывание на
свежем воздухе полезно. Пребывание на свежем воздухе при низкой температуре
опасно. Следовательно, пребывание на свежем воздухе при низкой температуре
может принести вред здоровью». (Рис. 6).

Рис. 6
Таковы общие правила, которые следует учитывать при
составлении силлогизма.
4. Фигуры категорического силлогизма
Силлогизмы различаются
положением среднего термина в суждениях-посылках: он может стоять на месте
субъекта или на месте предиката. Этим определяется и положение крайних
терминов, а значит, и возможность и характер вывода.
В зависимости
от положения среднего термина различаются четыре фигуры силлогизма: 1) средний
термин может стоять на месте субъекта в большей посылке и предиката в меньшей;
2) он может быть предикатом в обеих посылках; 3) средний термин может оказаться
субъектом в обеих посылках; 4) он может стать предикатом в большей и субъектом –
в меньшей посылке. Различное местоположение среднего термина можно выразить в
виде таких схем:
М – Р Р – М М – Р Р – М
S –
M S – M M – S M – S
1 фигура 2
фигура 3 фигура 4 фигура
(предполагается,
что большая посылка ставится первой, а меньшая – второй).
Различия
силлогизмов в зависимости от местоположения среднего термина в посылках
называется фигурами силлогизма. Все силлогизмы делятся по этим четырем фигурам.
От местоположения среднего термина в посылках зависит количественный и
качественный характер вывода, а также сама возможность его получения.
Только по 1-й
фигуре можно получить выводы всех основных видов суждения. По 2-й фигуре
получается только отрицательный вывод. По 3-ей фигуре вывод всегда будет
частным суждением. 4-я фигура силлогизма вовсе не употребляется, ибо такое
расположение терминов не дает вывода или он будет иметь слишком ограниченное
познавательное значение.
Учитывая
требования общих правил силлогизма, можно применительно к размещению терминов в
каждой фигуре вывести четыре правила фигур силлогизма.
Для 1-ой
фигуры: меньшая посылка должна быть утвердительной, а большая – общей (иначе
будут нарушены правила 2-е и 3-е).
Допустим, что
меньшая посылка – отрицательное суждение, а большая посылка – утвердительное (обе
посылки отрицательными быть не могут). При отрицательной посылке вывод всегда
будет отрицательный (в силу 7-го правила). В отрицательном выводе больший
термин должен быть распределен, в то время как в утвердительной большой посылке
он не распределен – нарушение 3-го правила. Следовательно, меньшая посылка
должна быть утвердительной, а большая посылка – общим суждением, чтобы средний
термин был распределен хотя бы в одной из посылок (2-е правило).
Для 2-ой
фигуры: одна посылка должна быть отрицательной, а большая – общей (иначе будут
нарушены правила 2-е и 3-е).
Если обе
посылки будут представлены утвердительными суждениями, тогда средний термин,
занимающий место предиката в обеих посылках, будет не распределен – нарушение 2-го
правила. Следовательно, одна посылка, а значит, и вывод должны быть
отрицательными. В отрицательном выводе больший термин (предикат) распределен. В
таком случае, согласно3-му правилу, нужно взять в качестве большей посылки
общее суждение (все Р есть, не есть М).
Для 3-ей
фигуры: меньшая посылка должна быть утвердительной, а вывод всегда будет
частным (иначе нарушается 3-е правило).
В самом деле,
если меньшая посылка и вывод отрицательны, тогда больший термин в заключении
будет распределен при нераспределенности его в утвердительной большей посылке –
нарушение 3-го правила. Значит, меньшая посылка должна быть утвердительной, но
тогда нераспределенный меньший термин, стоящий в ней на месте предиката, в
выводе будет взят с ограничением («некоторые»), то есть вывод будет частным
суждением.
Неоднородный
характер выводов по каждой фигуре силлогизма определяется различия в их
назначении.
1-ю фигуру
силлогизма можно назвать фигурой подчинения, подведения частного случая под
общее положение, закон, принцип. Например: «Всякое тело имеет форму. Луна –
небесное тело. Следовательно, Луна имеет форму».
Назначение 2-ой
фигуры силлогизма – получение вывода в тех случаях, когда предметы одного
класса исключаются из другого класса на том основании, что им не присущи
признаки этого класса: это фигура опровержения ложной дедукции. Например: «Ни
один материалист не признает существования Бога. Некоторые материалисты в
истории философии признавали существование Бога. Следовательно, некоторые
материалисты не были материалистами».
3-я фигура
силлогизма носит характер опровержения кажущейся несовместимости совместимых
понятий. Например: «Борьба с организованной преступностью – справедливое
деяние. Борьба с организованной преступностью есть насилие. Некоторое насилие –
справедливо».
Знание и учет
характеристик фигур силлогизма позволит сознательно их использовать в каждом
конкретном случае для получения нового знания о предмете мысли.
5. Модусы категорического силлогизма
Модусами
называются виды силлогизма, различающиеся количественным и качественным
характером посылок.
По
каждой фигуре силлогизма есть определенные сочетания посылок, дающие правильный
вывод. Некоторые же сочетания противоречат основным правилам (и аксиоме)
силлогизма, поэтому правильных выводов дать не могут. Отсюда возникает
необходимость установить правильные модусы каждой фигуры.
На примере 1-ой
фигуры силлогизма можно уяснить методику выведения правильных модусов. Для
этого рассмотрим все возможные сочетания основных видов суждений в посылках
силлогизма. В сочетании по два (две посылки) четыре вида суждений (А, Е, I, О)
дадут шестнадцать вариаций:
| AA |
|
EA |
|
I A |
|
OA |
|
|
|
|
|
|
|
|
| AE |
|
EE |
|
I E |
|
OE |
|
|
|
|
|
|
|
|
| A I |
|
E I |
|
I I |
|
OI |
|
|
|
|
|
|
|
|
| AO |
|
EO |
|
I O |
|
OO |
Из
шестнадцати сочетаний не все могут дать правильные выводы. Модусы IА и АО
нарушают 2-е правило (средний термин не распределен в обеих посылках); модусы
АЕ, АО, IЕ не согласуются с 3-м правилом (больший термин должен быть
распределен в выводе, когда он не распределен в посылке); модусы II IО, ОI, ОО нарушают 4-е
правило (обе посылки частные); модусы ЕЕ, ЕО, ОЕ противоречат 6-му правилу (обе
посылки отрицательные).
Правильный
вывод дадут только 4 сочетания: АА, ЕА, АI, ЕI, выражающие правильные
модусы первой фигуры силлогизма. В первом модусе вывод общеутвердительный, во
втором – общеотрицательный, в третьем – частноутвердительный и в четвертом –
частноотрицательный. Символическое выражение модусов первой фигуры будет такое:
ААА, ЕАЕ, АII, ЕIО. Каждый из них имеет свое мнемоническое (греч. mnemonika – искусство запоминания)
название: Barbara, Celarent, Darii, Ferio. Гласные буквы в этих латинских названиях последовательно
выражают символ основных видов суждений, составляющих посылки и вывод
силлогизма.
Аналогичным
путем можно вывести правильные модусы второй и третьей фигуры. По второй фигуре
получим четыре модуса: ЕАЕ, АЕЕ, ЕIО, АОО. Третья фигура имеет шесть модусов:
ААI, IАI, АII, ЕАО, ОАО, ЕIО.
В качестве
примеров каждого модуса первой фигуры можно привести следующие силлогизмы:
Первый модус
(Barbara): «Регулярные физические
упражнения по утрам способствуют укреплению здоровья. Студент Андреев регулярно
делает утреннюю зарядку. Студент Андреев способствует укреплению своего
здоровья». (Рис. 7).
Рис. 7
Второй модус
(Celarent): «Вредные привычки
наносят вред здоровью. Курение – вредная привычка. Курение несовместимо с
крепким здоровьем». (Рис. 8).
Рис. 8
Третий модус
(Darii): «Все спортсмены
участвуют в соревнованиях. Некоторые сотрудники ХНУРЭ – спортсмены. Некоторые
сотрудники ХНУРЭ участвуют в соревнованиях». (Рис. 9).
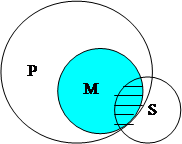
  Рис. 9 Рис. 9
Четвертый
модус (Ferio): «Ни одно растение не может существовать без фотосинтеза
органических веществ. Некоторые организмы – растения. Некоторые организмы не
могут существовать без фотосинтеза органических веществ». (Рис. 10).
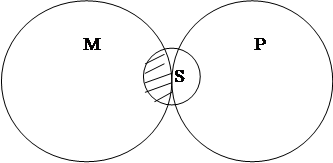
Рис. 10
Первая фигура
силлогизма наиболее типична для дедуктивного умозаключения, особенно ее первый
модус ААА. Модусы первой фигуры дают выводы всех видов суждения. Особую
ценность имеет общеутвердительный вывод, которого не может дать никакая иная
фигура силлогизма. В умозаключениях по этой фигуре наиболее ярко раскрывается
аксиома силлогизма, правильность вывода здесь легко проверить. Поэтому выводы
по другим фигурам стараются обычно свести к модусам первой фигуры
силлогистического умозаключения.
6. Сокращенные и сложные силлогизмы
Предложение с
выраженными в нем двумя частями силлогизма может представлять сокращенное
умозаключение. Такой сокращенный силлогизм называется энтимема (греч. enthymema) – неполно, сокращенно
приведенный аргумент, отсутствующие части которого подразумеваются очевидными.
Чаще всего опускается большая посылка как наиболее легко подразумеваемая и
высказывается только меньшая посылка и заключение. Например: «Алюминий – металл»,
говорит некто, имея в виду то, что алюминий проводник. Эта аргументация подлежит
проверке с целью выяснить ее корректность. Для этого надо выяснить, что
пропущено в аргументации: заключение или посылка (какая именно). Это можно
сделать, если мы найдем формальные показатели наличия следования; таковыми
являются слова и словосочетания «отсюда следует», «поэтому», «потому что»,
«ибо», «так как» и др. В нашем примере видно, что мы имеем дело с заключением,
где термин «алюминий» – меньший, а термин «металл» – больший. Но тогда
предложение «Алюминий – металл» – это меньшая посылки, где «проводник» – средний
термин. Теперь можно попытаться восстановить полный модус следующим образом:
«Всякий проводник – металл. Алюминий – проводник. Следовательно, алюминий – металл».
Сложный
силлогизм (полисиллогизм) – это сцепление ряда силлогизмов таким образом, что
заключение одного становится посылкой другого силлогизма и т.д. Всякое научное
мышление в развернутой или скрытой форме представляет собой полисиллогизм,
вытекающий из целой системы умозаключений.
Отличают
особый вид сложного силлогизма – сорит, состоящий из сокращенных силлогизмов. В
сорите приводится только последнее заключение, а все промежуточные опускаются.
Общая формула сорита такова: А-В, В-С, С-Д, следовательно, А-Д. Видно, что
здесь прослеживается стойкая цепь причин и следствий, от чего обоснованность
вывода усиливается, он становится особенно убедительным.
Сложно-сокращенный
силлогизм, в котором посылками служат энтимемы, называется эпихейрема. Схема
эпихейремы такова:
| М есть (не есть) Р, так как она есть (не есть) N, |
| S есть М, так
как оно есть О |
| S есть (не
есть) Р. |
Например:
| Ни одна птица не примат, так как ни одна птица не
млекопитающее. |
| Данные особи – птицы, так как они имеют перьевой покров. |
| Данные особи не приматы. |
Каждая
эпихейрема может быть превращена в сорит, если ее посылки превратить в полные
силлогизмы и расположить их определенным образом.
7. Условные,
разделительные и условно-разделительные силлогизмы
Условные
силлогизмы – такие, в которых либо одна, либо обе посылки – условные суждения.
Схема условного силлогизма, в котором обе посылки – условные суждения:
| Если А, то В |
|
| Если В, то С |
|
| Следовательно, если А, то С. |
Пример:
| Если тело подвергается трению, то оно нагревается. |
| Если тело нагревается, то оно расширяется. |
| Если тело подвергается трению, то оно расширяется. |
Аксиому чисто
условного силлогизма часто выражают словами: следствие следствия есть следствие
основания.
Условные
силлогизмы могут составлять целые цепи.
Условно-категорическими
называют такие умозаключения, одна из посылок которых является условным
суждением, а другая – суждением категорическим. Вывод в таких умозаключениях
представляет собой категорическое суждение. В условно-категорических
силлогизмах имеется два правильных модуса: модус ponens (или конструктивный),
другой – модус tollens (или деструктивный).
Модус ponens образует заключение от
согласия с основанием условной посылки к необходимости соглашаться и с ее
следствием. Форма этого модуса такова:
Модус tollens является умозаключением
от отрицания следствия условной посылки к отрицанию ее основания. Форма его
такая:
| Если А, то В. |
| Не В. |
| Не А. |
Абстрактно
рассуждая, можно сконструировать еще два вида сочетания посылок:
| 1) |
Если А, то В |
2) |
Если А, то В |
|
|
В |
|
Не А |
|
|
? |
|
? |
Но
определенного вывода в этих случаях сделать невозможно, если большая посылка
представляет собой обычное, не выделяющееся суждение. Например:
| 1) |
Если дождь идет, то на улице мокро; |
|
|
На улице мокро… |
|
|
? |
На улице
может быть мокро и без дождя, по другим причинам: растаял снег, проехала поливальная
машина и т.д. Основная причина невозможности вывода по этой форме кроется в так
называемой множественности причин. Чтобы вывод был верен, для следствия должна
существовать только одна причина, но это уже будет преобразованная форма с
включением в рассуждение знания об этой единственной причине.
На примере с
дождем и мокрой мостовой очевидна невозможность достоверного заключения во
втором виде сочетания посылок:
Разделительные
силлогизмы.
Разделительными,
или дизъюнктивными, силлогизмами называются такие, первая посылка которых есть
разделительное (дизъюнктивное) суждение. Вторая и вывод суть суждения
разделительные или категорические.
Схема
дизъюнктивного суждения, образующего первую посылку дизъюнктивного силлогизма,
имеет такой вид: S есть или А, или В, или С. Каждое из суждений, входящее в
данное разделительное суждение (S есть А; S есть В; S есть С), называются альтернативой. В нашем суждении
содержится три альтернативы.
Дизъюнктивные
силлогизмы имеют два модуса:
| а) |
S есть А, или
В, или С; |
|
|
S не есть ни
А, ни В |
|
|
Следовательно, S
есть С |
В этом модусе
во второй посылке отрицается все, кроме одной альтернативы, поэтому в выводе
утверждается эта оставшаяся альтернатива. Так как в выводе мы приходим к
утверждению, модус называется утверждающим, но путь наш состоял в отрицании
всех других альтернатив, кроме одной, то модус получил название модуса,
утверждающего посредством отрицания (tollendo ponens).
| б) |
S есть или А,
или В, или С; |
|
|
S есть А. |
|
|
Следовательно, S не есть ни В, ни С. |
В этом модусе
во второй посылке утверждается одна альтернатива; поэтому в выводе все
оставшиеся альтернативы отрицаются. Этот модус по своему итогу оказывается
отрицающим, а способ получения этого отрицания у него – утверждение. Поэтому
полное наименование этого модуса – модус, отрицающий посредством утверждения (ponendo tollens).
Для
правильного построения разделительного силлогизма и истинности вывода,
необходимо соблюдение следующих двух правил:
а) в
разделительном суждении должны быть приведены все возможные альтернативы.
Другими словами, деление субъекта суждения должно быть полным, исчерпывающим;
б) необходимо
учитывать точное значение союза «или», которое может быть и чисто
разделительным, и соединительно-разделительным, так как при чисто
разделительном значении «или» все альтернативы исключают одна другую, а при
соединительно-разделительном значении союза «или» альтернативы не исключают
одна другую.
Условно-разделительные
силлогизмы.
В
условно-разделительном (лемматическом) силлогизме одна посылка является
условным суждением, а вторая – разделительным. В зависимости от количества
альтернатив, содержащихся в разделительном суждении этого силлогизма, он
называется дилеммой, трилеммой, тетралеммой. Наиболее употребительной в
практике мышления является дилемма. Она бывает простой и сложной,
конструктивной (созидательной) и деструктивной (разрушительной).
В
конструктивной дилемме совершается мысленный переход от утверждения альтернатив
в основаниях условного суждения к утверждению соответствующих следствий. В
деструктивной дилемме происходит переход мысли от отрицания следствий к
отрицанию оснований.
Различия
между простой и сложной конструктивными дилеммами состоит в том, что: 1) в
большей посылке простой дилеммы каждое из двух оснований обусловливает одно и
то же следствие, а в сложной дилемме разные основания обусловливают разные
следствия; 2) в простой дилемме заключение является категорическим суждением, а
в сложной – разделительным.
Простая
конструктивная дилемма соответствует схеме:
| Если А, то С; если В, то С. |
| А или В. |
| С. |
Пример:
| Если число делится на 6, то оно делится на 2; |
| Если число делится на 8, то оно делится на 2. |
| Но данное число делится или на 6, или на 8. |
| Данное число делится на 2. |
Схема сложной
конструктивной дилеммы:
| Если А, то В; если С, то Д. |
| А или С. |
| В или Д. |
Пример:
Человек, находящийся в горящем доме, может рассуждать так:
| Если я пойду из дома по лестнице, то получу ожоги; если я |
| выпрыгну из окна, то получу ушибы. |
| Но я могу выпрыгнуть из окна или пойти по лестнице. |
| Я или получу ожоги, или получу ушибы. |
Простая и
сложная деструктивные дилеммы различаются тем, что: а) в большей посылке
простой дилеммы два возможных следствия вытекают из одного основания, а в
сложной – из двух оснований; б) заключение в простой деструктивной дилемме
является категорическим суждением, а в сложной – соединительным.
Схема простой
деструктивной дилеммы такова:
| Если А, то или В, или С. |
| Но не В и не С. |
| Не А. |
Пример:
| Если растение является деревом, то оно либо лиственное, |
| либо хвойное. |
| Но данное растение не есть ни лиственное и ни хвойное. |
| Данное растение не есть дерево. |
Схема сложной
деструктивной дилеммы:
| Если А, то В; если С, то Д. |
| Но не В и не Д. |
| Не А и не С. |
Пример:
| Если треугольник прямоугольный, то в нем есть два угла,
сумма которых равна одному прямому углу; если же треугольник тупоугольный, то
в нем есть два угла, сумма которых меньше прямого угла. |
| В данном треугольнике или нет двух углов, сумма которых
равна прямому углу, или нет двух углов, сумма которых меньше прямого угла. |
| Следовательно, данный треугольник и не прямоугольный, и
не тупоугольный. |
Правила
построения условно-разделительных силлогизмов таковы:
1. умозаключать в
условно-разделительных силлогизмах можно от утверждения основания к утверждению
следствия и от отрицания следствия к отрицанию основания, но нельзя
умозаключать от утверждения следствия к утверждению основания и от отрицания
основания к отрицанию следствия;
2. во второй посылке,
которая есть разделительное суждение, должны быть полностью перечислены все
альтернативы;
3. необходимо, чтобы союз
«или» имел чисто разделительное значение, то есть чтобы альтернативы были чисто
исключающими друг друга.
Неправильность
лемматического умозаключения часто вызывается тем, что дилемма формулируется
там, где необходимо формулировать трилемму или тетралемму, так как дилемма в
этом случае не исчерпывает всех альтернатив. Пример подобной ошибки – следующее
рассуждение:
| Данный лес или лиственный, или хвойный. |
| Установлено, что данный лес не лиственный. |
| Данный лес хвойный. |
Ошибка
состоит в том, что не учтена третья возможность – возможность быть смешанным
лесом.
8. Индуктивные умозаключения
Дедуктивные умозаключения,
которые мы рассмотрели, не исчерпывают всей области умозаключений, хотя и
составляют наиболее разработанную логикой часть. Если поставить вопрос о том,
как формируется то общее, которое, как мы выяснили, составляет исходный пункт
дедукции, то мы неизбежно придем к индуктивным умозаключениям.
Индукцию (от
лат. inductio – наведение) понимают как метод исследования, целью которого
является анализ движения знания от единичного к общему суждению. Но индукция
выступает и как определенная логическая форма, то есть такая устойчивая связь
мыслимого содержания, в которой отражается и фиксируется восхождение мысли от
менее общих положений к более общим положениям. Далее мы будем касаться именно
этого аспекта индукции.
Познавательное
значение индукции в общем и целом было уже отмечено Аристотелем. Ее связь с
опытным наблюдением и возможность непосредственной проверки индуктивных
обобщений делают ее простым и доступным методом, по сравнению с дедукцией. Сам
же Аристотель отдавал предпочтение более строгому виду умозаключения, а именно
силлогистике.
Виды индуктивных умозаключений
Различают
индукцию полную, если посылки исчерпывают весь класс предметов, подлежащих
индуктивному обобщению, и неполную, если посылки не исчерпывают всего класса
предметов, подлежащих индуктивному обобщению. Выводом как по полной, так и
неполной индукции является общее суждение.
Полная
индукция.
Ход мысли
осуществляется здесь по схеме:
S1 есть Р
S2 есть Р
………….
Sn есть Р
Известно, что
S1, S2 … Sn исчерпывают все предметы
класса. Следовательно, все S есть Р.
Например:
| Старший сын в семье Ивановых, Петя, ходит в школу. |
| Средний сын в семье Ивановых, Кирилл, ходит в школу. |
| Их младшая сестра Катя ходит в школу. |
| Петя, Кирилл и Катя – дети в семье Ивановых. |
| Следовательно, все дети семьи Ивановых посещают школу. |
Из этого
примера видно, что общий вывод основан на знании всей совокупности предметов
изучаемого класса (мы говорим о всех детях семьи Ивановых) и общий вывод
представляет собой категорическое суждение, где предикат посылок и вывода
(ходят в школу) один и тот же, как и вообще во всех индуктивных умозаключениях.
Но полная индукция
не дает знания о других предметах, кроме тех, которые берутся в качестве
частных посылок. Эти предметы она характеризует со стороны их родовой
принадлежность, и в этом следует усматривать новизну знания, которое индукция
порождает. Не будем упускать из вида, что именно знание такого рода лежит в
основе дедукции.
Однако в
реальном человеческом познании индукция занимает незначительное место, так как
с полным набором случаев человек в силу ограниченности своего бытия в
пространстве и времени, как правило, дела не имеет. Поэтому человеческое
мышление обращается к неполной индукции, в которой общий вывод делают на
основании знания не о всех предметах класса, а о некоторой части их. Основанием
для переноса знаний от части предметов на весь класс их служит внутренняя
природа самих вещей и общественно-историческая практика.
Обнаружив
сходство либо различие и установив что-либо относительно частных, принадлежащих
части класса случаев, человек затем это сходство (различие) переносит на весь
класс. Так поступают и в «житейских» ситуациях, и в науке. Многократная
практика подтверждает этот перенос и поэтому индукция позволяет сделать более
или менее правильный вывод. При этом непременным условием неполной индукции
(как и всех индуктивных заключений) является отсутствие противоречивых случаев.
Примером неполной индукции через простое перечисление при отсутствии
противоречивых случаев может служить следующий ход мысли:
| Железо – твердое тело; |
| Медь – твердое тело; |
| Золото – твердое тело; |
| Платина – твердое тело. |
| Следовательно, все металлы – твердые тела. |
Легко видеть,
что схема, по которой осуществляется вывод по неполной индукции, такова:
|
S1
есть Р
|
|
S2 есть Р
|
| …………. |
|
Sn есть Р
|
|
S1, S2 …, Sn –
часть класса S
|
| Следовательно, все S есть Р. |
Поскольку
вывод по неполной индукции есть скачек, переход от известного к неизвестному и
поскольку неполной индукцией сознательно вводится принцип рассмотрения не всего
количества предметов, а лишь части из них, постольку выводы по неполной
индукции всегда носят вероятностный характер. В силу этого опасность
заблуждения при индуктивном умозаключении больше, чем в силлогизме. Если в
силлогизме истинность вывода зависит от истинности посылок и соблюдения
определенных правил вывода, что само по себе является внешним условием по отношению
к самому силлогизму, то в неполной индукции сам скачек несет в себе возможность
ошибки, ибо достаточно одного противоречивого случая, чтобы все здание
индуктивного умозаключения рухнуло.
Например, все
учебники логики описывают ситуацию с лебедями на основании неполной индукции;
вывод «Все лебеди белые» был опровергнут, когда в Австралии впервые были
обнаружены черные лебеди. Или, в нашем предыдущем примере с металлами, мы
обнаруживаем, что ртуть (металл) не есть твердое тело, поэтому сделанный вывод
оказывается ложным.
Каковы же те
условия, которые повышают вероятность выводов по неполной индукции?
1) необходимо брать возможно
большее количество случаев для индуктивного обобщения. Например, когда более
вероятен вывод о том, что существует внеземная жизнь? В случае, если изучена
одна планета солнечной системы или если изучены несколько планет солнечной
системы? Последний случай, очевидно, предпочтительней;
2) вывод будет более
вероятен, когда факты, служащие основанием обобщения, более разнообразны и по
возможности более полно характеризуют предмет индуктивного обобщения. Это
относится и к предыдущему примеру;
3) вероятность вывода
повышается, если предметы, знания о которых индуктивно обобщаются, обладают
внутренней объективной связью между собой и чем более существенный признак
берется в качестве основы для обобщения.
Для
того, чтобы повысить качество выводов по неполной индукции, следует избегать
следующих ошибок:
1) «поспешное
обобщение». Оно происходит, если в посылках не учтены все обстоятельства,
которые, возможно, и являются причиной исследуемого явления. В определенной
степени это можно отнести к предсказаниям скорого наступления эры «машинного
мышления», которое (предсказание) очевидно основано на поверхностном обобщении
работы мозга и ЭВМ;
2) следует
избегать ошибки, называемой «после этого, значит, по причине этого» (post hoc, ergo propter hoc); об этом говорилось
выше.
Научная
индукция отличается от неполной индукции через простое перечисление при
отсутствии противоречащего случая (такую индукцию называют популярной, так как
посылки в ней нередко берутся случайно) тем, что она нацелена на отыскание
причинных связей, открытие законов. Поэтому научная индукция основывается на
таких методах познания, как наблюдение и эксперимент.
|