Курсовая работа: Сечение многогранников
Курсовая работа: Сечение многогранников
Министерство общего и
профессионального образования Российской Федерации
Калужский Государственный
Педагогический Университет
им. К.Э. Циолковского
Физико-математический
факультет
Кафедра алгебры и
информатики
Курсовая работа
Тема:
«Сечение многогранников»
Выполнил: студент IV
курса
физико-математического
факультета
Мосин Евгений Валерьевич.
Научный руководитель:
Булычев В.А.
Калуга 2006г.
Содержание
Введение
Глава I. Пространственные
тела и их сечения
1.1 Точка, прямая и
плоскость в пространстве. Векторы
1.2 Преобразования
пространства
1.3 Пространственные тела
1.4 Поверхности
второго порядка
Глава II. Изучение
сечений пространственных тел
2.1 Методы построения
сечений многогранников
2.2 Задание сечений
пространственных тел
2.3 Построение сечений
пространственных тел. Алгоритм
2.4 Исследование свойств
сечения
Глава III. Визуализация
3.1 Способы
визуализации трехмерного пространства
3.2 Перекрытие
3.3 Освещенность
Глава IV. Создание
компьютерного приложения.
4.1 Постановка требований
к реализуемому проекту
4.2 Разработка интерфейса
программы
4.2.1 Окна проекций
4.2.2 Меню пользователя
4.2.3 Основные методы
работы
4.2.4 Диалог просмотра
сечения
Заключение
Приложение
Список литературы
Введение
Важнейшей
задачей педагогической науки является совершенствование планирования процесса
обучения в целом и повышение эффективности управления познавательной
деятельностью учащихся.
Поиски
оптимальных путей управления обучением вылились в создание новой системы
учебной работы, названной программированным обучением, одними из составляющих
которого являются наглядность и интерактивность обучающих программ. В настоящей
курсовой работе мы рассмотрим возможность применения программированного
обучения при изучении стереометрии, а именно сечения пространственных тел.
Но прежде всего
необходимо отметить актуальность проблемы применения программированного (компьютерного)
обучения.
В настоящее
время наука и техника развиваются настолько быстро, что своевременное обобщение
потока научной информации без применения кибернетических средств, представляет
значительную трудность.
Не менее сложным
является сообщение учащимся знаний, так как их объем из года в год
увеличивается, тогда как сроки и методы обучения остаются неизменными. В связи
с этим все большее число преподавателей приходит к выводу о недостаточности
традиционных способов обучения и необходимости их совершенствования на основе
новейших достижений науки и техники.
В школах уже
появились компьютеры, но этого недостаточно. Самый лучший вариант – оснастить
подобным оборудованием каждый кабинет и включить элементы работы на компьютере
в учебные программы по всем предметам. Но для этого необходима техническая
база. Особо надо отметить содержание самих обучающих программ, применение
которых должно быть эффективным, а для этого необходимо разработать
дидактический материал с учетом психолого-педагогических особенностей обучения
геометрии.
В настоящее
время возможно использовать элементы программированного обучения в курсе
геометрии, так как большинство способов решения задач требует наглядного
представления, которое можно реализовать с помощью обучающих программ. Для
развития у школьников стереометрического (пространственного) представления,
плоских чертежей, представляющих собой проективное изображение пространственных
фигур, недостаточно необходимо создать инструмент, позволяющий интерактивно
изучать стереометрию. В данном проекте мы остановимся на теме сечения
пространственных тел.
Задачи
проекта:
1.
Изучение
теоретического материала по теме проекта;
2.
Создание
компьютерного приложения позволяющего изучать сечения пространственных тел;
3.
Оценка
проделанной работы и выявление дальнейших путей развития данной темы.
Основная цель
проекта: создание инструмента, позволяющего наглядно и интерактивно изучать
пространственные тела и их сечения.
Промежуточные
цели:
1.
Разработать
способ представления пространственных тел в памяти компьютера.
2.
Разработать
способ визуализации пространственных тел.
3.
Создать
алгоритм построения сечения пространственных тел.
4.
Рассмотреть
использование и реализацию интерактивности создаваемого приложения.
5.
Разработка
удобного, простого в обращении и достаточного полного интерфейса, создаваемого
компьютерного приложения.
Программное
обеспечение: среда программирования Delphi 7, текстовые редакторы Блокнот и MS
Word, графический редактор Paint.
Глава I. Пространственные
тела
1.1 Точка,
прямая и плоскость в пространстве. Векторы
Понятие точка
является определяющим понятием пространства, любая фигура пространства состоит
из множества точек. Хранение в памяти компьютера информации о элементах
пространства будем осуществлять с помощью хранения координат точек определяющих
данный элемент пространства. Так для хранения информации о прямой достаточно
всего двух различных точек принадлежащих этой прямой. По двум точкам задающим
прямую можно составить каноническое уравнение прямой и далее оперировать этим
уравнением:
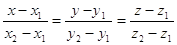 , (1′) , (1′)
где точки 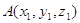 и и 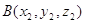 принадлежат
данной прямой. Или если использовать вектор принадлежат
данной прямой. Или если использовать вектор 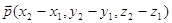 т.е. т.е. 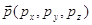 , получим следующее уравнение
прямой: , получим следующее уравнение
прямой:
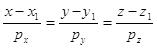 . (1′′) . (1′′)
Аналогично
прямой, плоскость определяется тремя точками:
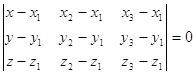 , (2′) , (2′)
где точки 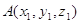 , , 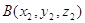 , , 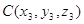 принадлежат
данной плоскости из этой матрицы можно получить уравнение плоскости: принадлежат
данной плоскости из этой матрицы можно получить уравнение плоскости:
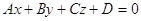 , (2′′) , (2′′)
где
коэффициенты 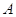 , ,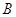 , ,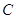 , ,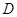 определяются следующим способом: определяются следующим способом:
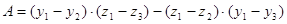 ; ;
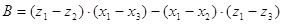 ; ;
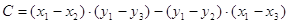 ; ;
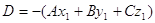 . .
Причем из
этих формул полезно знать, что координатами вектора нормального к данной
плоскости являются соответственно коэффициенты 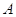 , ,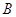 , ,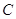 . Этот вектор направлен в
полупространство правого обхода точек. . Этот вектор направлен в
полупространство правого обхода точек.
Решая совместно
уравнения (1′′) и (2′′) найдем координаты точки пересечения
прямой и плоскости, при условии, что прямая пересекает плоскость. Пусть
плоскость задана тремя точками: 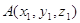 , , 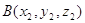 , , 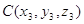 , а прямая задана двумя точками: , а прямая задана двумя точками: 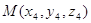 и и 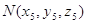 , тогда
координаты точки пересечения , тогда
координаты точки пересечения 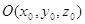 находятся по формулам: находятся по формулам:
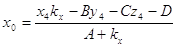 , ,
где 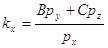 , причем если , причем если 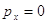 , то , то 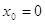 ; (1x) ; (1x)
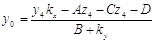 , ,
где 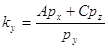 , причем если , причем если 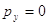 , то , то 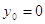 ; (1y) ; (1y)
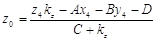 , ,
где 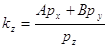 , причем если , причем если 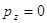 , то , то 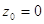 . (1z) . (1z)
В этих
формулах координаты вектора 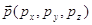 для прямой вычисляется следующим
образом: для прямой вычисляется следующим
образом: 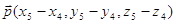 . .
1.2
Преобразования пространства
Для
реализации интерактивности изучения пространственных тел необходимо реализовать
возможность перемещения, поворота и масштабирования, а для этого необходимо
изменять координаты точек фигур по соответствующему закону. Рассмотрим три
преобразования которые переводят каждую точку 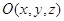 в точку в точку 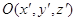 : :
1.
Перемещение
(параллельный перенос на вектор 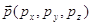 ). ).
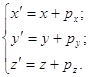 (1p) (1p)
2.
Поворот
вокруг прямой на угол 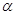 . Поворот будем осуществлять
вокруг одной из осей координат. . Поворот будем осуществлять
вокруг одной из осей координат.
а) вокруг оси
OX:
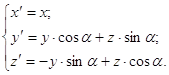 (2px) (2px)
б) вокруг оси
OY:
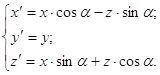 (2py) (2py)
в) вокруг оси
OZ:
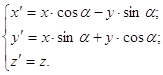 (2pz) (2pz)
3.
Масштабирование
с коэффициентом 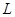 . .
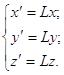 (3p) (3p)
1.3 Пространственные
тела
Как уже
говорилось, в памяти компьютера пространственные тела будем хранить в виде
координат точек определяющих эти тела. Рассмотрим далее, как хранить те или
иные виды пространственных тел и рассмотрим основные способы создания фигур. При
описании многогранников необходимо задание координат всех вершин
многогранников, а также описание порядка обхода каждой грани. Удобно описывать
обход граней почасовой стрелке наблюдая многогранник из вне, тогда нормальный
вектор к грани, заданный тройкой следующих подряд вершин, будет направлен из
многогранника. Это свойство удобно использовать при визуализации выпуклых
многогранников, об этом будет рассказано позднее. С многогранниками все
понятно, а как описывать поверхности второго порядка (поверхности вращения, конические
поверхности, цилиндрические поверхности, эллипсоид, гиперболоид, параболоид).
Их можно представить в виде многогранника с большим количеством граней, и чем
больше количество граней, тем точнее приближение. Этот метод является
универсальным, он позволяет описывать комбинированные пространственные тела, но
не позволяет изучать алгебраические кривые, которые получаются при построении
сечений. Приведем общую структуру файла, описывающего многогранник. Файл
представляет собой обычный текстовый документ.
Количество вершин многогранника.
Координаты 1й вершины через пробел.
Координаты 2й вершины через пробел.
Количество граней многогранника.
Порядок обхода 1й грани через пробел.
Порядок обхода 2й грани через пробел.
Пример
описания куба с ребром равным 2.
|
8
0 0 2
2 0 2
2 2 2
0 2 2
0 0 0
2 0 0
2 2 0
0 2 0
6
1 5 8 4
2 3 7 6
5 6 7 8
4 3 2 1
3 4 8 7
2 6 5 1
|
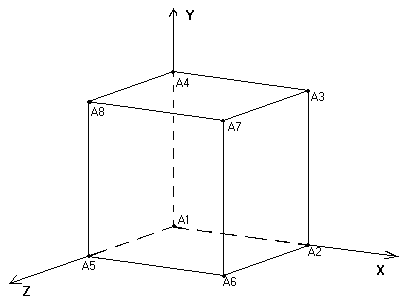
|
1.4 Поверхности
второго порядка
| № |
Название. |
Способ описания. |
| 1. |
Конус |
Как пирамида с большим числом вершин, в
основании которой лежит правильный многоугольник. |
| 2. |
Цилиндр |
Как призма с большим числом вершин,
основаниями которой являются правильные многоугольники. |
| 3. |
Сфера |
Многогранник, описанный по принципу
параллелей и меридианов. |
| 4. |
Тор |
Совокупность косоугольных цилиндров. |
Пример1: Методов
получения координат точек сферы.
|
for iy:=0 to ny-1 do
for ix:=0 to nx do
begin
x:=r*sin(iy*pi/ny)*cos(2*ix*pi/nx);
y:=r*sin(iy*pi/ny)*sin(2*ix*pi/nx);
z:=r*cos(iy*pi/ny);
x:=r*sin((iy+1)*pi/ny)*cos(2*ix*pi/nx);
y:=r*sin((iy+1)*pi/ny)*sin(2*ix*pi/nx);
z:=r*cos((iy+1)*pi/ny);
end;
|

|
Глава II.
Изучение сечений пространственных тел
2.1
Методы построения сечений многогранников
Геометрические
задачи традиционно делятся на три типа:
1)
на
вычисление;
2)
на
доказательство;
3)
на
построение.
Решение
любых стереометрических задач требует не только вычислительных и логических
умений и навыков, но и умений изображать пространственные фигуры на плоскости
(например, на листе бумаги, классной доске), что по сути своей тесно связано с
темой «Геометрические построения на плоскости». Стереометрические задачи на
вычисления и доказательство легко можно решать, используя правильный рисунок
пространственной фигуры. При изучении тем «Параллельность прямых и плоскостей в
пространстве», «Перпендикулярность прямых и плоскостей», «Углы между прямой и
плоскостью, между двумя прямыми, между двумя плоскостями» и других тем
прекрасным иллюстрационным материалом является решение позиционных и
метрических задач на построение пространственных фигур и сечений этих фигур
плоскостями. Основными методами построения сечений многогранников являются
следующие методы:
1.
Метод
следов. Суть метода заключается в построении вспомогательной прямой, являющейся
изображением линии пересечения секущей плоскости с плоскостью какой-либо грани
фигуры. Удобнее всего строить изображение линии пересечения секущей плоскости с
плоскостью нижнего основания. Эту линию называют следом секущей плоскости.
Используя след, легко построить изображения точек секущей плоскости,
находящихся на боковых ребрах или гранях фигуры. Последовательно соединяя
образы этих точек, получим изображение искомого сечения.
2.
Метод
вспомогательных сечений. Этот метод построения сечений многогранников является
в достаточной мере универсальным. В тех случаях, когда нужный след (или следы)
секущей плоскости оказывается за пределами чертежа, этот метод имеет даже
определенные преимущества. Вместе с тем следует иметь в виду, что построения,
выполняемые при использовании этого метода, зачастую получаются «скученными».
Тем не менее, в некоторых случаях метод вспомогательных сечений оказывается
наиболее рациональным.
3.
Комбинированный
метод построения сечений. Суть комбинированного метода построения сечений
многогранников состоит в применении теорем о параллельности прямых и плоскостей
в пространстве в сочетании с методом следов и методом вспомогательных сечений.
4.
Координатный
метод построения сечений. Суть координатного метода заключается в вычислении
координат точек пересечения ребер или многогранника с секущей плоскостью,
которая задается уравнением плоскости. Уравнение плоскости сечения вычисляется
на основе условий задачи.
Из
всех перечисленных способов построения сечения наиболее приемлемым является
координатный метод, так как он связан с большим объемом вычислений и имеет
простой алгоритм реализации, что целесообразно реализовать с помощью ЭВМ.
Достаточно знать координаты вершин каждой грани многогранника и три точки
задающие плоскость сечения.
2.2
Задание сечений пространственных тел
Как
уже говорилось, удобнее всего задавать плоскость сечения тремя точками, причем
координаты этих точек должны быть известны или должны вычисляться. Рассмотрим
возможные варианты задания точек плоскости сечения:
1)
точка
расположена вне многогранника;
2)
точка
находится внутри многогранника;
3)
точка
расположена в грани многогранника;
4)
точка
принадлежит ребру многогранника;
5)
точка
принадлежит диагонали многогранника;
6)
точка
совпадает с вершиной многогранника.
Условие
задания секущей плоскости тремя точками будет выполняться не всегда и в этом
случае придется вычислять уравнение плоскости сечения, используя другие методы.
В данной работе рассматривается лишь способ задания тремя точками.
2.3 Построение
сечений пространственных тел. Алгоритм
Метод построения
сечения заключается в нахождении точек пересечения секущей плоскости с гранями
многогранника, а вернее с ребрами многогранника. Проверка на пересечение
секущей плоскости и ребра многогранника производится следующим образом:
1.
Составление
уравнения секущей плоскости по трем точкам;
2.
Подстановка
в уравнение координат концов ребра с целью проверки: расположены ли точки в
разных полупространствах относительно плоскости сечения.
3.
Нахождение
точки пересечения ребра многогранника и плоскости сечения.
Для каждой
грани записываются две точки, причем запись производится только для тех граней,
где плоскость сечения пересекла два ребра. Далее используя полученные данные,
строится многоугольник сечения следующим образом:
1.
Берем
первую пару точек и ищем следующую пару точек в которой повторяется одна из
точек первой пары.
2.
Найдя
следующую пару проделываем для нее тоже самое, что и для первой пары, но
исключаем из поиска первую пару.
3.
Проделываем
весь алгоритм для каждой пары, пока не останется одна ненайденная точка.
4.
Полученная
цепочка является последовательным описанием ребер многоугольника сечения.
Далее
запоминаем полученный многоугольник, как новую грань многогранника.
2.4 Исследование
свойств сечения
Перечислим
некоторые свойства сечения (исходя из факта, что сечением является
многоугольник).
1.
Уравнение
плоскости сечения.
2.
Количество
вершин многоугольника сечения.
3.
Площадь
многоугольника сечения.
4.
Координаты
вершин многоугольника сечения.
5.
Двугранный
угол между плоскостью сечения и гранями многогранника.
6.
Углы
при вершинах многоугольника сечения.
Некоторые из
этих свойств реализованы в программе (1,2,3,4).
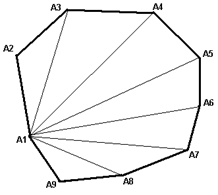
Пример:
Нахождение площади сечения. Так как строятся сечения выпуклых многогранников,
то многоугольник сечения будет тоже выпуклым, т.е. его площадь можно найти
разбиением на треугольники (площадь сечения равна сумме площадей треугольников
из которых оно составлено).
Глава III.
Визуализация
3.1 Способы
визуализации трехмерного пространства
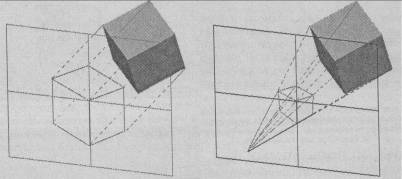
Для
визуализации используются два вида проекций: параллельные (аксонометрические)
(на рисунке слева) и центральные (перспективные)
(на рисунке
справа). При построении аксонометрической проекции пространственного тела его отдельные
точки сносятся на плоскость проекции параллельным пучком лучей, а при
построении центральной проекции – пучком лучей исходящих из одной точки,
соответствующей положению глаз наблюдателя. Частным случаем аксонометрической
проекции является проекция ортографическая, при построении которой плоскость
проекции выравнивается параллельно одной из координатных плоскостей.
3.2
Перекрытие
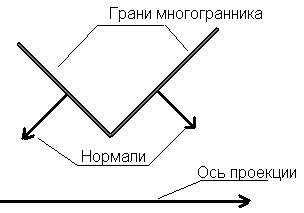
Под
перекрытием понимается тот факт, что невозможно одновременно видеть все грани
многогранника и какие - то грани обязательно окажутся невидимыми. Проблема
состоит в том, как узнать какие грани видны, а какие нет. В проекте мы
рассматриваем только выпуклые многогранники, поэтому для реализации перекрытия
используется тот факт, что нормальный вектор к каждой грани направлен извне.
Т.е. если использовать ортографическую проекцию, то тот факт, что координатная
составляющая (оси проекции) нормального вектора положительна, то грань видима,
если отрицательна, то грань перекрыта.
3.3
Освещенность
Освещенность
граней вычисляется путем, вычисления угла (синуса угла) между нормальным
вектором к грани и осью ортографической проекции.
Глава IV. Создание
компьютерного приложения
4.1 Постановка
требований к реализуемому проекту
1.
Простота
использования.
2.
Полнота
необходимых инструментов и возможностей.
3.
Интерактивность.
4.
Быстрота
работы.
5.
Простота
создания входного файла.
4.2 Разработка
интерфейса программы
При
разработке интерфейса программы уклон делался на стандартизацию меню и удобство
использования. Также необходима функция встроенных подсказок (всплывающих и в
строке состояния).
4.2.1 Окна
проекций
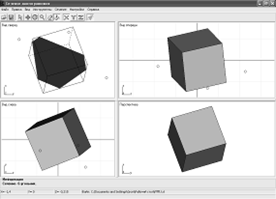
В программе
используются три окна проекции: вид сверху, вид слева, вид спереди,
перспектива. Размер окон проекции изменяется путем перемещения цента
разделителя. Также здесь показаны оси координат. Существует возможность
включения координатной сетки.
4.2.2 Меню
пользователя
Файл
Открыть
(загрузка файла многогранника).
Сохранить
(сохранение файла).
Выход (выход
из программы).
Правка
Сброс (сброс
всех измененных параметров).
Вид
Каркас
(отображаются ребра многогранника).
Заливка
(вывод граней, с расчетом их освещенности).
Обозначить
(обозначить вершины многогранника).
Сетка (вывод
сетки координат).
Инструменты
Выбрать
(позволяет выбирать и перемещать точки задающие сечение).
Переместить
(перемещение многогранника).
Повернуть
(поворот многогранника).
Масштаб
(масштаб окон проекций).
Стирка
(позволяет отключать заливку выбранной грани).
Заливка
(позволяет включить заливку выбранной грани).
Ограничить
(ограничение манипулирования сценой по осям координат).
Цент поворота
(изменение центра поворота).
Распространить
(изменять координаты точек задающих сечение вместе с координатами
многогранника).
Сечение
Построить
(построение сечения путем задания трех точек плоскости сечения).
Удалить
(удаление сечения).
Вид (настройка
вида сечения).
Привязать
(привязка выбранной точки сечения к элементам многогранника).
Просмотр
(окно просмотра сечения).
Настройка
Цвет (вызов
диалога изменения цветовой схемы)
4.2.3 Основные
методы работы
Основной
метод работы заключается в выборе инструмента, затем наведении курсора на
объект действия и манипуляция с помощью нажатия клавиши мыши.
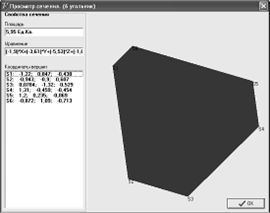
4.2.4 Диалог
просмотра сечения
Вывод
многоугольника сечения производится с помощью поворота плоскости сечения в
положение параллельности плоскости XOY.
Заключение
В заключении
данного проекта рассмотрим возможные пути дальнейшего развития проекта и его
использования, а также оценку выполнения поставленной задачи и отметим
полученные результаты. Поставленная перед началом работы цель: создание
инструмента, позволяющего наглядно и интерактивно изучать пространственные тела
и их сечения – реализована.
Создано
приложение, которое позволяет загружать пространственные тела и манипулировать
ими – это уже можно использовать при начальном изучении пространственных тел.
Далее в программе реализована функция построения сечения пространственных фигур
плоскостью, которая задается тремя точками, координаты которых можно изменять.
Минусом программы является возможность изучения только выпуклых фигур и
невозможность построения более одного сечения.
Пути
дальнейшего развития проекта:
1.
Построение
нескольких сечений;
2.
Возможность
загрузки невыпуклых фигур;
3.
Подбор
задач решаемых с помощью созданного приложения;
4.
Разработка
методик применения программы в обучении;
5.
Создание
конструктора пространственных тел;
6.
Создание
интерактивного инструмента для построения сечений пространственных фигур
аксиоматическим методом («Живая стереометрия»);
7.
Создание
обучающего модуля и методического сопровождения к нему;
8.
Применение
на практике.
Изучаемая в
данной курсовой работе тема, должна быть изучена до конца, так как это может
найти целесообразное и удачное применение на практике.
Приложение
Текст
программы
unit Unit1;
interface
uses
Windows, Messages,
SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, ComCtrls, Menus,
ExtCtrls, jpeg, ToolWin, StdCtrls, ImgList;
type
Point=record x,y,z:real
end; {координаты точки}
Vector=record x,y,z:real
end; {координаты ветора}
type
TForm1 = class(TForm)
StatusBar1: TStatusBar; StatusBar2:
TStatusBar; MainMenu1: TMainMenu;
N1: TMenuItem; N2:
TMenuItem; N3: TMenuItem; N4: TMenuItem; N5: TMenuItem; N6: TMenuItem;
N20: TMenuItem; N21:
TMenuItem; N22: TMenuItem; N18: TMenuItem; N25: TMenuItem; N30: TMenuItem;
N31: TMenuItem; N32:
TMenuItem; N33: TMenuItem; OD1: TOpenDialog; SD1: TSaveDialog;
PTop: TPanel; ITop:
TImage; PFront: TPanel; PLeft: TPanel; PPerspective: TPanel; IFront: TImage;
ILeft: TImage; IPerspective:
TImage; GroupBox1: TGroupBox; Vertikal: TPanel; Horizontal: TPanel; Panel3:
TPanel;
Centr: TPanel; ImList1:
TImageList; N23: TMenuItem; ToolBar1: TToolBar;
ToolButton1: TToolButton;
ToolButton2: TToolButton; ToolButton3: TToolButton; ToolButton4: TToolButton;
ToolButton5: TToolButton;
ToolButton6: TToolButton; ToolButton7: TToolButton; ToolButton8: TToolButton;
ToolButton9: TToolButton;
ToolButton10: TToolButton; ToolButton14: TToolButton; ToolButton19:
TToolButton;
ToolButton11:
TToolButton; ToolButton12: TToolButton; Label1: TLabel; ToolButton13:
TToolButton;
N26: TMenuItem; N27:
TMenuItem; N28: TMenuItem; N29: TMenuItem; N34: TMenuItem; N35: TMenuItem;
N36: TMenuItem; N37:
TMenuItem; N38: TMenuItem; N39: TMenuItem; N40: TMenuItem; N41: TMenuItem;
N42: TMenuItem; N43:
TMenuItem; N45: TMenuItem; N46: TMenuItem; N47: TMenuItem; N51: TMenuItem;
IntWiew: TMenuItem; N7:
TMenuItem; N8: TMenuItem; N9: TMenuItem; N10: TMenuItem; N11: TMenuItem;
N12: TMenuItem; N13:
TMenuItem; N14: TMenuItem; N15: TMenuItem; N16: TMenuItem; N17: TMenuItem;
N24: TMenuItem; N19:
TMenuItem; Mag1: TMenuItem; Mag2: TMenuItem; Mag3: TMenuItem;
procedure N5Click(Sender:
TObject);
procedure
CentrMouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
procedure
CentrMouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
procedure FormCreate(Sender:
TObject); procedure FormResize(Sender: TObject); procedure N2Click(Sender:
TObject);
procedure
ITopClick(Sender: TObject); procedure IFrontClick(Sender: TObject); procedure
ILeftClick(Sender: TObject);
procedure
ITopMouseMove(Sender: TObject; Shift: TShiftState; X, Y: Integer);
procedure
IFrontMouseMove(Sender: TObject; Shift: TShiftState; X, Y: Integer);
procedure
ILeftMouseMove(Sender: TObject; Shift: TShiftState; X, Y: Integer);
procedure N3Click(Sender:
TObject); procedure N33Click(Sender: TObject); procedure
ToolButton1Click(Sender: TObject); procedure ToolButton2Click(Sender: TObject);
procedure FormPaint(Sender: TObject);
procedure
ITopMouseDown(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
procedure
IFrontMouseDown(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
procedure
ILeftMouseDown(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
procedure
N25Click(Sender: TObject); procedure N21Click(Sender: TObject);
procedure
N22Click(Sender: TObject); procedure N8Click(Sender: TObject);
procedure
N16Click(Sender: TObject); procedure IntWiewClick(Sender: TObject);
procedure
N27Click(Sender: TObject); procedure N28Click(Sender: TObject);
procedure
N29Click(Sender: TObject); procedure N34Click(Sender: TObject);
procedure
N36Click(Sender: TObject); procedure N37Click(Sender: TObject);
procedure N9Click(Sender:
TObject); procedure N10Click(Sender: TObject);
procedure
IPerspectiveClick(Sender: TObject);
procedure
N41Click(Sender: TObject); procedure N14Click(Sender: TObject);
procedure
N18Click(Sender: TObject); procedure ToolButton4Click(Sender: TObject);
procedure
ToolButton5Click(Sender: TObject); procedure ToolButton6Click(Sender: TObject);
procedure
ToolButton7Click(Sender: TObject); procedure ToolButton8Click(Sender: TObject);
procedure
ToolButton9Click(Sender: TObject); procedure ToolButton12Click(Sender:
TObject);
procedure
ToolButton11Click(Sender: TObject); procedure ToolButton19Click(Sender:
TObject);
procedure
ToolButton13Click(Sender: TObject); procedure N24Click(Sender: TObject);
procedure
N19Click(Sender: TObject); Function Normal (A,B,C:Point):Vector;
procedure
Mag1Click(Sender: TObject); procedure Mag2Click(Sender: TObject);
procedure
Mag3Click(Sender: TObject);
private
{ Private declarations }
Procedure DrawGrane;
public
{ Public declarations }
end;
const
Gran=10000;{Максимум ганей}
Pointer=10000;{Максимум
вершин}
Lok=0.00001;{Погрешность
сечения}
SizeT=5;{Размер точек
сечения}
Sumbol='A';{Обозначение
точек}
type
TView=array [1..gran]of
record Visible:boolean;{Флаг активного окна}
Paint:boolean;
BrushGr:boolean;{Флаг
заливки грани}
PenRb:boolean;{Флаг
отрисовки ребер}
Intersection:boolean;{Флаг
наличия сечения}
ColorGr,ColorRb:TColor{Цвет:
грани,ребра} end;
TMainVar=record
Cx,Cy:integer; Mash:real;Net:boolean; end;
var
Form1: TForm1;
V:array[1..pointer]of
Point;{координаты вершин}
E:array[1..gran,0..pointer]of
integer;{грани [номер грани, номер вершины]}
Scene:array[1..4]of record
G:TView; M:TMainVar; Active:boolean; end;
M,N:word;{количество
граней, количество вершин}
X0,Y0,Num:integer;{координаты
щелчка мыши}
ActivColor,ColorEder,ColorUnEder,ColorRebro,ColorIntersection,ColorPointIntersection,ColorNet:TColor;{Цвет:
активного окна}
InterPoint:array[1..3]of
Point;
Count:byte;
kl:integer;
A,B,C,D,P1,P2,P3:real;
PanelWindow:array[1..4]of
TPanel;
WindowProection:array[1..4]of
TImage;
NameWindows:array[1..4]of
string=('Вид сверху','Вид спереди','Вид слева','Перспектива');{Название окон}
OsiX:array[1..4]of
string=('x','x','y','x');
OsiY:array[1..4]of
string=('z','y','x','z');
OsiZ:array[1..4]of
string=('y','z','z','y');
Magnit:array[1..3]of
TMenuItem;
MagPoint:array[1..3,1..2]of
Point;
First:array[1..3]of
boolean;
MPI:boolean;
implementation
uses Unit2,Unit3;
//Перевод вещественных
координат в экранные
Function Ser(win:byte;
T:Point; Main:TMainVar):TPoint;
var CopySer:Tpoint;
begin
case win of
1: begin
CopySer.X:=round(Main.Cx+(T.x*Main.Mash));
CopySer.Y:=round(Main.Cy-(T.y*Main.Mash))
end;
2: begin
CopySer.X:=round(Main.Cx+(T.x*Main.Mash));
CopySer.Y:=round(Main.Cy-(T.z*Main.Mash))
end;
3: begin
CopySer.X:=round(Main.Cx+(T.y*Main.Mash));
CopySer.Y:=round(Main.Cy-(T.z*Main.Mash))
end;
4: begin
CopySer.X:=round(Main.Cx+(T.x*Main.Mash));
CopySer.Y:=round(Main.Cy-(T.y*Main.Mash))
end;
end;
Ser:=CopySer
end;
Function UnSer(win:byte;
X,Y:integer;Tx,Ty,Tz:real; Main:TMainVar):Point;
var CopyUnSer:Point;
begin
case win of
1: begin
CopyUnSer.x:=(X-Main.Cx)/Main.Mash;
CopyUnSer.y:=(Main.Cy-Y)/Main.Mash;
CopyUnSer.z:=Tz end;
2: begin
CopyUnSer.x:=(X-Main.Cx)/Main.Mash;
CopyUnSer.y:=Ty;
CopyUnSer.z:=(Main.Cy-Y)/Main.Mash end;
3: begin CopyUnSer.x:=Tx;
CopyUnSer.y:=(X-Main.Cx)/Main.Mash;
CopyUnSer.z:=(Main.Cy-Y)/Main.Mash
end;
end;
UnSer:=CopyUnSer
end;
Procedure
TForm1.DrawGrane;
Procedure
GranBrush(Main:TMainVar; win:byte; i:integer; P:TPenStyle; var Can:TImage);
var j:integer;
w:array of TPoint;
begin
SetLength(w,E[i,0]);
for j:=1 to E[i,0] do
w[j-1]:=Ser(win,V[E[i,j]],Main);
if
Scene[win].G[i].BrushGr and Scene[win].G[i].Paint then
begin
Can.Canvas.Pen.Style:=psSolid;
Can.Canvas.Pen.Color:=Scene[win].G[i].ColorGr;
Can.Canvas.Brush.Color:=Scene[win].G[i].ColorGr;
Can.Canvas.Polygon(w);
end;
if Scene[win].G[i].PenRb
then
begin
Can.Canvas.Pen.Style:=P;
Can.Canvas.Pen.Color:=Scene[win].G[i].ColorRb;
Can.Canvas.Brush.Style:=bsClear;
Can.Canvas.MoveTo(w[0].X,w[0].Y);
for j:=1 to E[i,0]-1 do
Can.Canvas.LineTo(w[j].X,w[j].Y);
Can.Canvas.LineTo(w[0].X,w[0].Y);
end;
end;
//* Оси координат
Procedure
LineOs(i:byte;var Can:TImage);
var j,k,a,b:integer;
begin
Can.Canvas.Pen.Color:=ColorNet;
a:=round(Can.Width/Scene[i].M.Mash)
div 2;
b:=round(Can.Height/Scene[i].M.Mash)
div 2;
for j:=-a to a do
begin
Can.Canvas.MoveTo(Scene[i].M.Cx+round(j*Scene[i].M.Mash),0);
Can.Canvas.LineTo(Scene[i].M.Cx+round(j*Scene[i].M.Mash),Can.Height);
end;
for j:=-b to b do
begin
Can.Canvas.MoveTo(0,Scene[i].M.Cy+round(j*Scene[i].M.Mash));
Can.Canvas.LineTo(Can.Width,Scene[i].M.Cy+round(j*Scene[i].M.Mash));
end;
Can.Canvas.Pen.Color:=clBlack;
Can.Canvas.MoveTo(Scene[i].M.Cx,0);
Can.Canvas.LineTo(Scene[i].M.Cx,Can.Height);
Can.Canvas.MoveTo(0,Scene[i].M.Cy);
Can.Canvas.LineTo(Can.Width,Scene[i].M.Cy);
end;
// Система координат
Procedure
InpOboz(i,k:integer);
var j:integer;
A:TPoint;
s:string;
begin
WindowProection[k].Canvas.Pen.Color:=clBlack;
WindowProection[k].Canvas.Brush.Style:=bsClear;
WindowProection[k].Canvas.Font.Height:=8;
for j:=1 to E[i,0] do
begin
s:='';
A:=Ser(k,V[E[i,j]],Scene[k].M);
if Form1.N24.Checked then
s:=s+Sumbol+inttostr(E[i,j]);
if Form1.N19.Checked then
s:=s+'('+floattostrf(V[E[i,j]].x,ffGeneral,3,5)+';'+floattostrf(V[E[i,j]].y,ffGeneral,3,5)+';'+floattostrf(V[E[i,j]].z,ffGeneral,3,5)+')';
WindowProection[k].Canvas.TextOut(A.X,A.Y,s);
end;
end;
Procedure InpOsi(k:byte);
var i:integer;
begin
WindowProection[k].Canvas.Pen.Color:=clBlack;
WindowProection[k].Canvas.Brush.Style:=bsClear;
WindowProection[k].Canvas.MoveTo(10,WindowProection[k].Height-10);
WindowProection[k].Canvas.LineTo(10,WindowProection[k].Height-40);
WindowProection[k].Canvas.MoveTo(10,WindowProection[k].Height-10);
WindowProection[k].Canvas.LineTo(40,WindowProection[k].Height-10);
WindowProection[k].Canvas.Font.Height:=8;
WindowProection[k].Canvas.Font.Color:=clBlue;
WindowProection[k].Canvas.TextOut(12,WindowProection[k].Height-50,OsiX[K]);
WindowProection[k].Canvas.TextOut(12,WindowProection[k].Height-23,OsiY[K]);
WindowProection[k].Canvas.TextOut(40,WindowProection[k].Height-20,OsiZ[K]);
end;
var i,j:integer;
begin
for j:=1 to 4 do
begin
if Scene[j].M.Net then
LineOs(j,WindowProection[j]);
if Form1.IntWiew.Enabled
and Form1.N46.Checked then
GranBrush(Scene[j].M,j,M+1,psSolid,WindowProection[j]);
for i:=1 to M do
if (not
Scene[j].G[i].Visible) then
GranBrush(Scene[j].M,j,i,psDot,WindowProection[j]);
if Form1.IntWiew.Enabled
and Form1.N45.Checked then
GranBrush(Scene[j].M,j,M+1,psSolid,WindowProection[j]);
for i:=1 to M do
if Scene[j].G[i].Visible
then
GranBrush(Scene[j].M,j,i,psSolid,WindowProection[j]);
if Form1.N24.Checked or
Form1.N19.Checked then
for i:=1 to M do
if Scene[j].G[i].Visible
then
InpOboz(i,j);
WindowProection[j].Canvas.Brush.Style:=bsClear;
WindowProection[j].Canvas.Font.Height:=8;
WindowProection[j].Canvas.Font.Color:=clBlack;
WindowProection[j].Canvas.TextOut(1,1,NameWindows[j]);
InpOsi(j);
end;
end;
{$R *.dfm}
//* Активация окна
Procedure
ActivWindowProection(i:byte);
var j:byte;
begin
for j:=1 to 3 do
begin
PanelWindow[j].Color:=clBtnFace;
Scene[j].Active:=false
end;
PanelWindow[i].Color:=ActivColor;
Scene[i].Active:=true
end;
//* Полуплоскость
Function
SelectGran(i,x,y:integer):integer;
Function
Poluploscost(x1,y1,x2,y2,x,y:real):boolean;
begin
Poluploscost:=((x-x1)*(y2-y1)-((y-y1)*(x2-x1)))>0
end;
var j,k,l,rez:integer;
Inter:boolean;
begin
rez:=0; Inter:=true;
for k:=1 to M do
if Scene[i].G[k].Visible
then
begin
for j:=1 to E[k,0]-1 do
case i of
1: if
Poluploscost(V[E[k,j]].x,V[E[k,j]].y,V[E[k,j+1]].x,V[E[k,j+1]].y,(X-Scene[i].M.Cx)/Scene[i].M.Mash,(Scene[i].M.Cy-Y)/Scene[i].M.Mash)
then Inter:=false;
2: if not
Poluploscost(V[E[k,j]].x,V[E[k,j]].z,V[E[k,j+1]].x,V[E[k,j+1]].z,(X-Scene[i].M.Cx)/Scene[i].M.Mash,(Scene[i].M.Cy-Y)/Scene[i].M.Mash)
then Inter:=false;
3: if
Poluploscost(V[E[k,j]].y,V[E[k,j]].z,V[E[k,j+1]].y,V[E[k,j+1]].z,(X-Scene[i].M.Cx)/Scene[i].M.Mash,(Scene[i].M.Cy-Y)/Scene[i].M.Mash)
then Inter:=false;
end;
if Inter then
case i of
1: if
Poluploscost(V[E[k,E[k,0]]].x,V[E[k,E[k,0]]].y,V[E[k,1]].x,V[E[k,1]].y,(X-Scene[i].M.Cx)/Scene[i].M.Mash,(Scene[i].M.Cy-Y)/Scene[i].M.Mash)
then Inter:=false;
2: if not
Poluploscost(V[E[k,E[k,0]]].x,V[E[k,E[k,0]]].z,V[E[k,1]].x,V[E[k,1]].z,(X-Scene[i].M.Cx)/Scene[i].M.Mash,(Scene[i].M.Cy-Y)/Scene[i].M.Mash)
then Inter:=false;
3: if
Poluploscost(V[E[k,E[k,0]]].y,V[E[k,E[k,0]]].z,V[E[k,1]].y,V[E[k,1]].z,(X-Scene[i].M.Cx)/Scene[i].M.Mash,(Scene[i].M.Cy-Y)/Scene[i].M.Mash)
then Inter:=false;
end;
if Inter then
begin
rez:=k;
Break;
end
else
begin
rez:=0;
Inter:=true;
end;
end;
SelectGran:=rez;
end;
//* Выбор точек сечения
Procedure
MoveP(win,j,X,Y:integer);
Procedure
PNormal(P1,P2:Point;var M:Point);
var i:integer;
Li,No:Vector;
O:Point;
Q,P1O,P2O:real;
begin
Li.x:=P1.x-P2.x;
Li.y:=P1.y-P2.y;
Li.z:=P1.z-P2.z;
No.x:=M.x-P1.x;
No.y:=M.y-P1.y;
No.z:=M.z-P1.z;
Q:=sqr(Li.x)+sqr(Li.y)+sqr(Li.z);
O.x:=(Li.x*((Li.y*No.y)+(Li.z*No.z)+(Li.x*M.x))+(P1.x*(sqr(Li.y)+sqr(Li.z))))/Q;
O.y:=(Li.y*((Li.x*No.x)+(Li.z*No.z)+(Li.y*M.x))+(P1.y*(sqr(Li.x)+sqr(Li.z))))/Q;
O.z:=(Li.z*((Li.x*No.x)+(Li.y*No.y)+(Li.z*M.x))+(P1.z*(sqr(Li.x)+sqr(Li.y))))/Q;
P1O:=sqrt(sqr(O.x-P1.x)+sqr(O.y-P1.y)+sqr(O.z-P1.z));
P2O:=sqrt(sqr(O.x-P2.x)+sqr(O.y-P2.y)+sqr(O.z-P2.z));
if (P1O<>0) and
(P2O<>0) then
if
(sqrt(Q)/P1O<1)or(sqrt(Q)/P2O<1) then
if P1O/P2O<1 then
O:=P1 else O:=P2;
M:=O;
end;
begin
InterPoint[j]:=UnSer(win,X,Y,InterPoint[j].x,InterPoint[j].y,InterPoint[j].z,Scene[win].M);
if Magnit[j].Checked and
(not first[j]) then
PNormal(MagPoint[j,1],MagPoint[j,2],
InterPoint[j]);
Form1.StatusBar2.Panels[0].Text:='X=
'+floattostrf(InterPoint[j].x,ffGeneral,3,5);
Form1.StatusBar2.Panels[1].Text:='Y=
'+floattostrf(InterPoint[j].y,ffGeneral,3,5);
Form1.StatusBar2.Panels[2].Text:='Z=
'+floattostrf(InterPoint[j].z,ffGeneral,3,5);
end;
Procedure
SelectPointIntersection(i,x,y:integer;var Num:integer);
Function
SelP(X,Y,Xt,Yt,ST:real):boolean;
var Obl:boolean;
begin
Obl:=false;
if (X<(Xt+ST)) and
(X>(Xt-ST)) then
if (Y<(Yt+ST)) and
(Y>(Yt-ST)) then
Obl:=true;
SelP:=Obl;
end;
var j:integer;
begin
Num:=0;
for j:=1 to 3 do
case i of
1: if
SelP((X-Scene[i].M.Cx)/Scene[i].M.Mash,(Scene[i].M.Cy-Y)/Scene[i].M.Mash,InterPoint[j].x,InterPoint[j].y,SizeT/Scene[i].M.Mash)
then Num:=j;
2: if
SelP((X-Scene[i].M.Cx)/Scene[i].M.Mash,(Scene[i].M.Cy-Y)/Scene[i].M.Mash,InterPoint[j].x,InterPoint[j].z,SizeT/Scene[i].M.Mash)
then Num:=j;
3: if
SelP((X-Scene[i].M.Cx)/Scene[i].M.Mash,(Scene[i].M.Cy-Y)/Scene[i].M.Mash,InterPoint[j].y,InterPoint[j].z,SizeT/Scene[i].M.Mash)
then Num:=j;
end;
end;
Function
SelReber(win,x,y:integer;var ds:TPoint):boolean;
var rez:boolean;
Function LinEx(i:integer;
x1,y1,x2,y2,x,y:real):boolean;
begin
LinEx:=abs(round(((x-x1)*(y2-y1)-((y-y1)*(x2-x1)))*Scene[i].M.Mash))<5
end;
Procedure
FindRb(ind1,ind2:integer);
begin
ds.x:=ind1;
ds.y:=ind2;
rez:=true;
end;
var j,k:integer;
begin
rez:=false;
for j:=1 to M do
if
Scene[win].G[j].Visible then
begin
for k:=1 to E[j,0]-1 do
begin
case win of
1: if
LinEx(win,V[E[j,k]].x,V[E[j,k]].y,V[E[j,k+1]].x,V[E[j,k+1]].y,(X-Scene[win].M.Cx)/Scene[win].M.Mash,(Scene[win].M.Cy-Y)/Scene[win].M.Mash)
then FindRb(E[j,k],E[j,k+1]);
2: if
LinEx(win,V[E[j,k]].x,V[E[j,k]].z,V[E[j,k+1]].x,V[E[j,k+1]].z,(X-Scene[win].M.Cx)/Scene[win].M.Mash,(Scene[win].M.Cy-Y)/Scene[win].M.Mash)
then FindRb(E[j,k],E[j,k+1]);
3: if
LinEx(win,V[E[j,k]].y,V[E[j,k]].z,V[E[j,k+1]].y,V[E[j,k+1]].z,(X-Scene[win].M.Cx)/Scene[win].M.Mash,(Scene[win].M.Cy-Y)/Scene[win].M.Mash)
then FindRb(E[j,k],E[j,k+1]);
end;
end;
case win of
1: if
LinEx(win,V[E[j,E[j,0]]].x,V[E[j,E[j,0]]].y,V[E[j,1]].x,V[E[j,1]].y,(X-Scene[win].M.Cx)/Scene[win].M.Mash,(Scene[win].M.Cy-Y)/Scene[win].M.Mash)
then FindRb(E[j,E[j,0]],E[j,1]);
2: if
LinEx(win,V[E[j,E[j,0]]].x,V[E[j,E[j,0]]].z,V[E[j,1]].x,V[E[j,1]].z,(X-Scene[win].M.Cx)/Scene[win].M.Mash,(Scene[win].M.Cy-Y)/Scene[win].M.Mash)
then FindRb(E[j,E[j,0]],E[j,1]);
3: if LinEx(win,V[E[j,E[j,0]]].y,V[E[j,E[j,0]]].z,V[E[j,1]].y,V[E[j,1]].z,(X-Scene[win].M.Cx)/Scene[win].M.Mash,(Scene[win].M.Cy-Y)/Scene[win].M.Mash)
then FindRb(E[j,E[j,0]],E[j,1]);
end;
end;
SelReber:=rez;
end;
Procedure
PenRebPr(d,ind1,ind2:integer);
var t:integer;
begin
WindowProection[d].Canvas.Pen.Color:=clRed;
WindowProection[d].Canvas.MoveTo(Ser(d,V[ind1],Scene[d].M).X,Ser(d,V[ind1],Scene[d].M).Y);
WindowProection[d].Canvas.LineTo(Ser(d,V[ind2],Scene[d].M).X,Ser(d,V[ind2],Scene[d].M).Y);
end;
//* Нормальный вектор к
грани
Function TForm1.Normal
(A,B,C:Point):Vector;
begin
Normal.x:=((B.y-A.y)*(C.z-B.z))-((B.z-A.z)*(C.y-B.y));
Normal.y:=((B.z-A.z)*(C.x-B.x))-((B.x-A.x)*(C.z-B.z));
Normal.z:=((B.x-A.x)*(C.y-B.y))-((B.y-A.Y)*(C.x-B.x));
end;
//* Реализация поворота
Procedure
Rotate(Ax,Ay,Az:real;Ox,Oy,Oz:real);{поворот вокруг оси все точки
многогранника}
procedure Transfer(var
T:Point;Ox,Oy,Oz:real);
var W:Point;
begin
T.x:=T.x-Ox;
T.y:=T.y-Oy;
T.z:=T.z-Oz;
end;
Procedure UnTransfer(var
T:Point;Ox,Oy,Oz:real);
var W:Point;
begin
T.x:=T.x+Ox;
T.y:=T.y+Oy;
T.z:=T.z+Oz;
end;
Procedure RX(a:real; var
P:Point);{поворот вокруг оси OX одной точки}
var Q:Point;
begin Q.x:=P.x;
Q.y:=P.y*Cos(a)+P.z*Sin(a); Q.z:=-P.y*sin(a)+P.z*Cos(a); P:=Q end;
Procedure RY(a:real; var
P:Point);{поворот вокруг оси OY одной точки}
var Q:Point;
begin
Q.x:=P.x*Cos(a)-P.z*Sin(a);Q.y:=P.y;Q.z:=P.x*sin(a)+P.z*Cos(a); P:=Q end;
Procedure RZ(a:real; var
P:Point);{поворот вокруг оси OZ одной точки}
var Q:Point;
begin
Q.x:=P.x*Cos(a)-P.y*Sin(a);Q.y:=P.x*Sin(a)+P.y*Cos(a);Q.z:=P.z; P:=Q end;
var i:integer;
begin
if Form1.N17.Checked then
for i:=1 to Count do
begin
Transfer(InterPoint[i],Ox,Oy,Oz);RX(Ax,InterPoint[i]);RY(Ay,InterPoint[i]);RZ(Az,InterPoint[i]);UnTransfer(InterPoint[i],Ox,Oy,Oz)
end;
for i:=1 to N do begin
Transfer(V[i],Ox,Oy,Oz);RX(Ax,V[i]);RY(Ay,V[i]);RZ(Az,V[i]);UnTransfer(V[i],Ox,Oy,Oz);
end;
end;
//* Реализация
перемещение
Procedure
Move(Lx,Ly,Lz:real);
var i:integer;
begin
if Form1.N17.Checked then
for i:=1 to Count do
begin
InterPoint[i].x:=InterPoint[i].x+Lx;InterPoint[i].y:=InterPoint[i].y+Ly;InterPoint[i].z:=InterPoint[i].z+Lz;
end;
for i:=1 to N do begin
V[i].x:=V[i].x+Lx;V[i].y:=V[i].y+Ly;V[i].z:=V[i].z+Lz end;
end;
//* Размещение осей
перемещения
Procedure MoveOs;
begin
if
Form1.Centr.Left+Form1.Centr.Width>Form1.ClientWidth then
Form1.Centr.Left:=Form1.ClientWidth-Form1.Centr.Width;
if
Form1.Centr.Top+Form1.Centr.Height>Form1.GroupBox1.Top then
Form1.Centr.Top:=Form1.GroupBox1.Top-Form1.Centr.Height;
if
Form1.Centr.Top<Form1.ToolBar1.Top+Form1.ToolBar1.Height then
Form1.Centr.Top:=Form1.ToolBar1.Top+Form1.ToolBar1.Height;
Form1.Vertikal.Top:=Form1.ToolBar1.Height;
Form1.Vertikal.Left:=Form1.Centr.Left;
Form1.Vertikal.Height:=Form1.GroupBox1.Top-Form1.ToolBar1.Height;
Form1.Vertikal.Width:=Form1.Centr.Width;
Form1.Horizontal.Top:=Form1.Centr.Top;
Form1.Horizontal.Left:=0;
Form1.Horizontal.Height:=Form1.Centr.Height;
Form1.Horizontal.Width:=Form1.ClientWidth
end;
//* Размещение окон
проекций.
Procedure MoveWindow;
var i:byte;
begin
{Вид сверху}
Form1.PTop.Top:=Form1.ToolBar1.Height;
Form1.PTop.Left:=0;
Form1.PTop.Height:=Form1.Centr.Top-Form1.PTop.Top;
Form1.PTop.Width:=Form1.Centr.Left;
{Вид спереди}
Form1.PFront.Top:=Form1.ToolBar1.Height;
Form1.PFront.Left:=Form1.Centr.Left+Form1.Centr.Width;
Form1.PFront.Height:=Form1.Centr.Top-Form1.PFront.Top;
Form1.PFront.Width:=Form1.ClientWidth-Form1.Centr.Left-Form1.Centr.Width;
{Вид слева}
Form1.PLeft.Top:=Form1.Centr.Top+Form1.Centr.Height;
Form1.PLeft.Left:=0;
Form1.PLeft.Height:=Form1.GroupBox1.Top-Form1.PLeft.Top;
Form1.PLeft.Width:=Form1.Centr.Left;
{Окно перспективы}
Form1.PPerspective.Top:=Form1.Centr.Top+Form1.Centr.Height;
Form1.PPerspective.Left:=Form1.Centr.Left+Form1.Centr.Width;
Form1.PPerspective.Height:=Form1.GroupBox1.Top-Form1.PPerspective.Top;
Form1.PPerspective.Width:=Form1.ClientWidth-Form1.Centr.Left-Form1.Centr.Width;
{Задаем координаты
мирового центра}
for i:=1 to 4 do
begin
Scene[i].M.Cx:=WindowProection[i].Width
div 2;
Scene[i].M.Cy:=WindowProection[i].Height
div 2;
end;
end;
//* Вывод точек сечения
Procedure Puk;
var i,j:byte;
begin
for j:=1 to Count do
for i:=1 to 3 do
begin
WindowProection[i].Canvas.Pen.Color:=ColorPointIntersection;
WindowProection[i].Canvas.Ellipse(Ser(i,InterPoint[j],Scene[i].M).X-SizeT,Ser(i,InterPoint[j],Scene[i].M).Y-SizeT,Ser(i,InterPoint[j],Scene[i].M).X+SizeT,Ser(i,InterPoint[j],Scene[i].M).Y+SizeT);
end;
end;
//* Построение сечения
Procedure BildInter;
var i,j:integer;
Dipol:array[1..gran,1..2]of
Point;
Para,Count:integer;
Gp:array[0..gran]of
Point;
Procedure
UravPl(A1,A2,A3:Point; var A,B,C,D:real);{Уравнение плоскости сечения}
var P:Vector;
begin
p:=Form1.Normal(A1,A2,A3);
A:=p.x;
B:=p.y;
C:=P.z;
D:=-((A*A1.x)+(B*A1.y)+(C*A1.z))
end;
Function Sec(n,p:Point;
A,B,C,D:real; var IP:Point):boolean;{Точки сечения}
var
Kx,Ky,Kz,P1,P2,P3:real;
Yes:boolean;
begin
Yes:=false;
P1:=(A*n.x)+(B*n.y)+(C*n.z)+D;
P2:=(A*p.x)+(B*p.y)+(C*p.z)+D;
if P1=0 then begin IP:=n;
Yes:=true end
else if P2=0 then begin
IP:=p; Yes:=true end else
if P1*P2<0 then
begin
Yes:=true;
P1:=n.x-p.x; P2:=n.y-p.y;
P3:=n.z-p.z;
if P1=0 then IP.x:=n.x
else
begin
Kx:=((B*P2)+(C*P3))/P1;
IP.x:=((Kx*n.x)-(B*n.y)-(C*n.z)-D)/(A+Kx);
end;
if P2=0 then IP.y:=n.y
else
begin
Ky:=((A*P1)+(C*P3))/P2;
IP.y:=((Ky*n.y)-(A*n.x)-(C*n.z)-D)/(B+Ky);
end;
if P3=0 then IP.z:=n.z
else
begin
Kz:=((A*P1)+(B*P2))/P3;
IP.z:=((Kz*n.z)-(A*n.x)-(B*n.y)-D)/(C+Kz);
end;
end;
Sec:=Yes;
end;
Procedure Cep;{Построение
многоугольника сечения}
Function
RavPoi(a,b:point; Er:real):boolean;
var rez:boolean;
begin
rez:=false;
if abs(a.x-b.x)<Er
then
if abs(a.y-b.y)<Er
then
if abs(a.z-b.z)<Er
then rez:=true;
RavPoi:=rez;
end;
var i,j:integer;
h,f:Point;
begin
for i:=1 to Count-1 do
begin
for j:=i+1 to Count do
begin
if
RavPoi(Dipol[j,1],Dipol[i,2],Lok) then
begin
h:=Dipol[i+1,1];
f:=Dipol[i+1,2];
Dipol[i+1,1]:=Dipol[j,1];
Dipol[i+1,2]:=Dipol[j,2];
Dipol[j,1]:=h;
Dipol[j,2]:=f;
Break;
end;
if
RavPoi(Dipol[j,2],Dipol[i,2],Lok) then
begin
h:=Dipol[i+1,1];
f:=Dipol[i+1,2];
Dipol[i+1,1]:=Dipol[j,2];
Dipol[i+1,2]:=Dipol[j,1];
Dipol[j,2]:=h;
Dipol[j,1]:=f;
Break;
end;
end;
end;
Form1.Label1.Caption:='Сечение-
'+inttostr(Count)+' угольник.';
E[M+1,0]:=Count;
for i:=1 to Count do
begin
V[N+i]:=Dipol[i,1];
E[M+1,i]:=N+i;
end;
for i:=1 to 3 do
begin
Scene[i].G[M+1].Visible:=true;
Scene[i].G[M+1].Paint:=true;
Scene[i].G[M+1].BrushGr:=true;
end;
end;
begin
UravPl(InterPoint[1],InterPoint[2],InterPoint[3],A,B,C,D);
Count:=0;
for i:=1 to M do
begin
Para:=0;
for j:=1 to E[i,0]-1 do
begin
if
Sec(V[E[i,j]],V[E[i,j+1]],A,B,C,D,Gp[Para]) then inc(para);
if Para>2 then Break;
end;
if
Sec(V[E[i,E[i,0]]],V[E[i,1]],A,B,C,D,Gp[Para])then inc(para);
if Para=2 then
begin
inc(Count);
Dipol[Count,1]:=Gp[0];
Dipol[Count,2]:=Gp[1];
end;
end;
if Count>2 then
begin
Form1.IntWiew.Enabled:=true;
Cep;
end;
end;
Procedure
WindowsMove(X,Y,i:integer;shift:TShiftState);
var a,b,c:string;
h,k:integer;
Par:TPoint;
t,firsttrue:boolean;
begin
firsttrue:=false;
if MPI then begin
MoveP(i,kl,X,Y); MPI:=false end;
Form1.StatusBar2.Panels[0].Text:='X=
'+floattostrf(UnSer(i,X,Y,0,0,0,Scene[i].M).x,ffGeneral,3,5);
Form1.StatusBar2.Panels[1].Text:='Y=
'+floattostrf(UnSer(i,X,Y,0,0,0,Scene[i].M).y,ffGeneral,3,5);
Form1.StatusBar2.Panels[2].Text:='Z=
'+floattostrf(UnSer(i,X,Y,0,0,0,Scene[i].M).z,ffGeneral,3,5);
if (ssleft in shift) and
Form1.N34.Checked then
if Scene[i].M.Mash-(Y-Y0)>0
then Scene[i].M.Mash:=Scene[i].M.Mash-(Y-Y0) else ShowMessage('Масштаб: меньше
нельзя!');
if Form1.N8.Checked and
((i=1) or (i=2))then X0:=X;
if Form1.N9.Checked and
(i=1) then Y0:=Y;
if Form1.N10.Checked and
((i=2)or(i=3)) then Y0:=Y;
if Form1.N9.Checked and
(i=3) then X0:=X;
if Form1.N36.Checked then
begin
k:=SelectGran(i,X,Y);
if k<>0 then
begin
t:=Scene[i].G[k].Paint;
Scene[i].G[k].Paint:=false;
Form1.Repaint;
Scene[i].G[k].Paint:=t;
end
else Form1.Repaint;
end;
if Form1.N37.Checked then
begin
k:=SelectGran(i,X,Y);
if k<>0 then
begin
t:=Scene[i].G[k].Paint;
Scene[i].G[k].Paint:=true;
Form1.Repaint;
Scene[i].G[k].Paint:=t;
end
else Form1.Repaint;
end;
if Form1.N27.Checked and
Form1.IntWiew.Enabled then
for h:=1 to 3 do if
First[h] then
begin
Firsttrue:=true;
Form1.Repaint;
if SelReber(i,x,y,Par)
then
PenRebPr(i,Par.x,Par.y);
end;
if ssleft in shift then
begin
if Form1.N27.Checked and
Form1.IntWiew.Enabled and (not FirstTrue)then
begin
SelectPointIntersection(i,X,Y,kl);
if kl<>0 then
begin
MoveP(i,kl,X,Y);
MPI:=true
end
else MPI:=false
end;
if Form1.N29.Checked then
if Form1.N12.Checked then
Rotate((UnSer(i,Y,X,0,0,0,Scene[i].M).x-UnSer(i,Y0,X0,0,0,0,Scene[i].M).x)*Pi/180*Scene[i].M.Mash,(UnSer(i,Y,X,0,0,0,Scene[i].M).y-UnSer(i,Y0,X0,0,0,0,Scene[i].M).y)*Pi/180*Scene[i].M.Mash,(UnSer(i,Y,X,0,0,0,Scene[i].M).z-UnSer(i,Y0,X0,0,0,0,Scene[i].M).z)*Pi/180*Scene[i].M.Mash,V[1].x,V[1].y,V[1].z)
else if Form1.N13.Checked
then
Rotate((UnSer(i,Y,X,0,0,0,Scene[i].M).x-UnSer(i,Y0,X0,0,0,0,Scene[i].M).x)*Pi/180*Scene[i].M.Mash,(UnSer(i,Y,X,0,0,0,Scene[i].M).y-UnSer(i,Y0,X0,0,0,0,Scene[i].M).y)*Pi/180*Scene[i].M.Mash,(UnSer(i,Y,X,0,0,0,Scene[i].M).z-UnSer(i,Y0,X0,0,0,0,Scene[i].M).z)*Pi/180*Scene[i].M.Mash,0,0,0);
if Form1.N28.Checked then
Move(UnSer(i,X,Y,0,0,0,Scene[i].M).x-UnSer(i,X0,Y0,0,0,0,Scene[i].M).x,UnSer(i,X,Y,0,0,0,Scene[i].M).y-UnSer(i,X0,Y0,0,0,0,Scene[i].M).y,UnSer(i,X,Y,0,0,0,Scene[i].M).z-UnSer(i,X0,Y0,0,0,0,Scene[i].M).z);
X0:=X; Y0:=Y;
Form1.Repaint;
end;
end;
procedure
TForm1.N5Click(Sender: TObject);
begin
Form1.Close;
end;
//* Изминение размер окон
проекций
procedure
TForm1.CentrMouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
begin
if ssLeft in Shift then
begin
if
(Form1.Centr.Left+X>=0)and(Form1.Centr.Left+X<Form1.ClientWidth-Form1.Centr.Width)
then
Form1.Centr.Left:=Form1.Centr.Left+X;
if
(Form1.Centr.Top+Y>=Form1.ToolBar1.Height)and((Form1.Centr.Top+Y)<=(Form1.ToolBar1.Height+Form1.Vertikal.Height-Form1.Centr.Height))
then
Form1.Centr.Top:=Form1.Centr.Top+Y;
MoveOs;
end
end;
procedure
TForm1.CentrMouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
begin
MoveWindow;
end;
procedure
TForm1.FormCreate(Sender: TObject);
var i:byte;
begin
//* Присваиваем ярлыки
WindowProection[1]:=Form1.ITop;
WindowProection[2]:=Form1.IFront;
WindowProection[3]:=Form1.ILeft;
WindowProection[4]:=Form1.IPerspective;
PanelWindow[1]:=Form1.PTop;
PanelWindow[2]:=Form1.PFront;
PanelWindow[3]:=Form1.PLeft;
PanelWindow[4]:=Form1.PPerspective;
Magnit[1]:=Mag1;
Magnit[2]:=Mag2;
Magnit[3]:=Mag3;
//* Первоначальная
установка цвета
ActivColor:=clYellow;
ColorEder:=clAqua;
ColorUnEder:=clSilver;
ColorRebro:=clBlack;
ColorIntersection:=clRed;
ColorPointIntersection:=clBlue;
ColorNet:=clBtnFace;
//* Рапологаем окна
проекций и оси
MoveWindow;
MoveOs;
//* Задаем масштаб окон
проекций
for i:=1 to 3 do
Scene[i].M.Mash:=100;
Scene[4].M.Mash:=50;
for i:=1 to 3 do
First[i]:=false;
//Установка режима
Form1.IntWiew.Enabled:=false;
Count:=0;
MPI:=false;
//Активация вида сверху
ActivWindowProection(1);
end;
procedure
TForm1.FormResize(Sender: TObject);
begin
MoveOs;
MoveWindow;
end;
//Загрузка многогранника
из файла
procedure
TForm1.N2Click(Sender: TObject);
var
f:textfile;
i,j,k,l:integer;
Max,Q:real;
begin
if Form1.OD1.Execute then
begin
assignfile(f,Form1.OD1.FileName);
reset(f);
readln(f,N);
for i:=1 to N do{загрузка
координат вершин}
readln(f,V[i].x,V[i].y,V[i].z);
readln(f,M);
for i:=1 to M do
begin
j:=0;
while not eoln(f)
do{загрузка граней}
begin
inc(j);
read(f,E[i,j]);
end;
readln(f);
E[i,0]:=j;
end;
Form1.StatusBar2.Panels[3].Text:='Файл:
'+Form1.OD1.FileName;
Form1.N3.Enabled:=true;
Form1.ToolButton2.Enabled:=true;
closefile(f);
for i:=1 to 4 do
begin
for j:=1 to M
do{Установка вида изображения}
begin
Scene[i].G[j].Paint:=true;
Scene[i].G[j].BrushGr:=true;
Scene[i].G[j].PenRb:=false;
Scene[i].G[j].ColorRb:=ColorRebro;
Form1.N21.Checked:=false;
Form1.N22.Checked:=true;
Form1.N41.Click;
Num:=1;
end;
Max:=sqrt(sqr(V[1].x-V[N].x)+sqr(V[1].y-V[N].y)+sqr(V[1].z-V[N].z));
for l:=1 to N-1 do
for k:=1 to N-1 do
begin
Q:=sqrt(sqr(V[i].x-V[l].x)+sqr(V[i].y-V[l].y)+sqr(V[i].z-V[l].z));
if Q>Max then Max:=Q
end;
for k:=1 to 4 do
Scene[k].M.Mash:=WindowProection[k].Height/Max;
end;
Form1.Repaint;
end;
end;
procedure TForm1.ITopClick(Sender:
TObject);
begin
if not Scene[1].Active
then{Активация окна проекции вид сверху}
ActivWindowProection(1);
end;
procedure
TForm1.IFrontClick(Sender: TObject);
begin
if not Scene[2].Active
then{Активация окна проекции вид спереди}
ActivWindowProection(2);
end;
procedure
TForm1.ILeftClick(Sender: TObject);
begin
if not Scene[3].Active
then{Активация окна проекции вид слева}
ActivWindowProection(3);
end;
procedure
TForm1.ITopMouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
begin
if Scene[1].Active then
begin
WindowsMove(X,Y,1,shift);
end;
end;
procedure
TForm1.IFrontMouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
begin
if Scene[2].Active then
WindowsMove(X,Y,2,shift);
end;
procedure
TForm1.ILeftMouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
begin
if Scene[3].Active then
WindowsMove(X,Y,3,shift);
end;
//* Сохранение
многогранника
procedure
TForm1.N3Click(Sender: TObject);
var
f:textfile;
i,j:integer;
begin
if Form1.SD1.Execute then
begin
assignfile(f,Form1.SD1.FileName+'.txt');
rewrite(f);
writeln(f,N);
for i:=1 to N do{запись
координат вершин}
begin
writeln(f,V[i].x:5:3,'
',V[i].y:5:3,' ',V[i].z:5:3);
end;
writeln(f,M);
for i:=1 to M do
begin
for j:=1 to E[i,0]
do{запись обхода гнаней}
write(f,' ',E[i,j]);
writeln(f);
end;
Form1.StatusBar2.Panels[3].Text:='Файл:
'+Form1.SD1.FileName;
closefile(f);
Repaint;
end;
end;
procedure
TForm1.N33Click(Sender: TObject);
begin
ShowMessage('Курсовая
работа. Мосин Е.В. ФМ-43');
end;
procedure
TForm1.ToolButton1Click(Sender: TObject);
begin
Form1.N2.Click;
end;
procedure
TForm1.ToolButton2Click(Sender: TObject);
begin
Form1.N3.Click;
end;
//* Перерисовка формы
procedure
TForm1.FormPaint(Sender: TObject);
Procedure
ColorLight(i:integer;ColorEder,ColorUnEder:TColor);
var
j:integer;
n:vector;
c:real;
NorVec:array[1..4]of
real;
begin
{Нормальный вектор}
n:=Normal(V[E[i,1]],V[E[i,2]],V[E[i,3]]);
NorVec[1]:=n.z;NorVec[2]:=n.y;NorVec[3]:=n.x;NorVec[4]:=n.z;
for j:=1 to 4 do
Scene[j].G[i].Visible:=NorVec[j]>0;
{Освещенность}
c:=sqrt(sqr(n.x)+sqr(n.y)+sqr(n.z));
for j:=1 to 4 do
if Scene[j].G[i].Visible
then
Scene[j].G[i].colorgr:=(round(NorVec[j]/c*(ColorEder
mod 256))*$1)+(round(NorVec[j]/c*((ColorEder div $100) mod
256))*$100)+(round(NorVec[j]/c*((ColorEder div $10000) mod 256))*$10000)
else if c<>0 then
Scene[j].G[i].colorgr:=abs((round(NorVec[j]/c*(ColorUnEder
mod 256))*$1)+(round(NorVec[j]/c*((ColorUnEder div $100) mod
256))*$100)+(round(NorVec[j]/c*((ColorUnEder div $10000) mod 256))*$10000));
end;
var
i,j:integer;
k:TColor;
begin
{Стираем старое
изображение}
for j:=1 to 4 do
WindowProection[j].Picture:=nil;
for i:=1 to M do
ColorLight(i,ColorEder,ColorUnEder);
if Form1.IntWiew.Enabled
then
begin
BildInter;
ColorLight(M+1,ColorIntersection,ColorIntersection);
for j:=1 to 3 do
Scene[j].G[M+1].Visible:=true;
end;
DrawGrane;
Puk;
end;
//* Задание точек сечения
Procedure
EnterPointIntersection(i:byte;X,Y:integer);
var k:integer;
Par:TPoint;
begin
if Scene[i].Active then
begin
X0:=X;
Y0:=Y;
if Form1.N36.Checked then
begin
k:=SelectGran(i,X,Y);
if k<>0 then
Scene[i].G[k].Paint:=false;
end;
if Form1.N37.Checked then
begin
k:=SelectGran(i,X,Y);
if k<>0 then
Scene[i].G[k].Paint:=true;
end;
if Form1.N40.Checked then
begin
inc(Count);
InterPoint[Count]:=UnSer(i,X,Y,0,0,0,Scene[i].M);
Puk;
if Count=3 then
begin
Form1.N40.Checked:=false;
Form1.N40.Enabled:=false;
Form1.N41.Enabled:=true;
Form1.ToolButton13.Enabled:=false;
BildInter;
end;
end;
if Form1.N27.Checked and
Form1.IntWiew.Enabled then
for k:=1 to 3 do
if First[k] and
SelReber(i,x,y,Par) then
begin
MagPoint[k,1]:=V[Par.x];
MagPoint[k,2]:=V[Par.y];
First[k]:=false;
end;
Form1.Repaint;
end;
end;
procedure
TForm1.ITopMouseDown(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
begin
EnterPointIntersection(1,X,Y);
end;
procedure
TForm1.IFrontMouseDown(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
begin
EnterPointIntersection(2,X,Y);
end;
procedure
TForm1.ILeftMouseDown(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
begin
EnterPointIntersection(3,X,Y);
end;
//* Включение сетки
procedure
TForm1.N25Click(Sender: TObject);
var i:byte;
begin
for i:=1 to 3 do
if Scene[i].Active then
Scene[i].M.Net:=not
Scene[i].M.Net;
Form1.Repaint;
end;
//* Включение ребер
procedure
TForm1.N21Click(Sender: TObject);
var i,j:integer;
begin
Form1.N21.Checked:=not
Form1.N21.Checked;
for i:=1 to 4 do
for j:=1 to M do
Scene[i].G[j].PenRb:=Form1.N21.Checked;
Form1.Repaint;
end;
//* Включение заливки
procedure
TForm1.N22Click(Sender: TObject);
var i,j:integer;
begin
Form1.N22.Checked:=not
Form1.N22.Checked;
for i:=1 to 3 do
for j:=1 to M do
Scene[i].G[j].BrushGr:=Form1.N22.Checked;
Form1.Repaint;
end;
//* Вызов диалога
изменения цвета
procedure
TForm1.N16Click(Sender: TObject);
begin
Application.CreateForm(TForm2,Form2);
end;
//* Вызов окна просмотра
сечения
procedure
TForm1.IntWiewClick(Sender: TObject);
begin
Application.CreateForm(TForm3,Form3);
end;
//Панель
инструментов--------------------------------------
procedure TForm1.N8Click(Sender:
TObject);
var i:integer;
begin
Form1.ToolButton12.Down:=Form1.N8.Checked;
end;
procedure
TForm1.N27Click(Sender: TObject);
begin
Form1.ToolButton4.Down:=true;
end;
procedure
TForm1.N28Click(Sender: TObject);
begin
Form1.ToolButton5.Down:=true;
end;
procedure
TForm1.N29Click(Sender: TObject);
begin
Form1.ToolButton6.Down:=true;
end;
procedure
TForm1.N34Click(Sender: TObject);
begin
Form1.ToolButton7.Down:=true;
end;
procedure
TForm1.N36Click(Sender: TObject);
begin
Form1.ToolButton8.Down:=true;
end;
procedure
TForm1.N37Click(Sender: TObject);
begin
Form1.ToolButton9.Down:=true;
end;
procedure
TForm1.N9Click(Sender: TObject);
begin
Form1.ToolButton11.Down:=Form1.N9.Checked;
end;
procedure
TForm1.N10Click(Sender: TObject);
begin
Form1.ToolButton19.Down:=Form1.N10.Checked;
end;
//---------------------------------------------------------
procedure
TForm1.IPerspectiveClick(Sender: TObject);
begin
if not Scene[4].Active
then{Активация окна перспективы}
ActivWindowProection(4);
end;
//* Удаление сечения
procedure
TForm1.N41Click(Sender: TObject);
var i:integer;
begin
Count:=0;
for i:=1 to 3 do
First[i]:=false;
Form1.N40.Enabled:=true;
Form1.N40.Checked:=false;
Form1.N41.Enabled:=false;
Form1.ToolButton13.Enabled:=true;
Form1.ToolButton13.Down:=false;
Form1.IntWiew.Enabled:=false;
Form1.Label1.Caption:='Сечение
не задано.';
for i:=1 to 3 do
Scene[i].G[M+1].Visible:=false;
Form1.Repaint;
end;
//* Сброс
procedure
TForm1.N14Click(Sender: TObject);
var i:integer;
begin
ActivColor:=clYellow;
ColorEder:=clAqua;
ColorUnEder:=clSilver;
ColorRebro:=clBlack;
ColorIntersection:=clRed;
ColorPointIntersection:=clBlue;
ColorNet:=clBtnFace;
for i:=1 to 3 do
Scene[i].M.Mash:=100;
Form1.N41.Click;
M:=0;
N:=0;
Form1.StatusBar2.Panels[3].Text:='Файл
не загружен';
Form1.Repaint;
end;
//---------------------------------------------------------
procedure
TForm1.N18Click(Sender: TObject);
begin
Form1.Repaint;
end;
procedure
TForm1.ToolButton4Click(Sender: TObject);
begin
Form1.N27.Click;
end;
procedure
TForm1.ToolButton5Click(Sender: TObject);
begin
Form1.N28.Click;
end;
procedure
TForm1.ToolButton6Click(Sender: TObject);
begin
Form1.N29.Click;
end;
procedure
TForm1.ToolButton7Click(Sender: TObject);
begin
Form1.N34.Click;
end;
procedure
TForm1.ToolButton8Click(Sender: TObject);
begin
Form1.N36.Click;
end;
procedure
TForm1.ToolButton9Click(Sender: TObject);
begin
Form1.N37.Click;
end;
procedure
TForm1.ToolButton12Click(Sender: TObject);
begin
Form1.N8.Click;
end;
procedure
TForm1.ToolButton11Click(Sender: TObject);
begin
Form1.N9.Click;
end;
procedure
TForm1.ToolButton19Click(Sender: TObject);
begin
Form1.N10.Click;
end;
procedure
TForm1.ToolButton13Click(Sender: TObject);
begin
Form1.N40.Click;
end;
procedure TForm1.N24Click(Sender:
TObject);
begin
Form1.Repaint;
end;
procedure
TForm1.N19Click(Sender: TObject);
begin
Form1.Repaint;
end;
//---------------------------------------------------------
procedure
TForm1.Mag1Click(Sender: TObject);
begin
if Mag1.Checked then
First[1]:=true;
end;
procedure
TForm1.Mag2Click(Sender: TObject);
begin
if Mag2.Checked then
First[2]:=true;
end;
procedure
TForm1.Mag3Click(Sender: TObject);
begin
if Mag3.Checked then
First[3]:=true;
end;
end.
unit Unit2;
interface
uses
Windows, Messages,
SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls,
Buttons, ComCtrls, ExtCtrls;
type
TForm2 = class(TForm)
BitBtn1: TBitBtn;
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
Label4: TLabel;
Label5: TLabel;
Shape1: TShape;
Shape2: TShape;
Shape3: TShape;
Shape4: TShape;
Shape5: TShape;
Label6: TLabel;
Shape6: TShape;
CD1: TColorDialog;
Label7: TLabel;
Shape7: TShape;
procedure
FormCreate(Sender: TObject);
procedure
Shape1MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
procedure
Shape2MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
procedure
Shape3MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
procedure Shape4MouseUp(Sender:
TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
procedure
Shape5MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
procedure
Shape6MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
procedure
BitBtn1Click(Sender: TObject);
procedure
CD1Close(Sender: TObject);
procedure
Shape7MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form2: TForm2;
implementation
uses Unit1,Unit3;
{$R *.dfm}
procedure
TForm2.FormCreate(Sender: TObject);
begin
Shape1.Brush.Color:=ColorIntersection;
Shape2.Brush.Color:=ColorEder;
Shape3.Brush.Color:=ColorRebro;
Shape4.Brush.Color:=ColorNet;
Shape5.Brush.Color:=ActivColor;
Shape6.Brush.Color:=ColorPointIntersection;
Shape7.Brush.Color:=ColorUnEder;
end;
procedure
TForm2.Shape1MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
begin
if Form2.CD1.Execute then
begin
ColorIntersection:=Form2.CD1.Color;
Form2.Shape1.Brush.Color:=Form2.CD1.Color
end
end;
procedure
TForm2.Shape2MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
begin
if Form2.CD1.Execute then
begin
ColorEder:=Form2.CD1.Color;
Form2.Shape2.Brush.Color:=Form2.CD1.Color
end
end;
procedure
TForm2.Shape3MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
var i,j:word;
begin
if Form2.CD1.Execute then
begin
ColorRebro:=Form2.CD1.Color;
Form2.Shape3.Brush.Color:=Form2.CD1.Color;
for i:=1 to 3 do
for j:=1 to M do
Scene[i].G[j].ColorRb:=ColorRebro;
end
end;
procedure
TForm2.Shape4MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
begin
if Form2.CD1.Execute then
begin
ColorNet:=Form2.CD1.Color;
Form2.Shape4.Brush.Color:=Form2.CD1.Color
end
end;
procedure
TForm2.Shape5MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
begin
if Form2.CD1.Execute then
begin
ActivColor:=Form2.CD1.Color;
Form2.Shape5.Brush.Color:=Form2.CD1.Color
end
end;
procedure
TForm2.Shape6MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
begin
if Form2.CD1.Execute then
begin
ColorPointIntersection:=Form2.CD1.Color;
Form2.Shape6.Brush.Color:=Form2.CD1.Color
end
end;
procedure
TForm2.BitBtn1Click(Sender: TObject);
begin
Form2.Close
end;
procedure
TForm2.CD1Close(Sender: TObject);
begin
Form1.Repaint;
end;
procedure
TForm2.Shape7MouseUp(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y:
Integer);
begin
if Form2.CD1.Execute then
begin
ColorUnEder:=Form2.CD1.Color;
Form2.Shape7.Brush.Color:=Form2.CD1.Color
end
end;
end.
unit Unit3;
interface
uses
Windows, Messages,
SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls,
Buttons, ExtCtrls,Math;
type
TForm3 = class(TForm)
GroupBox1: TGroupBox;
ListBox1: TListBox;
Label1: TLabel;
Edit1: TEdit;
Label2: TLabel;
Edit2: TEdit;
Label3: TLabel;
Splitter1: TSplitter;
BitBtn1: TBitBtn;
procedure
FormCreate(Sender: TObject);
procedure
Edit2KeyPress(Sender: TObject; var Key: Char);
procedure
Edit1KeyPress(Sender: TObject; var Key: Char);
procedure
FormPaint(Sender: TObject);
procedure
FormMouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
procedure
BitBtn1Click(Sender: TObject);
private
{ Private declarations }
procedure
PaintIntersection;
public
{ Public declarations }
end;
var
Form3: TForm3;
CxW,CyW,X0W,Y0W:integer;
MashW:real;
PInter:array of TPoint;
implementation
uses Unit1,Unit2;
procedure
TForm3.PaintIntersection;
var i:integer;
Nor:Vector;
C1,S1,x:real;
FG:array[1..1000] of
Point;
begin
CxW:=(Form3.Width+Form3.GroupBox1.Width)
div 2;
CyW:=(Form3.Height) div
2;
for i:=1 to E[M+1,0] do
FG[i]:=V[N+i];
Nor:=Form1.Normal(FG[1],FG[2],FG[3]);
if (Nor.y<>0) and
(Nor.z<>0) then
begin
C1:=Nor.z/sqrt(sqr(Nor.y)+sqr(Nor.z));
S1:=Nor.y/sqrt(sqr(Nor.y)+sqr(Nor.z));
end
else begin C1:=1; S1:=0
end;
for i:=1 to E[M+1,0] do
begin
x:=(FG[i].y*C1)-(FG[i].z*S1);
FG[i].z:=(FG[i].y*S1)+(FG[i].z*C1);
FG[i].y:=x;
end;
Nor:=Form1.Normal(FG[1],FG[2],FG[3]);
if (Nor.x<>0) and
(Nor.z<>0) then
begin
C1:=Nor.z/sqrt(sqr(Nor.x)+sqr(Nor.z));
S1:=Nor.x/sqrt(sqr(Nor.x)+sqr(Nor.z));
end
else begin C1:=1; S1:=0
end;
for i:=1 to E[M+1,0] do
begin
FG[i].x:=(FG[i].x*C1)-(FG[i].z*S1);
end;
SetLength(PInter,E[M+1,0]);
for i:=1 to E[M+1,0] do
begin
PInter[i-1].X:=round(CxW+(FG[i].x*MashW));
PInter[i-1].Y:=round(CyW-(FG[i].y*MashW));
end;
Form3.Canvas.Brush.Color:=ColorIntersection;
Form3.Canvas.Pen.Color:=ColorRebro;
Form3.Canvas.Polygon(PInter);
Form3.Canvas.Font.Height:=8;
Form3.Canvas.Brush.Style:=bsClear;
Form3.Canvas.Pen.Color:=clBlack;
for i:=1 to E[M+1,0] do
Form3.Canvas.TextOut(PInter[i-1].X,PInter[i-1].Y,'S'+inttostr(i));
end;
{$R *.dfm}
procedure
TForm3.FormCreate(Sender: TObject);
function
Ploshad(A,B,C:Point):real;
var i:integer;
Al,Bl,Cl,p:real;
begin
Al:=sqrt(sqr(A.x-B.x)+sqr(A.y-B.y)+sqr(A.z-B.z));
Bl:=sqrt(sqr(B.x-c.x)+sqr(B.y-C.y)+sqr(B.z-C.z));
Cl:=sqrt(sqr(C.x-A.x)+sqr(C.y-A.y)+sqr(C.z-A.z));
p:=(Al+Bl+Cl)/2;
Ploshad:=sqrt(p*(p-Al)*(p-Bl)*(p-Cl));
end;
var i:integer;
S:real;
begin
Form3.Caption:='Просмотр
сечения. ('+inttostr(E[M+1,0])+' угольник)';
for i:=1 to E[M+1,0] do
Form3.ListBox1.Items[i-1]:='S'+inttostr(i)+':
'+floattostrf(V[E[M+1,i]].x,ffGeneral,3,5)+'; '+floattostrf(V[E[M+1,i]].y,ffGeneral,3,5)+';
'+floattostrf(V[E[M+1,i]].z,ffGeneral,3,5);
Form3.Edit2.Text:='('+floattostrf(A,ffGeneral,3,5)+')*X+('+floattostrf(B,ffGeneral,3,5)+')*Y+('+floattostrf(C,ffGeneral,3,5)+')*Z+('+floattostrf(D,ffGeneral,3,5)+')'+'=0';
CxW:=(Form3.Width+Form3.GroupBox1.Width)
div 2;
CyW:=(Form3.Height) div
2;
MashW:=Scene[4].M.Mash;
S:=0;
for i:=1 to E[M+1,0]-2 do
S:=S+Ploshad(V[M+1],V[M+i+1],V[M+i+2]);
Form3.Edit1.Text:=floattostrf(S,ffGeneral,3,5)+'
Ед.Кв.';
end;
procedure
TForm3.Edit2KeyPress(Sender: TObject; var Key: Char);
begin
Key:=#0;
end;
procedure
TForm3.Edit1KeyPress(Sender: TObject; var Key: Char);
begin
Key:=#0;
end;
procedure
TForm3.FormPaint(Sender: TObject);
begin
PaintIntersection;
end;
procedure
TForm3.FormMouseMove(Sender: TObject; Shift: TShiftState; X,
Y: Integer);
begin
if ssleft in shift then
begin
if MashW-(Y-Y0W)>0
then MashW:=MashW-(Y-Y0W) else ShowMessage('Масштаб: меньше нельзя!');
Form3.Repaint;
end;
X0W:=X; Y0W:=Y;
end;
procedure
TForm3.BitBtn1Click(Sender: TObject);
begin
Form3.Close;
end;
end.
Список
литературы
1.
Delphi
6. Справочное пособие. Архангельский А.Я. – М.: ЗАО «Издательство БИНОМ», 2001.
2.
Эффективная
работа: 3ds max 4. Маров М. – СПб.: Питер, 2002.
3.
Геометрия.
В 2-х ч. Ч. I. Учебное пособие для студентов физ.-мат. фак. пед. ин-тов.
Атанасян Л.С., Базылев В.Т. – М.: Просвещение, 1986.
|