Контрольная работа: Расчет вероятностей событий
Контрольная работа: Расчет вероятностей событий
Задание №1
Какова вероятность того, что наудачу взятое натуральное число не делится:
а) ни на два, ни на три;
б) на два или на три?
Решение:
Пусть А – событие, что натуральное число делится на 2→
p(A)=1/2 (каждое второе натуральное число кратно 2)
В-событие, что натуральное число делится на 3
p(В)=1/3 (каждое третье натуральное число кратно 3)
а) С – событие, что наудачу взятое натуральное число не делится ни на
два, ни на три 
Вероятность
произведения двух независимых событий А и В равна произведению их вероятностей
Тогда вероятность события С:
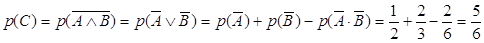
Т.е. пять из шести натуральных чисел не делится ни на 2 ни на 3
б) D – событие, что наудачу взятое натуральное число не делится на 2
или на 3 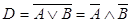 . .
Вероятность
суммы двух несовместных событий А и В равна сумме вероятностей этих событий
Тогда вероятность события D:
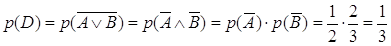 . .
Т.е. одно из трех натуральных чисел не делится на 2 или на 3
Задание №2
В ружейной пирамиде имеются винтовки двух систем: одна винтовка
типа 1 и две винтовки типа 2. Вероятность попасть в мишень при выстреле из
винтовки типа 1 равна р1, из винтовки типа 2 – р2.
Стрелок производит 7 выстрелов из наудачу взятой винтовки. Чему
равна вероятность того, что мишень окажется поражённой не менее пяти раз?
Решение:
А – событие, что поражена мишень
Пусть событие Н1 – винтовка I типа; событие Н2 – винтовка II типа.
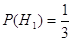 и и 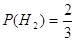
А/Н1 – мишень поражена при выстреле из винтовки I типа
А/Н2 – мишень поражена при выстреле из винтовки II типа
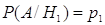
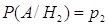
Для
нахождения вероятности 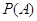 применяют формулу применяют формулу
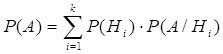
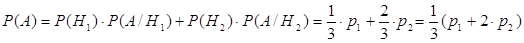
2. Рn (k) – вероятность, что в n испытаниях событие
наступит k раз находится по формуле Бернулли 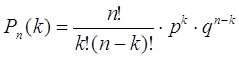 . .
Вероятность события, что мишень окажется
поражённой не менее пяти раз, если произведено 7 выстрелов из наудачу взятой
винтовки.
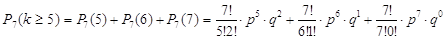
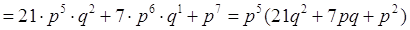
При измерении урожайности картофеля вес клубней в одном кусте распределился
по интервалам следующим образом:
| Х(кг) |
2,5–2,7 |
2,7–2,9 |
2,9–3,1 |
3,1–3,3 |
3,3–3,5 |
3,5–3,7 |
3,7–4,3 |
| К-во кустов |
50 |
150 |
200 |
250 |
150 |
100 |
100 |
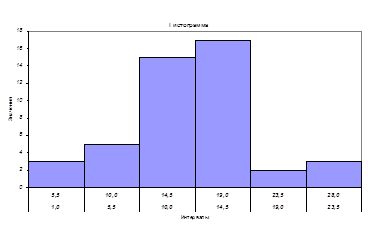
Построить гистограмму и найти средний вес одного куста.
Решение:
Гистограмма –
служит для изображения интервальных рядов и представляет собой ступенчатую
фигуру из прямоугольников с основаниями, равными интервалам значений признака 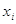 , и высотами, равными
частотам , и высотами, равными
частотам 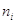 интервалов. интервалов.

Для расчета среднего веса одного куста воспользуемся формулой средней
арифметической.
Средней арифметической дискретного вариационного ряда 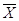 называется отношение суммы
произведений вариантов на соответствующие частоты к объему совокупности: называется отношение суммы
произведений вариантов на соответствующие частоты к объему совокупности:
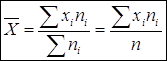
где 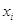 - варианты дискретного ряда
или середины интервалов вариационного ряда, - варианты дискретного ряда
или середины интервалов вариационного ряда, 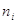 -
соответствующие им частоты. -
соответствующие им частоты.
Для каждого
интервала найдем середины по формуле 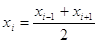 . .
| Х(кг) |
2,5–2,7 |
2,7–2,9 |
2,9–3,1 |
3,1–3,3 |
3,3–3,5 |
3,5–3,7 |
3,7–4,3 |
|
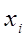
|
2,6 |
2,8 |
3 |
3,2 |
3,4 |
3,6 |
4 |
| К-во кустов |
50 |
150 |
200 |
250 |
150 |
100 |
100 |
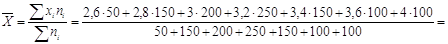
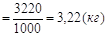
Ответ: средний вес одного куста составляет 3,22 кг.
Задание №4
По следующим данным построить интервальный вариационный ряд и гистограмму:
24, 14, 15, 26, 16, 17, 14, 15, 1, 11, 14, 12, 16, 17, 13, 10, 11, 12, 13, 15,
14, 10, 11, 14, 7, 15, 14, 15, 15, 14, 15, 14, 2, 5, 18, 19, 16, 17, 9, 10, 18,
19, 20, 22, 28.
Найти среднее значение, дисперсию и стандартное отклонение.
Решение:
1. Проранжируем[1] исходный ряд,
подсчитаем частоту вариантов. Получим вариационный ряд
2. Для
определения числа групп воспользуемся формулой Стерджесса:
n = 1+3,322 * lgN
где n – число групп, N =45 – число единиц
совокупности
Для данных
задачи n = 1 + 3,322*lg 45 = 1 + 3,322 * 1,65 =
6б49 »
6 групп
Величина интервала
представляет собой разность между максимальным и минимальным значением признака
в каждой группе.
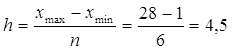
3. Выполним
промежуточные вычисления во вспомогательной таблице и определим значения
числовых характеристик:
Середины
интервалов 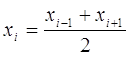
Средняя
арифметическая 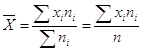 где где 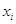 -
варианты дискретного ряда или середины интервалов вариационного ряда, -
варианты дискретного ряда или середины интервалов вариационного ряда, 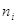 - соответствующие им частоты. - соответствующие им частоты.
Дисперсия 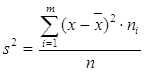 . .
Среднее
квадратическое отклонение 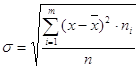 . .
| № |
Значения
|
|
|
№
группы |
Интервалы |
Частота |
| 1 |
1
|
|
|
нач
|
кон
|
| 2 |
2
|
|
|
1 |
1,0 |
5,5 |
3
|
| 3 |
5
|
|
|
2 |
5,5 |
10,0 |
5
|
| 4 |
7
|
|
|
3 |
10,0 |
14,5 |
15
|
| 5 |
9
|
|
|
4 |
14,5 |
19,0 |
17
|
| 6 |
10
|
|
|
5 |
19,0 |
23,5 |
2
|
| 7 |
10
|
|
|
6 |
23,5 |
28,0 |
3
|
| 8 |
10
|
|
|
|
|
|
|
| 9 |
11
|
|
|
|
|
|
|
| 10 |
11
|
|
|
|
|
|
|
| 11 |
11
|
|
|
|
|
|
|
| 12 |
12
|
|
|
|
|
|
|
| 13 |
12
|
|
|
|
|
|
|
| 14 |
13
|
|
|
|
|
|
|
| 15 |
13
|
|
|
|
|
|
|
| 16 |
14
|
|
|
|
|
|
|
| 17 |
14
|
|
|
|
|
|
|
| 18 |
14
|
|
|
|
|
|
|
| 19 |
14
|
|
|
|
|
|
|
| 20 |
14
|
|
|
|
|
|
|
| 21 |
14
|
|
|
|
|
|
|
| 22 |
14
|
|
|
|
|
|
|
| 23 |
14
|
|
|
|
|
|
|
| 24 |
15
|
|
|
|
|
|
|
| 25 |
15
|
|
|
|
|
|
|
| 26 |
15
|
|
|
|
|
|
|
| 27 |
15
|
|
|
|
|
|
|
| 28 |
15
|
|
|
|
|
|
|
| 29 |
15
|
|
|
|
|
|
|
| 30 |
15
|
|
|
|
|
|
|
| 31 |
16
|
|
|
|
|
|
|
| 32 |
16
|
|
|
|
|
|
|
| 33 |
16
|
|
|
|
|
|
|
| 34 |
17
|
|
|
|
|
|
|
| 35 |
17
|
|
|
|
|
|
|
| 36 |
17
|
|
|
|
|
|
|
| 37 |
18
|
|
|
|
|
|
|
| 38 |
18
|
|
|
|
|
|
|
| 39 |
19
|
|
|
|
|
|
|
| 40 |
19
|
|
|
|
|
|
|
| 41 |
20
|
|
|
|
|
|
|
| 42 |
22
|
|
x min
|
1
|
|
|
| 43 |
24
|
|
x max
|
28
|
|
|
| 44 |
26
|
|
h
|
4,5
|
|
|
| 45 |
28
|
|
|
|
|
|
|
| №
группы |
Интервалы |
Частота |
Промежуточные вычисления
|
|
нач
|
кон
|
сер
|
ni
|
xcp*ni
|
(x-Xcp)
|
(x-Xcp)2
|
ni*(x-Xcp)2
|
| 1 |
1,0 |
5,5 |
3,25 |
3
|
9,75 |
-10,9 |
118,81 |
356,43 |
| 2 |
5,5 |
10,0 |
7,75 |
5
|
38,75 |
-6,4 |
40,96 |
204,80 |
| 3 |
10,0 |
14,5 |
12,25 |
15
|
183,75 |
-1,9 |
3,61 |
54,15 |
| 4 |
14,5 |
19,0 |
16,75 |
17
|
284,75 |
2,6 |
6,76 |
114,92 |
| 5 |
19,0 |
23,5 |
21,25 |
2
|
42,50 |
7,1 |
50,41 |
100,82 |
| 6 |
23,5 |
28,0 |
25,75 |
3
|
77,25 |
11,6 |
134,56 |
403,68 |
|
|
|
|
|
45 |
636,75 |
|
|
1234,80
|
|
|
|
|
|
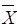
|
14,15 |
|
S2
|
27,44
|
|
|
|
|
|
|
|
|
5,24
|
Среднее
значение 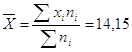
Дисперсия 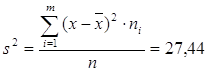
Среднее
квадратическое отклонение 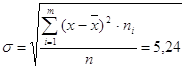
Ответ: 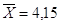 , , 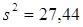 , , 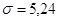
Задание №5
Некоторая случайная величина подчиняется закону нормального распределения
с математическим ожиданием 50 и дисперсией 36. Найти вероятность того, что
отдельное значение случайной величины заключено в интервале от 40 до 60.
Решение:
Пусть X – случайная величина подчиняется закону нормального распределения
По условию 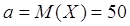 и и 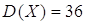
Найти: 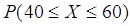
Для нормального распределения СВ X
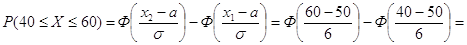
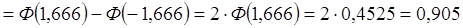
где Ф(Х) – функция Лапласа, дифференциальная функция нормального
закона имеет вид 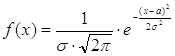 . .
Значения Ф(Х) – табулированы
Ответ: 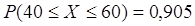
Задание №6
Определить вероятность того, что истинное значение расстояния отличается
от среднего (1000 м), полученного в 100 опытах, не более, чем на 5 м,
если стандартное отклонение 25 м.
Решение:
Пусть X – случайная величина расстояния, м
По условию 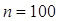 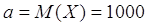 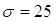 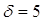
Найти: 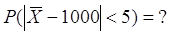
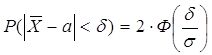
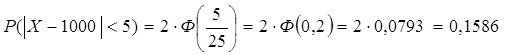
Ответ: 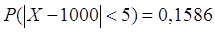
Задание №7
При измерении дальности расстояния дальномеры дали различные показания
так, что среднее расстояние оказалось 1000 м с выборочной дисперсией 36 м2.
В каких пределах находится истинное расстояние с вероятностью 80%, если
произведено 11 измерений.
Решение:
По условию задана выборка объемом 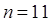 и дисперсия нормально
распределенной СВ X 36. Найдено выборочное среднее и дисперсия нормально
распределенной СВ X 36. Найдено выборочное среднее 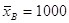 .
Требуется найти доверительный интервал для неизвестного математического
ожидания .
Требуется найти доверительный интервал для неизвестного математического
ожидания 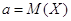 , если доверительная вероятность
должна быть равна , если доверительная вероятность
должна быть равна 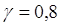
1. Доверительный интервал имеет общий вид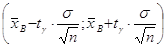
2. По условию 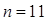 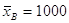 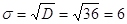 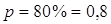
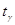 находим из решения
уравнения находим из решения
уравнения
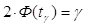 → → 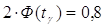 → → 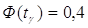
используя таблицу значений функции Лапласа 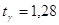
3. Находим значения концов доверительного
интервала
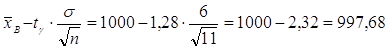 . .
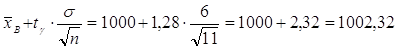 . .
Т.о., искомый доверительный интервал 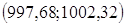 , т.е. , т.е. 
Ответ: 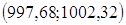
Задание №8
При
определении массы пяти таблеток лекарственного вещества получены следующие
результаты: 0,148; 0,149; 0,151; 0,153; 0,155 (г). Найти ошибку в определении
массы таблетки с вероятностью 80%.
Решение:
| xi |
1 |
2 |
3 |
4 |
5 |
| mi |
0,148 |
0,149 |
0,151 |
0,153 |
0,155 |
Вычислим
ошибку в определении массы таблетки с вероятностью 80% по формуле: 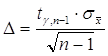 - предельная ошибка малой
выборки. - предельная ошибка малой
выборки.
Учитывая, что 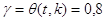 определим определим
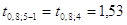 табулированные значения табулированные значения 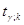 - критерия Стьюдента. - критерия Стьюдента.
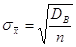
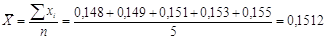
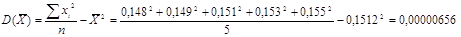
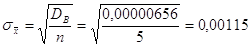 . .
Таким
образом,
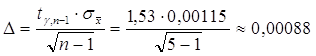 . .
Ответ: Ошибка в определении
массы таблетки с вероятностью 80% составляет 0,00088
При изменении
скорости реакции 2-х человек провели по сто опытов и получили следующие данные:
Xср = 100 мс, дисперсия
средних равна 9 мс2, Yср = 110 мс, дисперсия средних равна 16 мс2.
Проверить
гипотезу о равенстве математических ожиданий двух нормальных распределений для
уровня значимости 0,02.
Решение:
Пусть 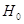 - гипотеза, математические
ожидания двух нормальных распределений для случайных величин X и Y равны. - гипотеза, математические
ожидания двух нормальных распределений для случайных величин X и Y равны.
При
достаточно больших объемах выборки выборочные средние 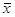 и и 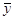 имеют приближенно
нормальный закон распределения с математическим ожиданием имеют приближенно
нормальный закон распределения с математическим ожиданием 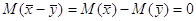 и дисперсией и дисперсией 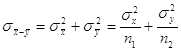 . .
При
выполнении гипотезы 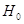 статистика статистика
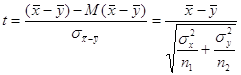 имеет стандартное нормальное распределение
N (0; 1) имеет стандартное нормальное распределение
N (0; 1)
По данным
задачи
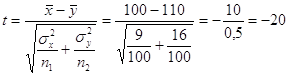
В случае
конкурирующей гипотезы 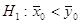 выбирают
одностороннюю критическую область, и критическое значение статистики находят из
условия выбирают
одностороннюю критическую область, и критическое значение статистики находят из
условия 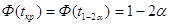
Т.о. 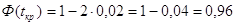
Табулированное
значение 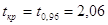
Если
фактические наблюдаемое значение статистики t больше критического tкр,
определенного на уровне значимости a (по абсолютной величине),
т.е. 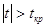 , то гипотеза , то гипотеза 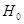 отвергается, в противном
случае – гипотеза отвергается, в противном
случае – гипотеза 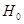 не противоречит
имеющимся наблюдениям. не противоречит
имеющимся наблюдениям.
Т.к.
наблюдаемое значение статистики 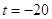 , а
критическое значение , а
критическое значение 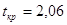 , то в силу
условия , то в силу
условия 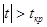 → →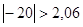 делаем ввод, что гипотеза делаем ввод, что гипотеза 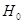 отвергается, т.е.
математические ожидания двух нормальных распределений для случайных величин X и
Y не равны. отвергается, т.е.
математические ожидания двух нормальных распределений для случайных величин X и
Y не равны.
Задание №10
Оцените
достоверность различия продолжительности жизни мужчин (X) и женщин (Y) для уровня значимости
0,10:
X
|
60 |
65 |
66 |
70 |
64 |
| Y |
72 |
71 |
80 |
78 |
69 |
Решение:
Пусть 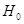 - гипотеза, достоверность
различия в продолжительности жизни мужчин и женщин на уровне значимости 0,10 - гипотеза, достоверность
различия в продолжительности жизни мужчин и женщин на уровне значимости 0,10
Вычислим 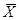 и и 
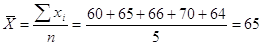
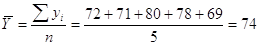
При
выполнении гипотезы 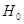 статистика статистика 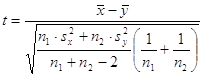 . .
где 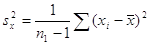 и и 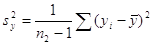
|
X
|
60 |
65 |
66 |
70 |
64 |
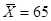
|
|
Y
|
72 |
71 |
80 |
78 |
69 |
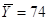
|
|
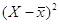
|
25 |
0 |
1 |
25 |
1 |
52
|
|
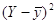
|
4 |
9 |
36 |
16 |
25 |
90
|
|
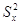
|
13
|
|
|
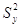
|
22,5
|
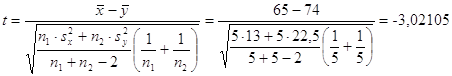
Критическое
значение статистики находят из условия 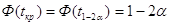 . .
Т.о. 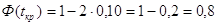 . .
Табулированное
значение 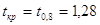 . .
Т.к.
наблюдаемое значение статистики  , а
критическое значение , а
критическое значение 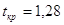 то в силу
условия то в силу
условия 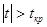 делаем ввод, что гипотеза делаем ввод, что гипотеза 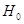 отвергается, т.е. достоверность
различия продолжительности жизни мужчин (X) и женщин (Y) для уровня значимости
0,10 не подтверждается. отвергается, т.е. достоверность
различия продолжительности жизни мужчин (X) и женщин (Y) для уровня значимости
0,10 не подтверждается.
По данным
наблюдений за последние 5 лет составили таблицу урожайности пшеницы и числа
дождливых дней за вегетативный период:
| Ц/ га |
10 |
15 |
6 |
20 |
9 |
| Число дождливых дней |
14 |
20 |
6 |
20 |
10 |
Коррелируют
ли данные величины?
Решение:
Для оценки тесноты корреляционной зависимости
между величинами Y и X используется коэффициент корреляции – показатель тесноты
линейной связи.
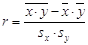
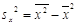 ( (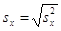 ) )
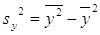 ( (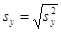 ) )
Свойства коэффициента корреляции:
1 0 Коэффициент корреляции удовлетворяет неравенству  . .
2 0 В зависимости от близости r к единице различают
связь слабую, умеренную, заметную, достаточно тесную, тесную и весьма тесную
Оценка тесноты линейной связи (шкала Чаддока)
|
Значение ½r½
|
0–0,1
|
0,1–0,3
|
0,3–0,5
|
0,5–0,7
|
0,7–0,9
|
0,9–0,99
|
1
|
|
Теснота
линейной
связи
|
Нет
связи
|
Слабая |
Умеренная |
Заметная |
Высокая |
Очень высокая |
Функциональная |
|
Значение R
|
Связь
|
Интерпретация связи
|
| R = 0 |
Отсутствует |
Отсутствует линейная связь между х и у |
| 0<R < 1 |
Прямая |
С увеличением х величина у в среднем
увеличивается и наоборот |
| -1<R<0 |
Обратная |
С увеличением х величина у в среднем
уменьшается и наоборот |
| R =+1 R = -1 |
Функциональная |
Каждому значению х соответствует одно
строго определенное значение величины у и наоборот |
|
|
Ц/га |
Число
дождливых дней |
Промежуточные
вычисления |
| № |
Y
|
X
|
Y*X
|
Y2
|
X2
|
|
1
|
10 |
14 |
140 |
100 |
196 |
|
2
|
15 |
20 |
300 |
225 |
400 |
|
3
|
6 |
6 |
36 |
36 |
36 |
|
4
|
20 |
20 |
400 |
400 |
400 |
|
5
|
9 |
10 |
90 |
81 |
100 |
|
S
|
60 |
70 |
966 |
842 |
1132 |
|
Средние
|
12
|
14
|
193,2
|
168,4
|
226,4
|
|
|
|
|
|
|
|
|
Sx2
|
30,4
|
|
|
|
|
|
Sy2
|
24,4
|
|
|
|
|
|
Sx
|
5,51
|
|
|
|
|
|
Sy
|
4,94
|
|
|
|
|
|
r
|
0,925
|
|
|
|
|
Таким
образом, коэффициент корреляции r=0,925, следовательно, можно сделать вывод, что между двумя
факторами присутствует связь прямая и очень тесная.
Ответ: данные величины
коррелируют.
По данным
таблицы сделайте прогноз значения X, если Y = 3.
| X |
4 |
2 |
3 |
7 |
5 |
6 |
3 |
| Y |
2 |
7 |
4 |
6 |
5 |
2 |
1 |
Решение:
1. Определим и оценим тесноту корреляционной зависимости
между величинами Y и X с помощью коэффициента корреляции 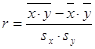 . .
|
|
|
|
Промежуточные
вычисления |
Уравнение
регрессии |
| № |
Y
|
X
|
Y*X
|
Y2
|
X2
|
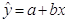
|
|
1
|
2 |
4 |
8 |
4 |
16 |
3,853 |
|
2
|
7 |
2 |
14 |
49 |
4 |
3,824 |
|
3
|
4 |
3 |
12 |
16 |
9 |
3,838 |
|
4
|
6 |
7 |
42 |
36 |
49 |
3,897 |
|
5
|
5 |
5 |
25 |
25 |
25 |
3,868 |
|
6
|
2 |
6 |
12 |
4 |
36 |
3,882 |
|
7
|
1 |
3 |
3 |
1 |
9 |
3,838 |
|
S
|
27
|
30
|
116
|
135
|
148
|
3,84
|
|
Средние
|
3,86
|
4,29
|
16,57
|
19,29
|
21,14
|
|
|
Sx
|
1,67
|
|
|
a
|
3,794
|
|
|
Sy
|
2,10
|
|
|
b
|
0,015
|
|
|
r
|
0,012
|
|
|
|
|
|
Коэффициент
корреляции r=0,012,
следовательно можно сделать вывод, что между двумя факторами связь прямая, но
очень слабая (почти отсутствует).
Уравнение
регрессии выбирают по возможности простым, и оно, как правило, лишь приближенно
описывает зависимость между значениями x одного признака и
соответствующими средними значениями другого признака 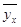 . .
Наиболее
простой и употребляемый вид зависимости – линейная зависимость. Она
определяется уравнением линейной регрессии.
В
рассматриваемом примере предположим, что эмпирическая линия регрессии
приближается к прямой, и, следовательно, теоретическая линия регрессии может
быть представлена уравнением вида: 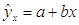 и
изображается на графике в виде прямой регрессии. Уравнение регрессии называется
выборочным, поскольку его параметры a и b находятся по
результатам выборки (хi, уi), i=1,2,… n,
причем наилучшим образом в смысле метода наименьших квадратов. Сущность метода
заключается в том, чтобы была наименьшей сумма квадратов отклонений наблюдаемых
значений уi от соответствующих значений и
изображается на графике в виде прямой регрессии. Уравнение регрессии называется
выборочным, поскольку его параметры a и b находятся по
результатам выборки (хi, уi), i=1,2,… n,
причем наилучшим образом в смысле метода наименьших квадратов. Сущность метода
заключается в том, чтобы была наименьшей сумма квадратов отклонений наблюдаемых
значений уi от соответствующих значений 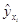 , вычисленных по уравнению
регрессии , вычисленных по уравнению
регрессии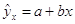 , то есть , то есть 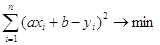
Для нахождения параметров а и b
уравнения регрессии используем метод наименьших квадратов. Для этого составим и
решим систему линейных уравнений:
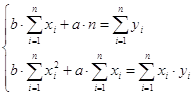 → → 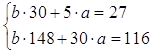
Решив систему уравнений, получим следующие
значения параметров
a=3,794.
b=0,015.
Уравнение линейной регрессии 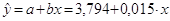 . .
Прогноз значения X, если Y = 3 при линейной зависимости
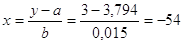
1.
Адрухаев Х.М. Сборник
задач по теории вероятностей./ Под ред. Проф. А.С. Солодовникова. – М.:
Высшая школа, 2005.
2.
Горелова Г.В. Теория
вероятностей и математическая статистика в примерах и задачах с применением MS Excel. /Под ред. Г.В. Гореловой,
И.А. Кацко. – Ростов н/Д: Феникс, 2006.
3.
Информатика
и математика для юристов. /Под ред. Проф. Х.А. Адриашина, проф. С.Я. Казанцева.
– М.: Юнити-Дана, Закон и право, 2003
4.
Ковбаса С.И.,
Ивановский В.Б. Теория вероятностей и математическая статистика:
Учебное пособие для экономистов. – СПб.: Альфа, 2001.
5.
Кремер Н.Ш. Теория
вероятностей и математическая статистика: Учебник. – М.: ЮНИТИ-ДАНА, 2007.
6.
Ниворожкина Л.И.,
Морозова З.А. Основы статистики с элементами теории вероятностей для
экономистов: Руководство для решения задач. – Ростов н/Д: Феникс, 1999 г. Информатика
7.
Пехлецкий И.Д. Математика.
/ Под ред. И.Д. Пехлецкого. – М.: Издательский центр «Академия», 2003.
8.
Пугачев В.С. Теория
вероятностей и математическая статистика: Учебное пособие. – М.: ФИЗМАТЛИТ,
2002.
9.
Сборник
задач по теории вероятностей, математической статистике и теории случайных
чисел: Учебное пособие. /Под общ. Ред. А.А. Свешникова. – СПб: Издательство
«Лань», 2007.
[1] Ранжирование – операция, заключенная в
расположении значений признака по возрастанию
|