Контрольная работа: Измерение частоты и интервалов времени
Контрольная работа: Измерение частоты и интервалов времени
Федеральное
агентство по образованию
Волгоградский
государственный технический университет
Контрольная работа
по
предмету: Метрология
на
тему: Измерение частоты и интервалов времени
Выполнила тудентка
Группы ВЗК – 282
с
Луценко Г.В.
Проверил
преподаватель
Исаев А.В.
План
1. Цифровые частотомеры
2. Измерение частоты
3. Измерение периода
4. Погрешности измерения
частоты
5. Погрешности измерения
периода
6. Повышение эффективности
обработки сигналов при оценке частотно-временных параметров
Цифровые частотомеры
Среди цифровых приборов частотно-временной
группы электронно-счетные частотомеры (в дальнейшем цифровые частотомеры - ЦЧ)
являются наиболее распространенными, что объясняется, их универсальностью,
высокими метрологическими и эксплуатационными характеристиками.
В основу построения ЦЧ положены общие принципы,
позволяющие реализовать ряд режимов работы прибора для измерения нескольких величин.
Функционально полные ЦЧ позволяют измерять следующие величины: частоту, период,
отношение двух частот (иногда выраженное в процентах), длительность импульса
или интервала времени, задаваемого пользователем; предусматриваются также режим
счета событий (импульсов) и использование ЦЧ как источника сигналов с
известными (калиброванными) частотами. Режимы работы задаются и выбираются положением
ряда переключателей (механических или электронных) и других органов управления. В более простых вариантах
исполнения ЦЧ используются для измерения меньшего числа величин (например,
одной или двух).
В любом режиме часть структуры ЦЧ остается
неизменной и в ней происходит счет числа импульсов 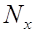 ,
пропорционального измеряемой величине. Эти импульсы проходят через электронный
ключ ЭК, находящийся в замкнутом состоянии, на счетчик импульсов СИ. Код числа,
образующийся в СИ, поступает на цифровое отсчетное устройство ЦОУ. В состав ЦОУ
входит многодекадный цифровой индикатор с перемещающейся, запятой и, как
правило, индикатор с обозначением единиц измерения. ,
пропорционального измеряемой величине. Эти импульсы проходят через электронный
ключ ЭК, находящийся в замкнутом состоянии, на счетчик импульсов СИ. Код числа,
образующийся в СИ, поступает на цифровое отсчетное устройство ЦОУ. В состав ЦОУ
входит многодекадный цифровой индикатор с перемещающейся, запятой и, как
правило, индикатор с обозначением единиц измерения.
Время замкнутого состояния ЭК, называемое
временем счета 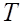 СЧ,
определяется родом измеряемой величины, а его конкретное значение рядом
соображений, о которых будет сказано ниже. СЧ,
определяется родом измеряемой величины, а его конкретное значение рядом
соображений, о которых будет сказано ниже.
Измерение частоты
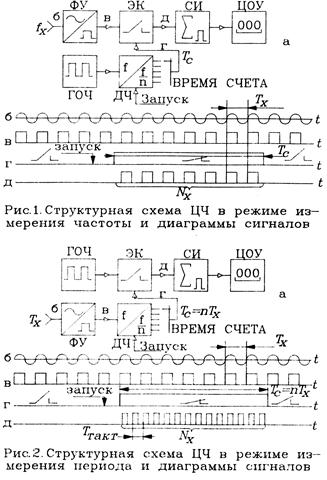
Структурная
схема ЦЧ в этом режиме работы приведена на рис.1 а. Напряжение измеряемой
частоты fx (рис.1б) подается на вход
формирующего устройства (ФУ), назначение которого - формирование сигнала
стандартной формы при достаточно произвольной форме входного сигнала. Обычно в
состав ФУ входят усилитель-ограничитель, обеспечивающий заданную амплитуду
своего выходного сигнала, и формирователь для обеспечения малой длительности
фронта и среза импульсов на выходе ФУ. Частота этих импульсов равна частоте
входного сигнала (рис. 1в). Эти импульсы проходят через ЭК на СИ в течение
времени счета Тс , которое задается генератором
опорной частоты ГОЧ и делителем частоты ДЧ. Частота ГОЧ стабилизирована
кварцевым резонатором. Необходимое Тс выбирается
переключателем ВРЕМЯ СЧЕТА. При каждом запуске прибора на выходе ДЧ появляется
один импульс (рис. 1в), под действием которого замыкается ЭК.
Число импульсов Nx, прошедшее на СИ, определяется
приближенной формулой
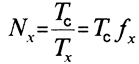
а
значение измеряемой частоты
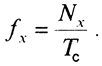
Измерение периода
Структура ЦЧ в этом
режиме приведена на рис. 2а. В этом режиме время замкнутого состояния ЭК
задается периодом (или n периодами).
Входной сигнал, период которого Tx измеряется (рис. 2б) так же, как и при измерении
частоты, подается на вход ФУ. Выходной сигнал ФУ (рис. 2в) поступает на
делитель частоты ДЧ (множитель периодов Tx). Число n (обычно n
- это 1, 10, 102,
103 или 104) выбирается переключателем ВРЕМЯ СЧЕТА, т.е.,
пТx. При запуске на выходе ДЧ появляется
импульс по длительности равный пТx (рис. 2г), в течение которого СИ подсчитывает прошедшие
за это время импульсы с известным периодом следования Tтакт (рис. 2д), называемые часто «метками
времени».
Число импульсов Nx
и период Tx, приближенно
определяются формулами (3) и (4):
Nx=nTx/Tтакт
Tx=NxTтакт/n
Известно, что частота f и период T связаны формулой l=f T.
Поэтому через прямое измерение одной из этих величин можно найти результат
косвенного измерения другой.
Погрешности измерения частоты
В режиме измерения частоты в течение Tc
подсчитываются импульсы, следующие с измеряемой частотой fx
(рис. 3а). Для этого случая имеем:
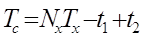 (5) (5)
Если не принимать специальных мер по синхронизации импульса Tc и импульсов измеряемой частоты (т. е., если
не задается принудительно определенное положение этих импульсов по отношению
друг к другу), то интервалы t1 и t2 являются независимыми величинами, значения
каждой из которых лежит в интервале 0 – Tx
и поэтому
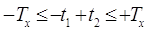
Поделив обе части уравнения (5) на произведение TcTx,
получаем
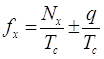 (6) (6)
с учетом, что
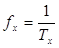 и и 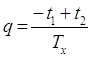 , ,  . .
В режиме измерения частоты величина 1/Tc
является ценой единицы младшего разряда счетчика (Cf=1/Tc), имеющая размерность Герц (с-1).
В зависимости от выбранного значения Tc
будем иметь Сf=1 Гц (Tc=1c), Сf=10 Гц (Tc=0,1c), Сf=0,1
Гц (Tc=10c) и
т. д. Поэтому формулу (6) можно представить в виде
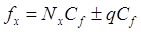
Случайную составляющую погрешности 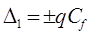 называют
погрешностью счета (при более строгом подходе в этой погрешности выделяют две
составляющие: погрешность дискретности и погрешность несинхронизации). называют
погрешностью счета (при более строгом подходе в этой погрешности выделяют две
составляющие: погрешность дискретности и погрешность несинхронизации).
Относительное значение этой погрешности равно
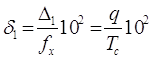 , причем , причем  . .
Другим источником погрешностей ЦЧ является отклонение Tc от номинального значения и его
нестабильность. В ЦЧ Tc формируется
из целого числа периодов колебаний кварцевого генератора, для которого
характерна чрезвычайно высокая стабильность частоты генерируемых им колебаний.
Для уменьшения влияния температуры среды в ЦЧ применяется термостатирование
генератора.
Таким образом, вторая составляющая погрешности измерения частоты
определяется нестабильностью частоты кварцевого генератора
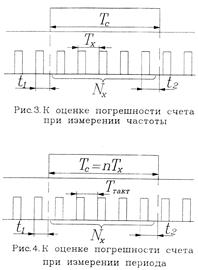
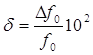 [%] и поэтому [%] и поэтому 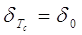 . .
Следовательно, 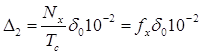 и и 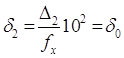 . .
Суммарные погрешности измерения частоты равны
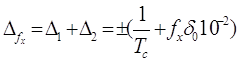 , [Гц] , [Гц]
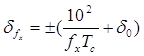 , [%] , [%]
Погрешности измерения периода. При
измерении периода (рис. 3б) в течение Tx
(или nTx) на СИ проходят импульсы с
известным периодом следования Ттакт и поэтому (см. рис. 4б)
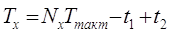 . .
Так же, как и в предыдущем случае, -t1+t2 является случайной величиной, причем,
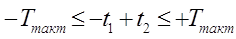 , т. е. , т. е.
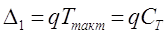 . .
При измерении n периодов имеем
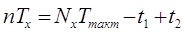 или или
 , ,
что эквивалентно уменьшению цены единицы младшего разряда в n раз.
Период следования импульсов Ттакт задается тем же
кварцевым генератором, и все предыдущие замечания в отношении нестабильности Тс
полностью справедливы и для этого режима работы. Поэтому
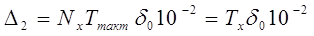 и и 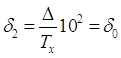
Суммарные погрешности (абсолютная и относительная) измерения периода
определяются выражениями:
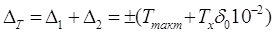 , [c] , [c]
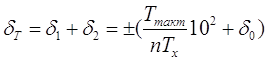 , [%] , [%]
Повышение эффективности обработки сигналов при оценке
частотно-временных параметров
Выбор и оптимизацию
алгоритмов обработки данных при оценке частотно-временных параметров
исследуемых сигналов выполняют при разработке и построении самых различных
радиотехнических систем и приборов, работающих на этих принципах. Наиболее
распространенным методом построения аппаратуры и выводы о предельных значениях
статистических оценок среднего значения частотно-временных параметров в случае
отсутствия априорных данных об исследуемом сигнале, является метод обнаружения
и оценки значений неизвестных параметров по максимуму функции правдоподобия,
который реализуется в корреляционных и многоканальных устройствах. Трудности,
связанные с реализацией таких устройств обеспечивающих потенциальные точностные
характеристики, привели к тому, что на практике нашли широкое распространение
классические одноканальные цифровые устройства обработки сигналов (цифровые
измерители среднего значения мгновенной частоты частотомеры), для которых
исследование механизма возникновения и снижения погрешностей при оценке
частотно-временных параметров является актуальной задачей исследования.
Возможности повышения эффективности обработки сигналов при оценке
частотно-временных параметров можно получить, исследуя распространенную модель
аддитивной смеси гармонического сигнала и узкополосного детерминированного или
случайного процесса:
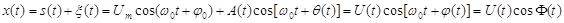 , ,
где Um,
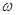 0 и 0 и 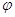 0 - амплитуда,
угловая частота и начальная фаза сигнала, а A(t) и θ(t) - огибающая и фаза случайного процесса ξ(t); U(t), 0 - амплитуда,
угловая частота и начальная фаза сигнала, а A(t) и θ(t) - огибающая и фаза случайного процесса ξ(t); U(t), 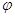 (t) и Φ(t) - огибающая, случайная фаза и полная фаза аддитивной смеси,
представляющая собой случайный нестационарный процесс. (t) и Φ(t) - огибающая, случайная фаза и полная фаза аддитивной смеси,
представляющая собой случайный нестационарный процесс.
Одной из исследуемых
функцией, представляющей практический интерес, является мгновенная частота,
связанная с полной фазой известным соотношением:
ω(t)=dΦ(t)/dt=ω0+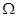 (t), (t),
где 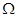 (t)= (t)=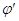 (t) - случайная частота, определяемая через производную случайной
фазы аддитивной смеси и характеризующая скорость ее изменения. (t) - случайная частота, определяемая через производную случайной
фазы аддитивной смеси и характеризующая скорость ее изменения.
Оценка математического ожидания случайного процесса 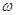 (t) на интервале
времени усреднения Т в общем виде может быть выполнена по формуле [2]: (t) на интервале
времени усреднения Т в общем виде может быть выполнена по формуле [2]:
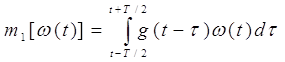 , ,
где g(t) – весовая функция оператора сглаживания,
удовлетворяющая условию несмещенности оценки:
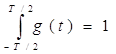
Среднее значение мгновенной частоты, вычисляемое
классическими цифровыми частотомерами, определяется по приращению полной фазы
сигнала на интервале времени усреднения T = tk - tн,
то есть используется информация о значениях полной фазы в начале Φ(tн) и конце Φ(tk) измерительного интервала с
приращением, равным:
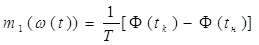
или относительно середины измерительного интервала:
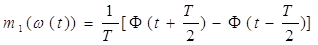
Из приведенных аналитических выражений следует, что
классический измеритель среднего значения мгновенной частоты реализует операцию
дифференцирования фазы сигнала, а (3) является дифференциально-разностным
уравнением, для которого существует интегральная форма, являющаяся оператором
текущего сглаживания:
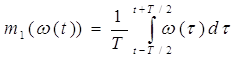
совпадающим с (1) при 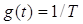 и
осуществляет выборку усредненных значений мгновенной частоты с равномерным
шагом, кратным времени измерения. и
осуществляет выборку усредненных значений мгновенной частоты с равномерным
шагом, кратным времени измерения.
Использование весовой обработки в соответствии с
выражением (1), позволяет существенно повысить точность и помехоустойчивость
устройств, работа которых основана на использовании формулы (4). Как показано в
[2], оптимизация весовой обработки позволяет получать практически потенциальные
оценки среднего значения мгновенной частоты при стационарных флуктуациях
случайной фазы исследуемого сигнала.
Эффективность весовой обработки при переходе к
цифровому измерению среднего значения мгновенной частоты снижается по сравнению
с обобщенным алгоритмом (1). При цифровых измерениях с весовой обработкой результатов
промежуточных отсчетов искомое значение среднего значения мгновенной частоты
определяется в дискретные моменты времени, а оценка среднего значения
мгновенной частоты при циклических измерениях производится с интервалом
дискретности, пропорциональным времени усреднения, то есть на выходе измерителя
формируется функция m1(ω(кT)), где к -
число циклов усреднения.
Выражение (3) для оценки среднего значения мгновенной
частоты при цифровом усреднении классическим измерителем преобразуется к виду:
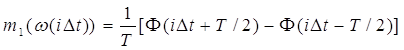 , ,
а интегральная форма (4) может быть представлена
суммой:
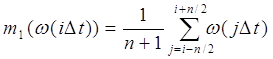 , ,
где 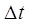 - интервал
квантования по времени, n - количество усредняемых промежуточных
временных интервалов. Оператор текущего сглаживания (1) с произвольной весовой
функцией g(t)
преобразуется в аналитическое выражение: - интервал
квантования по времени, n - количество усредняемых промежуточных
временных интервалов. Оператор текущего сглаживания (1) с произвольной весовой
функцией g(t)
преобразуется в аналитическое выражение:
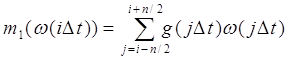
где усредненное значение результирующей оценки
мгновенной частоты на интервале времени измерения образуется суммой
промежуточных отсчетов средних значений мгновенной частоты взятых с
соответствующим весом. Усредненное значение мгновенной частоты по дискретной
выборке при этих условиях можно представить как взвешенную сумму разности
отсчетов промежуточных значений полной фазы аддитивной смеси на интервале
времени измерения:
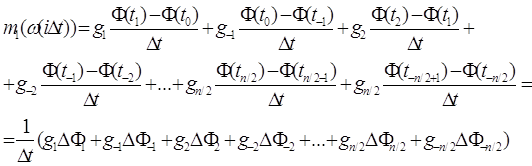
где 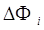 - приращение
полной фазы исследуемого сигнала на временном интервале - приращение
полной фазы исследуемого сигнала на временном интервале 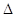 t в i-м промежуточном измерении. В соответствии с выражением
(7), усредненное значение мгновенной частоты определяется через суммирование
приращений полной фазы результирующего сигнала t в i-м промежуточном измерении. В соответствии с выражением
(7), усредненное значение мгновенной частоты определяется через суммирование
приращений полной фазы результирующего сигнала 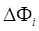
В связи с квантованием по времени возникает задача
выбора интервала квантования случайного нестационарного процесса, обеспечивающего
минимальное увеличение дисперсии оценки среднего значения мгновенной частоты
гармонического сигнала. Решение этой задачи проведем для дискретной весовой
функции Бартлетта, обладающей высокой эффективностью сглаживания флуктуационных
помех [3]. Оптимизировать интервал квантования можно как в спектральной области
на основе частотных характеристик усредняющих устройств, зависящих от
используемых весовых функций и спектральных особенностей воздействующих помех
или временным методом, исследовав погрешности оценки (7). Последнее в данном
случае представляется наиболее доступным, поэтому, учитывая условие
несмещенности оценки (2) и дискретную весовую функцию Бартлетта, определим
дисперсию оценки (7) по общим правилам для суммы зависимых случайных величин [4]:
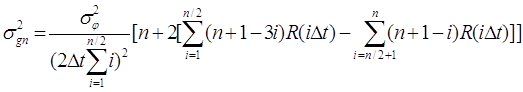
где 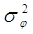 - дисперсия
фазовых флуктуаций усредняемой реализации; R(i - дисперсия
фазовых флуктуаций усредняемой реализации; R(i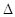 t) - значение
нормированной корреляционной функции фазовых флуктуаций, разделенных временным
интервалом t=i t) - значение
нормированной корреляционной функции фазовых флуктуаций, разделенных временным
интервалом t=i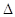 t.
После преобразований, формула (8) приводится к виду: t.
После преобразований, формула (8) приводится к виду:

а так как количество промежуточных измерений n=T/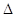 t,
то из (9) получим: t,
то из (9) получим:
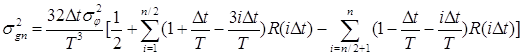
При больших n выражение (10) упрощается и,
переходя к непрерывному времени, преобразуется в интегральную форму вычисления
дисперсии оценки среднего значения мгновенной частоты:
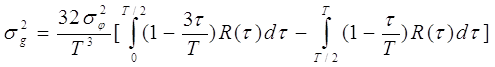
Вычислим дисперсию оценки среднего значения мгновенной
частоты на примере некоторых моделей фазовых флуктуаций, например с
экспоненциальной корреляционной функцией, нормированный вариант которой будет
иметь вид:
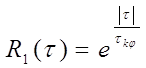
где 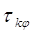 –
время корреляции фазовых флуктуаций. –
время корреляции фазовых флуктуаций.
Выполнив вычисления в соответствии с (11), в
результате получим:
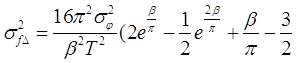
где 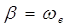 , а , а 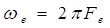 – эффективная ширина
спектра фазовых флуктуаций. – эффективная ширина
спектра фазовых флуктуаций.
При больших временах усреднения, соответствующих T
>> 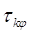 , формулы для вычисления
дисперсии (11) и (13) преобразуются к упрощенному выражению для вычисления
дисперсии оценки среднего значения мгновенной частоты: , формулы для вычисления
дисперсии (11) и (13) преобразуются к упрощенному выражению для вычисления
дисперсии оценки среднего значения мгновенной частоты:
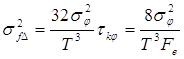
которая по сравнению с оценкой классического
измерителя, равной 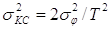 дает выигрыш в
точности, равный: дает выигрыш в
точности, равный:
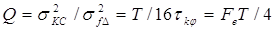
который можно достигнуть, оптимизировав обработку
исследуемого сигнала.
Полученные выражения для вычисления дисперсии оценки
среднего значения мгновенной частоты, могут быть использованы для определения
оптимального количества выборок на интервале усреднения и шага квантования по
времени. Оптимальный шаг квантования определим, составив и исследовав отношение
дисперсий (10) и (14), равное:
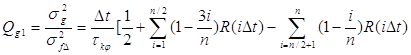
где 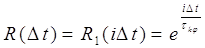 дискретный
аналог корреляционной функции (12), или для сравнения – модель фазовых
флуктуаций с равномерным энергетическим спектром и дискретный
аналог корреляционной функции (12), или для сравнения – модель фазовых
флуктуаций с равномерным энергетическим спектром и
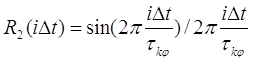
Другим выражением, представляющим интерес для
исследований, является отношение дисперсии оценки среднего значения мгновенной
частоты цифрового измерителя с весовой обработкой и дисперсии оценки среднего
значения мгновенной частоты классического измерителя, равное:
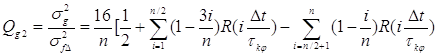
Список используемой литературы
1. Электрические измерения / Байда Л.
И., Добротворский Н. С., Душин Е. М. и др.: Под ред. А. В. Фремке и Е. М.
Душина.—Л.: Энергия, 1980.—392с.
2. Кушнир Ф. В. Электрорадиоизмерения:
Учебное пособие для вузов,— Л.: Энергоатомиэдат, 1983.—320 с.
3. Кончаловский
В.Ю., Семенов В.Ф., Солодов Ю.С. Измерение частоты и интервалов времени. - М.:
Изд-во МЭИ, 1999. -12 с.
4. Тихонов
В.И. Оптимальный прием сигналов. М.: Радио и связь, 1983, 320 с.
5. Гутников
В.С. Фильтрация измерительных сигналов. Л.: Энергоатомиздат, 1990, 192 с.
|